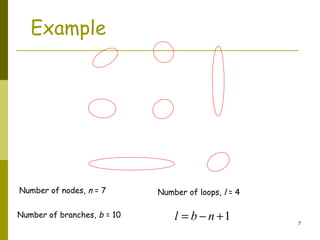
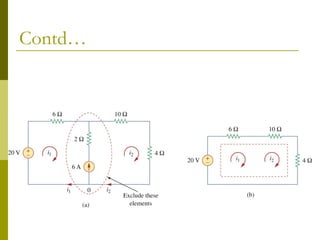
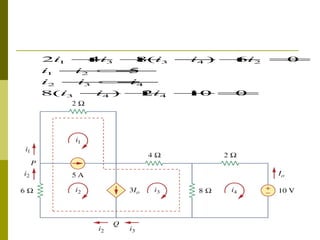
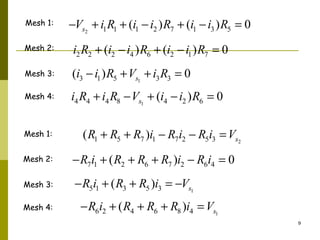This document discusses two methods for circuit analysis: mesh analysis and supermesh analysis. Mesh analysis involves identifying each loop or "mesh" in the circuit and assigning a mesh current to each one. Kirchhoff's voltage law is applied to write an equation for each mesh. Supermesh analysis combines meshes that share a current source into a single "supermesh". This reduces the number of mesh equations but introduces additional equations for the current sources. The document provides examples of setting up and solving systems of equations using both mesh and supermesh analysis.

1. MESH AND SUPERMESH
ANALYSIS
1

2. Methods of Analysis
1. Mesh Analysis
2. Supermesh Analysis

3. Process of Mesh Analysis
1. Identify every mesh in the circuit.
2. Label each mesh with a mesh current.
It is recommended that all mesh
currents be labeled in the same direction
(either clockwise (CW) or counter-clockwise
(CCW)).

4. Mesh Analysis (Cont’d)
4. Within a particular mesh of interest, use
Ohm’s law to express the voltage across
any element within that mesh as the
difference between the two mesh
currents of continuous meshes shared by
the element times the element impedance.
The current within the mesh of interest is
always considered to be larger than the
rest of the mesh currents.

5. Mesh Analysis (Cont’d)
5. Apply KVL to sum all voltages in that
mesh of interest. The resulting algebraic
equation (called mesh equation) has all
mesh currents as its unknowns.
6. Repeat steps 4 and 5 until all meshes are
accounted for. The number of equations
must be equal to the number of mesh
currents.

6. Mesh Analysis (Cont’d)
8. If a current source exists only in one
mesh, the mesh current is equal to the
source current, and KVL is not applied to
this mesh.
9. Solve the resulting simultaneous mesh
equations to obtain the values of the
unknown mesh currents.
10. Use the values of mesh currents above
to find voltages and/or currents
throughout the rest of the circuit.

7. 7
Example
Number of nodes, n = 7
Number of branches, b = 10
Number of loops, l = 4
l = b - n +1

8. 8
Example
Apply KVL to each mesh
-Vs2 + v1 + v7 - v5 = 0
2 6 7 v - v - v = 0
5 1 3 0 s v + v + v =
Mesh 1:
Mesh 2:
Mesh 3:
4 8 1 6 0 s Mesh 4: v + v -V + v =

9. 9
2 1 1 1 -Vs + i R + (i - i2 )R7 + (i1 -i3 )R5 = 0
2 2 2 4 6 2 1 7 i R + (i -i )R + (i -i )R = 0
3 1 5 1 3 3 ( ) 0 s i - i R +V + i R =
Mesh 1:
Mesh 2:
Mesh 3:
4 4 4 8 1 4 2 6 ( ) 0 s Mesh 4: i R + i R -V + i -i R =
Mesh 1:
Mesh 2:
Mesh 3:
Mesh 4:
1 5 7 1 7 2 5 3 2 ( ) s R + R + R i - R i - R i =V
7 1 2 6 7 2 6 4 -R i + (R + R + R )i - R i = 0
5 1 3 5 3 1 ( ) s -R i + R + R i = -V
6 2 4 6 8 4 1 ( ) s -R i + R + R + R i =V

10. æ + + - - öæ ö æ ö
ç ¸ç ¸ ç ¸ ç - + + - ¸ç ¸ ç ¸ = ç ¸ ç - + ¸ç ¸ - ç ¸ç ¸ ç ¸ è - + + øè ø çè ø¸
10
Mesh 1:
Mesh 2:
Mesh 3:
Mesh 4:
1 5 7 1 7 2 5 3 2 ( ) s R + R + R i - R i - R i =V
7 1 2 6 7 2 6 4 -R i + (R + R + R )i - R i = 0
5 1 3 5 3 1 ( ) s -R i + R + R i = -V
6 2 4 6 8 4 1 ( ) s -R i + R + R + R i =V
2
1
0 0
1
0
1 5 7 7 5 1
7 2 6 7 6 2
0 0
5 3 5 3
0 0
6 4 6 8 4
s
s
s
R R R R R i V
R R R R R i
R R R i V
R R R R i V

11. Supermesh
If a current source exists between two
contiguous meshes, the two meshes are
collapsed into a single mesh called a
supermesh, and the current source and any
elements connected in series with it removed.
However, KVL must still be satisfied within a
supermesh using the old mesh current labels.
Also, the removal of the current source
provides another mesh equation.

12. Contd…

13. Properties of a Supermesh
1. The current is not completely ignored
 provides the constraint equation necessary to
solve for the mesh current.
1. Several current sources in adjacency form a
bigger supermesh.

14. i i
+ =
i i
6 14 20
1 2
- = -
6
1 2
Example
If a supermesh consists of two
meshes, two equations are needed;
one is obtained using KVL and Ohm’s
law to the supermesh and the other
is obtained by relation regulated
due to the current source.

15.  Similarly, a supermesh formed from three
meshes needs three equations: one is from
the supermesh and the other two equations
are obtained from the two current sources.

16. i i i i i
++ -+=
2 4 8( ) 6 0
1 3 3 4 2
i i
-=-
5
1 2
i i i
-=-
2 3 4
i i i
-++=
8( ) 2 10 0
3 4 4

17. THANK YOU