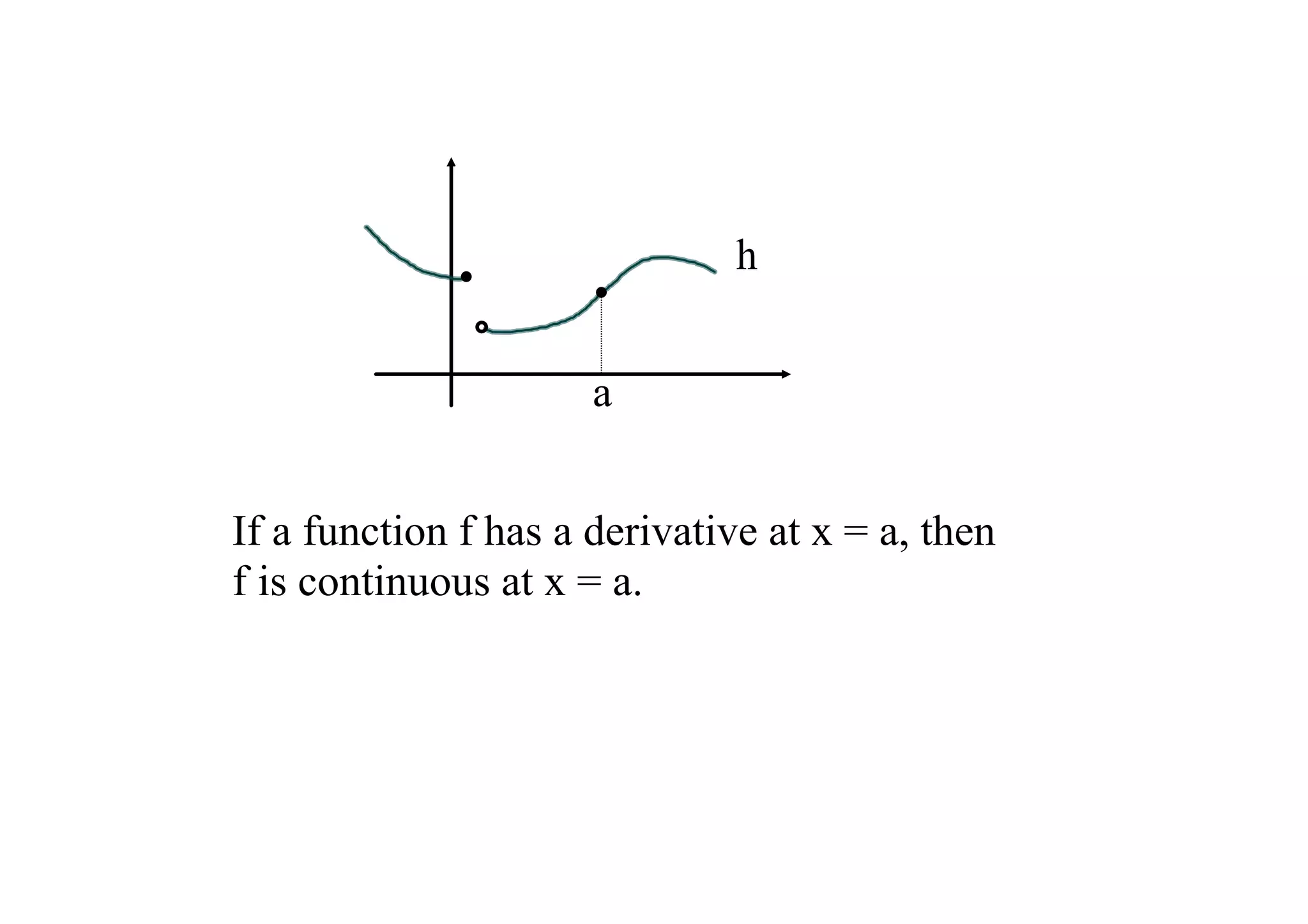
This document discusses continuity of functions, including definitions of continuity at a point and on an interval. It introduces the intermediate value theorem and extreme value theorem for continuous functions on closed intervals. It also states that differentiability at a point implies continuity at that point.

1. Continuity

2. Graph the function: x(x ­ 1)
f(x) =
(x ­ 1)

3. Graph the function: g(x) = x + 1
x ­ 1

4. A function f is continuous at x = a if:
1) lim f(x) exists
x a
2) f is defined at a
3) lim
x a
f(x) = f(a)

5. Determine if the function f defined by:
{
f(x) =
x2 ­ 4 , x = 2
x ­ 2
4 , x = 2
is continuous.

7. {
f(x) =
3 ­ x , x > 1
x2 + 2x , x < 1
Is this function continuous at x = 1?

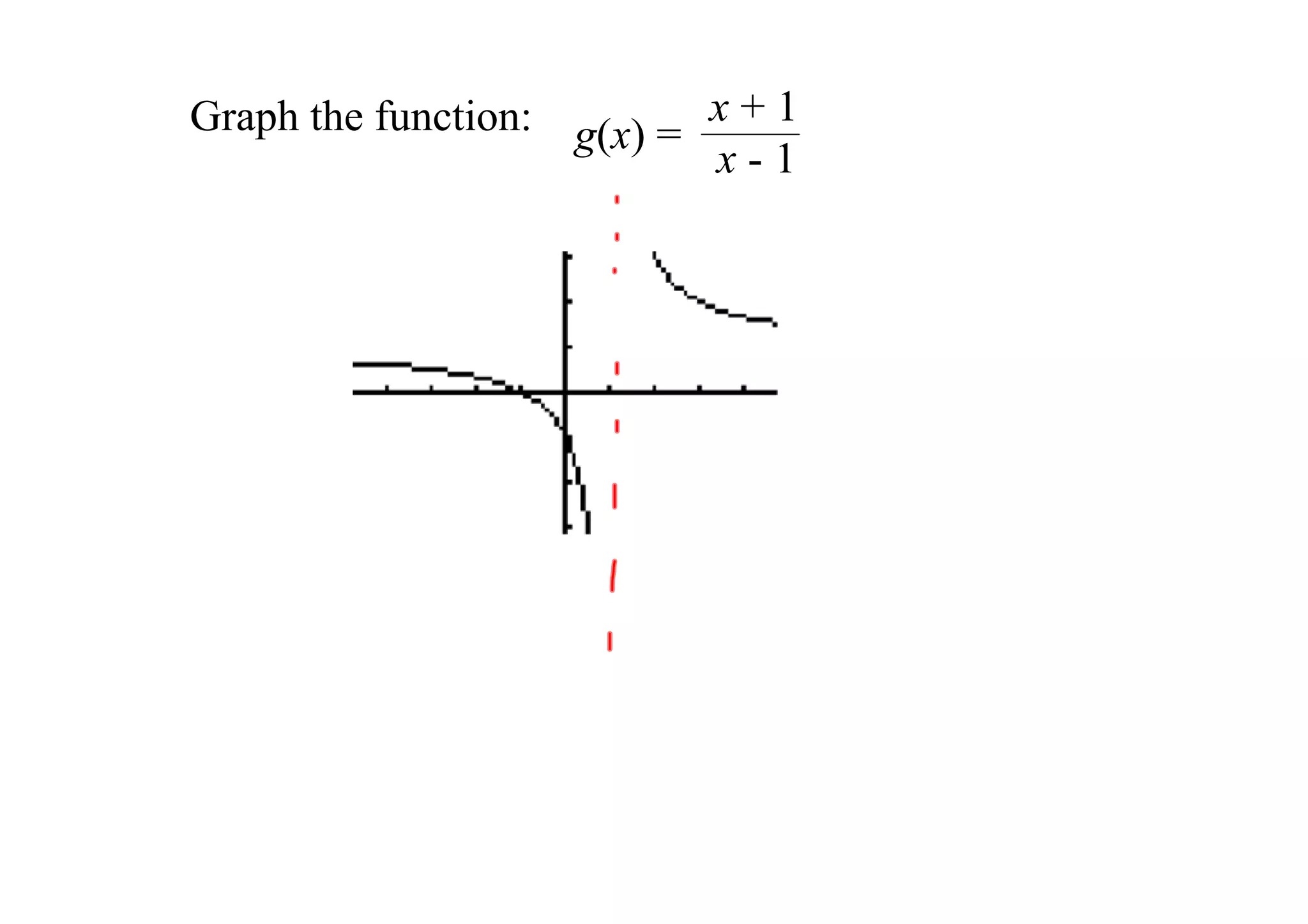
9. Continuity on an interval
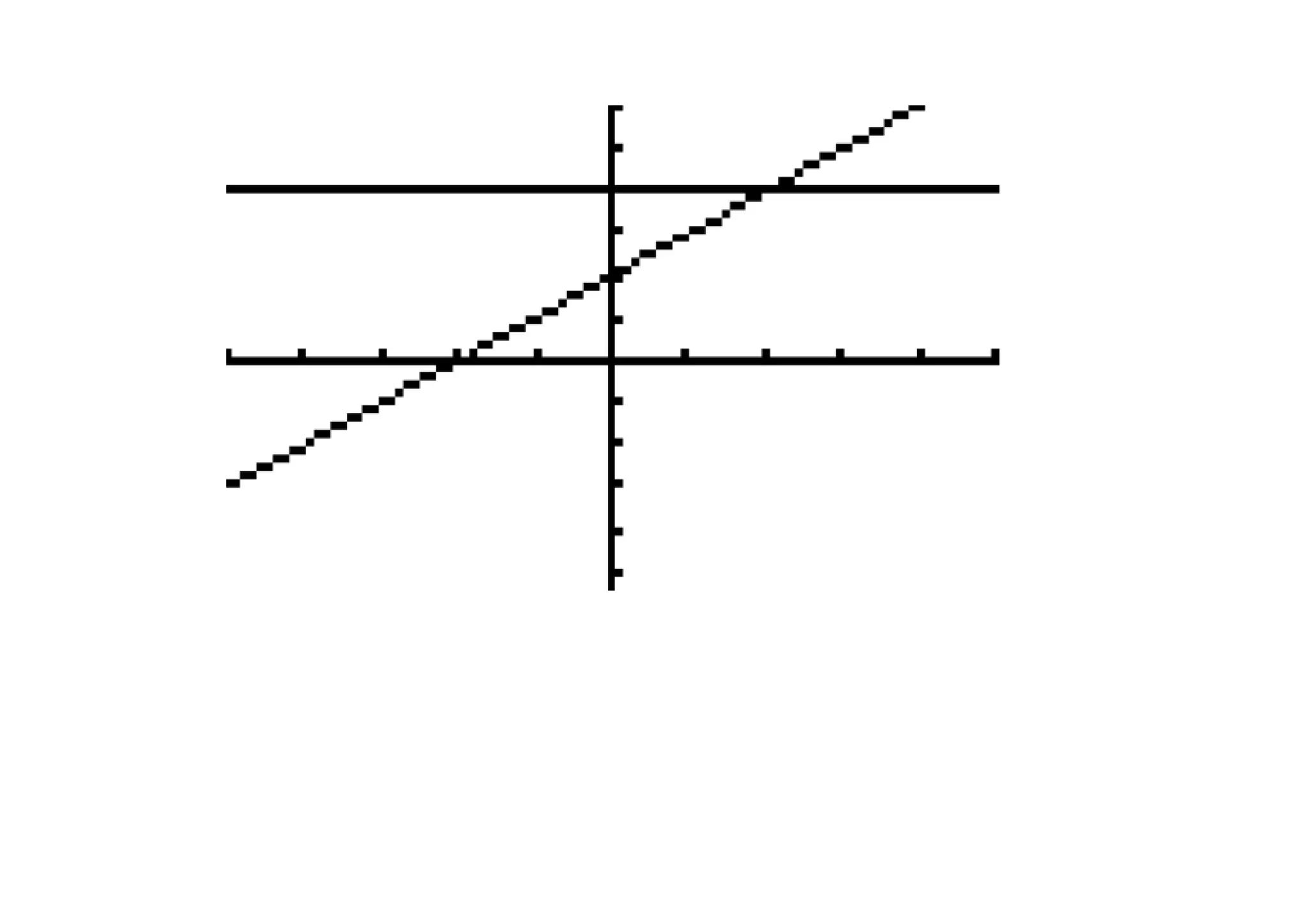
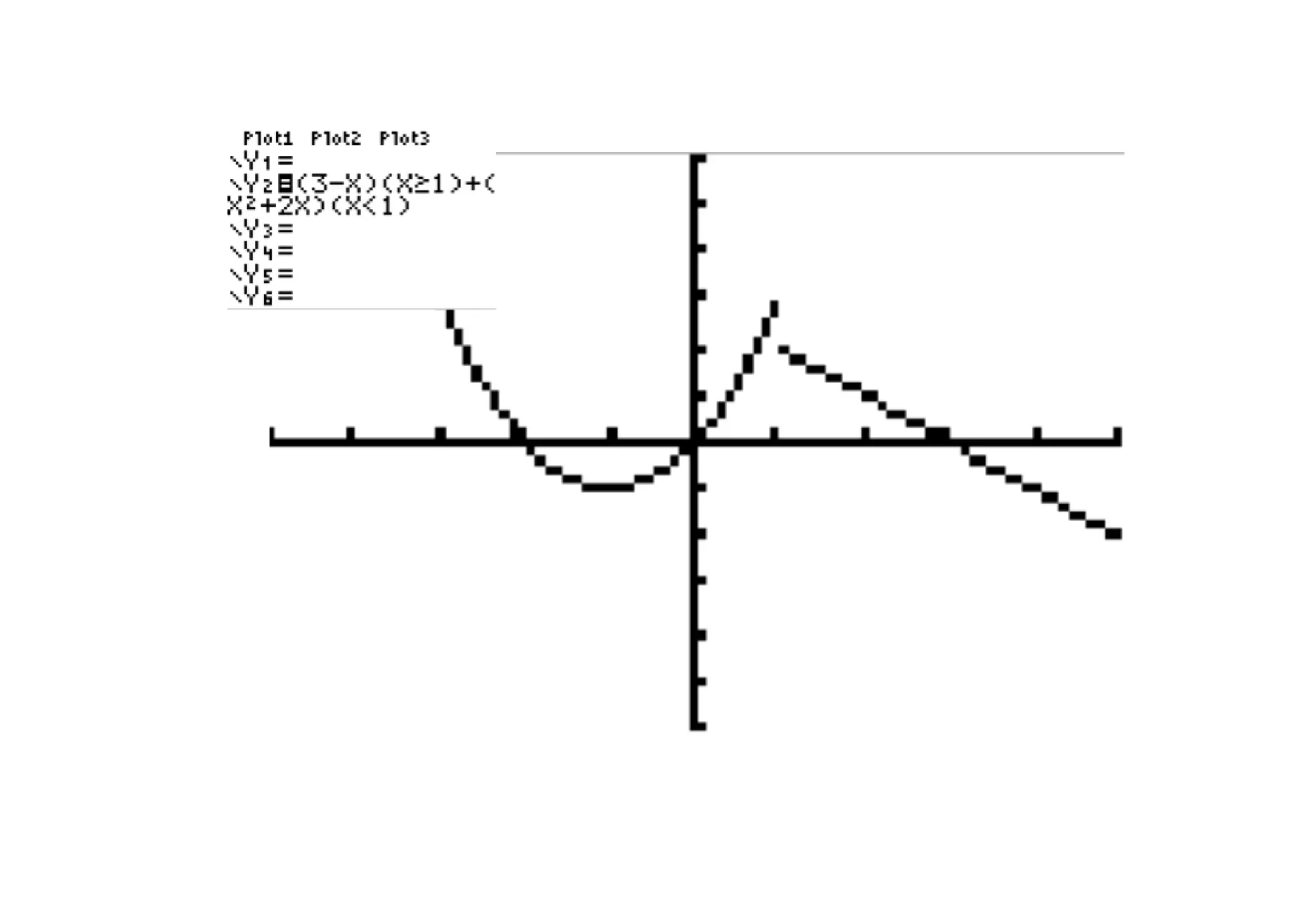
A function f is continuous on the closed interval
[a, b] if it is continuous at every number in the
open interval (a, b) and
lim
x a+
f(x) = f (a) and lim f(x) = f(b)
x b­
right continuous
left continuous

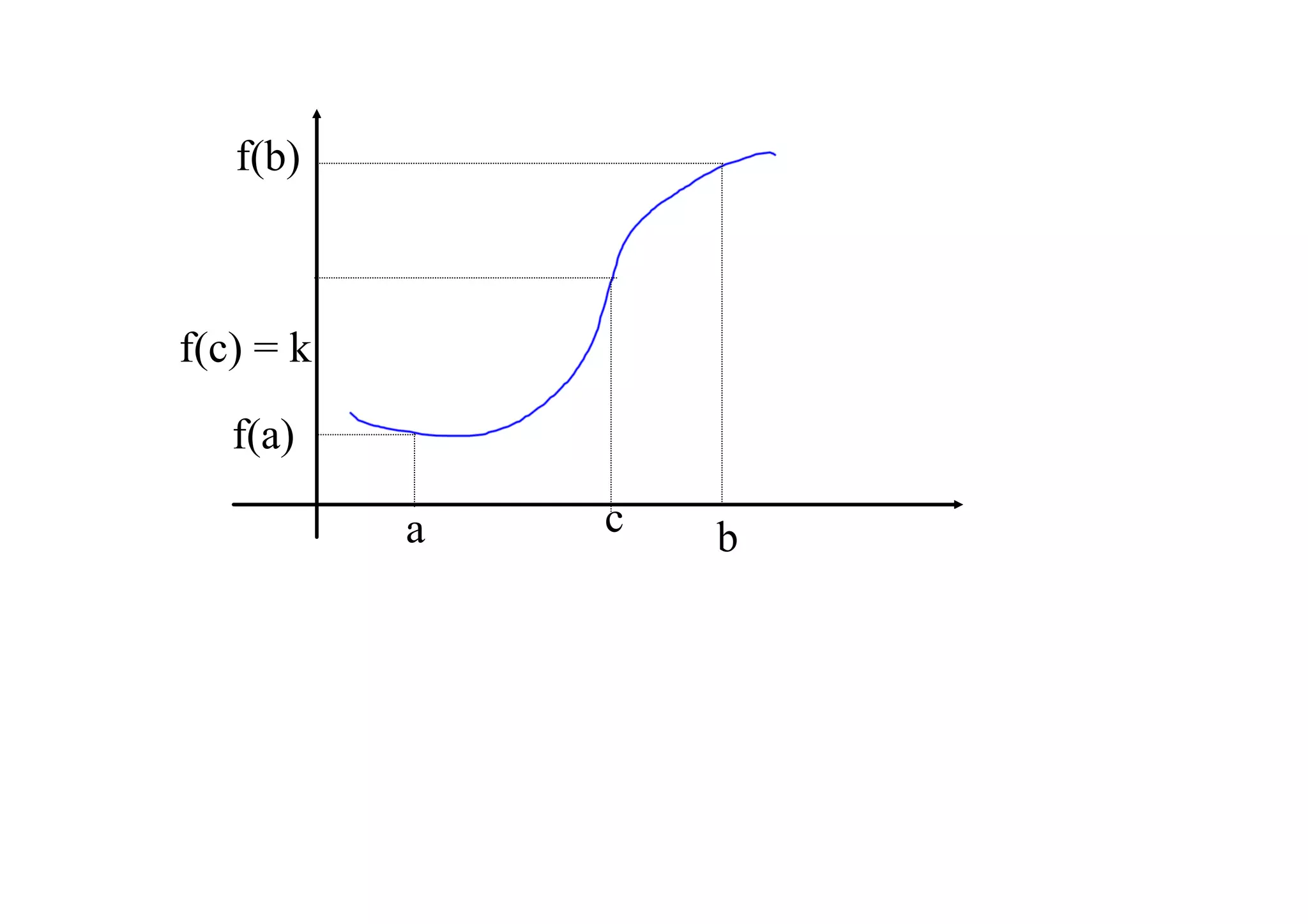
10. The Intermediate Value Theorem: If the
function f is continuous on the closed interval
[a, b], with f(a) f(b), and k is a number
=
between f(a) and f(b), then there exists at least
one number c in (a, b) for which f(c) = k.

11. f(b)
f(c) = k
f(a)
a c b

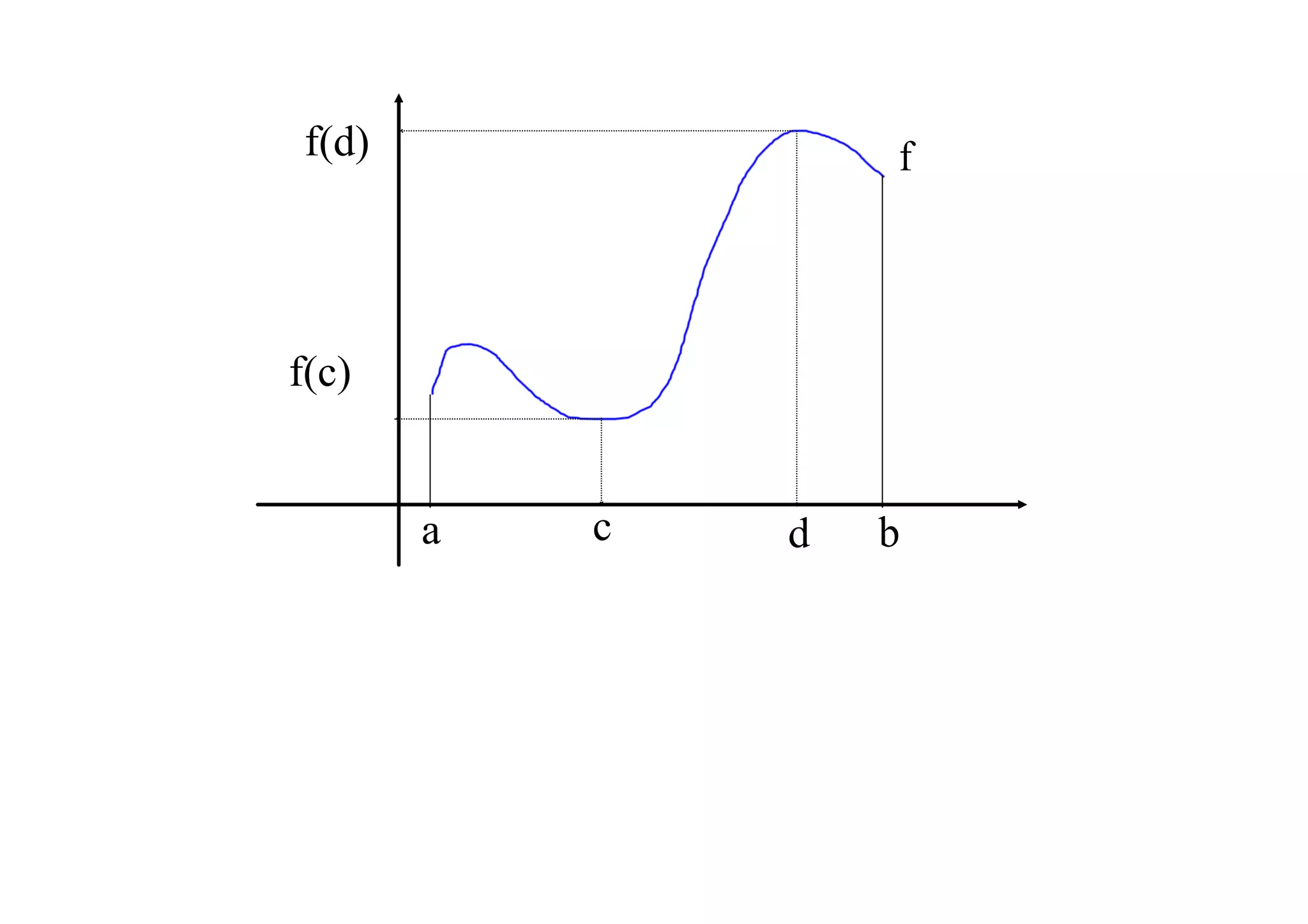
12. The Extreme Value Theorem: If the
function f is continuous on the interval [a, b],
then there exist numbers c and d in [a, b] such
that for all x in [a, b],
f(c) < f(x) and f(d) > f(x)

13. f(d) f
f(c)
a c d b

14. f
g
a
a

15. h
a
If a function f has a derivative at x = a, then
f is continuous at x = a.

16. Exercise 2.8
Questions: 1, 5, 7, 13, 15, 21