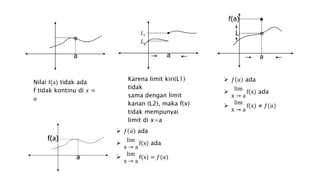
1) The document discusses the continuity of functions at a point and over an interval. 2) A function f is defined to be continuous at a point c if the limit of f(x) as x approaches c exists and is equal to f(c). 3) For a function to be continuous over an interval (a,b), it must be continuous at every point c within the interval.

1. MATEMATIKA DASAR ASWAR AMIRUDDIN, ST.,
MT.

2. PERTEMUAN 7
 Kekontinuan fungsi
 Kontinu kiri dan kontinu kanan

3. FUNGSI KONTINU DI SUATU
TITIK
Misalkan f terdefinisi
disekitar c, termasuk di c.
Fungsi f dikatakan kontinu
di c apabila
lim
x → c
𝑓(𝑥) = 𝑓(𝑐)
yakni: untuk setiap ε > 0
terdapat δ > 0 sehingga:
jika |x – c|< δ, maka|f(x) –
f(c)|< ε.
Fungsi f dikatakan kontinu
pada (a,b) apabila f
kontinu di setiap titik c є
(a,b).

4. FUNGSI KONTINU DI SUATU
TITIK
Definisi Fungsi f dikatakan kontinu di c apabila
lim
x → c
𝑓(𝑥) = 𝑓 𝑐
Jika diperuhi ketiga syarat berikut :
1. lim
x → c
f(x) ada
2. Nilai f c ada
3. lim
x → c
f(x) = f c
Jika paling kurang salah satu syarat diatas tidak dipenuhi maka f
dikatakan tidak kontinu di x=a

5. Nilai f(a) tidak ada
f tidak kontinu di 𝑥 =
𝑎
Karena limit kiri(L1)
tidak
sama dengan limit
kanan (L2), maka f(x)
tidak mempunyai
limit di x=a
 𝑓 𝑎 ada

lim
x → a
f(x) ada

lim
x → a
f(x) ≠ 𝑓(𝑎)
 𝑓 𝑎 ada

lim
x → a
f(x) ada

lim
x → a
f(x) = 𝑓(𝑎)

6. FUNGSI KONTINU DI SUATU
TITIK

7. FUNGSI KONTINU DI SUATU
TITIK

8. Contoh soal :
𝑓 𝑥 =
𝑥2−4
𝑥−2
4
Apakah f kontinu di x = 2 ?
Jawab :
1.
lim
x → 2
𝑥2−4
𝑥−2
=
lim
x → 2
(𝑥−2)(𝑥+2)
(𝑥−2)
=
lim
x → 2
𝑥 + 2 = 4
2. 𝑓 2 = 4
3.
lim
x → 2
𝑥2−4
𝑥−2
= 𝑓(2) , maka 𝑓 kontinu di x = 2.
FUNGSI KONTINU DI SUATU
TITIK
, 𝑥 ≠ 2
, 𝑥 = 2

10. Teorema 2.7.1
1. Fungsi polinom (fungsi suku banyak) kontinu pada R.
2. Jika fungsi-fungsi f dan g keduanya kontinu di c dan k
sembarang konstanta maka fungsi f + g, f – g, kf , f/g
(asal lim g(x) ≠ 0) juga kontinu di c.
3. Jika g fungsi yang kontinu di c dan f fungsi kontinu di
g(c) maka f o g kontinu di c.
FUNGSI KONTINU

11. FUNGSI KONTINU

12. FUNGSI KONTINU