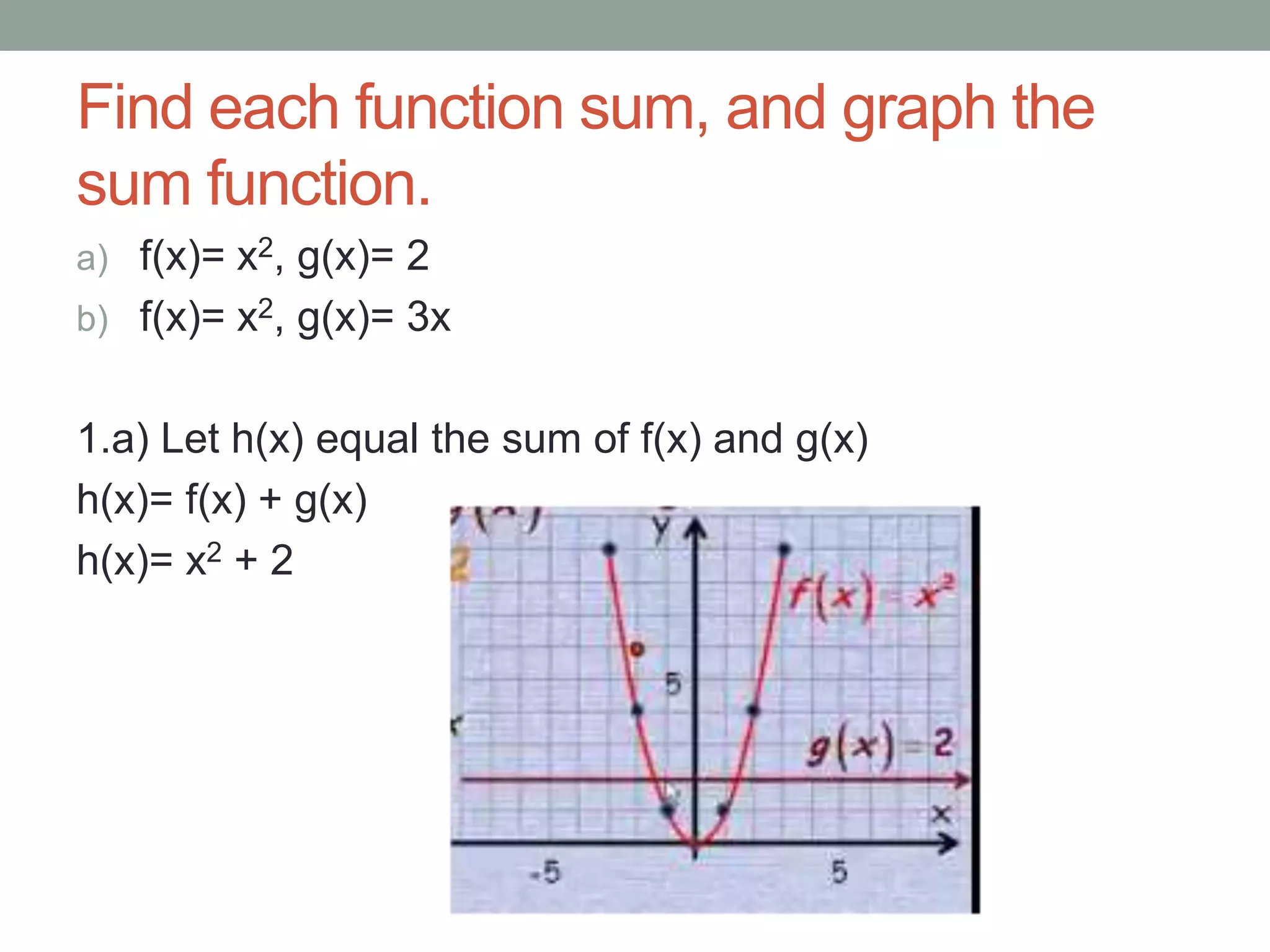
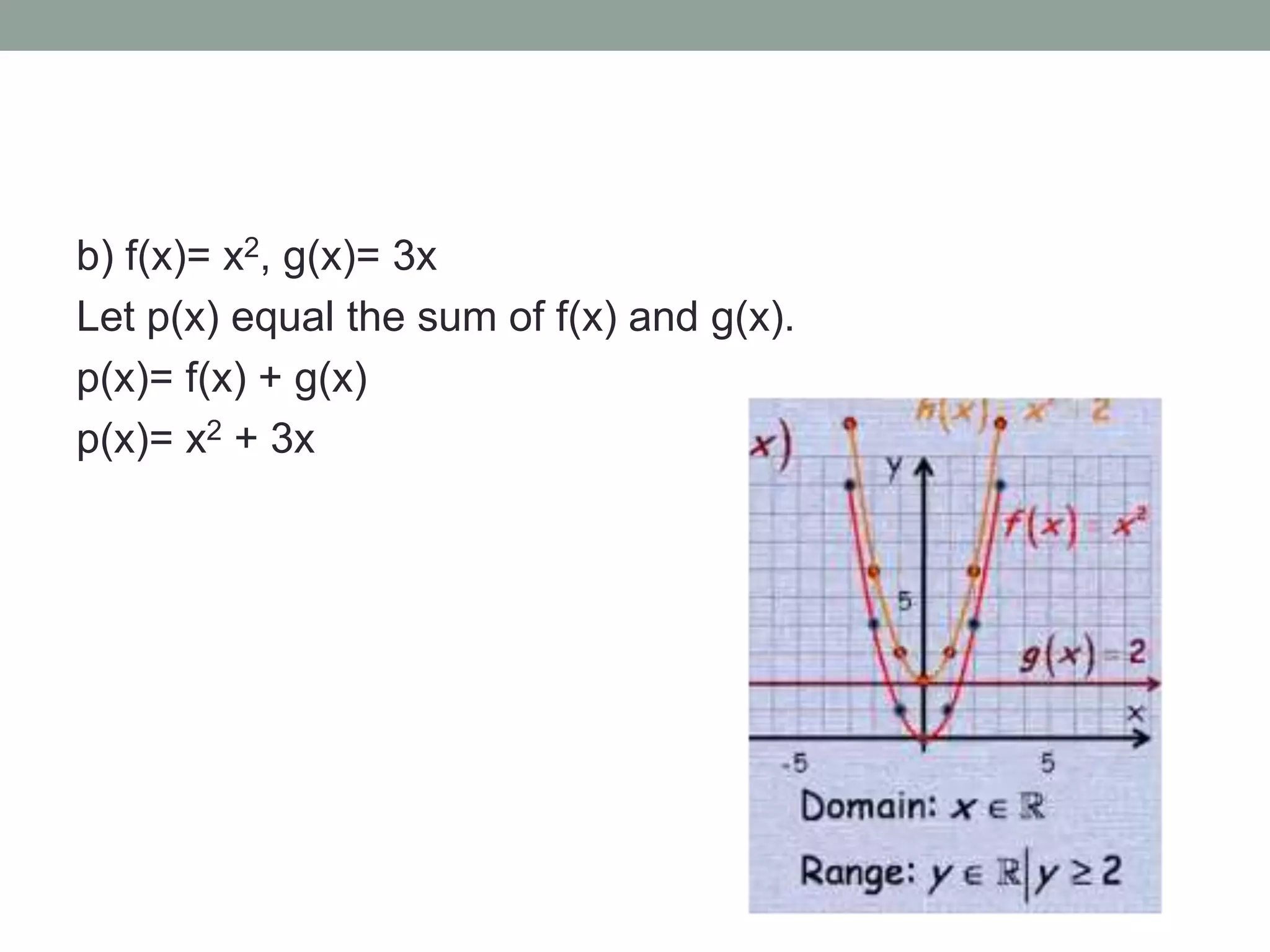
The document discusses finding the sum of two functions f(x) and g(x). It provides two examples: 1) f(x)=x^2 and g(x)=2. The sum function h(x)=x^2+2 is graphed by adding the y-values. 2) f(x)=x^2 and g(x)=3x. The sum function p(x)=x^2+3x is graphed by adding the y-values. The domain is all real numbers and the range is all real numbers greater than -9/4, as determined by finding the midpoint of the function.

1. SUMS AND DIFFERENCES
OF FUNCTIONS
Example:

2. Find each function sum, and graph the
sum function.
a) f(x)= x2, g(x)= 2
b) f(x)= x2, g(x)= 3x
1.a) Let h(x) equal the sum of f(x) and g(x)
h(x)= f(x) + g(x)
h(x)= x2 + 2

3. To get the coordinates for h(x), add the y-points together.
At -3, 2+9 = 11 Therefore (-3,11)
At -2, 2+2 = 4 Therefore (-2,4)
At -1, 2+1 = 3 Therefore (-1,3)
At 0, 0+2 = 2 Therefore (0,2)
At 1, 1+2 = 3 Therefore (1,3)
At 2, 2+2 = 4 Therefore (2,4)
At 3, 2+9 = 11 Therefore (3,11)

4. b) f(x)= x2, g(x)= 3x
Let p(x) equal the sum of f(x) and g(x).
p(x)= f(x) + g(x)
p(x)= x2 + 3x

5. To get the coordinates for p(x), add the y-points.
At -3, 9+(-9) = 0 Therefore (-3,)
At -2, 4+(-6) = -2 Therefore (-2,-2)
At -1, 1+(-3) = -2 Therefore (-1,-2)
At 0, 0+0 = 0 Therefore (0,0)
At 1, 1+3 = 4 Therefore (1,4)
At 2, 4+6 = 10 Therefore (2,10)

6. To find domain and range, you have to find the midpoint.
Midpoint:
p(x)= x2 + 3x Factor
p(x)= x(x+3)
x=0 x+3=0
x= -3
Therefore x = 0, -3

7. To find the midpoint, add the x-intercepts and divide by 2.
Midpoint = 0 + (-3)
2
= -3
2
Substitute this value into the formula to find the y
coordinate.
p(-3/2) = (-3/2)2 + 3(-3/2)
= -9/4

8. Therefore D= {XER}
R= {YER, y > -9/4}