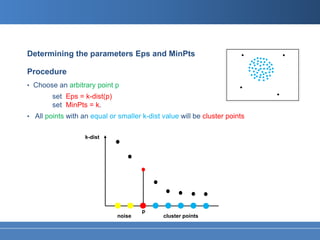
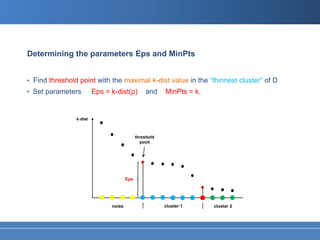
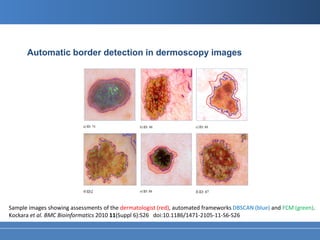
This document summarizes the DBSCAN clustering algorithm. DBSCAN finds clusters based on density, requiring only two parameters: Eps, which defines the neighborhood distance, and MinPts, the minimum number of points required to form a cluster. It can discover clusters of arbitrary shape. The algorithm works by expanding clusters from core points, which have at least MinPts points within their Eps-neighborhood. Points that are not part of any cluster are classified as noise. Applications include spatial data analysis, image segmentation, and automatic border detection in medical images.

1. Summer School
“Achievements and Applications of Contemporary Informatics,
Mathematics and Physics” (AACIMP 2011)
August 8-20, 2011, Kiev, Ukraine
Density Based Clustering
Erik Kropat
University of the Bundeswehr Munich
Institute for Theoretical Computer Science,
Mathematics and Operations Research
Neubiberg, Germany

2. DBSCAN
Density based spatial clustering of applications with noise
noise
arbitrarily shaped clusters

3. DBSCAN
DBSCAN is one of the most cited clustering algorithms in the literature.
Features
− Spatial data
geomarketing, tomography, satellite images
− Discovery of clusters with arbitrary shape
spherical, drawn-out, linear, elongated
− Good efficiency on large databases
parallel programming
− Only two parameters required
− No prior knowledge of the number of clusters required.

4. DBSCAN
Idea
− Clusters have a high density of points.
− In the area of noise the density is lower
than the density in any of the clusters.
Goal
− Formalize the notions of clusters and noise.

5. DBSCAN
Naïve approach
For each point in a cluster there are at least a minimum number (MinPts)
of points in an Eps-neighborhood of that point.
cluster

6. Neighborhood of a Point
Eps-neighborhood of a point p
NEps(p) = { q ∈ D | dist (p, q) ≤ Eps }
Eps
p

7. DBSCAN ‒ Data
Problem
• In each cluster there are two kinds of points:
cluster
̶ points inside the cluster (core points)
̶ points on the border (border points)
An Eps-neighborhood of a border point contains significantly less points than
an Eps-neighborhood of a core point.

8. Better idea
For every point p in a cluster C there is a point q ∈ C,
so that
(1) p is inside of the Eps-neighborhood of q border points are connected to core points
and
(2) NEps(q) contains at least MinPts points. core points = high density
p
q

9. Definition
A point p is directly density-reachable from a point q
with regard to the parameters Eps and MinPts, if
1) p ∈ NEps(q) (reachability)
2) | NEps(q) | ≥ MinPts (core point condition)
p
MinPts = 5
q
| NEps(q) | = 6 ≥ 5 = MinPts (core point condition)

10. Remark
Directly density-reachable is symmetric for pairs of core points.
It is not symmetric if one core point and one border point are involved.
Parameter: MinPts = 5
p p directly density reachable from q
p ∈ NEps(q)
q
| NEps(q) | = 6 ≥ 5 = MinPts (core point condition)
q not directly density reachable from p
| NEps (p) | = 4 < 5 = MinPts (core point condition)

11. Definition
A point p is density-reachable from a point q
with regard to the parameters Eps and MinPts
if there is a chain of points p1, p2, . . . ,ps with p1 = q and ps = p
such that pi+1 is directly density-reachable from pi for all 1 < i < s-1.
p
p1 MinPts = 5
| NEps(q) | = 5 = MinPts (core point condition)
q
| NEps(p1) | = 6 ≥ 5 = MinPts (core point condition)

12. Definition (density-connected)
A point p is density-connected to a point q
with regard to the parameters Eps and MinPts
if there is a point v such that both p and q are density-reachable from v.
p
MinPts = 5
v
q
Remark: Density-connectivity is a symmetric relation.

13. Definition (cluster)
A cluster with regard to the parameters Eps and MinPts
is a non-empty subset C of the database D with
1) For all p, q ∈ D: (Maximality)
If p ∈ C and q is density-reachable from p
with regard to the parameters Eps and MinPts,
then q ∈ C.
2) For all p, q ∈ C: (Connectivity)
The point p is density-connected to q
with regard to the parameters Eps and MinPts.

14. Definition (noise)
Let C1,...,Ck be the clusters of the database D
with regard to the parameters Eps i and MinPts I (i=1,...,k).
The set of points in the database D not belonging to any cluster C1,...,Ck
is called noise:
Noise = { p ∈ D | p ∉ Ci for all i = 1,...,k}
noise

15. Two-Step Approach
If the parameters Eps and MinPts are given,
a cluster can be discovered in a two-step approach:
1) Choose an arbitrary point v from the database
satisfying the core point condition as a seed.
2) Retrieve all points that are density-reachable from the seed
obtaining the cluster containing the seed.

16. DBSCAN (algorithm)
(1) Start with an arbitrary point p from the database and
retrieve all points density-reachable from p
with regard to Eps and MinPts.
(2) If p is a core point, the procedure yields a cluster
with regard to Eps and MinPts
and the point is classified.
(3) If p is a border point, no points are density-reachable from p
and DBSCAN visits the next unclassified point in the database.

17. Algorithm: DBSCAN
INPUT: Database SetOfPoints, Eps, MinPts
OUTPUT: Clusters, region of noise
(1) ClusterID := nextID(NOISE);
(2) Foreach p ∈ SetOfPoints do
(3) if p.classifiedAs == UNCLASSIFIED then
(4) if ExpandCluster(SetOfPoints, p, ClusterID, Eps, MinPts) then
(5) ClusterID++;
(6) endif
(7) endif
(8) endforeach
SetOfPoints = the database or a discovered cluster from a previous run.

18. Function: ExpandCluster
INPUT: SetOfPoints, p, ClusterID, Eps, MinPts
OUTPUT: True, if p is a core point; False, else.
(1) seeds = NEps(p);
(2) if seeds.size < MinPts then // no core point
(3) p.classifiedAs = NOISE;
(4) return FALSE;
(5) else // all points in seeds are density-reachable from p
(6) foreach q ∈ seeds do
(7) q.classifiedAs = ClusterID
(8) endforeach

19. Function: ExpandCluster (continued)
(9) seeds = seeds {p};
(10) while seeds ≠ ∅ do
(11) currentP = seeds.first();
(12) result = NEps(currentP);
(13) if result.size ≥ MinPts then
(14) foreach resultP ∈ result and
resultP.classifiedAs ∈ {UNCLASSIFIED, NOISE} do
(15) if resultP.classifiedAs == UNCLASSIFIED then
(16) seeds = seeds ∪ {resultP};
(17) endif
(18) resultP.classifiedAs = ClusterID;
(19) endforeach
(20) endif
(21) seeds = seeds {currentP};
(22) endwhile
(23) return TRUE;
(24) endif
Source: A. Naprienko: Dichtebasierte Verfahren der Clusteranalyse raumbezogener Daten am Beispiel von DBSCAN und Fuzzy-DBSCAN.
Universität der Bundeswehr München, student’s project, WT2011.

20. Density Based Clustering
‒ The Parameters Eps and MinPts ‒

21. Determining the parameters Eps and MinPts
The parameters Eps and MinPts can be determined by a heuristic.
Observation
• For points in a cluster, their k-th nearest neighbors are at roughly the same distance.
• Noise points have the k-th nearest neighbor at farther distance.
⇒ Plot sorted distance of every point to its k-th nearest neighbor.

22. Determining the parameters Eps and MinPts
Procedure
• Define a function k-dist from the database to the real numbers,
mapping each point to the distance from its k-th nearest neighbor.
• Sort the points of the database in descending order of their k-dist values.
k-dist
database

23. Determining the parameters Eps and MinPts
Procedure
• Choose an arbitrary point p
set Eps = k-dist(p)
set MinPts = k.
• All points with an equal or smaller k-dist value will be cluster points
k-dist
p
noise cluster points

24. Determining the parameters Eps and MinPts
Idea: Use the point density of the least dense cluster in the data set as parameters

25. Determining the parameters Eps and MinPts
• Find threshold point with the maximal k-dist value in the “thinnest cluster” of D
• Set parameters Eps = k-dist(p) and MinPts = k.
Eps
noise cluster 1 cluster 2

26. Density Based Clustering
‒ Applications ‒

27. Automatic border detection in dermoscopy images
Sample images showing assessments of the dermatologist (red), automated frameworks DBSCAN (blue) and FCM (green).
Kockara et al. BMC Bioinformatics 2010 11(Suppl 6):S26 doi:10.1186/1471-2105-11-S6-S26

28. Literature
• M. Ester, H.P. Kriegel, J. Sander, X. Xu
A density-based algorithm for discovering clusters in large spatial
databases with noise.
Proceedings of 2nd International Conference on Knowledge Discovery
and Data Mining (KDD96).
• A. Naprienko
Dichtebasierte Verfahren der Clusteranalyse raumbezogener Daten
am Beispiel von DBSCAN und Fuzzy-DBSCAN.
Universität der Bundeswehr München, student’s project, WT2011.
• J. Sander, M. Ester, H.P. Kriegel, X. Xu
Density-based clustering in spatial databases: the algorithm GDBSCAN
and its applications.
Data Mining and Knowledge Discovery, Springer, Berlin, 2 (2): 169–194.

29. Literature
• J.N Dharwa, A.R. Patel
A Data Mining with Hybrid Approach Based Transaction Risk Score
Generation Model (TRSGM) for Fraud Detection of Online Financial Transaction.
Proceedings of 2nd International Conference on Knowledge Discovery and
Data Mining (KDD96). International Journal of Computer Applications, Vol 16, No. 1, 2011.

30. Thank you very much!