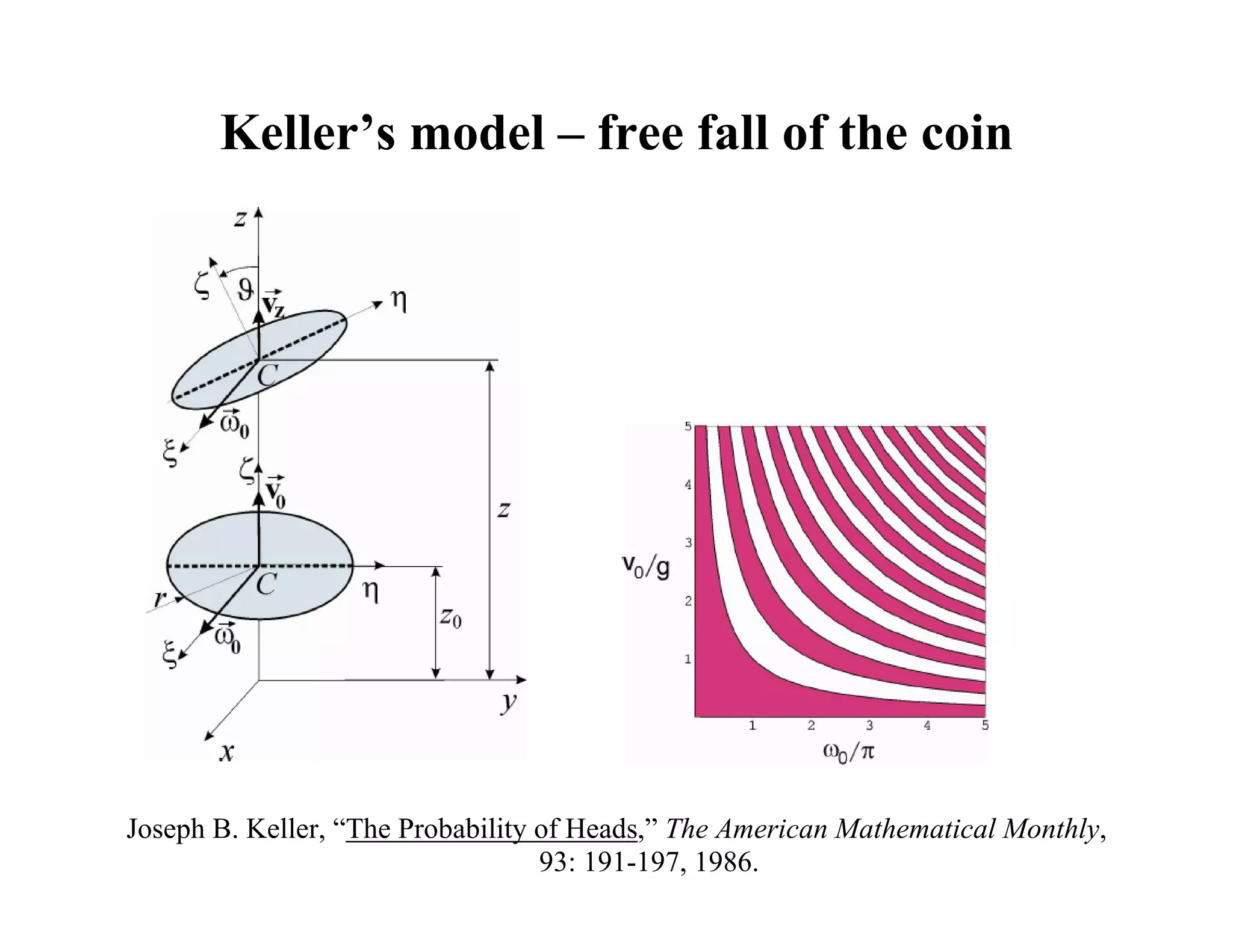
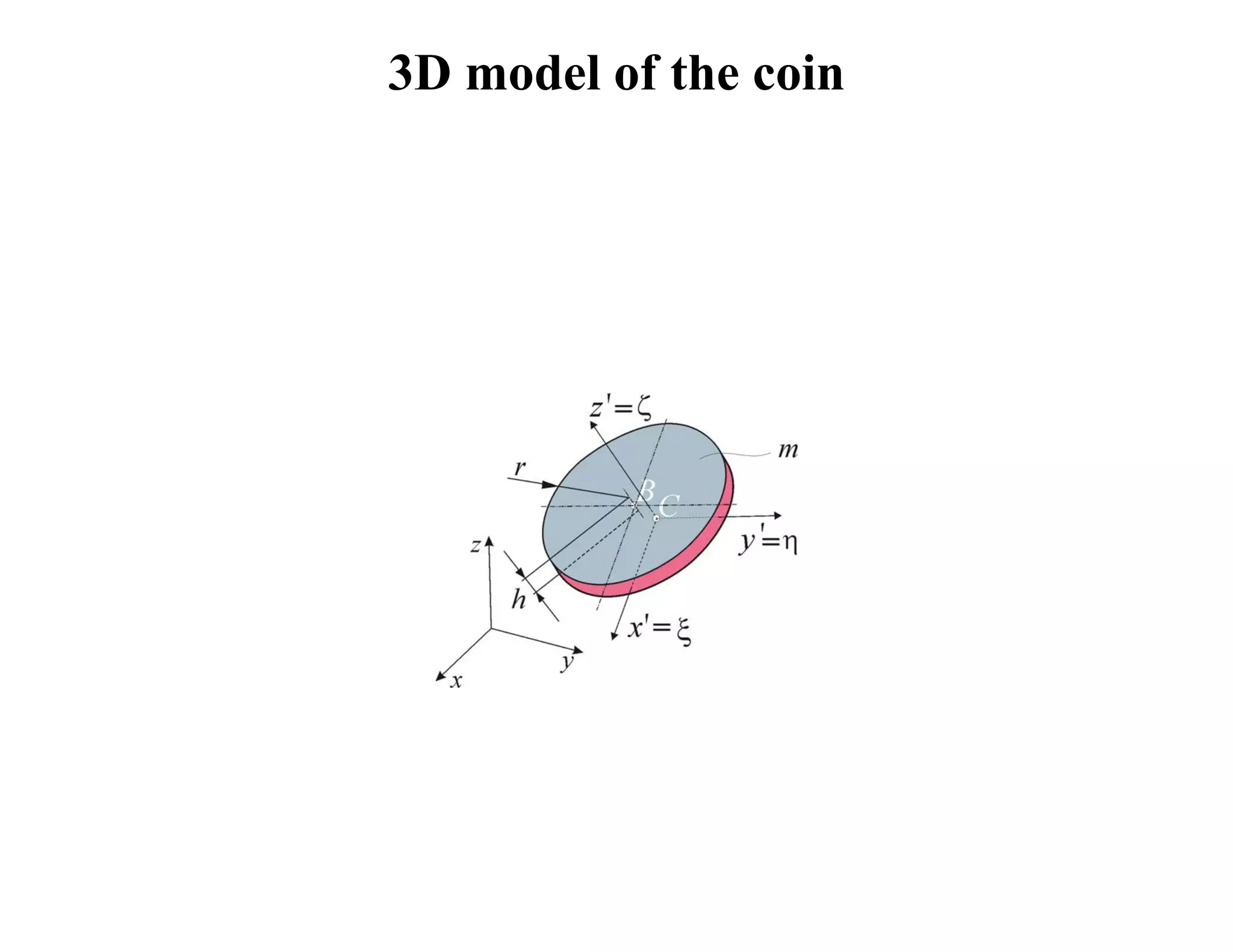
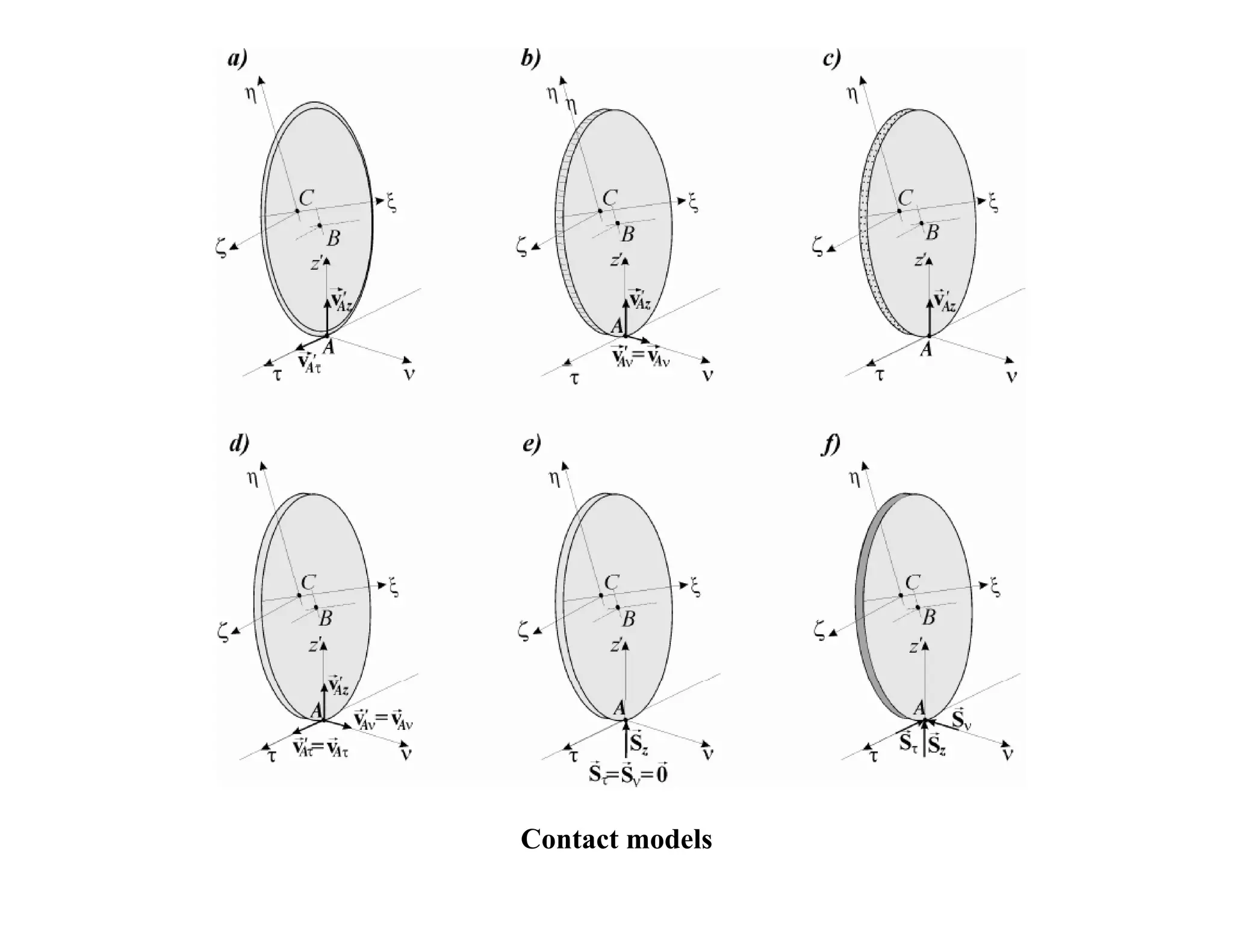
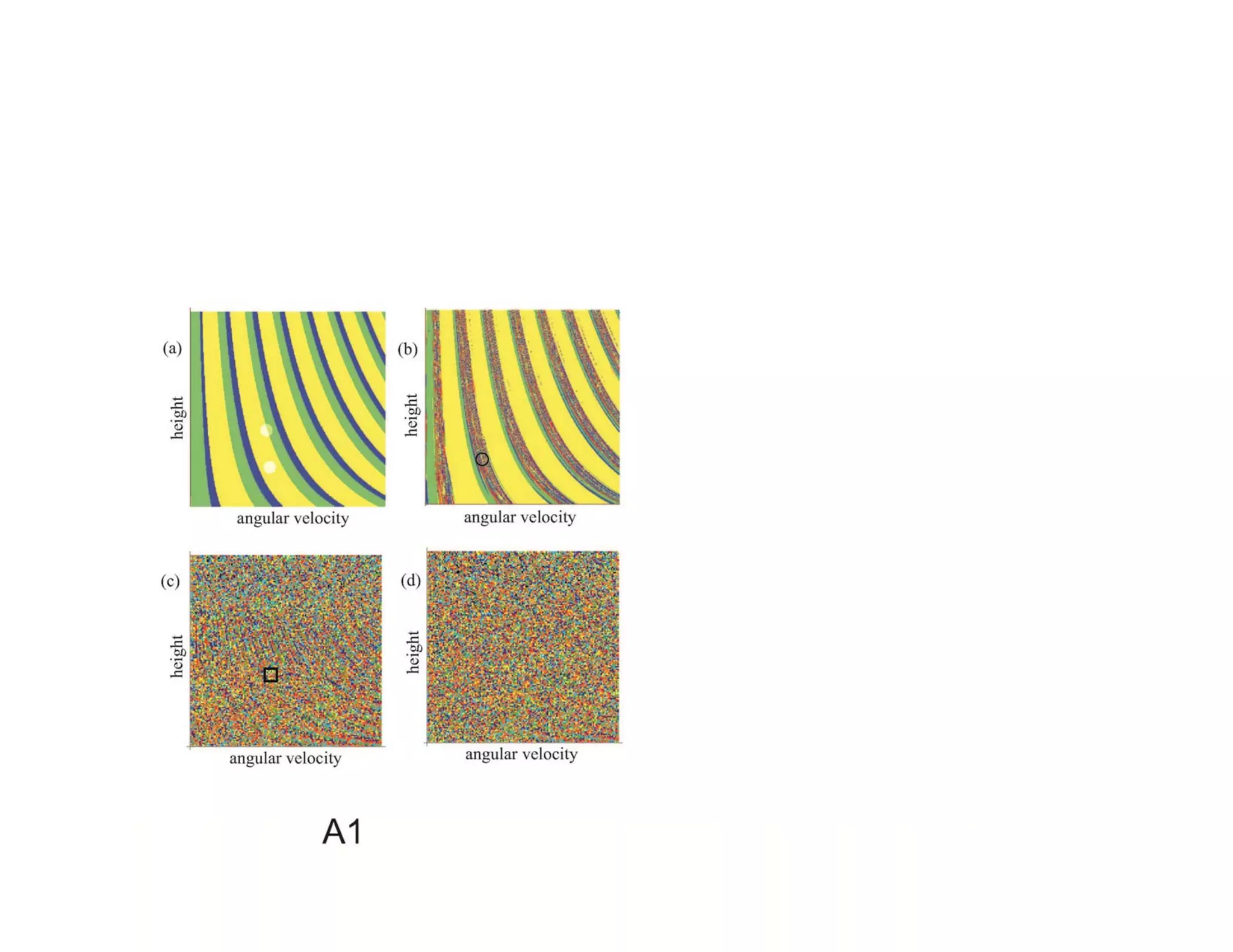
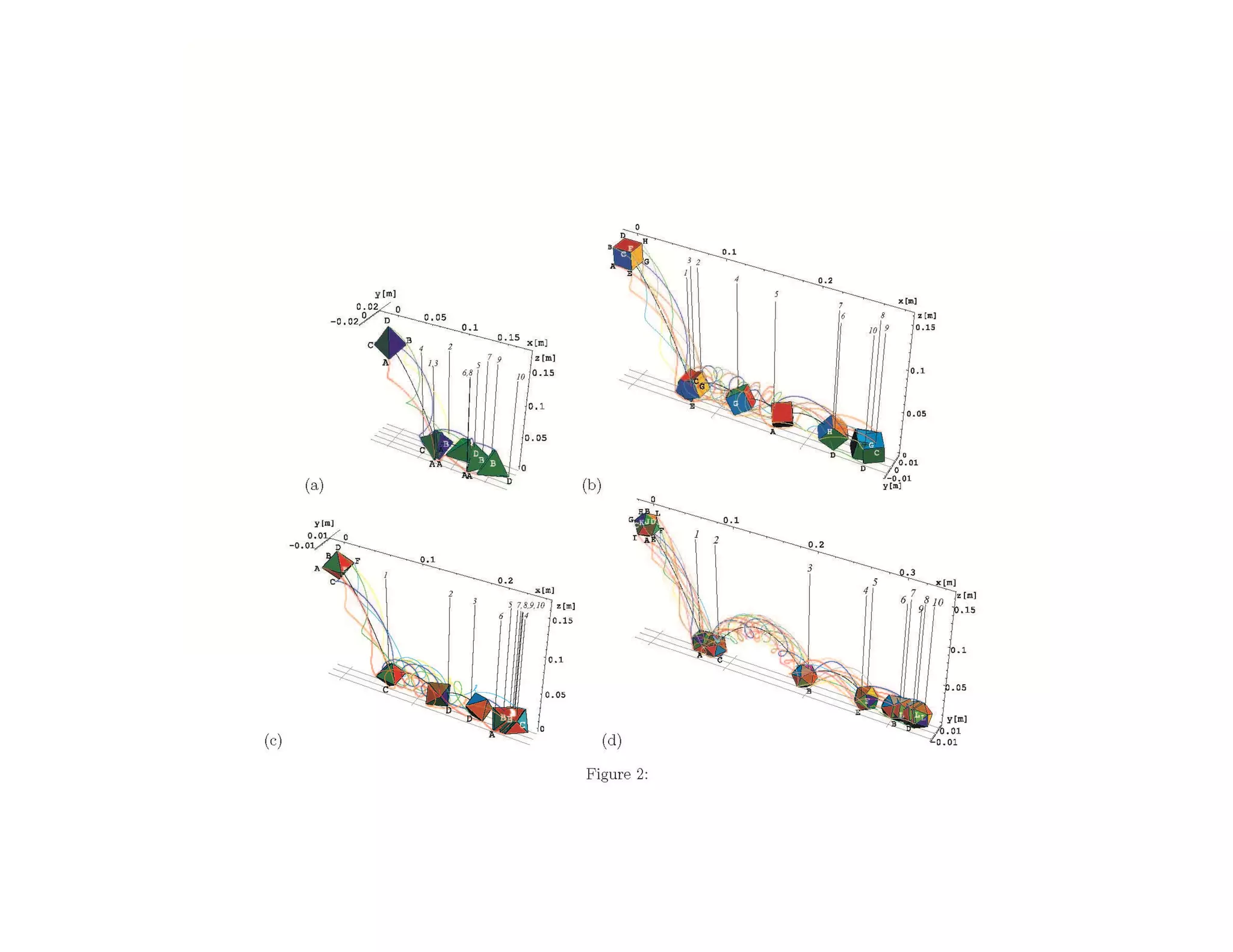
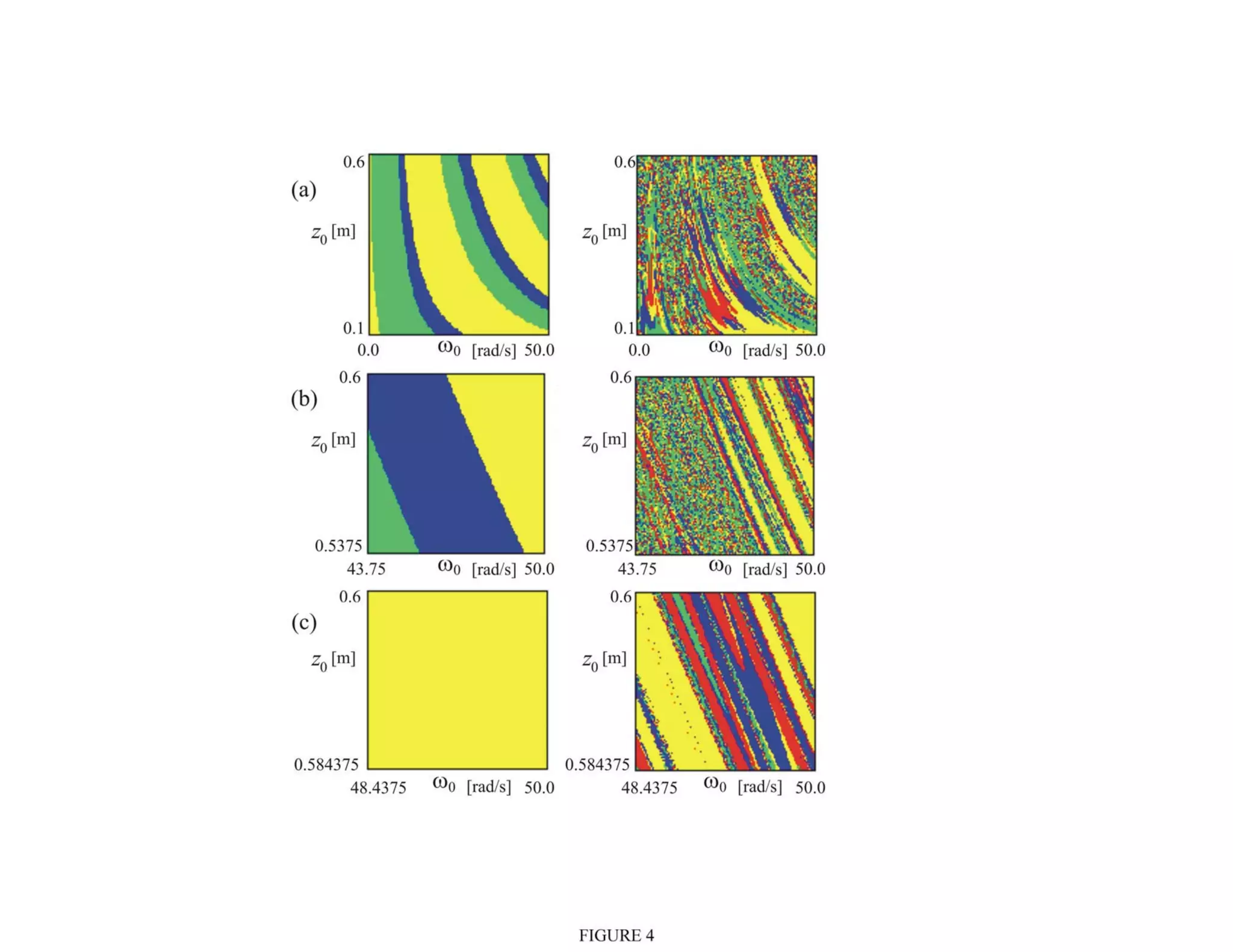
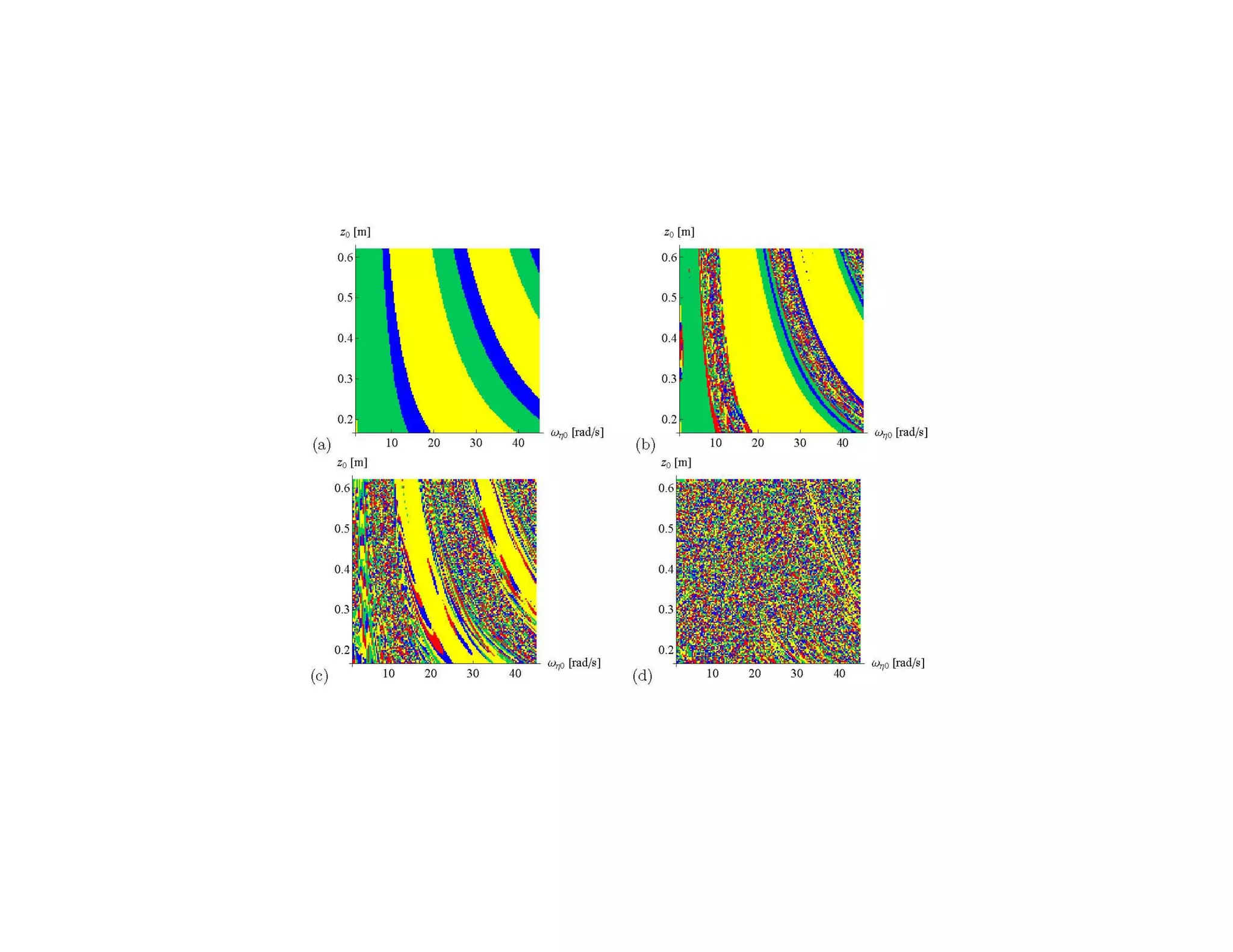
1) The document discusses whether dice rolls and other mechanical randomizers can truly produce random outcomes from a dynamics perspective. 2) It analyzes the equations of motion for different dice shapes and coin tossing, showing that outcomes are theoretically predictable if initial conditions can be reproduced precisely. 3) However, in reality small uncertainties in initial conditions mean mechanical randomizers can approximate random processes, even if they are deterministic based on their underlying dynamics.

1. Dynamics of dice gamess
Can the dice be fair by dynamics?
Tomasz Kapitaniak
Division of Dynamics,
Technical University of Lodz

3. Orzeł czy Reszka?
Tail or Head?
A Cara o Cruz?
Pile ou Face?
орeл или решкa?

4. Ἀριστοτέλης, Aristotélēs
Marble bust of Aristotle. Roman copy after a Greek bronze original by Lysippus c. 330 BC. The alabaster
mantle is modern

5. DICE

6. Generally, a die with a shape of convex polyhedron is fair by symmetry
if and only if it is symmetric with respect to all its faces. The polyhedra
with this property are called the isohedra.
Regular Tetrahedron Isosceles Tetrahedron Scalene Tetrahedron
Cube Octahedron Regular Dodecahedron
Octahedral Pentagonal Dodecahedron
Tetragonal Pentagonal Dodecahedron Rhombic Dodecahedron

7. Trapezoidal Dodecahedron Triakis Tetrahedron Regular Icosahedron
Hexakis Tetrahedron Tetrakis Hexahedron Triakis Octahedron
Trapezoidal Icositetrahedron Pentagonal Icositetrahedron Dyakis Dodecahedron
Rhombic Triacontahedron Hexakis Octahedron Triakis Icosahedron

8. Pentakis Dodecahedron Trapezoidal Hexecontahedron Pentagonal Hexecontahedron
Hexakis Icosahedron Triangular Dihedron Basic Triangular Dihedron
120 sides Move points up/down - 4N sides 2N sides
Basic Trigonal Trapezohedron
Sides have symmetry -- 2N Sides Triangular Dihedron
Trigonal Trapezohedron Move points in/out - 4N sides
Asymmetrical sides -- 2N Sides

10. GEROLAMO CARDANO (1501-1576)

11. Galileo Galilei (1564-1642)

12. Christian Huygens (1625-1695)

13. Joe Keller
Persi Diaconis

14. Keller’s model – free fall of the coin
Joseph B. Keller, “The Probability of Heads,” The American Mathematical Monthly,
93: 191-197, 1986.

15. 3D model of the coin

16. Contact models

17. Free fall of the coin: (a) ideal 3D, (b) imperfect 3D, (c) ideal 2D, (d) imperfect 2D.

18. Trajectories of the center of the mass of different coin models

19. Trajectories of the center of the mass for different initial conditions

21. Basins of attraction

23. Definition 1. The die throw is predictable if for almost all initial
conditions x0 there exists an open set U (x0 ϵ U) which is mapped
into the given final configuration.
Assume that the initial condition x0 is set with the inaccuracy є.
Consider a ball B centered at x0 with a radius є. Definition 1 implies
that if B ϲ U then randomizer is predictable.
Definition 2. The die throw is fair by dynamics if in the
neighborhood of any initial condition leading to one of the n final
configurations F1,...,Fi,...,Fn, where i=1,...,n, there are sets of points
β(F1),...,β(Fi),...,β(Fn), which lead to all other possible configurations
and a measures of sets β(Fi) are equal.
Definition 2 implies that for the infinitely small inaccuracy of the
initial conditions all final configurations are equally probable.

25. How chaotic is the coin toss ?
(a) (b)

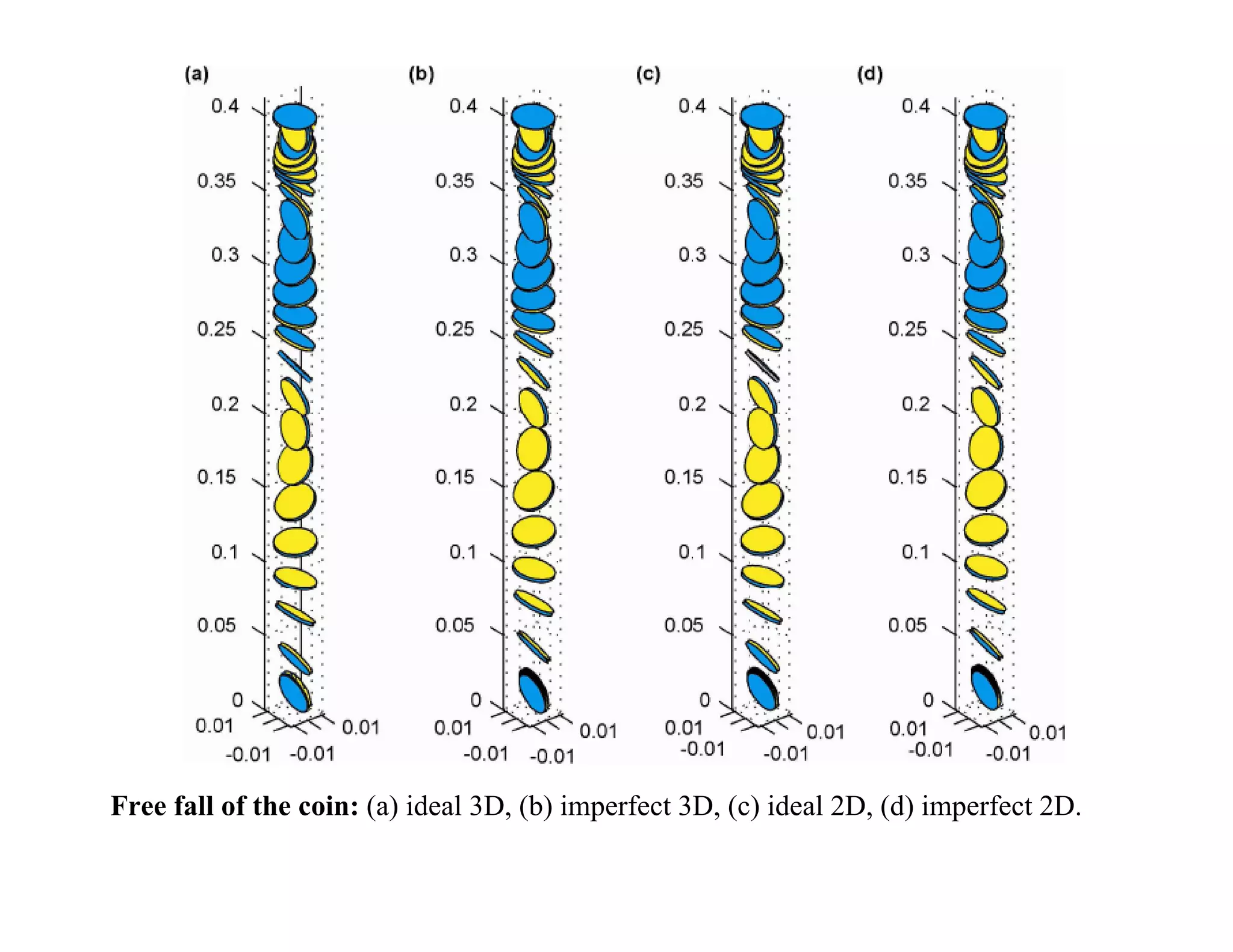
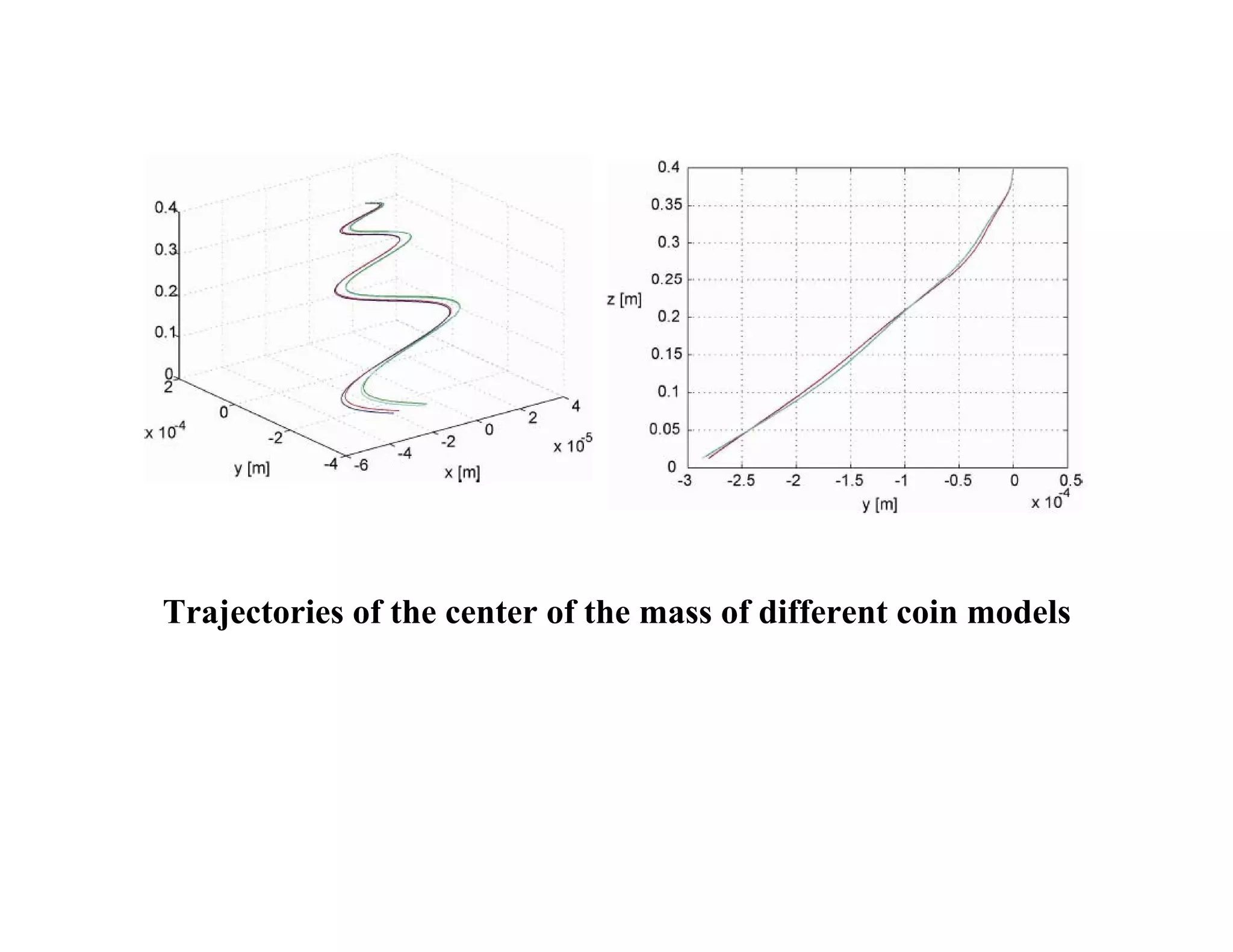
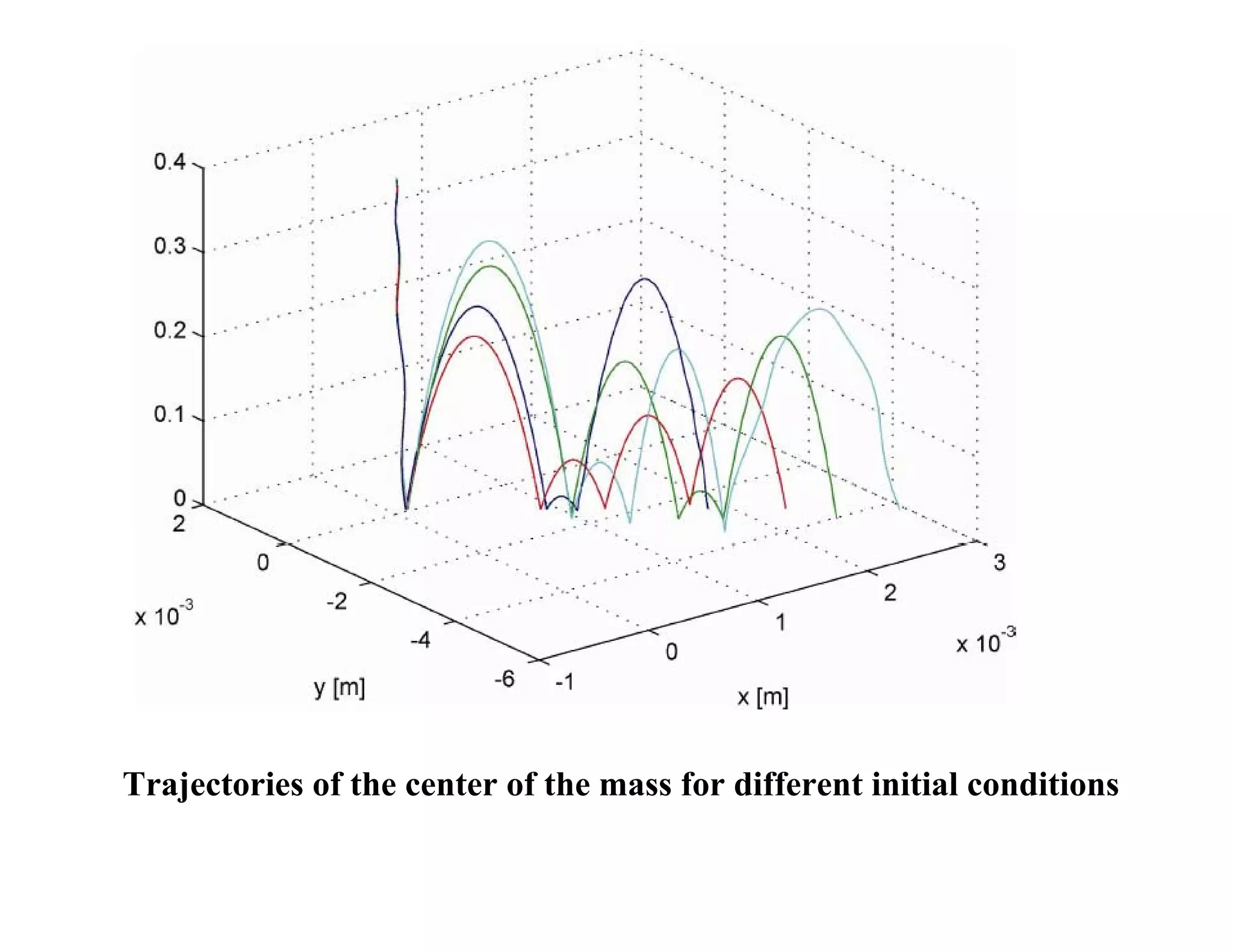
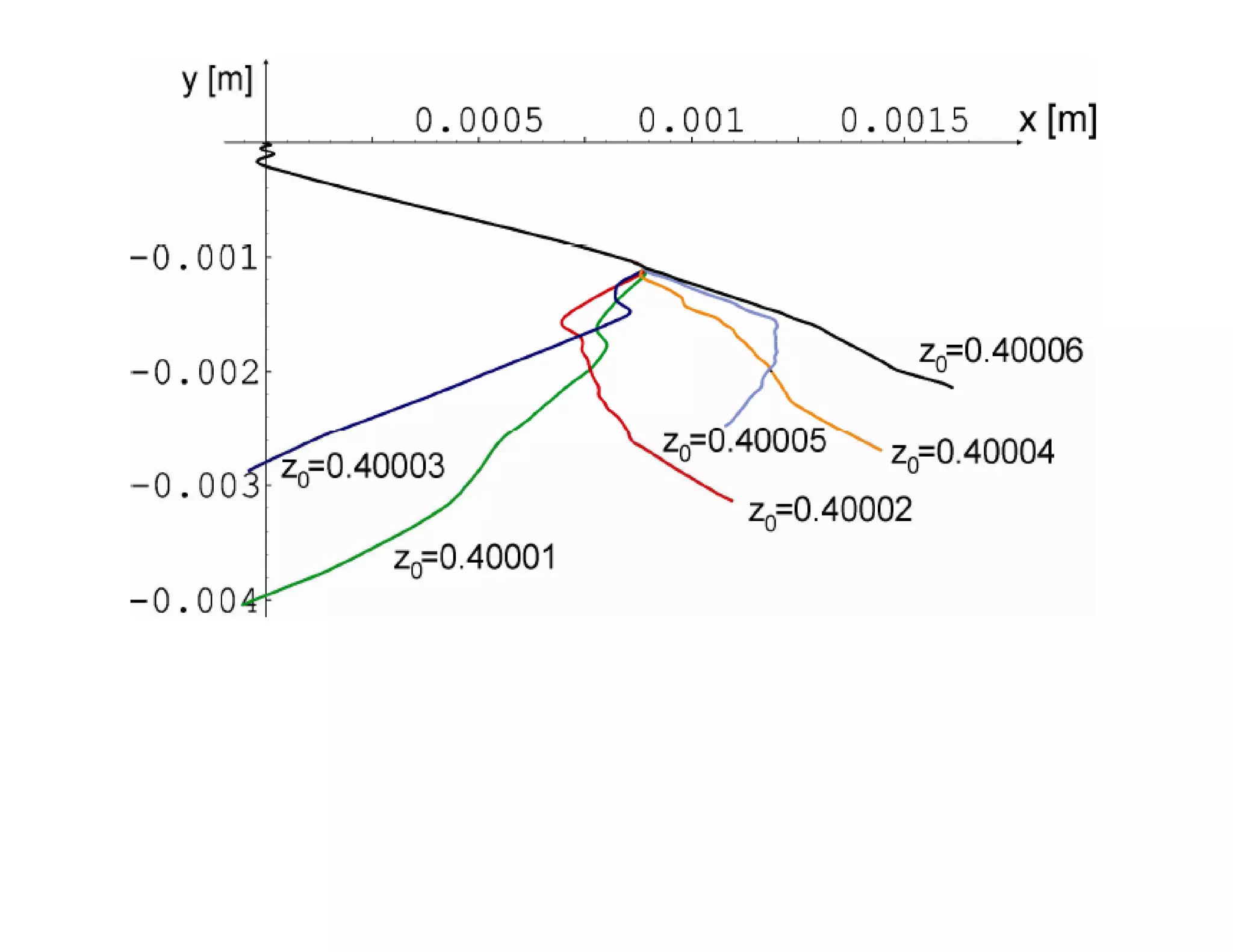
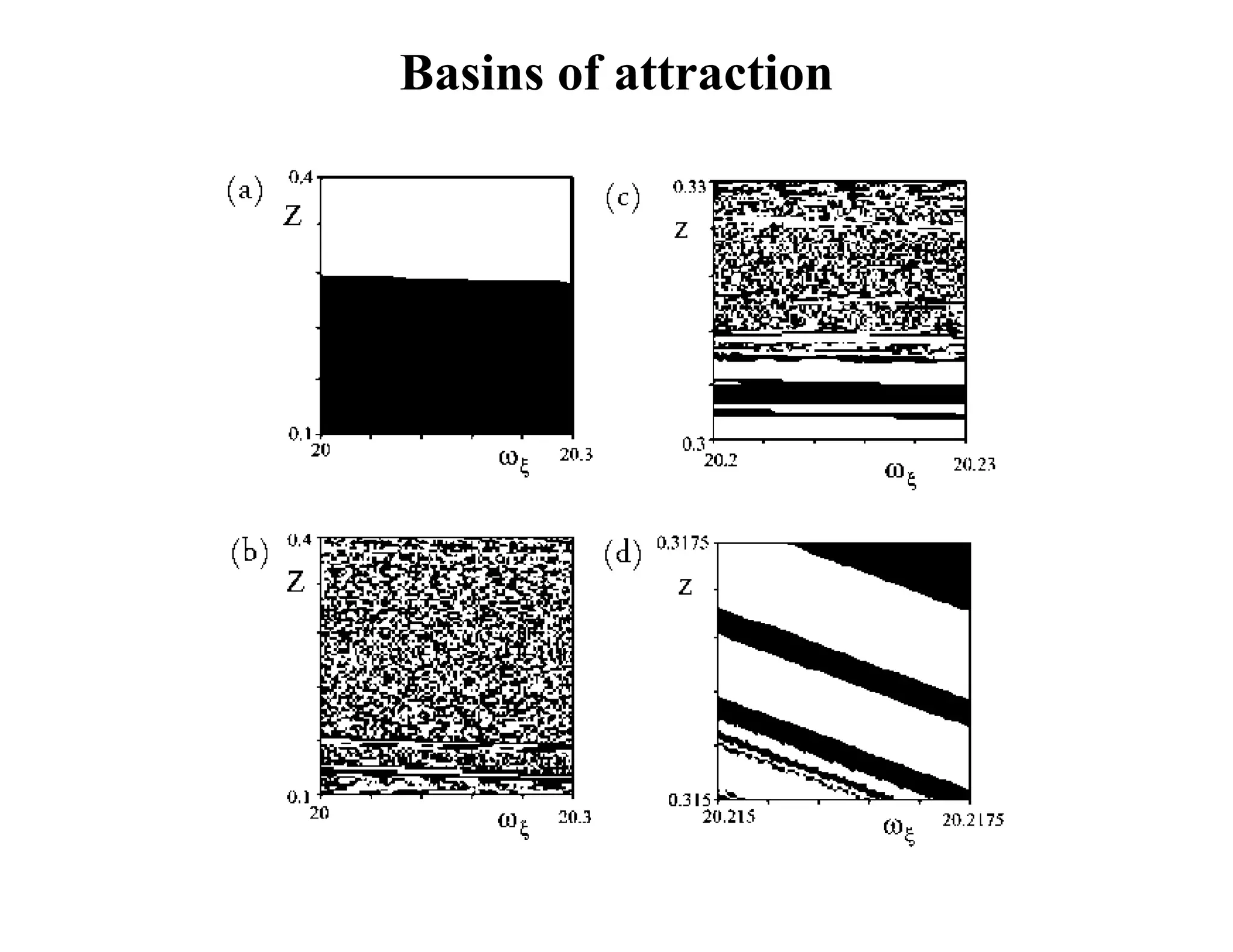
30. ωη 0 [rad/s] tetrahedron cube octahedron icosehedron
0 0.393 0.217 0.212 0.117
10 0.341 0.142 0.133 0.098
20 0.282 0.101 0.081 0.043
30 0.201 0.085 0.068 0.038
40 0.092 0.063 0.029 0.018
50 0.073 0.022 0.024 0.012
100 0.052 0.013 0.015 0.004
200 0.009 0.008 0.007 0.002
300 0.005 0.005 0.003 0.001
1000 0.003 0.002 0.001 0.000

31. In the early years of the previous century there was a general conviction
that the laws of the universe were completely deterministic. The
development of the quantum mechanics, originating with the work of
such physicists as Max Planck, Albert Einstein and Louis de Broglie
change the Laplacian conception of the laws of nature as for the
quantum phenomena the stochastic description is not just a handy trick,
but an absolute necessity imposed by their intrinsically random nature.
Currently the vast majority of the scientists supports the vision of a
universe where random events of objective nature exist. Contradicting
Albert Einstein's famous statement it seems that God Plays dice after all.
But going back to mechanical randonizers where quantum phenomena
have at most negligible effect we can say that:
God does not play dice in the casinos !

33. Главная / Новости науки
Выпадение орла или решки можно точно предсказать
Actualité : Pile ou face : pas tant de
hasard

35. Dynamics of Gambling: Origins of Randomness in Mechanical Systems;
Lecture Notes in Physics, Vol. 792, Springer 2010 – 48.00 Euro only !!
_________________
This monograph presents a concise discussion of the dynamics of
mechanical randomizers (coin tossing, die throw and roulette). The
authors derive the equations of motion, also describing collisions and
body contacts. It is shown and emphasized that, from the dynamical
point of view, outcomes are predictable, i.e. if an experienced player can
reproduce initial conditions with a small finite uncertainty, there is a
good chance that the desired final state will be obtained. Finally, readers
learn why mechanical randomizers can approximate random processes
and benefit from a discussion of the nature of randomness in mechanical
systems. In summary, the book not only provides a general analysis of
random effects in mechanical (engineering) systems, but addresses deep
questions concerning the nature of randomness, and gives potentially
useful tips for gamblers and the gaming industry.
_________________

37. Thank you
We are not responsible for what you lose in the casino!