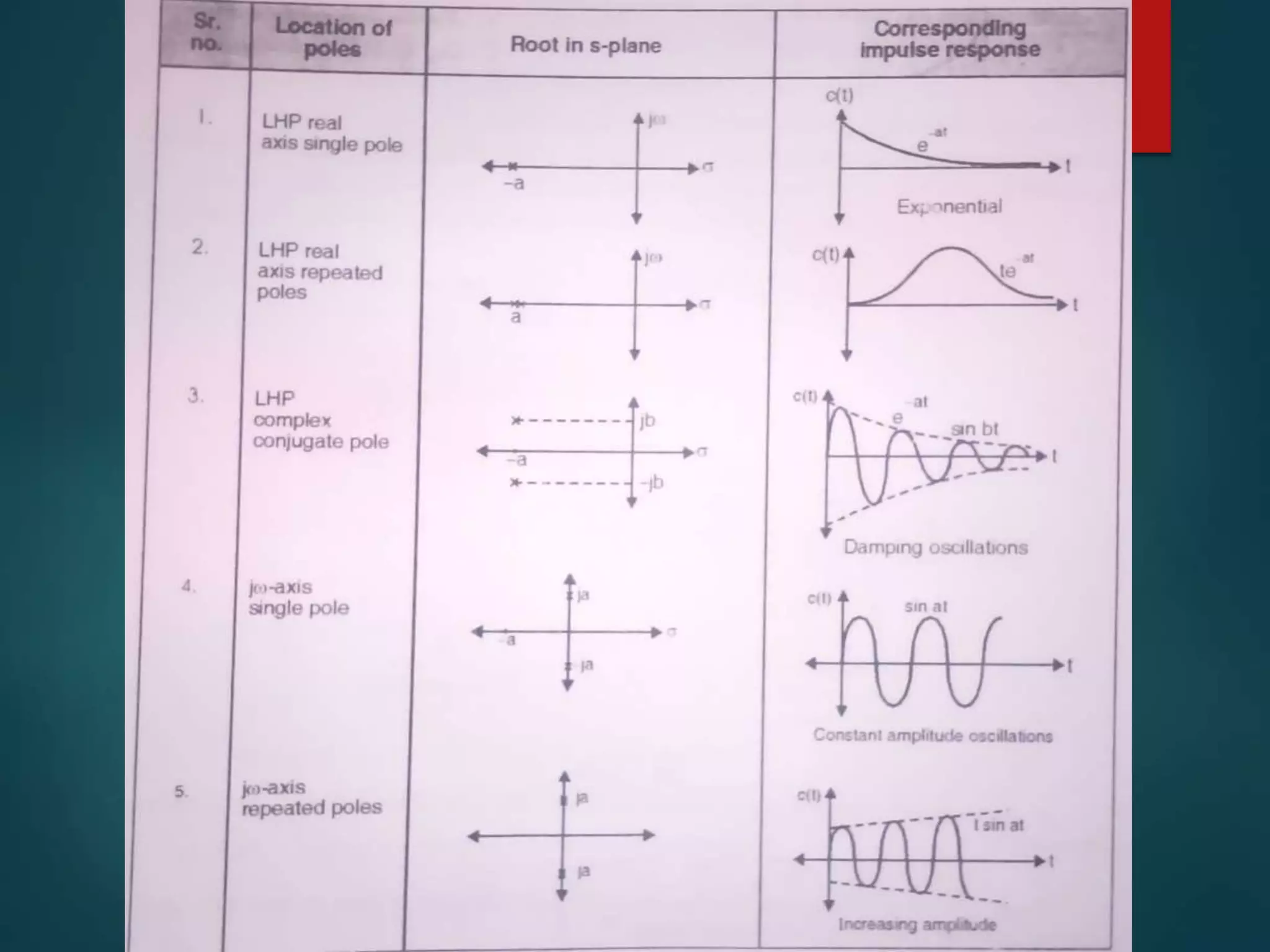
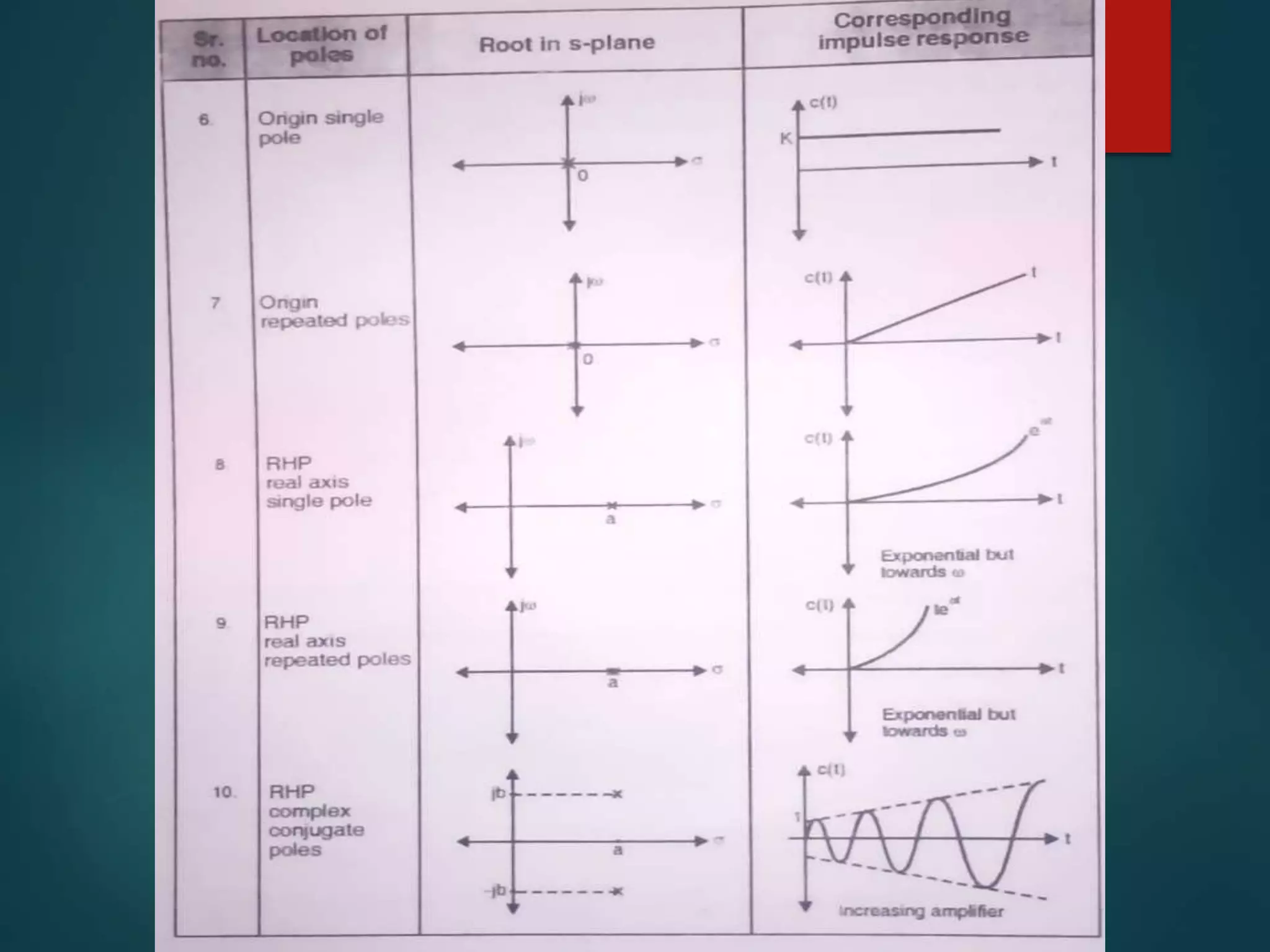
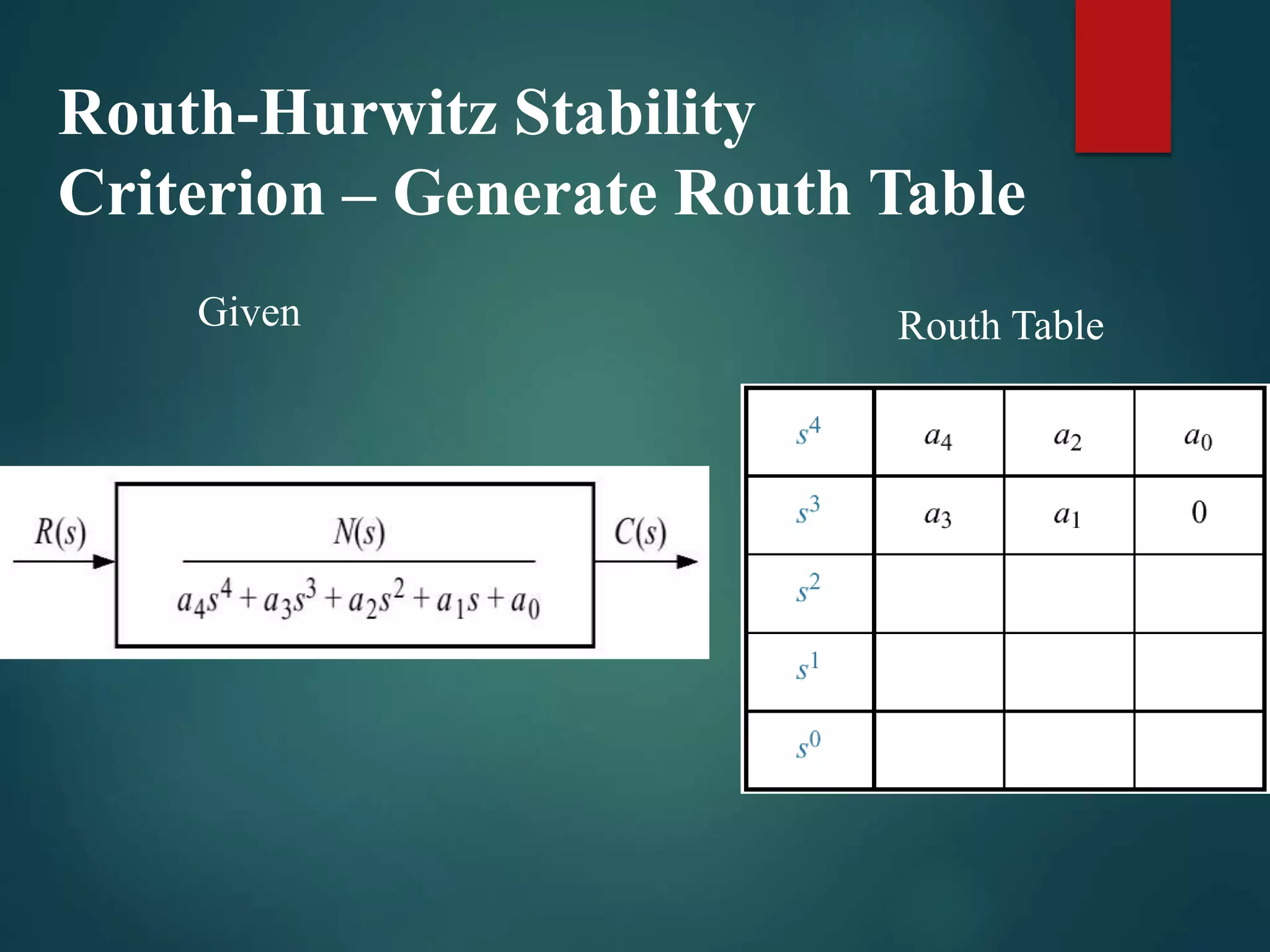
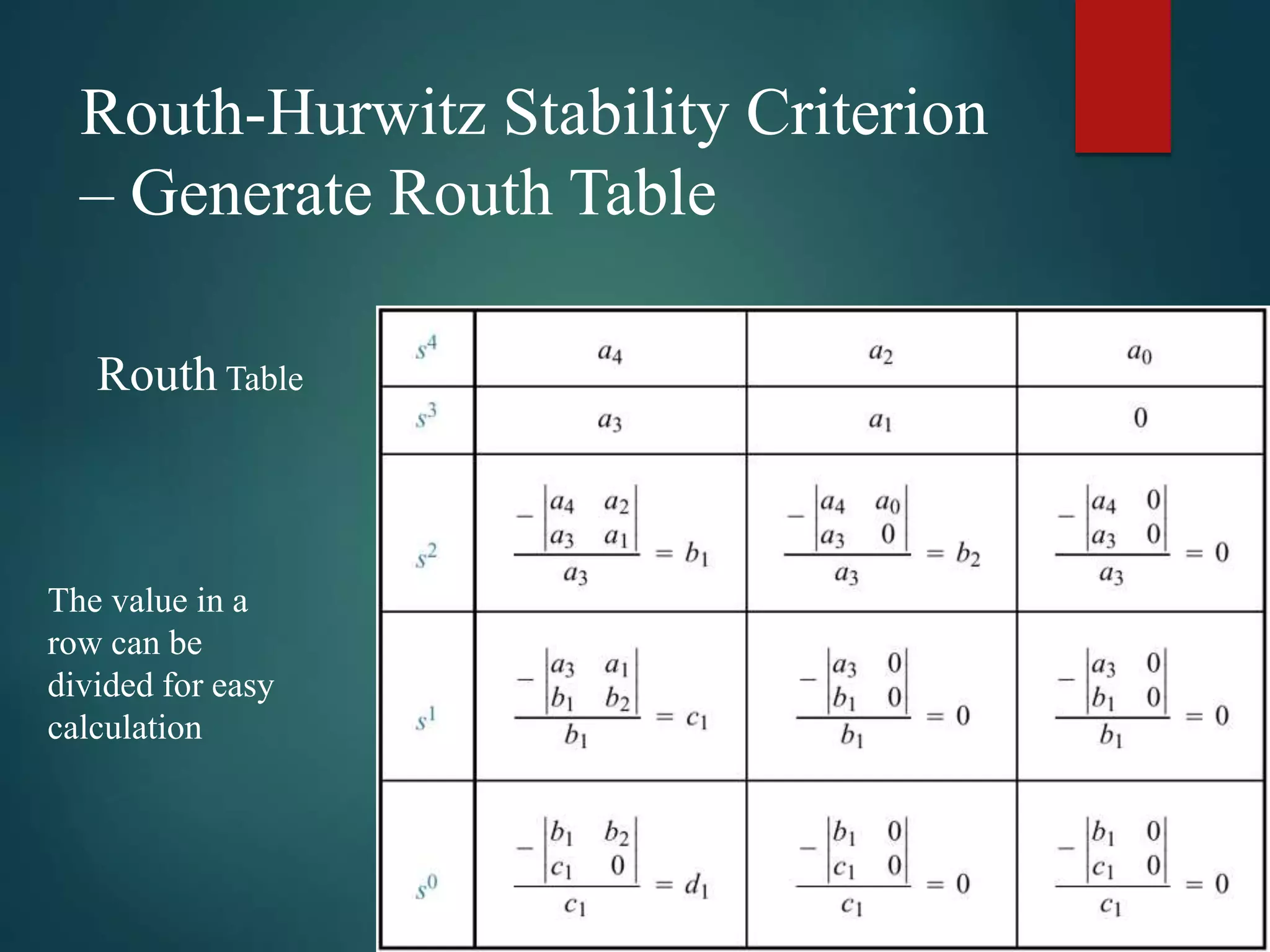
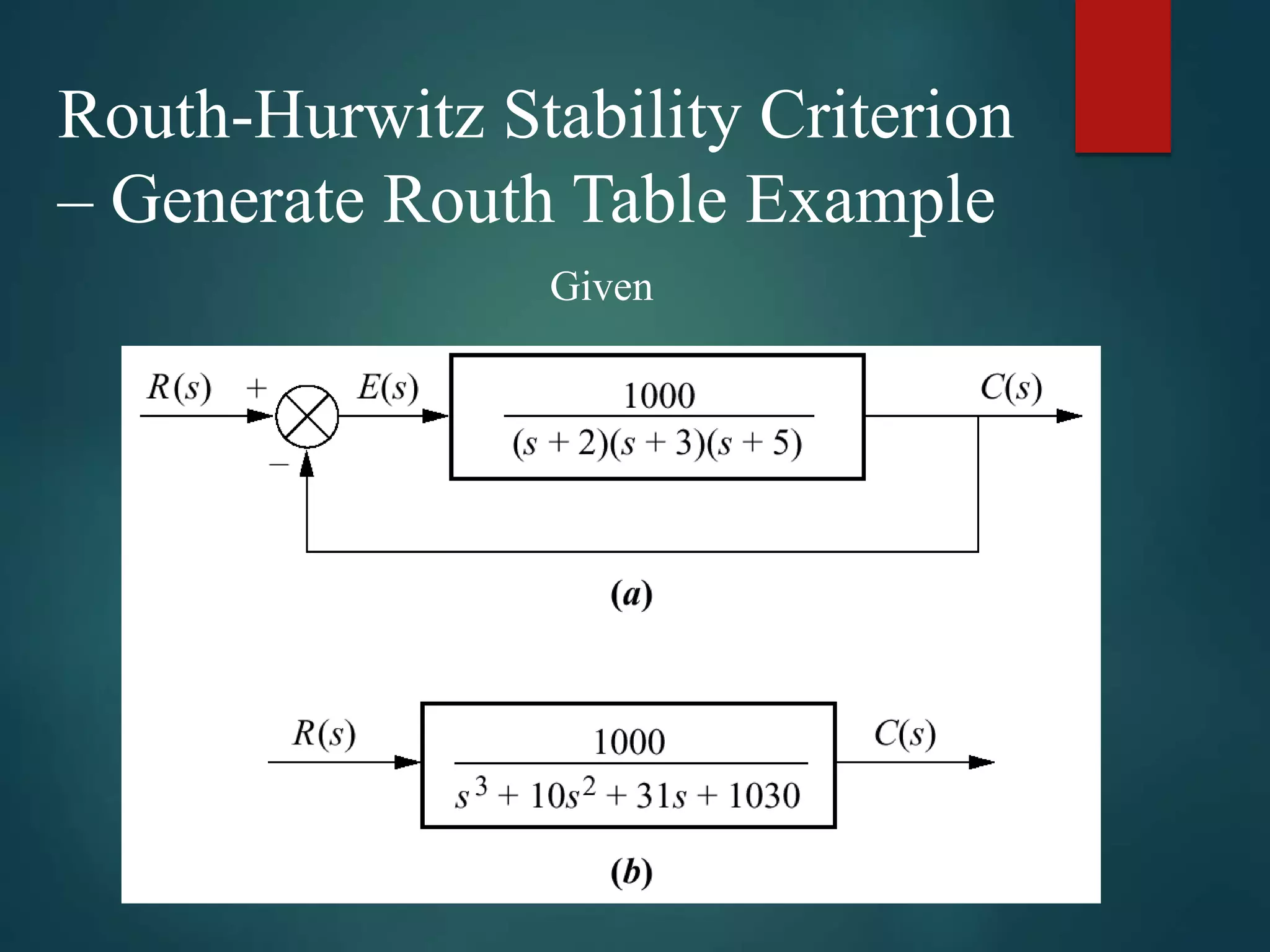
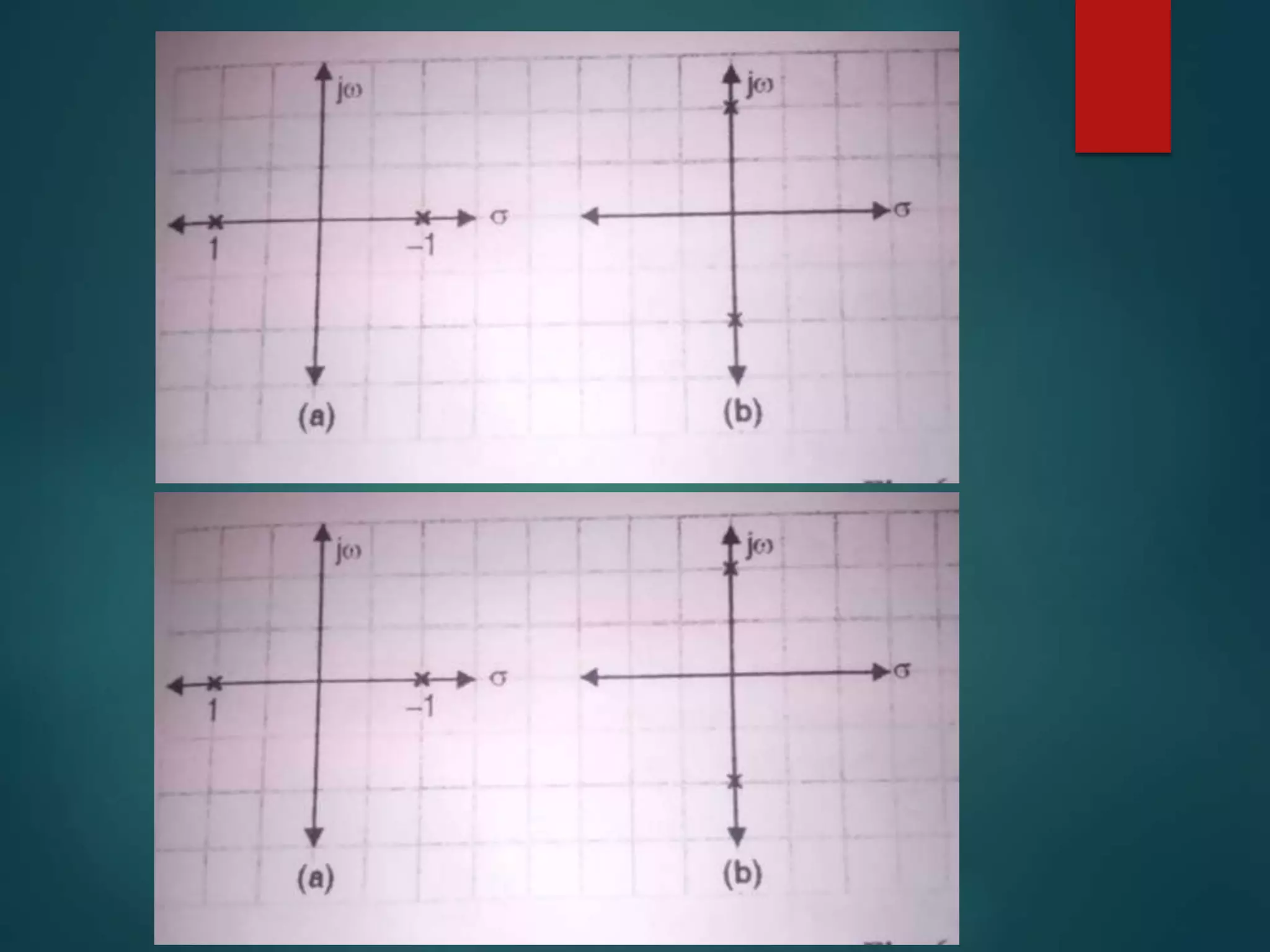
1. The document discusses the Routh-Hurwitz stability criterion, which is a test used to determine the stability of linear time-invariant systems by constructing a Routh array from the coefficients of the characteristic equation and analyzing it. 2. Special cases that can occur with the Routh array, such as a zero in the first column or an entire zero row, are explained along with their implications. 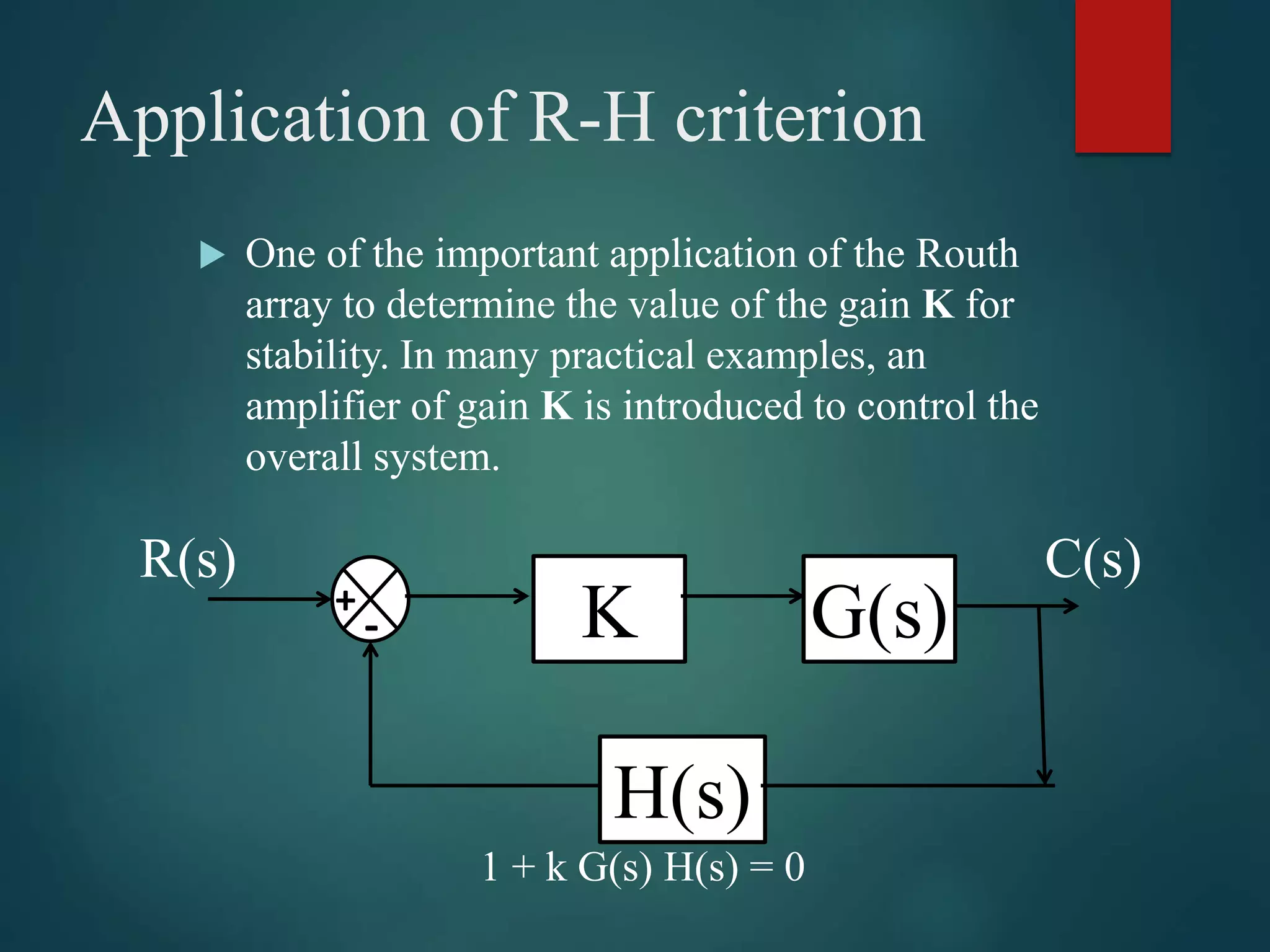3. An important application of the Routh-Hurwitz criterion is determining the range of values for a system gain K that ensures stability.

1. Gujarat Technical
University
BIRLA VISHWAKARMA
MAHAVIDYALAYA
ET Department
ROUTH-STABILITY CRITERSION
SUBMITED BY:-
APAR TRIVEDI :130080112057
VATSAL BODIWALA :140083111002
Under the Guidance :
Prof. Amit Chokasi
ET department, BVM

2. CONTENT
 The concept of stability
 The Routh-Hurwitz stability criterion
 The relative stability of feedback systems
 Design examples and MATLAB simulation
 Summary

3. The concept of stability
 A stable system is a dynamic system with a
bounded output to a bounded input (BIBO).
 absolute stability
 relative stability

4. Stability for LTI system
 A necessary and sufficient condition for a
feedback system to be stable is that all the poles of
the system transfer function have negative real
parts.
 Impulse response approach to zero when time lead
to infinite.

5. Routh-Hurwitz criterion
 Routh criterion:
This criterion states that the number
of roots of characteristic equation with positive
real parts is equal to the number of changes in
sign of the first column of the Routh array.

8. Routh-Hurwitz Stability
Criterion – Generate Routh Table
Given Routh Table

9. Routh-Hurwitz Stability Criterion
– Generate Routh Table
Routh Table
The value in a
row can be
divided for easy
calculation

10. Routh-Hurwitz Stability Criterion
– Generate Routh Table Example
Given

11. 𝑆3
+10𝑆2
+31S+1030

12. R-H Criterion – Special Cases
1. Zero in the first column
2. Zero in the entire row

13. Special Case 1:
 There are cases when the first element of the
Routh array is zero and the rest of the row is non-
zero. In such a case we cannot proceed to the next
stage without making some modifications.
 Example:
𝑆5
+𝑆4
+2𝑆3
+2𝑆2
+3S+5=0
2
3
4
5
S
S
S
S

0
1
1
2
2
2
 0
5
3

14. Special Case 2:
 There are cases when all the elements of a row in
the Routh array are zero. Obtaining a row of zeros
implies one of the four conditions.
i. Real roots but symmetrically located about the
j-axis.
ii. Conjugate roots on imaginary axis.
iii. Symmetrically located complex roots about the
j-axis.
iv. Repeated conjugate roots on the j-axis.

16. 𝑆6
+2𝑆5
+8𝑆4
+12𝑆3
+20𝑆2
+16𝑆+16=0
𝑎0=1, 𝑎1 = 2, 𝑎2=8, 𝑎3=12, 𝑎4=20, 𝑎5=16, 𝑎6=16
The Routh array is,
𝑆3
row is zero,
Take auxiliary equation using 𝑆4 row,
A(s)=2𝑆4+12𝑆2+16
𝑑𝐴(𝑠)
𝑑𝑠
=8𝑆3+24S
3
4
5
6
S
S
S
S
0
2
2
1
0
12
12
8
0
16
16
20
0
0
16

17. Application of R-H criterion
 One of the important application of the Routh
array to determine the value of the gain K for
stability. In many practical examples, an
amplifier of gain K is introduced to control the
overall system.
1 + k G(s) H(s) = 0
H(s)
G(s)+
- K
R(s) C(s)

18. ADVANTAGES
 Stability of the system can be determined without
actually solving the characteristic equation.
 No evaluation of determinants is required which
saves calculation time.
 It is not tedious or time consuming.
 It progresses systematically.
 For unstable system, it gives the number of roots
of characteristic equation having positive real
part.

19. ADVANTAGES
 Relative stability of the system can be ascertained.
 It helps in finding out the range of values of K for
system stability.
 It helps in finding out intersection point of root
locus with imaginary axis.
 By using this criterion, critical value of gain can
be determined and hence the frequency of
sustained oscillations.

20. DISADVANTAGES
 It is valid only for real coefficient of the
characteristic equation.
 It does not provide exact locations of the closed-
loop poles in left or right half of s-plane.
 It does not suggest methods of stabilizing an
unstable system.
 Applicable only to linear systems.