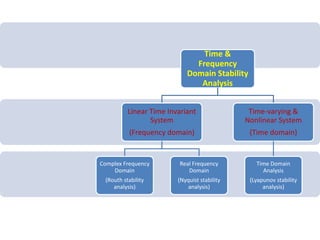
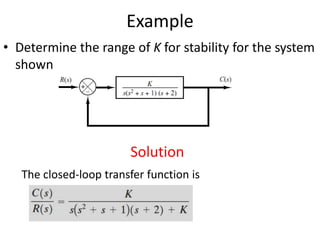
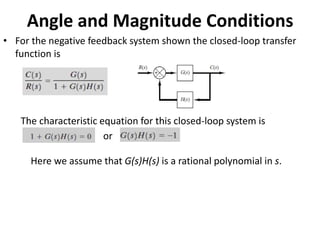
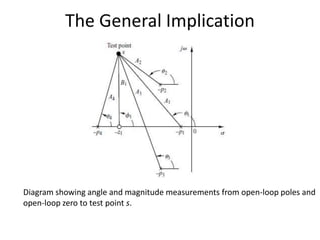
This document provides an overview of stability analysis in the frequency domain, including absolute stability, relative stability, Routh's stability criterion, and the root locus method. It defines absolute and relative stability and describes how Routh's stability criterion can be used to determine absolute stability by analyzing the signs of coefficients in the characteristic equation. The document also introduces the root locus method for analyzing how closed-loop poles move in the s-plane as the loop gain is varied.

1. Classical
Control
Third Year
Second Semester
Dr. Amr A. Sharawi
T.A. Amira Gaber
T.A. Asmaa Mohamed

2. STABILITY IN THE FREQUENCY
DOMAIN

3. Absolute Stability
• The most important characteristic of the dynamic
behavior of a control system is absolute stability.
• A control system is in equilibrium if, in the absence
of any disturbance or input, the output stays in the
same state.
• A linear time-invariant control system is stable if the
output eventually comes back to its equilibrium
state when the system is ONLY subjected to an
initial condition.

4. Absolute Stability
• A linear time-invariant (LTI) control system is
critically stable if oscillations of the output continue
forever.
• It is unstable if the output diverges without bound
from its equilibrium state when the system is
subjected to an initial condition.
• Thus, a LTI is stable, if it is a bounded-input-
bounded-output (BIBO) system.

5. Relative Stability
• An important system behavior (other than absolute
stability) to which we must give careful
consideration includes relative stability.
• Since a physical control system involves energy
storage, the output of the system, when subjected
to an input, cannot follow the input immediately
but exhibits a transient response before a steady
state can be reached.
• The duration of that transient response in the
practical sense is a measure of relative stability.

6. Time &
Frequency
Domain Stability
Analysis
Linear Time Invariant
System
(Frequency domain)
Complex Frequency
Domain
(Routh stability
analysis)
Real Frequency
Domain
(Nyquist stability
analysis)
Time-varying &
Nonlinear System
(Time domain)
Time Domain
Analysis
(Lyapunov stability
analysis)

7. Routh’s Stability Criterion
• The Routh’s stability criterion tells us whether or
not there are unstable roots in a polynomial
equation without actually solving for them.
• This stability criterion applies to polynomials with
only a finite number of terms.
• When the criterion is applied to a control system,
information about absolute stability can be
obtained directly from the coefficients of the
characteristic equation.

8. Routh’s Stability Analysis Procedure
• Write the polynomial in s in the following form:
where the coefficients are real quantities.
We assume that an an > 0; that is, any zero
root has been removed.
If any of the coefficients are zero or negative in the
presence of at least one positive coefficient,
a root or roots exist that are imaginary or that have
positive real parts.
Therefore, in such a case, the system is not stable.

9. Routh’s Stability Analysis Procedure
• If we are interested in only the absolute stability,
there is no need to follow the procedure further.
Note that all the coefficients must be positive.

10. Routh’s Stability Analysis Procedure
• If all coefficients are positive, arrange the coefficients of the
polynomial in rows and columns according to the following
pattern:

11. Routh’s Stability Analysis Procedure
• The process of forming rows continues until we run out of
elements. (The total number of rows is n+1). The
coefficients b1, b2, b3 , and so on, are evaluated as follows:

12. Routh’s Stability Analysis Procedure
• The evaluation of the b’s is continued until the remaining
ones are all zero.
• The same cross-multiplication pattern is followed in
evaluating the c’s, d’s, e’s, and so on. That is,

13. Routh’s Stability Analysis Procedure
This process is continued until the nth row has been
completed.
The complete array of coefficients is quasi-triangular.
In developing the array an entire row may be divided or
multiplied by a positive number in order to simplify the
subsequent numerical calculation without altering the
stability conclusion.

14. Implication of Routh’s Stability
Criterion
• Routh’s stability criterion states that the number of
roots of the characteristic equation with positive
real parts is equal to the number of changes in sign
of the coefficients of the first column of the array.
• The necessary and sufficient condition that all roots
of the characteristic equation lie in the left-half s-
plane is that all the coefficients of the characteristic
equation be positive and all terms in the first
column of the array have positive signs.

15. Example 5–11 – p. 214 – Ogata V
• Apply Routh’s stability criterion to the following
third-order polynomial:
• where all the coefficients are positive numbers.

16. Solution
• Routh’s array:
The condition that all roots have negative real parts is
given by

17. Example 5–12 – p. 214 – Ogata V
• Consider the following polynomial:
Solution
The first two rows can be obtained directly from the
given polynomial.
The second row can be divided by 2

18. Solution
• Having done so we get
𝑠3
1 2 0
We proceed with the remainder of the array as follows
The number of changes in sign of the coefficients in the
first column is 2.
This means that there are two roots with positive real
parts.

19. Special Cases
• If a first-column term in any row is zero, but the
remaining terms are not zero or there is no
remaining term, then the zero term is replaced by a
very small positive number ε and the rest of the
array is evaluated.

20. Example
• Consider the following equation:
The array of coefficients is
Now that the sign of the coefficient above the zero (ε) is
the same as that below it, it indicates that there are a pair
of imaginary roots (in that case at s = ±j).

21. Special Cases (Contd.)
• If, however, the sign of the coefficient above the
zero (ε) is opposite that below it, it indicates that
there are two sign changes of the coefficients in the
first column.
• In that case there are two coincident roots in the
right-half s-plane.

22. Relative Stability Analysis
• Routh’s stability criterion provides the answer to
• the question of absolute stability.
• This, in many practical cases, is not sufficient.
• We usually require information about the relative
stability of the system.
• A useful approach for examining relative stability is to
shift the s-plane axis and apply Routh’s stability
criterion.
• That is, we substitute
𝑠 = 𝑠−σ

23. Relative Stability Analysis
• into the characteristic equation of the system, write
the polynomial in terms of 𝑠 andapply Routh’s
stability criterion to the new polynomial in 𝑠
• The number of changes of sign in the first column of
the array developed for the polynomial in 𝑠 is equal
to the number of roots that are located to the right
of the vertical line s = –σ.
• Thus, this test reveals the number of roots that lie
to the right of the vertical line s = –σ.

24. Application of Routh’s Stability Criterion
to Control-System Analysis
• It is possible to determine the effects of changing
one or two parameters of a system by examining
the values that cause instability, particularly by
determining the stability range of one (or more)
parameter value.

25. Example
• Determine the range of K for stability for the system
shown.
Solution
The closed-loop transfer function is

26. Example (Contd.)
• The characteristic equation is
Routh’s array becomes
For stability, K must be positive, and all coefficients in
the first column must be positive. Therefore,

27. THE ROOT LOCUS METHOD

28. Introduction
• The basic characteristic of the transient response of a closed-loop
system is closely related to the location of the closed-loop poles.
• If the system has a variable loop gain, then the location of the
closed-loop poles depends on the value of the loop gain chosen.
• It is important, therefore, that the designer know how the closed-
loop poles move in the s plane as the loop gain is varied.
• From the design viewpoint, in some systems simple gain
adjustment may move the closed-loop poles to desired locations.
• If the gain adjustment alone does not yield a desired result,
addition of a compensator to the system will become necessary.
• The closed-loop poles are the roots of the characteristic equation.

29. The Concept
• The root-locus method is one in which the roots of the
characteristic equation are plotted for all values of a
system parameter, which will be assumed to be the
gain of the open-loop transfer function, unless
otherwise stated.
• The roots corresponding to a particular value of this
parameter can then be located on the resulting graph.
• It is desired that the designer have a good
understanding of the method for generating the root
loci of the closed-loop system, both by hand and by use
of a computer software program like MATLAB.

30. Angle and Magnitude Conditions
• For the negative feedback system shown the closed-loop transfer
function is
The characteristic equation for this closed-loop system is
or
Here we assume that G(s)H(s) is a rational polynomial in s.

31. Angle and Magnitude Conditions
• Since G(s)H(s) is a complex quantity, the characteristic can be split
into two equations by equating the angles and magnitudes of both
sides, respectively, to obtain

32. Angle and Magnitude Conditions
• The values of s that fulfill both the angle and
magnitude conditions are the roots of the
characteristic equation, or the closed-loop poles.
• A locus of the points in the complex plane satisfying
the angle condition alone is the root locus.
• The roots of the characteristic equation (the closed-
loop poles) corresponding to a given value of the
gain can be determined from the magnitude
condition.

33. The General Implication
• Generally, G(s)H(s) involves a gain parameter K, and the characteristic
equation may be written as
Then the root loci for the system are the loci of the closed-loop poles
as the gain K is varied from 0 to ∞.
The angles of the complex quantities originating from the open-loop
poles and open-loop zeros to a test point s are measured in the
counterclockwise direction.
In order that a test point lie on (i.e., be part of) the root locus, it
must satisfy the angle and magnitude conditions.

34. The General Implication
• For example, if G(s)H(s) is given by
where –p2 and –p3 are complex-conjugate poles, then the angle
of G(s)H(s) is
where 𝜙1 , θ1 , θ2 , θ3 , and θ4 are measured counterclockwise.
The magnitude of G(s)H(s) for this system is
where A1, A2, A3, A4, and B1 are the magnitudes of the complex
quantities s+p1, s+p2, s+p3, s+p4, and s+z1, respectively.

35. The General Implication
Diagram showing angle and magnitude measurements from open-loop poles and
open-loop zero to test point s.

36. Very Important
• Because the open-loop complex-conjugate poles and complex-
conjugate zeros, if any, are always located symmetrically about the
real axis, the root loci are always symmetrical w.r.t. this axis.
• Therefore, we only need to construct the upper half of the root loci
and draw the mirror image of the upper half in the lower-half s plane.
• Because graphical measurements of angles and magnitudes are
involved in the analysis, we find it necessary to use the same
divisions on the abscissa as on the ordinate axis when sketching the
root locus on graph paper.
• The number of individual root loci for a system is the same as the
number of open-loop poles.
• The starting points of the root loci (the points corresponding to K = 0)
are open-loop poles.

37. Example 6–1 – p. 273 – Ogata V
• Consider the negative feedback system given by:
1. Sketch the root-locus plot
2. Determine the value of K such that the damping ratio of the pair
of dominant complex-conjugate closed-loop poles is 0.5.
Solution
For the given system, the angle condition becomes

38. Example 6–1 – p. 273 – Ogata V
• The magnitude condition is
Computational Steps
1. Determine the root loci on the real axis.
To determine the root loci on the real axis, we select a test point, s.
a) If s > 0, then:
(angle condition not satisfied)
b) If 0 > s > -1, then:
Thus
(angle condition satisfied)

39. Example 6–1 – p. 273 – Ogata V
c) If -1 > s > -2, then:
Thus
(angle condition not satisfied)
d) If -2 > s > -∞, then:
= 180°
Thus
-540° (angle condition satisfied)
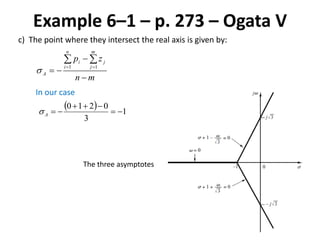
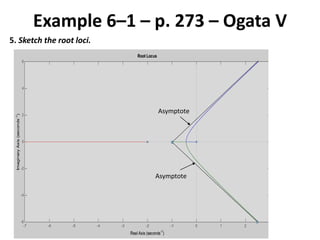
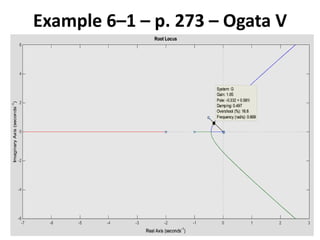
Thus, the portion of the real axis that lies on the root locus is given by:
 ]0,1[]2,[ S

40. Example 6–1 – p. 273 – Ogata V
2. Determine the asymptotes of the root loci.
The asymptotes of the root loci as s approaches infinity must lie on the real axis.
This is because the root loci are symmetrical about the real axis.
They can be determined as follows:
a) Number of asymptotes = n – m,
where n = number of poles & m = number of zeros.
In our case n = 3 & m = 0, so there are three asymptotes.
b) The angles of the asymptotes are given by:
 ,
12180
mn
k
k


 k = 0, 1, 2, . . ., n - m
In our case the angles are given by θo = 60°, θ1 = 180°, θ2 = 300°,
And the asymptotes with the three negative angles coincide with the other
three.

41. Example 6–1 – p. 273 – Ogata V
c) The point where they intersect the real axis is given by:
mn
zp
n
i
m
j
ji
A



 
 1 1

In our case
  1
3
0210


A
The three asymptotes

42. Example 6–1 – p. 273 – Ogata V
3. Determine the breakaway point.
To plot root loci accurately, we must find the breakaway point, where the root-locus
branches originating from the poles break away from the real axis and move into the
complex plane, as K is increased.
The breakaway point corresponds to a point in the s plane where multiple roots of
the characteristic equation occur.
To find the breakaway point let us write the characteristic equation as
where A(s) and B(s) do not contain K.
f(s) = 0 has multiple roots at points where
Proof
Suppose that f(s) has multiple roots of order r, where r ≥ 2.
Then f(s) may be written as

43. Example 6–1 – p. 273 – Ogata V
     
     
     121
31
2
1
1
...
......
...
)(





n
r
n
r
n
r
ssssss
ssssss
ssssssr
ds
sdf
0
)(
1

ssds
sdf
Now
where

44. Example 6–1 – p. 273 – Ogata V
The particular value of K that will yield multiple roots of the characteristic equation
is obtained from
Thus
or
0)(')()(')()(')()(')(  sKAsAsAsBsBsAsAsB
0)()(  sKAsB
Thus

45. Example 6–1 – p. 273 – Ogata V
Next we have
= 0
This confirms that the breakaway points can be simply determined from the roots of
If a point at which dK/ds = 0 is on a root locus, it is an actual breakaway or break-
in point. Otherwise, it is not.
In our case the characteristic equation G(s) + 1 = 0 is given by
or
so

46. Example 6–1 – p. 273 – Ogata V
The two roots are given by
Since the breakaway point must lie on a root locus between 0 and –1, it is clear
that s = –0.4226 corresponds to the actual breakaway point. Point s = –1.5774 is not
on the root locus. Hence, this point is not an actual breakaway or break-in point.
In fact
4. Determine the points where the root loci cross the imaginary axis.
let s = jω in the characteristic equation, equate both the real part and the imaginary
part to zero, and then solve for ω and K. For the present system, the characteristic
equation, with s = jω, is
or

47. Example 6–1 – p. 273 – Ogata V
Equating both the real and imaginary parts of this last equation to zero, respectively,
we obtain
from which
Thus, root loci cross the imaginary axis at 𝜔 = ± 2 and the value of K at the
crossing points is 6.
Also, a root-locus branch on the real axis touches the imaginary axis at ω = 0.
The value of K is zero at this point.

48. Example 6–1 – p. 273 – Ogata V
5. Sketch the root loci.
Asymptote
Asymptote

49. Example 6–1 – p. 273 – Ogata V
6. Determine the point on the root locus where the damping ration of the
dominant poles is 0.5.
Closed-loop poles with ζ = 0.5 lie on lines passing through the origin and making
angles with the negative real axis given by ±cos-1 ζ = ±cos-1 0.5 = ±60° with the
negative real axis.
From the previous slide such closed loop poles are approximately given by
s = -0.33 ± j 0.58 complex rad/s
The value of K that yields such poles is found from the magnitude condition as
follows:
𝐾 = 𝑠 𝑠 + 1 𝑠 + 2 𝑠=−0.33+𝑗0.58 ≈ 1.05
The basic construction can be found on the next slide.

50. Example 6–1 – p. 273 – Ogata V