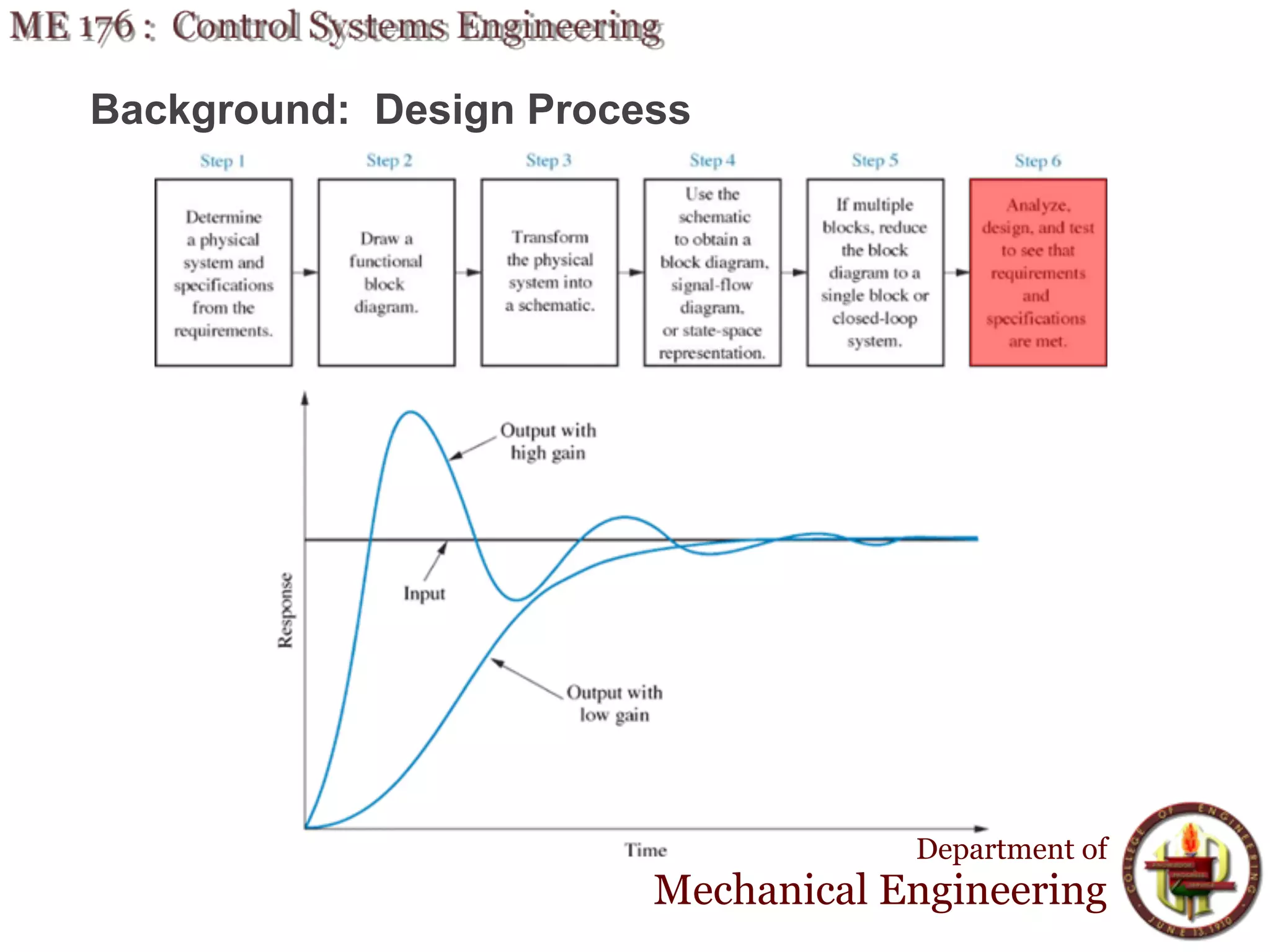
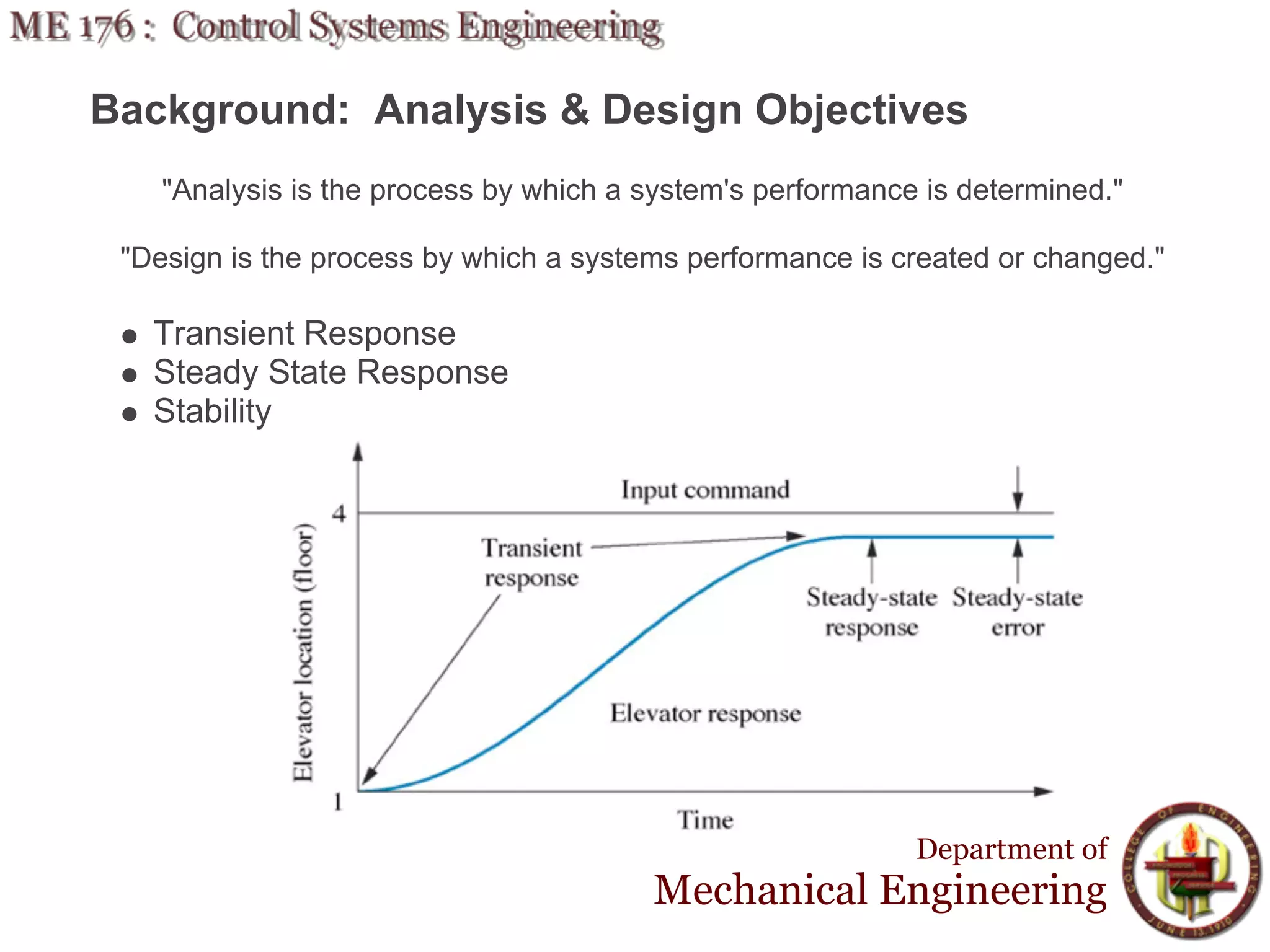
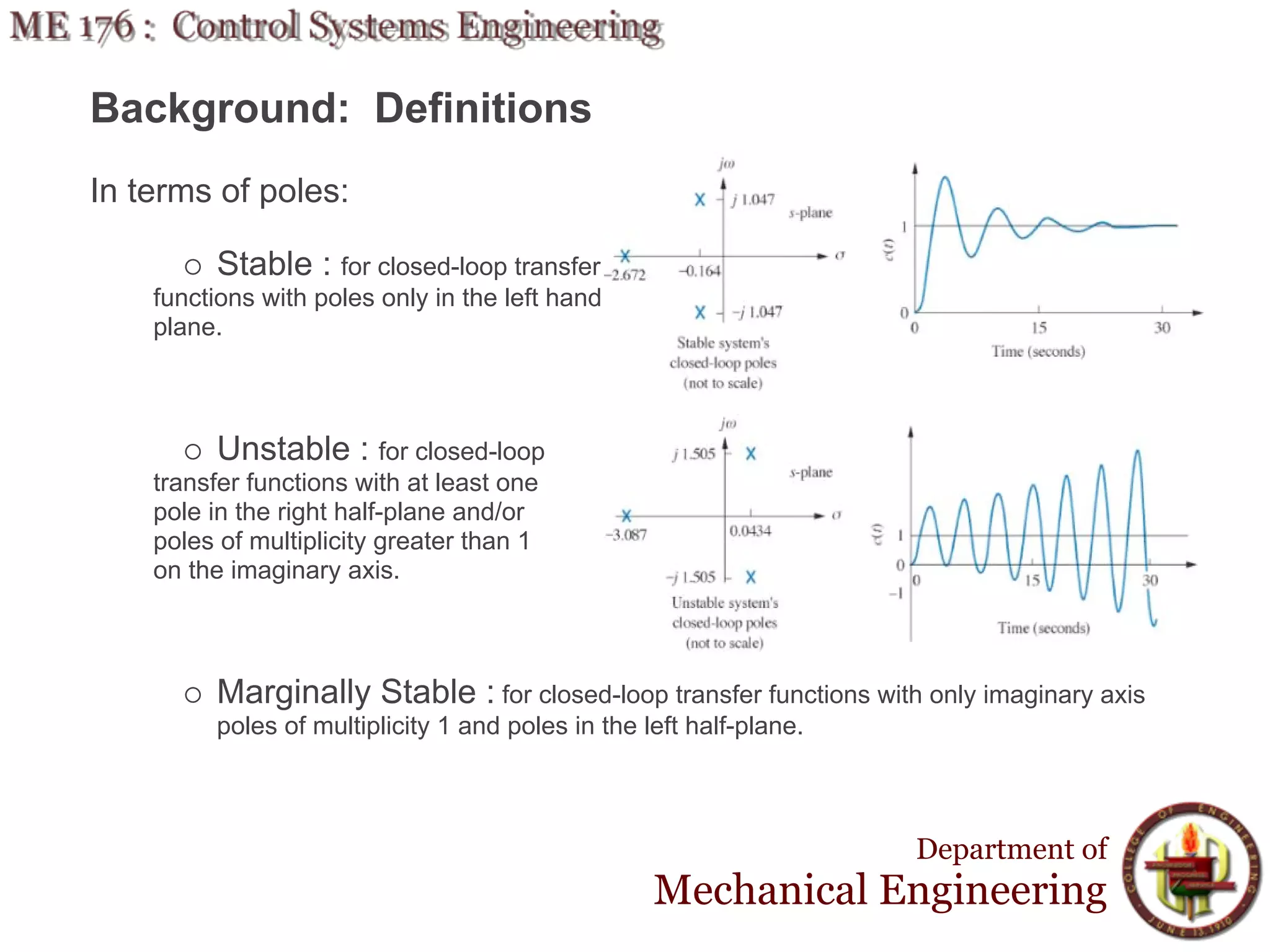
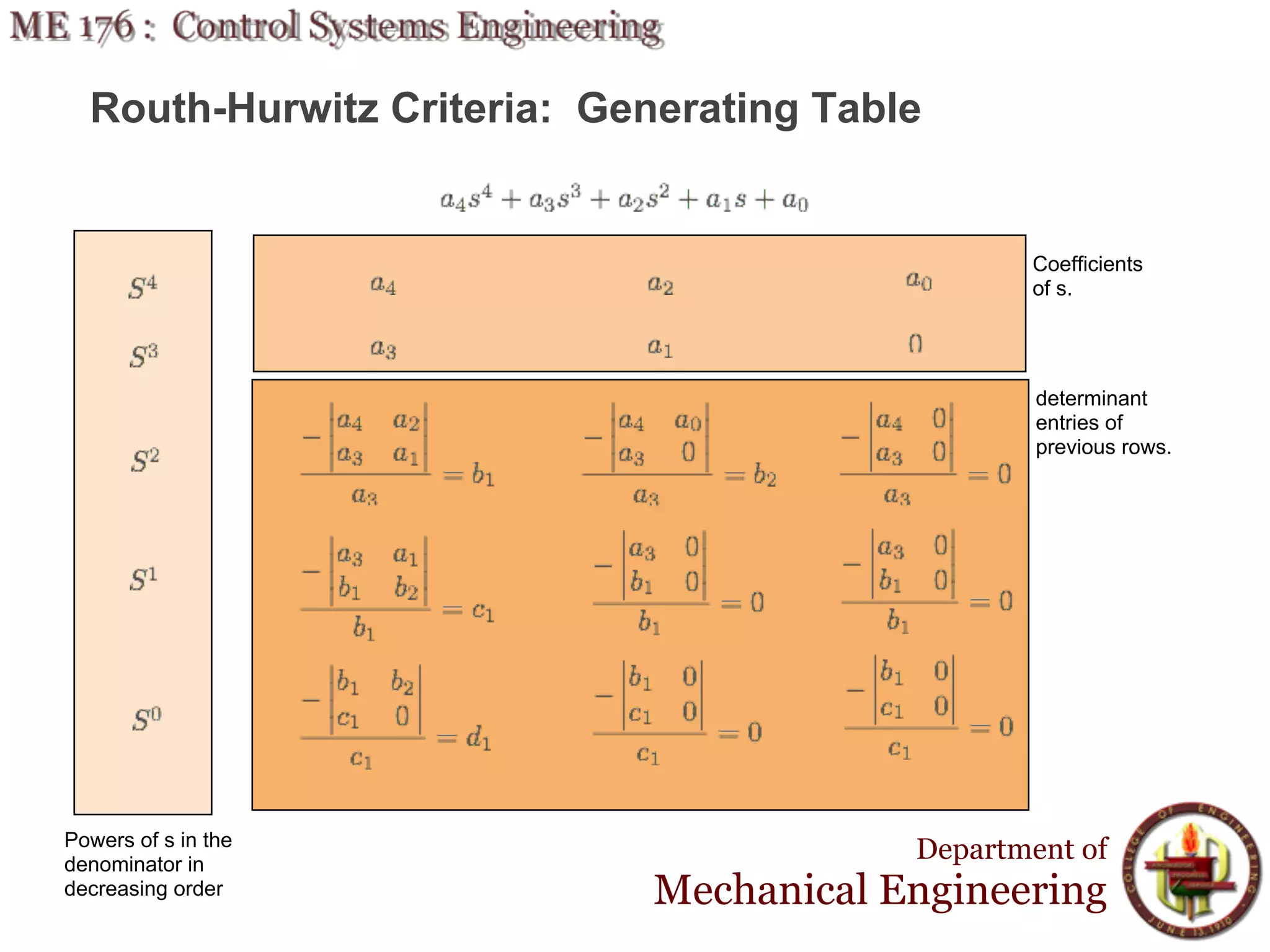
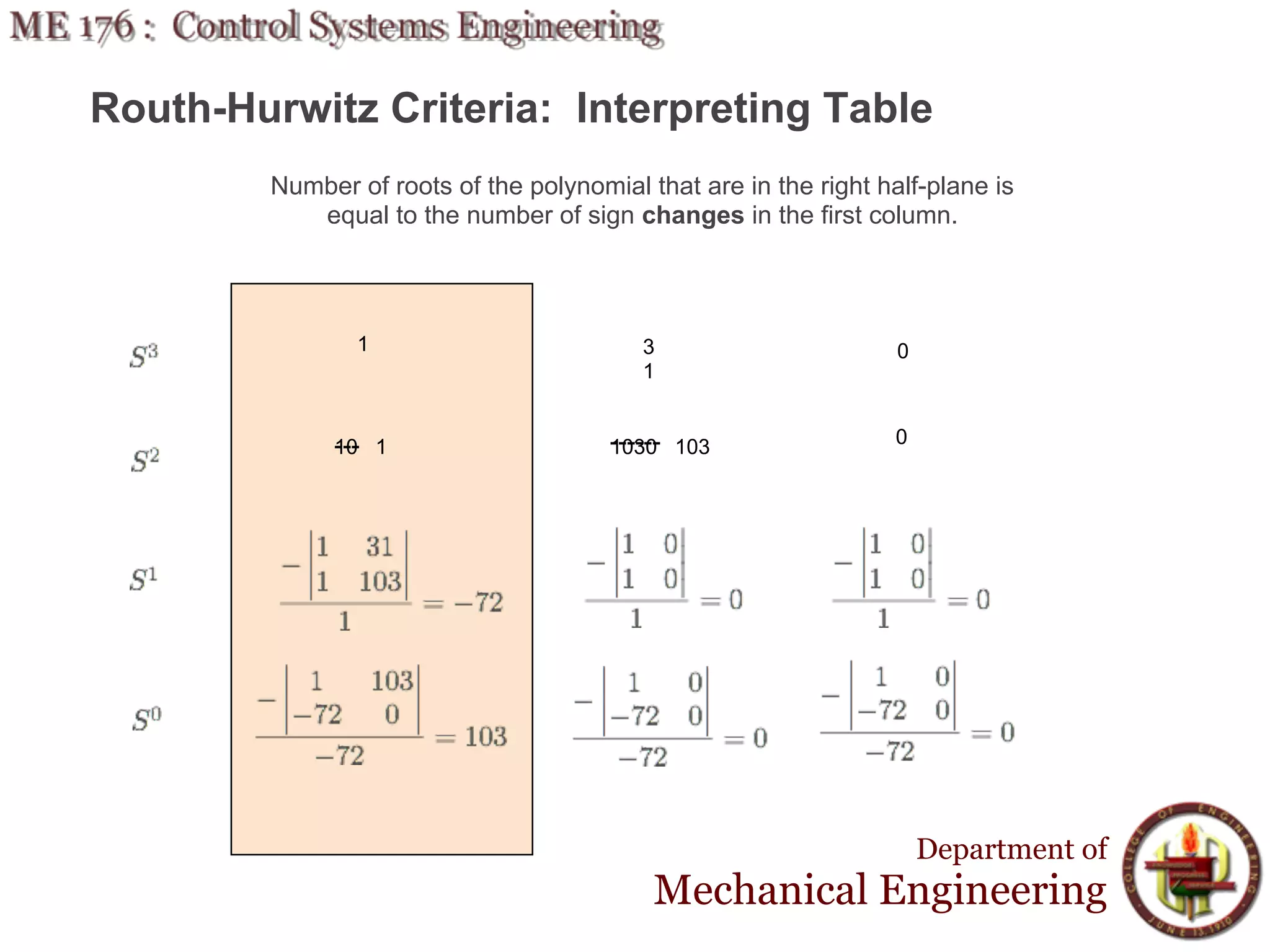
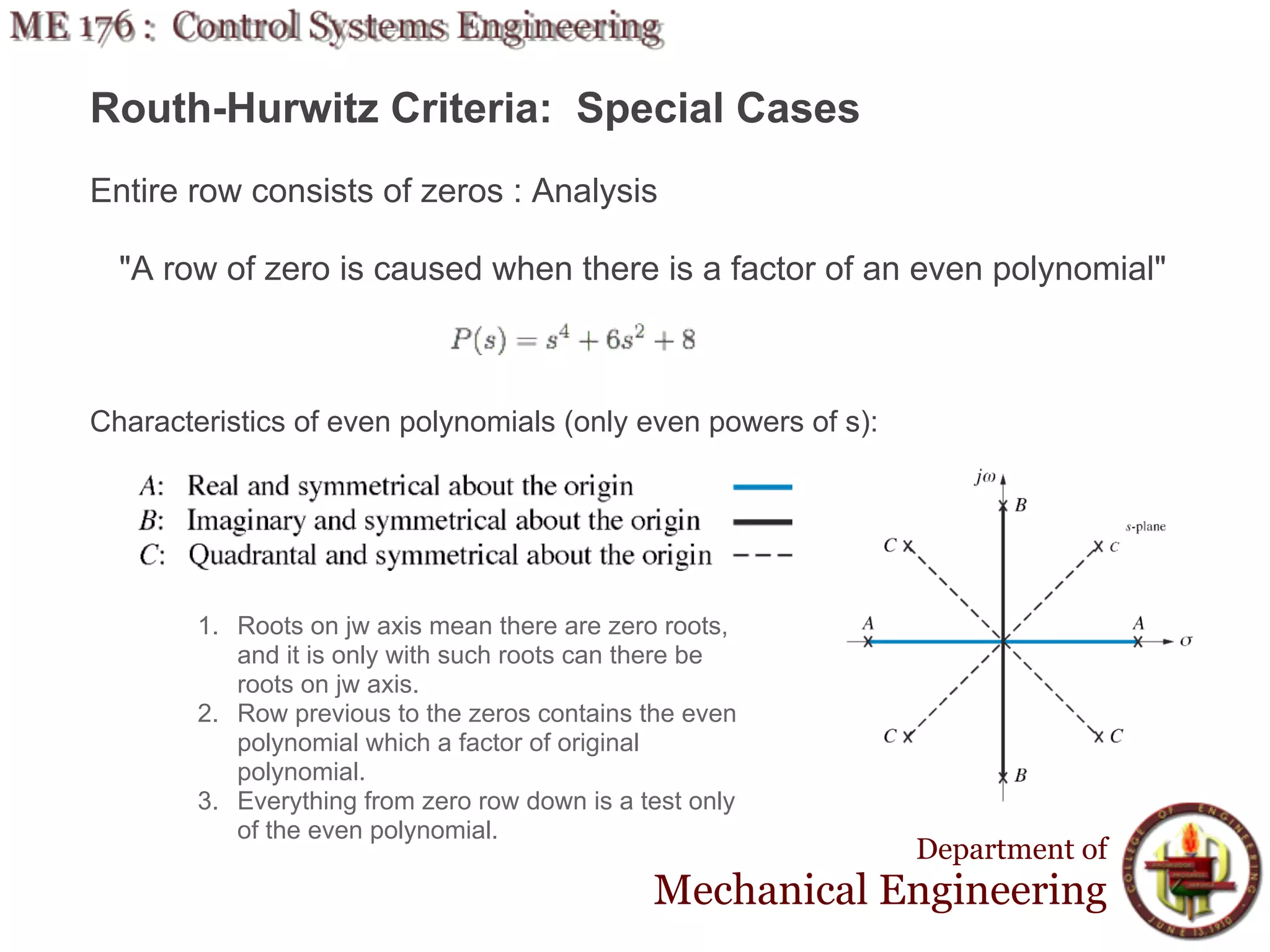
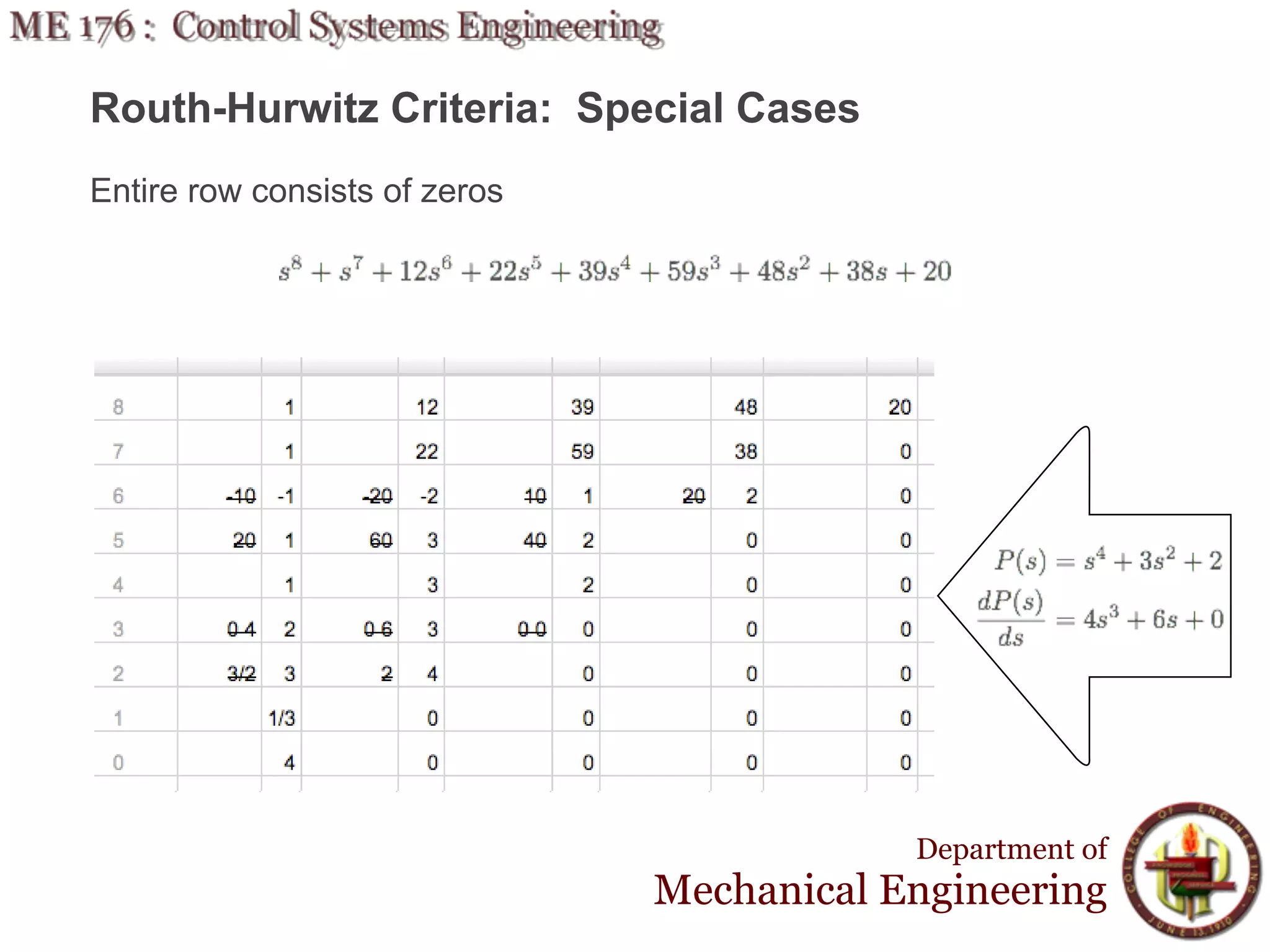
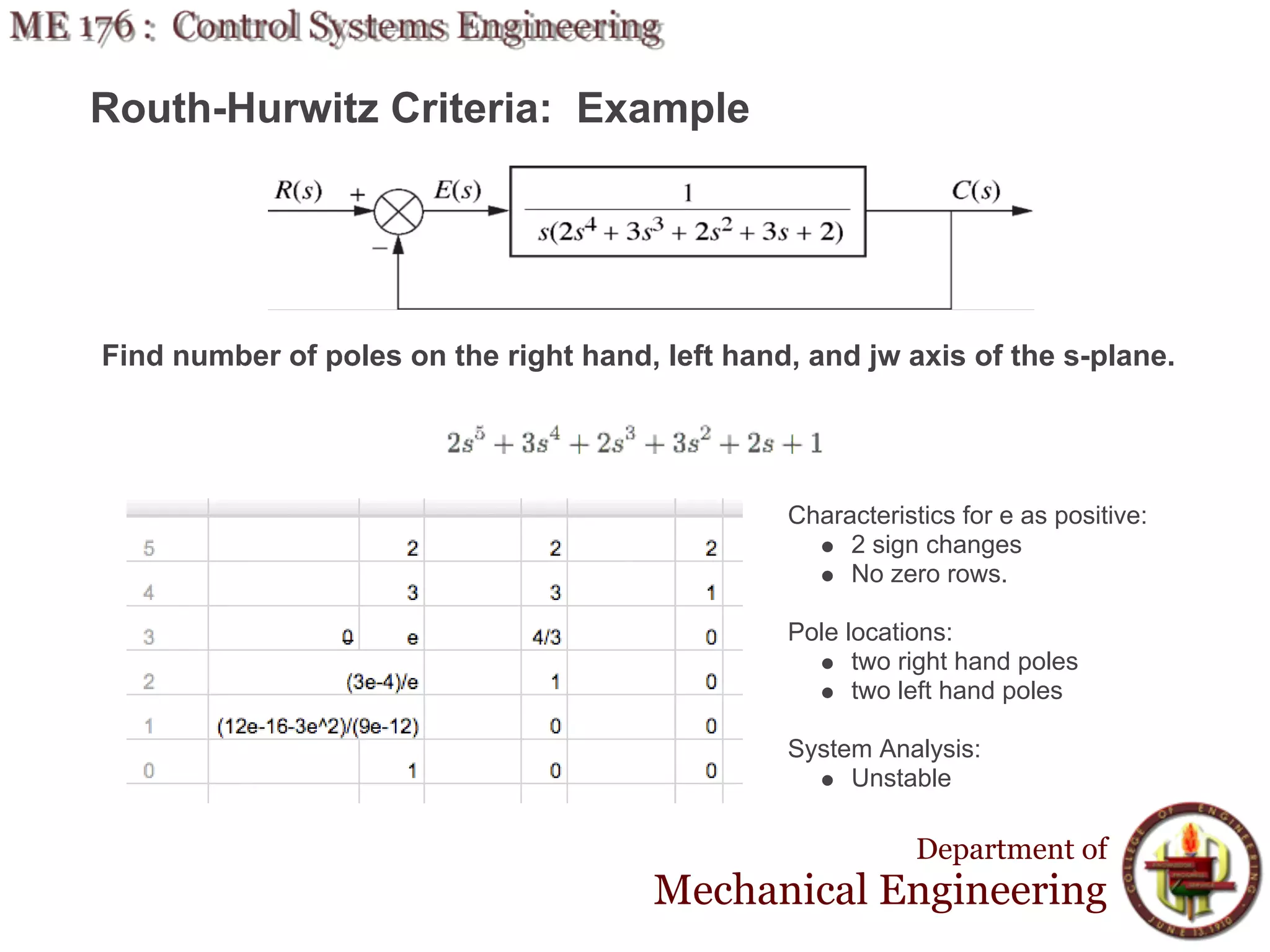
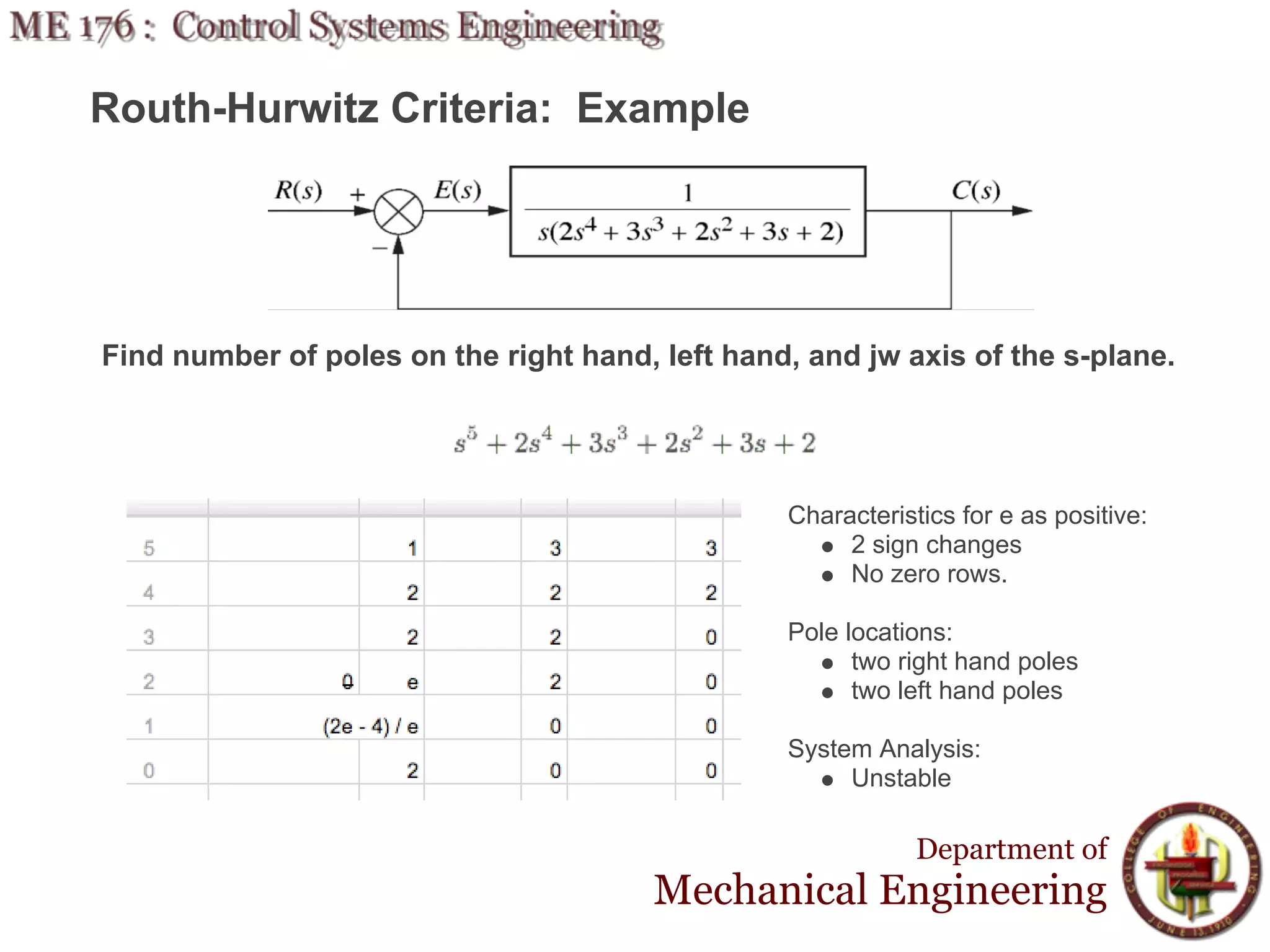
This document discusses stability analysis and design of control systems using the Routh-Hurwitz criteria. It provides definitions of stable, unstable, and marginally stable systems and describes how to generate and interpret the Routh table to determine the number and location of poles. The Routh-Hurwitz criteria allows determining stability based on the number of sign changes in the first column of the table and identifying marginally stable systems with poles only on the imaginary axis. Examples are provided to illustrate applying the method to determine stability and finding design parameters that achieve different stability conditions.

1. ME 176
Control Systems Engineering
Stability
Department of
Mechanical Engineering

2. Background: Design Process
Department of
Mechanical Engineering

3. Background: Analysis & Design Objectives
"Analysis is the process by which a system's performance is determined."
"Design is the process by which a systems performance is created or changed."
Transient Response
Steady State Response
Stability
Department of
Mechanical Engineering

4. Background: Stability
Characteristic : most important system requirement.
Scope :
Linear - the relationship between the input and the output of the
system satisfies the superposition property. If the input to the
system is the sum of two component signals:
In general:
If, then,
Department of
Mechanical Engineering

5. Background: Stability
Characteristic : most important system requirement.
Scope :
Time invariant systems - are systems that can be modeled with a
transfer function that is not a function of time except expressed
by the input and output.
"Meaning, that whether we apply an input to the system now or T
seconds from now, the output will be identical, except for a time delay
of the T seconds. If the output due to input x (t ) is y (t ), then the output
due to input x (t − T ) is y (t − T ). More specifically, an input affected by
a time delay should effect a corresponding time delay in the output,
hence time-invariant."
Department of
Mechanical Engineering

6. Background: Definitions
In terms of natural response:
Stable : natural response approaches 0 as time approaches infinity.
Unstable : natural response grows within bounds as time approaches infinity.
Marginally Stable : natural response neither decays nor grows but remains
constant or oscillates as time approaches infinity.
In terms of total response:
Stable : if every bounded input yields a bounded output.
Unstable : if any bounded input yields an unbounded output.
Department of
Mechanical Engineering

7. Background: Definitions
In terms of poles:
Stable : for closed-loop transfer
functions with poles only in the left hand
plane.
Unstable : for closed-loop
transfer functions with at least one
pole in the right half-plane and/or
poles of multiplicity greater than 1
on the imaginary axis.
Marginally Stable : for closed-loop transfer functions with only imaginary axis
poles of multiplicity 1 and poles in the left half-plane.
Department of
Mechanical Engineering

8. Routh-Hurwitz Criteria:
A method which allows one to tell how many closed-loops system poles are in the
left half-plane, in the right half-plane, and on the imaginary axis.
Steps:
1. Generate the data table, called a Routh table.
2. Interpret the Routh table, to tell how where poles are located.
Power of method is not in the analysis, but in the design. For unknown parameters,
it allows for a closed form expression for the range of the unknown parameters.
Department of
Mechanical Engineering

9. Routh-Hurwitz Criteria: Generating Table
Coefficients
of s.
determinant
entries of
previous rows.
Powers of s in the
denominator in
Department of
decreasing order Mechanical Engineering

10. Routh-Hurwitz Criteria: Generating Table
1 3 0
1
---
10 1 ------ 103
1030 0
Department of
Mechanical Engineering

11. Routh-Hurwitz Criteria: Interpreting Table
Number of roots of the polynomial that are in the right half-plane is
equal to the number of sign changes in the first column.
1 3 0
1
---
10 1 ------ 103
1030 0
Department of
Mechanical Engineering

12. Routh-Hurwitz Criteria: Special Cases
Having zero only in the
first column of the row
(epsilon method)
Positive Negative
1 3 5 + +
2 6 3 + +
7/2 0 + -
3 0 - +
0 0 + +
3 0 0 + +
Department of
Mechanical Engineering

13. Routh-Hurwitz Criteria: Special Cases
Having zero only in the
first column of the row
(reciprocal method)
Positive Negative
3 6 2 + +
5 3 1 + +
4.2 1.4 0 + -
1.33 1 0 - +
-1.7 0 0 + +
5
1 0 0 + +
Department of
Mechanical Engineering

14. Routh-Hurwitz Criteria: Special Cases
Entire row consists of zeros
1 6 8
-- 1
7 -- 6
42 -- 8
56
- - -
--- 4 1
0 -- ---12 3
0 -- --- 0 0
0 --
3 8 0
1/3 0 0
8 0 0
Department of
Mechanical Engineering

15. Routh-Hurwitz Criteria: Special Cases
Entire row consists of zeros : Analysis
"A row of zero is caused when there is a factor of an even polynomial"
Characteristics of even polynomials (only even powers of s):
1. Roots on jw axis mean there are zero roots,
and it is only with such roots can there be
roots on jw axis.
2. Row previous to the zeros contains the even
polynomial which a factor of original
polynomial.
3. Everything from zero row down is a test only
of the even polynomial.
Department of
Mechanical Engineering

16. Routh-Hurwitz Criteria: Special Cases
Entire row consists of zeros
Department of
Mechanical Engineering

17. Routh-Hurwitz Criteria: Example
Find number of poles on the right hand, left hand, and jw axis of the s-plane.
Characteristics:
2 sign changes.
No zero rows.
Pole locations:
two right hand poles
two left hand poles
System Analysis:
Unstable
Department of
Mechanical Engineering

18. Routh-Hurwitz Criteria: Example
Find number of poles on the right hand, left hand, and jw axis of the s-plane.
Characteristics for e as positive:
2 sign changes
No zero rows.
Pole locations:
two right hand poles
two left hand poles
System Analysis:
Unstable
Department of
Mechanical Engineering

19. Routh-Hurwitz Criteria: Example
Find number of poles on the right hand, left hand, and jw axis of the s-plane.
Characteristics for e as positive:
2 sign changes
No zero rows.
Pole locations:
two right hand poles
two left hand poles
System Analysis:
Unstable
Department of
Mechanical Engineering

20. Routh-Hurwitz Criteria: Example
Find number of poles on the right hand, left hand, and jw axis of the s-plane.
Characteristics:
Zero rows at power 5.
Sign change after power 5.
Pole locations:
two right hand poles
four left hand poles
2 at jw axis
System Analysis:
Unstable
Department of
Mechanical Engineering

21. Routh-Hurwitz Criteria: Design
Find K, that will cause the system to be stable, unstable, marginally stable.
case K=1386
Characteristics:
K<1386 : Stable
K>1386 : Unstable
K = 1386 : Marginally Stable
Department of
Mechanical Engineering