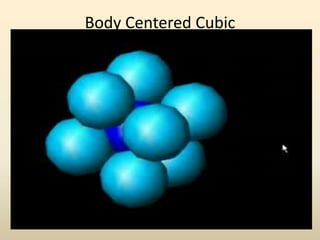
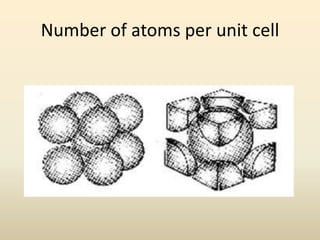
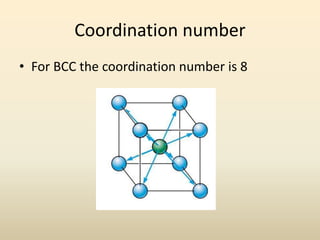
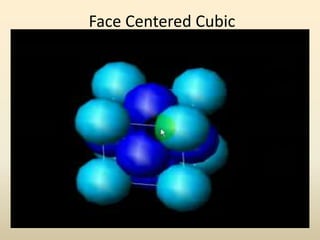
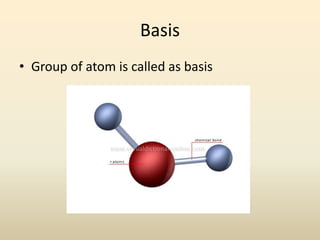
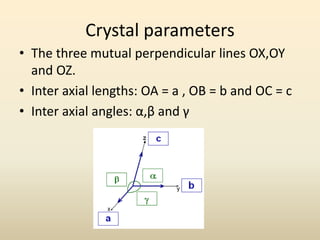
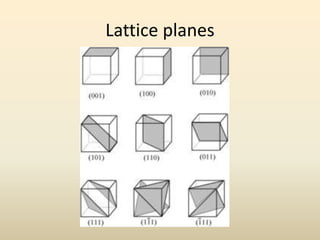
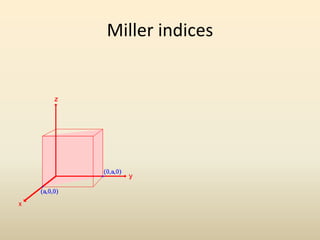
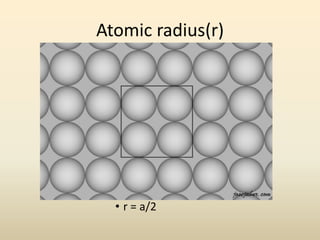
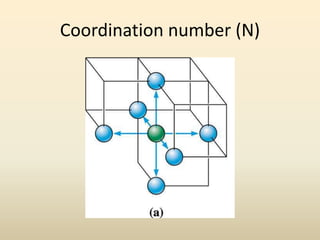
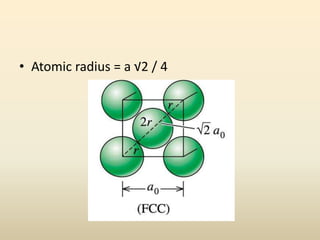
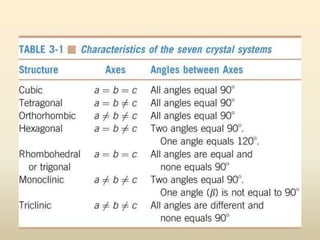
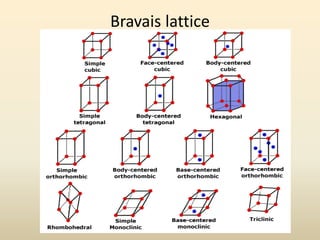
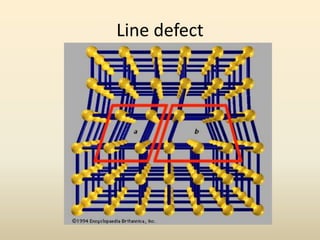
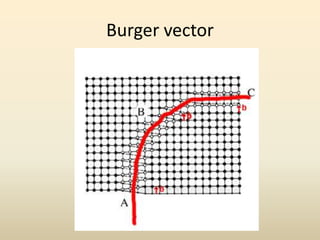
This document discusses key concepts in crystallography including: - Crystal structure is defined as a lattice plus a basis, where a lattice is a periodic arrangement of points in 3D and a basis is a group of atoms. - A unit cell is the smallest repeating geometric shape that defines the lattice, and crystal parameters describe the lengths and angles of the unit cell axes. - There are 7 main crystal systems that describe the symmetry and geometry of unit cells. Crystal defects include point defects like vacancies or interstitials, line defects like dislocations, and surface defects like grain boundaries.

2. Lattice
• Regular , periodical arrangements of points in
three dimension.
• Lattice point : The points which presents in
the lattice

3. Basis
• Group of atom is called as basis

4. Crystal structure
• Lattice + basis = crystal structure
• Crystal structure is obtained by arranging the
basis in each and every lattice point

5. Unit cell
• Smallest geometric figure , by the repetition of
this we get complete crystal structure.

6. Crystal parameters
• The three mutual perpendicular lines OX,OY
and OZ.
• Inter axial lengths: OA = a , OB = b and OC = c
• Inter axial angles: α,β and γ

7. Crystal system
Cubic
Orthorhombic
Monoclinic
Triclinic
Hexagonal
Rhombohedral
Tetragonal

9. Bravais lattice

10. Lattice planes

11. Miller indices

12. d spacing in cubic lattice
d
a
h2  k 2  l 2

13. Calculation of number of atoms
per unit cell – Atomic radius –
Coordination number – Packing
factor for SC , BCC ,FCC and HCP

14. Simple Cubic structure

15. Atomic radius(r)
• r = a/2

16. Coordination number (N)

17. Body Centered Cubic

18. Number of atoms per unit cell

19. Coordination number
• For BCC the coordination number is 8

20. Face Centered Cubic

21. • Atomic radius = a √2 / 4

22. HCP

23. Na Cl structure

24. ZnS Structure

25. diamond and graphite Structure

27. Polymorphism and allotropy
• Polymorphism is a physical phenomenon where
a material may have more than one crystal
structure.
• A material that shows polymorphism exists in
more than one type of space lattice in the solid
state. If the change in structure is reversible,
then the polymorphic change is known as
allotropy.
• The prevailing crystal structure depends on both
the temperature and the external pressure.

28. • Allotropes of carbon
Diamond and graphite

29. Crystal defects
•
•
•
•
Point defect
line defect
surface defect
Burger vector

30. Point defect

31. Line defect

32. Burger vector

33. Dislocations

34. Surface defects
•
•
•
•
Grain boundary
Tilt boundary
Twin boundaries
Stacking fault

35. Thank you for your patience