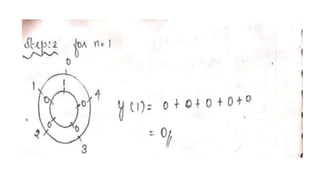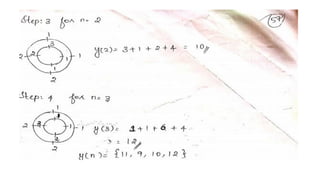The document provides a recap of a webinar focused on discrete time system analysis, covering topics such as linear and circular convolution. Various methods for convolution, including graphical, tabulation, matrix multiplication, and concentric circle methods, are explained along with example problems. The document concludes with quiz questions related to the material discussed.

1. WEBINAR ON DISCRETE TIME SYSTEM
ANALYSIS
Day 5 – 24/7/2020
1
K.Vijay Anand - Associate Professor
Department of Electronics and Instrumentation Engineering
R.M.K Engineering College

2. Recap:
SOLUTION OF DIFFERENCE EQUATION

3. Agenda
Convolution :
Linear Convolution
 Circular Convolution

4. CONVOLUTION

5. DIFFERENCE BETWEEN LINEAR AND CIRCULAR
LINEAR CONVOLUTION
If x(n) have L number of samples
the h(n) have M number of
samples the result y(n)wil have
N=L+M-1 number of samples.
CIRCULAR CONVOLUTON
If x(n) have L number of samples
the h(n) have M number of
samples the result y(n)wil have
N=MAX[L,M] number of samples

6. CONVOLUTION
• LINEAR CONVOLUTION
• CIRCULAR CONVOLUTION

7. LINEAR CONVOLUTION
• GRAPHICAL METHOD
• TABULATION METHOD
• MATRIX MULTIPLICATION METHOD

26. Problem 1
• Determine the output response y(n)=(1,1,1) & x(n)=(1,2,3,1)

30. CIRCULAR CONVOLUTION
• CONCENTRIC CIRCLE METHOD
• MATRIX MULTIPLICATION METHOD

31. STEPS INVOLVED IN CONCENTRIC CIRCLE METHOD
STEP 1 : ARRANGE THE VALUES OF X (N) ANTICLOCKWISE DIRECTON IN OUTER CRCLE
STEP 2 : ARRANGE VALUE OF H (N) IN CLOCKWISE DIRECCTION IN INNER CIRCLE
STEP 3 : MULTIPLY IN CORRESPODING VALUES AND ALL THE ADD VALUES
STEP 4 : IF THE VALUES OF N IS POSITIVE ROTATE IN INNER CIRCLE IN ANTICOCKWISE DIRECTION AND REPEAT STEP 3
STEP 5: REPEAT STEP 4 UNTIL ALL THE ELEMENT ARE ARRANGED AS IN THE INITIAL STEP

32. STEPSINVOLVED IN MATRIX MULTIPICATION METHOD
• ARRANGE THE VALES OF X1(N)& X2(N) IN MATRIX FORMS OF
FOLLOWS

33. • IN THE ABOVE REPRENTATON X2(N) IS ROTATED CIRCULARLY AND IT IS
REPRESENTED IN NXN FORM
• X1 (N) IS REPRESENTED IN COLUMN MATRIX FORM
• WHEN THE BOTH OF THESE X1(N ) AND X2(N) ARE MULTIPLIED,X3(N)
CAN BE OBTANED COLUMN MATRIX FORM

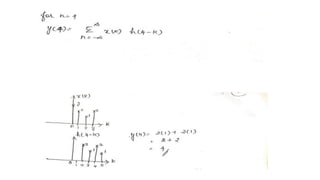
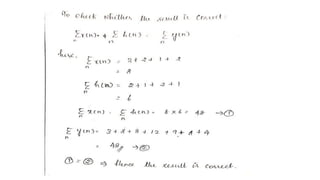
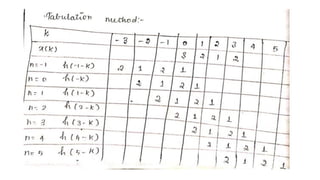
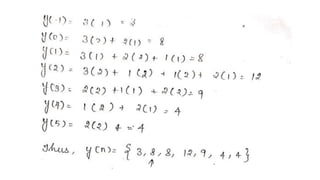
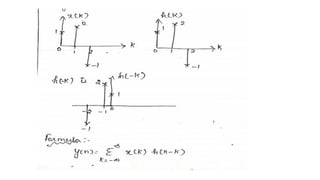
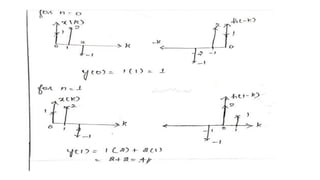
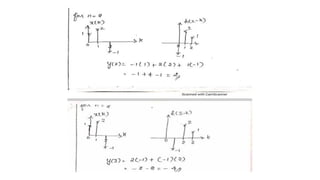
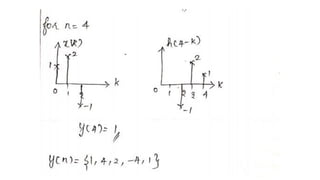
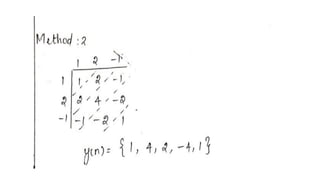
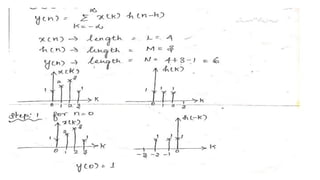
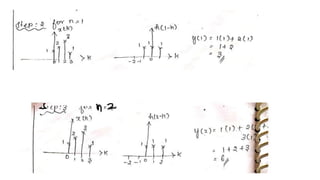
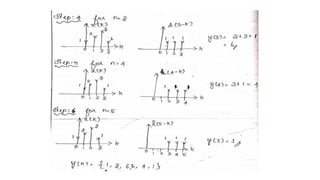
34. PROBLEM 1
FIND THE CIRCULAR CONVOLUTION OF TWO FINITE DURATION SEQUENCES
X1(n)={1,-1,-2,3,-1} X2(n)={1,2,3}
SOLUTION
GIVEN DATA X1(n)={1,-1,-2,3,-1} AND X2(n)={1,2,3}
THE LENGTH OF X1(n)=5
THE LENGTH OF X2(n)=3
THE LENGTH OF X3(n)=MAX[5,3] =5
SO TWO ZEROS WILL BE APPENDED TO THE X2(n) SEQUENCE
• (IE) NEW X2(N)={1,2,3,0,0}

40. PROBLEM 2
• FIND THE CIRCULAR CONVOLUTON OF THE TWO SEQUENCES
X1(N)={1,2,2,1} AND X2(N)={1,2,3,1} BY USING
• CONCENTRIC CIRCLE METHOD
• MATRIX METHOD
SOLUTION
GIVEN DATA X1(N)={1,2,2,1} X2(N)={1,2,3,1}
CONCENTRIC CIRCLE METHOD
HERE VALUE OF N =4 SINCE LENGTH OF M L=4
STEP 1 ARRANGE THE ELEMENT OF X1(N)&X2(N)

44. X1(N)={1,2,2,1} X2(N)={1,2,3,1}

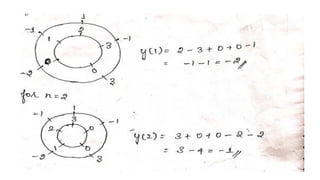
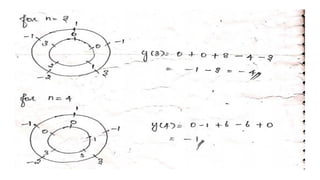
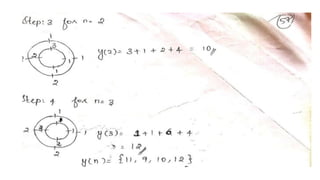
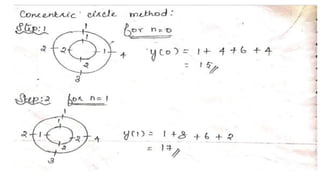
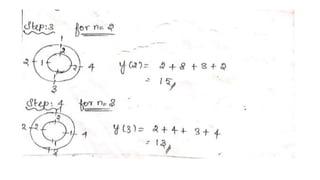
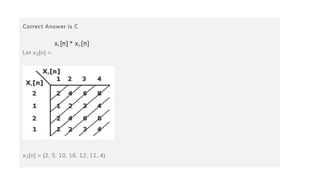
45. PROBLEM :
• GIVEN SEQUENCES X1(N) ={1,2,3,4};X2(N)={1,1,2,2,} FIND X3(N) SUCH
THAT X3(K)=X1(k).X2(K)
• SOLUTION
• X3(N)=IDFT[X3(K)] = IDFT[X1(k).X2(K)
= X1 (N) N X2 (N)
DO CIRCULAR CONVOLUTION TO FIND X3 (N)
X1 (N) ={1,2,3,4}
x2 (N) ={1,1,2,2}

49. PROBLEM
• CONSIDER THE SEQUENCES X1(N)={0,1,2,3,4}
X2(N)={0,1,0,0}.DETERMINE A SEQUENCES Y(N) SO THAT
Y(K)=X1(K).X2(K)
• SOLUTION
• USING CIRCULAR CONVOLUTION THE VALUE OF Y(n) CAN FOUND
OUT BY USING X1(N)&X2(N)

54. QUIZ QUESTIONS

60. THANK YOU