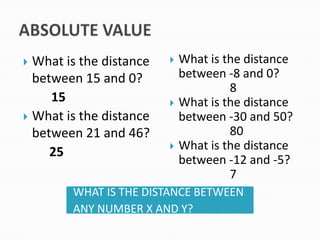
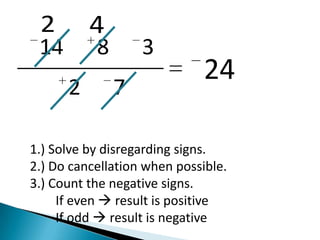
This document provides a summary of key concepts in math including: 1) How to calculate the distance between two numbers by taking the absolute value of their difference. 2) Rules for adding, subtracting, multiplying, and dividing signed numbers. 3) How to simplify algebraic expressions by combining like terms. 4) Laws of exponents and how to evaluate expressions involving exponents. 5) Techniques for multiplying binomial expressions including the distributive property, FOIL method, and column format.

1. Math, Session 2
TIU College Entrance Test Review

2.  What is the distance  What is the distance
between 15 and 0? between -8 and 0?
8
15  What is the distance
 What is the distance between -30 and 50?
between 21 and 46? 80
 What is the distance
25
between -12 and -5?
7
WHAT IS THE DISTANCE BETWEEN
ANY NUMBER X AND Y?

3.  |9|= 9
 | -4 | = 4
 Absolute value is the same number, in positive
form.
 What is the distance between 15 and 0?
Is it | 15 – 0| or | 0 – 15| ?
15 0 0 15
15 15
15 15

4. Distance = | X – Y | = | Y – X |
 What is the distance between -8 and 0?
Answer: | -8 -0 | or | 0 - -8 |
8 0 0 8
8 0 8
8 8
8

5. 7 5 12 9 6 15
Rule for addition of signed numbers of the same
sign: Add the numbers and prefix the common sign.
8 9 1 25 17 8
Rule for addition of signed numbers of different
signs: Subtract the numbers and prefix the
Sign of the number with the larger value.

6. 4 8 4 13 8 5
Rule for subtraction of signed numbers:
Change the operation to addition, and change
The sign of the second number.
Then perform as in addition of signed numbers.

7. 42 121
7 6 11
11
8 4 32 63
7
9
Rule for two numbers with the same sign:
The product/quotient of the two will be positive.

8. 56
4 9 36 7
8
 The rule for two numbers of different signs:
The product/quotient of the two will be
negative.

9. 2 4
14 8 3
24
2 7
1.) Solve by disregarding signs.
2.) Do cancellation when possible.
3.) Count the negative signs.
If even  result is positive
If odd  result is negative

10. 3! 3 2 1
In general,
n! n (n 1) (n 2) (n 3)... 1
Therefore,
5! =?
5! 5 4 3 2 1
120

11. Math, Session 2, Algebra

12.  Evaluate the following expression for x = 4:
2
x 2x 1
2
4 2 4 1
16 8 1
23

13.  We can only add or subtract like terms.
x x 2x
5y 2y 3y
3w 2 x 4w 9 x w 11x
Is the answer 11x –w also correct?
YES!

14. 2
3ab 5a 6ab 2b 9a 4b
 We can only add/subtract like terms.
The simplified form of the AE above is:
2
3ab 2b 14a 4b

15.  We use the laws of exponents.
5
y y y y y y
 Some examples:
2
x x x
2 3 5
x x x x x x x x
2 3
2 2 2 6
x x x x x

16. 7
x x x x x x x x 4
3
x
x x x x
0
x 1
2 1
x 2
x

17.  Master multiplication of simple terms
3 2 5
3x 5x 15x
 3 techniques to multiply (x+a)(x+b)
◦ Distributive Property of Multiplication over
Addition
◦ F-O-I-L Method
◦ Column Format

18.  Technique 1: DPMA
x 2 x 3 x 2 x x 2 3
2
x 2x 3x 6
2
x 5x 6

19. x 2 x 3
First x2
2
Outer 3x x 5x 6
Inner 2x
Last 6 Answer

20. x 2
x 3
3x 6
2
x 2 x ___
2
x 5x 6

21.  Youcan use DPMA and the Column
Format to multiply not only
binomials, but also trinomials and AE’s
with many terms.