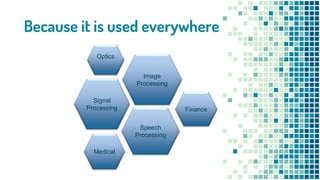
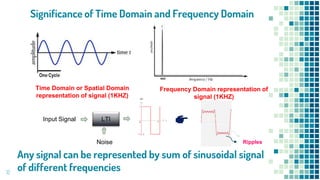
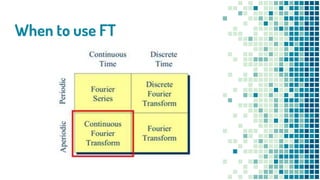
This document discusses Fourier transforms and their applications. It begins by introducing Fourier transforms and noting that they are used widely in optics, image processing, speech processing, and medical signal processing. 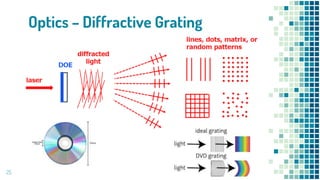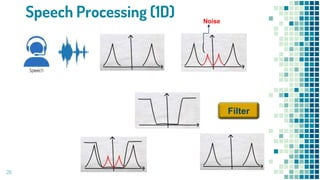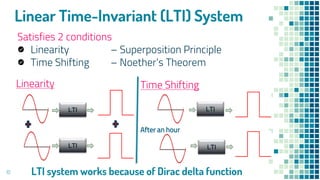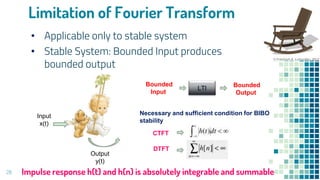It then covers key topics such as: - When periodic and aperiodic signals can be represented by Fourier series versus Fourier transforms - Properties of continuous-time and discrete-time Fourier transforms - Applications of Fourier transforms in filtering ECG signals, modeling diffractive gratings in optics, speech processing, and image processing - Limitations of Fourier transforms in representing non-stable systems The document provides an overview of Fourier transforms and their significance in decomposing signals into constituent frequencies, as well as examples of where they are applied in

1. Nimitha N
Assistant Professor/ECE/RMKCET
nimithaece@rmkcet.ac.in
Hello!

2. FOURIER
TRANSFORM &
ITS
APPLICATIONS
Fourier is just awesome!

3. Guess???
3
Fourier
Transform
Aperiodic
Transform
When
to use
Where to
apply!!!
Signal System Fourier Series FS Properties &
applications

4. Because it is used everywhere
Optics
Image
Processing
Speech
Processing
Medical
Signal
Processing Finance

5. When to use FT

6. 6
Let’s Start with this…
Classification in Periodic Phenomenon
Periodicity in time (Phenomenon comes to you)
• Use Frequency
• Fix the Position of object
Periodicity in space (You goes to Phenomenon)
• Use Period
• Fix the time and measure how the pattern is
distributed in space
Fourier Analysis is associated with symmetry

7. 1807, Periodic signal could be
represented by sinusoidal series
Why sinusoidal?
They are orthogonal.
The shape of the signal will not vary, when
used in LTI System.
They are smooth
Has finite power
Violates none of our criteria for real-world
signals.

8. Periodic Aperiodic
8
Not all phenomenon are periodic.
Aperiodic deals with long period T ∞
 A signal that repeats
its pattern over a
period
 can be represented by
a mathematical
equation
 Deterministic signals
 Power signals
Eg: Pendulum activity
 A signal that doesn’t
repeats its pattern
over a period
 cannot be represented
by a mathematical
equation
 Random signals
 Energy Signals
Eg: Chaotic signal

9. 9
Why can’t we use Fourier series for
Aperiodic signal?
 Fourier Series (FS) exists only for periodic signals.
 Fourier Transform (FT) is derived from FS, i.e. FT is the
envelope of the FS. Hence, the frequency domain becomes
more finer for a aperiodic signal.
Moreover, being able to express a periodic signal as a discrete sum of frequencies is a
stronger statement than expressing it as a continuous sum via the inversion formula.
Representing Aperiodic signal over finite interval -> loss of
information

10. 10
Linear Time-Invariant (LTI) System
Satisfies 2 conditions
Linearity – Superposition Principle
Time Shifting – Noether’s Theorem
LTI system works because of Dirac delta function
Linearity Time Shifting
After an hour
LTI
LTI
LTI
LTI

11. Fourier Transform
11
Transformation of signal from Time domain to
Frequency domain

12. Significance of Time Domain and Frequency Domain
12
Any signal can be represented by sum of sinusoidal signal
of different frequencies
Time Domain or Spatial Domain
representation of signal (1KHZ)
Frequency Domain representation of
signal (1KHZ)
LTI
Noise
Input Signal
Ripples

13. Here it goes…
13
Fourier Analysis is a part of Linear System
Mixed Frequency Signal

14. F.T Analysis : Break the signal or functions into simpler
constituent parts
F.T Synthesis : Reassemble a signal from its
constituent parts
Both Procedures are accomplished by linear operation
(Integral and Series)
14
Fourier transform Procedures
Fourier Analysis is a part of Linear System

15. Continuous Time FT
Magnitude : Determines the contribution of
each component
Phase : Determines which components
are present

16. Discrete Time FT
• Representation of the sequence in terms of
the complex exponential sequence 𝑒𝑗𝜔𝑛
𝐹(ω) = 𝑛=−∞
∞ 𝑓(𝑛) 𝑒−𝑗𝜔𝑛
𝐹 𝜔 = 𝐹𝑟𝑒(ω) + j 𝐹𝑖𝑚𝑔(ω)
Where,
Magnitude, |F(ω)| 2=|Fre(ω)| 2+|Fimg(ω)| 2
Phase , θ(ω) = arg F(ω)

17. Dirichlet’s Condition for existence of FT
The signal should have
• Finite number of maxima and minima over any
finite interval
• Finite number of discontinuities over any finite
interval
• Absolutely integrable
17 Its only a sufficient condition not necessary

18. Properties of FT
▪ http://fourier.eng.hmc.edu/e101/lectures/hand
out3/node2.html
▪ https://www.tutorialspoint.com/signals_and_s
ystems/fourier_transforms_properties.htm
18
If
and

19. Properties of CTFT
Linearity
Time Shifting
Frequency Shifting
Time Reversal
Time Scaling
Differentiation
Convolution
19
Consider, If
and
Helps to turn differential
equation into algebraic
equation

20. Properties of CTFT
▪ Linearity:
▪ Time Shifting:
▪ Frequency Shifting:
20

21. Properties of CTFT
▪ Time Scaling:
▪ Time Reversal:
▪ Differentiation
21

22. Properties of CTFT
▪ Integration:
▪ Multiplication:
▪ Convolution:
22

23. Applications
Speech and
Image Processing
23
Medical Optics

24. Filtering - ECG Signal Analysis
24
https://www.slideserve.com/Thomas/fourier-transform-
and-applications
ECG MACHINE ECG SIGNAL

25. Optics – Diffractive Grating
25

26. Speech Processing (1D)
26
Filter
Noise

27. 27
Image Processing (2D)
Fourier transformation exists always for digital images as
they are limited and have finite number of discontinuities.

28. Limitation of Fourier Transform
• Applicable only to stable system
• Stable System: Bounded Input produces
bounded output
28
Input
x(t)
Output
y(t)
LTI
Bounded
Output
Bounded
Input
CTFT
DTFT
Necessary and sufficient condition for BIBO
stability
Impulse response h(t) and h(n) is absolutely integrable and summable

29. “
29

30. Thank you!
Please write your
questions in comments
…Happy to clarify your
doubts
30