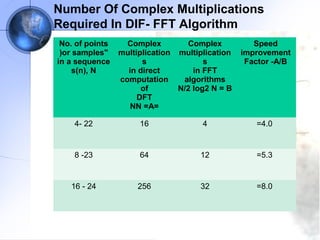
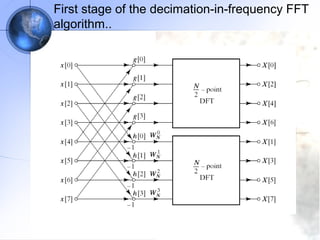
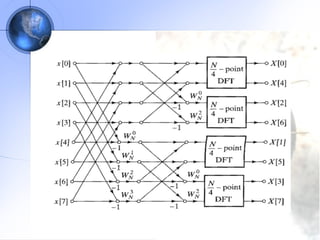
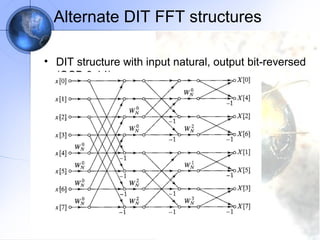
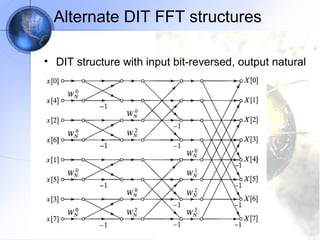
This document discusses fast Fourier transform (FFT) algorithms. It provides an overview of FFTs and how they are more efficient than direct computation of the discrete Fourier transform (DFT). It describes decimation-in-time and decimation-in-frequency FFT algorithms and how they exploit properties of the DFT. The document also gives an example of calculating an 8-point DFT using the radix-2 decimation-in-frequency algorithm.

1. DIF-FFT
Presented by :
Aleem Alsanbani
Saleem Almaqashi

2. Fast Fourier Transform FFT
- A fast Fourier transform (FFT) is an efficient algorithm to compute
the discrete Fourier transform (DFT) and inverse of DFT.
- There are many FFT algorithms which involves a wide range of
mathematics,. A Discrete Fourier transform decomposes a
sequence of values into components of different frequencies.
- This operation is very useful in many fields but computing it
directly from the definition is often too slow to be practical .

3. Cont ..
• FFT are special algorithms for speedier implementation of DFT.
• FFT requires a smaller number of arithmetic operations such
as multiplications and additions than DFT.
• FFT also requires lesser computational time than DFT .

4. Fast Fourier Transform Algorithms
• Direct computation of the DFT is less efficient because it does
not exploit the properties of symmetry and periodicity of the
phase factor WN = e-j2π/N .
• These properties are:
- Symmetry property.
- Periodicity property.
• As we already know that all computationally efficient algorithms
for DFT are collectively known as FFT Algorithms and these
algorithms exploit the above two properties of phase factor, WN.

5. FFT Algorithms Classification Based On
Decimation
• Another classification of FFT algorithms based on Decimation of
s(n) :r S(K). Decimation means decomposition into decimal
parts. On the basis of decimation process, FFT algorithms are
of two types:
• 1. Decimation-in-Time FFT algorithms.
• 2. Decimation-in-Frequency FFT algorithms.

6. Cont..
• Decimation-in-Time Algorithms: sequence s(n) will be broken
up into odd numbered and even numbered subsequences.
• This algorithm was first proposed by Cooley and Tukey in 1965.
• Decimation-in-Frequency Algorithms. the sequence s(n) will
be. Broken up into two equal halves.
• This algorithm was first proposed by Gentlemen and Sande in
1966.
• Computation reduction factor of FFT algorithms .
• Number of computations required for direct DFT / Number of
computations required for FFT algorithm
• = N2 / N / 2 log2 (N)

7. decimation-in-frequency FFT algorithm
• In decimation-in-frequency FFT algorithm, the output DFT
sequence S(K) is broken into smaller and smaller
subsequences. For the derivation of this algorithm, the number
of points or samples in a given sequence should be N = 2r
where r > 0. For this purpose, we can first-divide the input
sequence into the first-half and the second-half of the points.
• Flow graph of complete decimation-in-frequency (DIF)
decomposition of an N-point DFT computation (N = 8).

8. Steps for Computation of Decimation in Frequency
FFT Algorithm
• Given below are the important steps for the computation of DIF
FFT algorithms.
• 1. Data shuffling is not required but whole sequence is divided
in two parts: first half and second half. From these we calculate
g(n) and h(n) as follows:
• g(n) = s(n) +s(n+N/2 )
• and h(n) = s(n)-s(n+N/2 )
• where n = 0, 1, ..., N/2 -1
Finally data shuffling is performed. It is also performed by Bit
reversal.

9. Number Of Complex Multiplications Required In
DIF- FFT Algorithm
• Number of complex multiplications required in decimation-m-.
FFT algorithm are the same as that required in decimation-in-
time FFT algorithm.
• Number of complex multiplication required in these DFT
algorithms are N/2 log2iV, where N= 2r, r>0 and N is the total
number of points (or samples) in a discrete-time sequence.
Thus the total computations (number of multiplication and
addition operations) are the same in both FFT algorithms.
• Now we will compare the computational complexity for the direct
computation of the DFT and FFT algorithm. This comparison is
given in Table

10. Number Of Complex Multiplications
Required In DIF- FFT Algorithm
No. of points Complex Complex Speed
(or samples" multiplication multiplication improvement
in a sequence s s Factor -A/B
s(n(, N in direct in FFT
computation algorithms
of N/2 log2 N = B
DFT
NN =A=
4- 22 16 4 =4.0
8 -23 64 12 =5.3
16 - 24 256 32 =8.0

11. First stage of the decimation-in-frequency FFT
algorithm..

13. Alternate DIT FFT structures
• DIT structure with input natural, output bit-reversed
(OSB 9.14):

14. Alternate DIT FFT structures
• DIT structure with input bit-reversed, output natural

15. Radix-2 Decimation-In-Frequency Solved
Example Part1
• Example Find the DFT of the following discrete-time
sequence .
• s(n) = {1, -1, -1, -1, 1, 1, 1, -1} using
Radix-2 decimation-in-frequency FFT algorithm.
• Solution. The Twiddle factor or phase rotation factor
WN= involved in the FFT calculation are found out as
follows for N= 8.

16. Example Part1

17. Example Part1

18. Radix-2 decimation-in-frequency Solved
Example Part2
• Fig.Flow graph of Radix-2 decimation-in-frequency (DIF) FFT
algorithm N = 8. In Radix-2 decimation-in-frequency (DIF) FFT
algorithm, original sequence s(n) is decomposed into two
subsequences as first half and second half of a sequence.
There is no need of reordering (shuffling) the original sequence
as in Radix-2 decimation-in-time (DIT) FFT algorithm. But
resultant discrete frequency sequence is shuffled (reordered)
into natural order because these are obtained in unnatural
order. Flow graph of Radix-2 decimation-in-frequency (DIF) FFT
algorithm for N= 8 is shown in Fig. Determination of DFT using
Radix-2 DIF FFT algorithm requires three stages because the
number of points in a given sequence is 8, i.e., = 2r — N — 8,
where r is number of stages required = 3.

19. Solv.
Stage I :
A0 = s(0) + s(4) = 1 + 1 = 2
A1 = s(l) + s(5) = -1 + 1 =0
A2 = s(2) + s(6) = -1 + 1 = 0
A3 = s(3) + s(7) = -1 - 1 = -2
A4 = [s(0)+(-1) s(4)] W80 = [1 + (-1) (1)] x 1 =0
A5 = [s(1) + (-1) s(5)]W81 = [-1 + (-1)(1)]((1-j) /√2= - √2(l - j)
A6 = [s(2) + (-1) s(6)]W82 = [-1 + (-1) x 1] (- j) =2j
A7 = [s(3) + (-1) s(7)]W83 = [-1 + (-1)(-1)]{(-(1-j) /√2} = 0

20. Solv….
S(K) = {S(0), S(l), S(2), S(3), S(4), S(5), S(6), S(6),
S(7)}
Or S(X) = {0-√2+(2 + √2 )j, 2 -2j √2+(-2 + √2)j,4,
√2+ (2 - √2 )j,2 + 2j,- √2 -(2 + √2)7}

21. Conclusions
• Radix 22, 24… Structure uses less adders and
multipliers but still has good efficiency processing
DIF DFT
• Common Factor Algorithm and Butterfly Structure
enable this architecture to reuse its modules
numerous times

22. References
• [1],Shousheng He and Torkelson, M. “A new approach to pipeline FFT
processor,” Proceedings of IPPS '96, 15-19, pp766 –770. April 1996
• [2] Alan V.Oppenheim, Ronald W. Schafer, “ Discrete-time signal
processing “ 2nd edition
• [3] Zhangde Wang “INDEX MAPPING FOR ONE TO MULTI
DIMENSIONS “Electronics Letters Publication Volume: 25, pp: 781-782 Jun
1989
• [4] He, S. & Torkelson, M., A systolic array implementation of common
factor algorithm to compute DFT, Proc. Int. Symp. on Parallel Architectures,
Algorithms and Networks, Kanazawa, Japan, pp. 374-381, 1994.
• [5]IJung-YeolOH and Myoung-Seob LIM , ‘Fast Fourier Transform Algorithm
for Low-Power and Area-Efficient
Implementation’EICETRANS.COMMUN.,VOL.E89–B, APRI
• [6]BURRUS, c. s.: 'Index mappings for multidimensional formulation
of the DFT and convolution',IEEE Trans., 1977, ASSP-25, (6), pp. 239-242

23. _________
_____
__