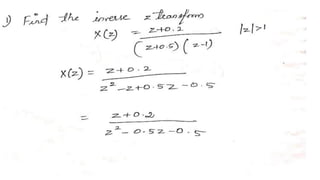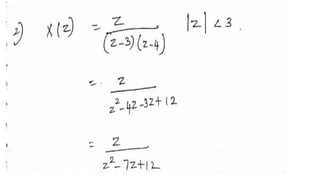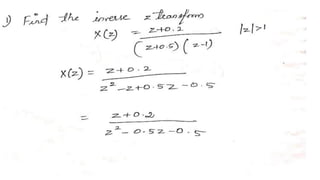
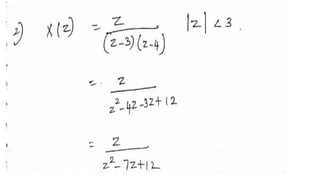
The document outlines a webinar focused on discrete time system analysis, detailing key properties of the Z-transform, including linearity, time shifting, and convolution properties. It discusses methods for inverse Z-transform, such as long division, partial fraction, and Cauchy’s integration methods. Additionally, it covers the initial and final value theorems for discrete time sequences.

1. WEBINAR ON DISCRETE TIME SYSTEM
ANALYSIS
Day 3 – 22/7/2020
1
K.Vijay Anand - Associate Professor
Department of Electronics and Instrumentation Engineering
R.M.K Engineering College

2. Properties of Z transform
• Linearity Property
• Time Shifting Property
• Multiplication by Exponential
Sequence Property
• Time Reversal Property
• Differentiation in Z-Domain OR
Multiplication by n Property
• Convolution Property
• Conjugation property
• Intial Value theorem
• Final Value theorem

4. X(z)
z
Lt
x(n)
0n
Lt
x(0)




INITIAL VALUE THEOREM:
Let x(n) be a discrete time causal sequence and ZT[ x(n) ] = X(z),
then according to initial value theorem of z transform
7/28/2020 4

9. Inverse z-transform
 Long Division Method or synthetic Division
 Partial Fraction Method
 Cauchy’s Integration Method
 Solution of difference Equation
9

17. Partial Fraction Method

24. CAUCHY RESIDUE THEOREM

25. Residue Method

26. Cauchy Residue Theorem