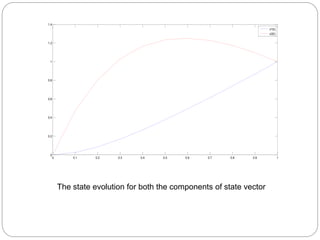
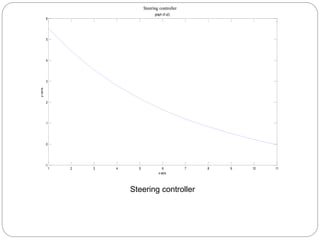
The document discusses linear dynamical systems and controllability of linear systems. It defines dynamical systems as mathematical models describing the temporal evolution of a system. Linear dynamical systems are ones where the evaluation functions are linear. Controllability refers to the ability to steer a system from any initial state to any final state using input controls. The document provides the definition of controllability for linear time-variant systems using the controllability Gramian matrix. It also gives the formula for the minimum-norm control input that can steer the system between any two states. An example of checking controllability for a time-invariant linear system is presented.

1. Dr. Purnima K. Pandit
Department of Applied Mathematics,
Faculty of Technology and Engineering,
The M. S. University of Baroda,
Kalabhavan,
Vadodara-390001
Controllability
of
Linear Dynamical System

2. Outline
 Introduction
 Dynamical Systems
 Controllability of Linear Systems

3. Introduction - Dynamical Systems
 Any physical phenomena whose state changes over time can be
mathematically modelled as dynamical systems. It is simply a
model describing the temporal evolution of a system.
 Dynamical systems are mathematical objects used to model physical
phenomena whose state changes over time.
 Examples of the dynamical system are the swinging of a clock
pendulum, the flow of water in a pipe and the number of fish each
spring time in a lake.
 The general form of dynamical system is
 
 
.
0 0
,X f X t
X t X



4.  A dynamical system can be classified as follows:
(1) Linear dynamical system
In this system evaluation functions are linear.
(2) Non-linear dynamical system
In this system evaluation functions are not linear.
(3) Time variant system
System whose output depends explicitly on time or if it’s
characteristics change with time.
(4)Time invariant system
System whose output does not depend explicitly on time or if it’s
characteristics change with time.

5. (5) Discrete time system
The state variable representing the current state of discrete time system
(digital) is where is discrete point at which system is being
evaluated. The discrete time state equations are
which describe the next state of system
with respect to current state and inputs of system.
(6) Continuous time system
The state variable representing the current state of a continuous time
system (analog) is and the continuous time state equations are
which describe the next state of system with respect to current state
and inputs of system.
 x n
 1 [ ] [ ]x n Ax n Bu n  
  1x n
[ ]u n
 x t
 
   
dx t
Ax t Bu t
dt
 
 dx t
dt

6. Existence and Uniqueness
 Consider the initial value problem
where, f is some arbitrary function defined and continuous in some
neighbourhood.
 Theorem : A function is a solution of the initial value problem
(2.1) on an interval if and only if it is a solution of an integral
equation
0 0' ( , ( )), ( ) (2.1)x f t x t x t x 
0
0( ) ( , ( ))
t
t
x t x f s x s ds  

7. Lipschitz Condition
Gronwalls Inequality
2
1 2 1
A function ( , ) defined in a region is said to satisfy a Lipschitz
condition w.r.t in if there exists a positive constant such that
| ( , ) ( , ) | |
f t x D R
x D k
f t x f t x k x

  
   
2
1 2
|
for every , and , . 0 is called the Lipschitz constant.
x
t x t x k 
0
0
0
Let ( ) and ( ) be two non-negative continuous functions for .Let
be any non negative constant. Then the inequality
( ) ( ) ( ) ,
implies the
t
t
f t g t t t k
f t k g s f s ds t t

  
0
0
inequality ( ) exp ( ) ,
t
f t k g s ds t t 

8. Picard’s Theorem
 0 0
i) Let ( , ) be a continuous real valued real valued function defined on
the closed rectangle
( , ):| | , | | , , 0
and let | ( , ) | ( , )
ii) Let ( , ) satisfy Li
f t x
R t x t t a x x b a b
f t x M t x R
f t x
     
  
0
1 2 1 2
1 2
0 0 1 0
pschitz condition | ( , ) ( , ) | | |
( , ) and ( , ) in with Lipschitz constant then the successive
approximations ( ) , ( ) ( , ( )) converge in the interval
|
t
n n
t
f t x f t x k x x
t x t x R x k
x t x x t x f t x s ds
I t t

  
 
  
 

0
'
0 0 0
| min , to a unique solution ( ) of the IVP
( ) ( , ), ( ) on .
b
h a x t
M
x t f t x x t x I
 
   
 
 

9. System of Differential Equations
0 0
The solution of the above system is given as
Consider the initial value problem
( ) ( ), ( ) ,
be a non singular matrix
x t Ax t x t x t I
A n n
  

&
   
0
1
0 0
0
0
0
The matrix ( , ) called as the state transition matrix can be defined as follows:
( , ) (t) ( ) , in (- , ).
Here, ( ) is th
,x t t t x
t t
t t t t t
t

 


 
   

matrix formed by the linearly independent solutions
o
e fundamental
f the system.
HOMOGENEOUS:

10. Calculation of fundamental matrix
1
Case 1: For different and real eigen values
6 5
Let
1 2
Eigen values of are =1 and =7 and the corresponding
1 5
eigen vectors are and
Thus the two indep
.
1 1
endent solutions are
( )
A
A
t
 

 
  
 
   
   
   
7
2
7
7
1 5
and ( )
1 1
Therefore, the fundamental matrix is given by
5
( )
t
t t
t
t t
t e
e e
t
e
e e


   
   
   
 
  
 


11. 2
1
Case 2: For real repeated eigen values
6 5
Let
1 2
Eigen values of are =2 and =2.
1
For =2 the corresponding eigen vector is given by
1
1
1
Thus the two independent solutions are
( ) t
t
A
e
A




 
  
 
 
 

 



2
2
2 2
2 2
1
and ( )
1
Therefore, the fundamental matrix is given by
( )
t
t t
t t
t te
e te
t
e te


  
  
  
 
  
 

12. Case 3: For complex eigen values
1 1
Let
1 1
Eigen values of are =1 and =1 .
For =1 the corresponding eigen vector is given by
1
For =1+ the corresponding eigen vector is given by
A
A i i
i
i
i
 


 
  
 
 
 
  
 
 
 
1
1
=
1 1
cos sin
= cos sin =
1 cos sin
sin
Thus the solutions can be computed as
( )
=
cos
t it
t t
t
i t
i
i i
e e
i i t t
e t i t e
t i t
t
e
e
t
t  
 
 
 
   
   
   
   
    


  


cos
sin
t
i
t
   
    
   

13.    
 
1 2
Thus the two independent solutions are
sin cos
and
cos sin
Hence the fundamental matrix is given by
sin cos
cos sin
t t
t t
t t
t t
t e t e
t t
e t e t
t
e t e t
 

   
    
   
 
  
 

14. 0 0
Consider the initial value problem
( ) ( ) , ( ) ,
be a continuous matrix defined on a closed and bounded interval I.
The solution of the abo
x t Ax t B x t x t I
A n n
   

&
     
0
0 0
ve system is given as
, ,
t
o
t
x t t t x t Bd   
 
  
  

NONHOMOGENEOUS:

15. Controllability
 In the world of control engineering, there are large amount of
systems available that need to be controlled.
 The task of a control engineer is to design controller and
compensator units to interact with this pre-existing systems.
 A dynamical system is said to be completely controllable, if for
any initial and final states and in the state space X, there
exist control u that will steer the system from
ix Tx
0( ) to ( )i Tx t x x T x 

16.  Consider linear time variant system given as
where A is n dimensional square matrix called evolution matrix and
B is matrix of dimension called as control matrix.
 The system (3.1) is controllable if the controllability Grammian is
invertible.
 The controllability Grammian for (3.1) is given by
 The system is controllable if the rank of the controllability
Grammian is the same as the rank of the evolution matrix:
0 0
( ) ( ) ( ) ( ) ( ) (3.1)
( )
X t A t X t B t u t
X t X
 

&
n p
1
0
0 1 0 0( , ) ( , ) ( ) ( ) ( , )
t
T T
t
W t t t t B t B t t t dt  
( ) ( )rank W n rank A 

17.  The minimum norm steering control for the system (3.1) is given
by
 If A(t) and B(t) are time invariant in system (3.1) then the
controllability Grammian is given by
 And the minimum norm steering control is given by
 1
0 0 1 0 0 1 1( ) ( ) ( , ) ( , ) ( , )T
u t B t t t W t t x t t x 
  
0
0 0 1 1
0 0 0
This control steer the system (3.1) from ( ) to ( ) with the
state evolution given as
( ) ( , ) ( , ) ( )
t
t
x t x x t x
x t t t x t Bu d    
 
 
  
  

1
0 0
0
( ) ( )
0 1( , )
T
t
t t A t t AT
t
W t t e BB e dt 
 
0 0 1( ) ( )1
0 1 0 1( ) ( , )
T
t t A t t AT
u t B e W t t x e x 
    

18.  This controller steers the state from .The state transition for
all t is given by
0 1tox x
0 0
0
( ) ( )
0( ) ( )
t
t t A t A
t
x t e x e Bu d
  
 
  
  


19.  Example of Time Invariant case
.
0 1
1
2
1 2
1 2
1
1 0 1
Consider the equation where and with
0 2 1
0 1
condition and
0 1
1 0
Sol:
0 2
and 2
andt
X AX Bu A B
X X
x
AX
x
dx dx
x x
dt dt
x e x
   
      
   
   
    
   
   
   
  
   
 2
2
2
0 02 2
0
Therefore the fundmental matrix is ( )
0
And the state transition matrix is given by
0 0
( , ) and similarly ( , )
0 0
t
t
t
t t
t t
e
e
t
e
e e
t t t t
e e

 






 
  
 
   
    
   

20.  
0 0
0
1 1
2 2 2 2
0 0
2 2
The controllability Grammian matrix is given by
(0, ) ( , ) ( , )
1 1 10 0 0 0
(0,1) 1 1 =
1 1 10 0 0 0
=
t
T T
t t t t
t t t t
t t
t t
W t t t BB t t dt
e e e e
W dt dt
e e e e
e e
e e
 
          
           
          
 

 

 
11 1 2 3 2 3
2 3 4 3 4
0 0 0
1
1
0
= =
0
3.1945 6.3618
(0,1)
6.3618 13.3995
13.3995 6.36181
(0,1)
6.3618 3.19452.3322
5.7454 2.7278
(0,1) =
2.7278 1.3697
|
t t t t t
t t t t t
e e e e e
dt dt
e e e e e
W
W
W
W


     
     
     
 
  
 
 
  
 
 
 
 
 
(0,1) | =2.3322 0
The system is therefore controllable.


21.  
 
1 1
0 0 1 0 0 1
1
2 2
2
We can find the controller ( ) as follows
( ) ( , ) ( , )[ ( , ) ]
5.7454 2.7278 0 10 0
= 1 1
2.7278 1.3697 0 10 0
5.7454 2.
=
T T
t
t
t t
u t
u t B t t W t t X t t X
e e
e e
e e
 
  
         
          
           

 
 2
2
7278 2.7183
2.7278 1.3697 7.3891
4.5383
=
2.7059
( )= 4.5383 2.7059
t t
t t
e e
u t e e
  
  
   
 
   
 
 

22.  
0 0 0
0
2
2 2
0
2
2
We can find the solution ( ) as follows
( ) ( , )[ ( , ) ]
0 10 0
= 4.5383 2.7059
0 10 0
0 4.5383 2.7059
=
0
t
tt
t
t
t
X t
X t t t X t Bu d
e e
e e d
e e
e e e
e

 


   





 
       
         
        
   
 
 


3
3 4
0
2 3
2 3 4
0
2 3
2 3 4
4.5383 2.7059
0 2.2691 0.9020
=
0 1.5128 0.6765
0 2.2691 0.9020 1.3671
=
0 1.5128 0.6765 0.8363
t
tt
t
t t t
t t t
d
e e
e e e
e e e
e e e
e e e
X

 
 
 





  
  
    
   
  
   
    
  
    

2
2 2
2.2691 0.9020 1.3671
( )=
1.5128 0.6765 0.8363
t t t
t t t
e e e
t
e e e


   
 
   

23. .
0 1
1
2
1 2
1 2 2
2
2
1 0
Consider the equation where and with
0 11
0 1
condition and
0 1
1
Sol:
0 1
and
Now
t
t
t
e
X AX Bu A B
X X
xe
AX
x
dx dx
x x e x
dt dt
dx
dt
x



  
     
  
   
    
   
 
  
  
   
 

1
2 1 2
2
1 1 2 1
2 2 22
1 1 1
2 1
2
21 1
1 12
and
=
= 2 = 2
2 =0 ( 2) 0 ( 2)( 1) 0
1, 2
t t
t t t t
t
dx
x e x x e
dt
d x dx dx dx
x e e x e x e
dt dt dt dt
dx dx dx
x e x
dt dt dt
d x dx
x D D x D D
dt dt
D
 
   

  
     
 
   
 
          
  
• Example of Time Variant Case

24. 2
1 1 2
21
1 2
1
1 2
2 2
1 2 1 2 2
2
2 2
2 2
2
( )
2
Now
2
3
( ) 3
Therefore the fundmental matrix is ( )
0 3
and
t t
t t
t
t t t t t
t t
t
t t
t
x t c e c e
dx
c e c e
dt
dx
x x e
dt
c e c e c e c e x e
c e x e
x t c e
e e
t
e





  
 




  
  
 
    
  
  
 
  
 
0 0
0
2
1
0
1
0 0
31
( )
3 0
And the state transition matrix is given by
( , ) ( ) ( )
t t
t
e e
t
e
t t t t  
 

  
  
  


25. 0 0
0
0 0 0
0
0 0 0
0
22
0
2 2
2 2
2 2
31
( , )
3 0 3 0
31
=
3 0 3
1
( )
= 3
0
1
( )
( , ) 3
0
t tt t
tt
t t t t t t
t t
t t t t t t
t t
t t t
t
e e e e
t t
e e
e e e
e
e e e
e
e e e
t
e
  


 
 

    

    

    

    
    
  
   
  
 
 
   
  
 
 
   

 
21
( )
(0, ) 3
0
e e e
e
  

 
 

 
 
  
 

26.  
0
0 1 0 0
1
0
21
2
0
The controllability Grammian matrix is given by
( , ) ( , ) ( , )
(0,1) (0, ) (0, )
1 10
0( ) (
= 0 1 =3 31
1 ( )0 3
t
T T
t
T T
W t t t t BB t t dt
W BB d
e
e e e e
d
e e ee

   
  

 
    


  



  
     
         
   



21
2
0
4 2 2
21 1
2
2 20 0
0
0 0)
1
0 1 ( )0 3
1 1
1 ( 2 ) ( )0
0 ( ) 9 3
= 3 1
1( )
0 ( )3
3
e
e e
d
e e ee
e e e e ee
e e
d
e e e
e e e e

 
  

    
 
  
   





  



  
    
       
   
 
             
           
 

 
1
4 2 2
2 2
0
1 1
2
9 4 2 3 2
=
1
3 2 2
0.2417 0.8541
(0,1)=
0.8541 3.1945
| (0,1) | 0
System is controllable at 0.
e e e
e e
e e
e
W
W
t
  
 
 


 

    
       
    
  
    
  
 
 
 



27. 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
0
0.2
0.4
0.6
0.8
1
1.2
1.4
x1(t)
x2(t)
The state evolution for both the components of state vector

28. 1 2 3 4 5 6 7 8 9 10 11
-1
0
1
2
3
4
5
6
x-axis
y-axis
graph of u(t)
Steering controller
Steering controllerSteering controller