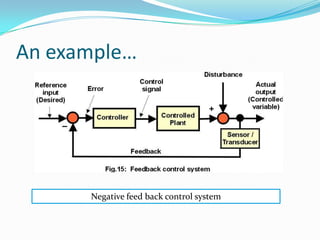
This document discusses control systems and their analysis using state space models. It defines the key components of a control system and explains how state space representation models systems using state variables and matrices. The document also covers analyzing stability, controllability and observability of state space models.

1. Aalok P Bhat(1rv09ec002)
Ganesh V Bhat(1rv09ec027)
Sujith Chandra P S(1rv09ec105)

3. Control system…
 Device or a set of devices that mange, command, direct
or regulate the behavior of other device or system.
 Control system can be thought of as having four
functions; Measure, Compare, Compute, and Correct
 These functions are completed by five
elements: Detector, Transducer, Transmitter,
Controller, and Final Control Element.
 Practically a control system is implemented in
embedded system using a microcontroller or a PLD’s

4. Control theory…
 It is an interdisciplinary branch of engineering and
mathematics that deals with the behavior of
dynamical systems.
 Usual objective of control theory is to calculate
solutions for the proper corrective action from the
controller that result in system stability.
 Transfer function (also known as the system function
or network function) is a mathematical tool to define
the relation between input and the output.

5. Classification…
 Logical or sequential controls
 usually implemented using logic gates(combinational circuit)
 Feedback or linear controls
 Usually implemented using combinational circuit and flip
flops(sequential circuit)
 Fuzzy control
 attempts to combine some of the design simplicity
of logic with the utility of linear control. Some devices or
systems are inherently not controllable.

6. An example…
Negative feed back control system

7. Mathematical approach…
y(s)=p(s)u(s)
u(s)=c(s)e(s)
e(s)=r(s)-f(s)y(s)
C-controller
P-plant
F-sensor
* All the transfer
function(system) are assumed
to by linearly time invariant

8. Analysis and design of a feedback
control system…
Two approaches are available for the analysis and design
of feedback control systems.
 Classical or frequency-domain approach
 Algebraic approach of converting a single input single output
system’s differential equation into transfer function by
transforming the system equation into the frequency domain
equivalent called transfer function.
 State-space approach
 Linear algebraic approach of representing a multiple input
multiple output system into a mathematical model

9. Classical approach…
 It is the frequency domain approach where the
mathematical tools like laplace transforms are applied
 Steps followed in a classical approach:
 System equation (in time domain) is transformed into a
frequency domain transfer function.
 Computation, simplification and analysis is done in
frequency domain.
 The obtained result is transformed back to time domain
using inverse transforms.

10. Advantages:
 they rapidly provide stability and transient response
information
Disadvantage:
 The primary disadvantage of the classical approach is
its limited applicability:
 It can be applied only to linear, time-invariant systems
or systems that can be approximated as such.

11. State-space approach…
 System functions are represented in the form of
matrices instead of a single system equation.
 It is a unified method for modeling, analyzing, and
designing a wide range of systems.
 It can be used to represent nonlinear systems.
 It can handle, conveniently, systems with nonzero
initial conditions.
 The modeling of time-varying system is easy with the
help of state-space approach.

12. STATE SPACE
REPRESENTATION

13. • In control engineering, a state space representation is a
mathematical model of a physical system as a set of input, output
and state variables related by first-order differential equations
• To abstract from the number of inputs, outputs and states,
the variables are expressed as vectors, and the differential
and algebraic equations are written in matrix form

14. • When the complexity of the equation is more, it is very difficult
to work in time domain
• So we decompose the higher-order differential equations into
multiple first-order equations, and we solve them using
state variables method
• State space refers to the space whose axes are the state variables.
The state of the system can be represented as a vector within that space

15. STATE SPACE
• The state-space is the vector space that consists of all the
possible internal states of the system
• In a state space system, the internal state of the system is
explicitly accounted for by an equation known as the
state equation
• The system output is given in terms of a combination of the
current system state, and the current system input, through
the output equation
• These two equations form a system of equations known
collectively as state-space equations

16. STATE
• The state of a system is an explicit account of the values
of the internal system components
STATE VARIABLES
• Input variables : We need to define all the inputs to the
system, and we need to arrange them into a vector, denoted by u(t)
• Output variables : Output variables should be independent of one
another, and only dependent on a linear combination of the input
vector and the state vector and it is denoted by y(t)

17. • State Variables
• State variables are the smallest possible subset of system variables
that can represent the entire state of the system at any given time
•The state variables represent values from inside the system,
that can change over time
• In an electric circuit, for instance, the node voltages or the
mesh currents can be state variables
• State variable is denoted by x(t)

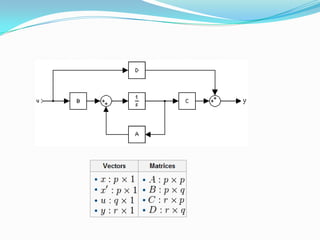
18. State-Space Equations
• In a state-space system representation, we have a system of two equations
• equation for determining the state of the system
x'(t) = g[t0,t,x(t),x(0),u(t)]
• equation for determining the output of the system
y(t) = h[t,x(t),u(t)]
• x‘(t) = A(t)x(t) + Bu(t)
• y(t) = C(t)x(t) + Du(t)

19. Mattrices:A,B,C,D
• Matrix A is the system matrix, and relates how the current state
affects the state change x‘
• Matrix B is the control matrix, and determines how the
system input affects the state change
• Matrix C is the output matrix, and determines the relationship
between the system state and the system output
•Matrix D is the feed-forward matrix, and shows how the system
input to affects the system output directly

21. State-Space Basis Theorem
Any system that can be described by a finite number of
nth order differential equations or nth order difference
equations, or any system that can be approximated by
them, can be described using state-space equations. The
general solutions to the state-space equations, therefore, are
solutions to all such sets of equations

22. Representing Systems By
State Space Approach
 Select a particular subset of all possible system
variables and call it as state variables.
 For an nth-order system, write n simultaneous, first-
order differential equations in terms of the state
variables. We call this system of simultaneous
differential equations state equations.

23.  We algebraically combine the state variables with the
system's input to get output equation.
 State equations and output equations combined form
a state-space representation.

24. Representation of an Electric
Network
Step 1:Identify variables in the system.
Ic,Vc,Il,Vl
Step 2:Select the state variables by writing the
derivative equation for all energy storage elements

25.  Step 3:Represent other variables as linear combination
of state vectors and input.
 Step 4:Obtain State equations.

26.  Step 5:Obtain output equations and represent in
matrix form.

27. Representing
Differential/difference equation in
State Space Model.
 Consider the differential equation
 We choose output y and it’s n-1 derivatives as state
variable.(Phase Variables).

29. Representing Transfer Function to
State Space
 we first convert the transfer function to a differential
equation
 Then we represent the differential equation in state
space in phase variable form.

30. Stability of System
 A linear state space model is asymptotically stable if all
real parts of eigenvalues of A are negative.
 Correspondingly, a time-discrete linear state
space model is asymptotically stable if all
the eigenvalues of A have a modulus smaller than one.

31. Controllability
 state controllability condition implies that it is
possible – by admissible inputs – to steer the states
from any initial value to any final value within some
finite time window.
 A continuous time-invariant linear state-space model
is controllable if and only if

32. Observability
 Observability is a measure for how well internal states
of a system can be inferred by knowledge of its
external outputs.
 A continuous time-invariant linear state-space model
is observable if and only if