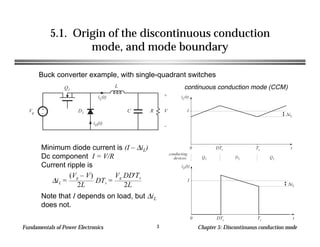
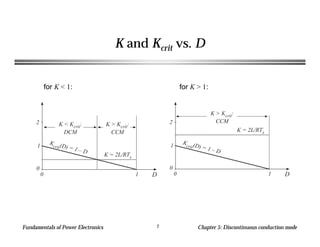
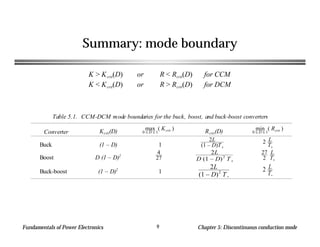
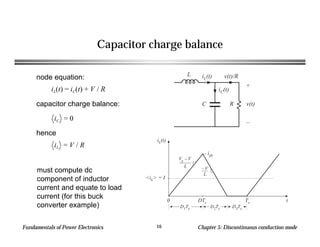
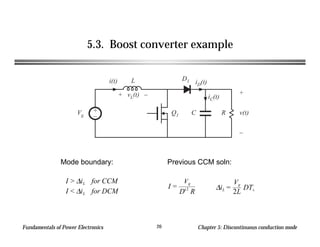
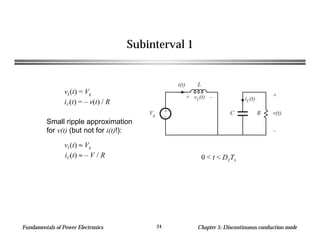
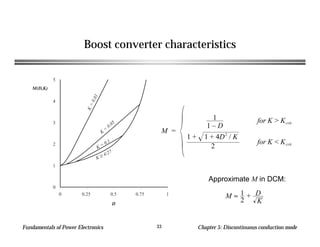
This chapter discusses discontinuous conduction mode (DCM) in power electronics. DCM occurs when inductor current or capacitor voltage ripple causes the applied switch current or voltage to reverse polarity. Analysis techniques for DCM include inductor volt-second balance and capacitor charge balance. The chapter provides an example analysis of a buck converter in DCM and derives the mode boundary and conversion ratio equations.