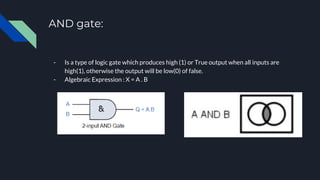
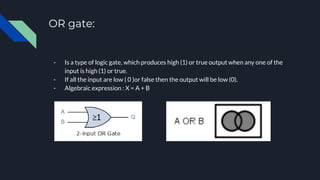
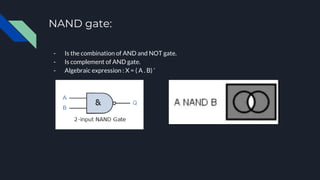
- Boolean algebra is used to analyze and design digital logic circuits and determines logical propositions as either true or false. It uses basic logic gates like AND, OR, and NOT. - AND gates output 1 only if all inputs are 1, while OR gates output 1 if any input is 1. NOT gates invert the input. More complex gates can be made by combining basic gates, like NAND (AND with output inverted) and NOR (OR with output inverted). - Boolean algebra has laws like commutative, distributive, complement, identity, and associative laws that define the operations of logical variables and simplify expressions. Together, Boolean algebra and logic gates form the foundation of digital circuit and computer design.

1. Chapter 4. Logic
Function and
Boolean Algebra

2. Definition:
- Is the algebra of two valued system of logic that determines the logical
prepositions in terms of True or False.
- The logic function and Boolean algebra both are integrated in one to design a logic
circuit of computer or any electronic circuits.

3. Example:
● Proposition : Any True or False declarative sentence is termed as proposition or
statement.
- George Boole was mathematician : True statement
- The Sun rises in the west : False statement
● Negation: When a statement is presented by its contradiction, then that
statement is known as negation statement.
- let statement p = the king is brave then its negation is written as ~p = the king is
not brave.
- if p is true then ~p is false and if p is false then ~p is true.

4. Boolean function:
- Is an expression formed with binary variables, the two binary operators OR and
AND, the unary operator NOT, parenthesis and equal sign.
- Example:
Boolean function F= ( abc ) is equal to 1
If a = 1 AND b = 1 AND c = 1, otherwise F = 0
- Boolean function is represented as an algebraic expression as well as truth table.
A B A.B
0 0 0
0 1 0
1 0 0
1 1 1

5. Boolean operator:
- Is a symbol that performs and indicates any operation between two or more
operands.4
- There basic operators in boolean function:
a. AND operator ( Product operator)
b. OR operator ( Addition operator )
c. NOT operator ( reverse operator )

6. Logic Gate:
- Is an electronic circuit to receive more than one input and deliver single output.
- Gates are often called as logic circuit because they can be analyzed with boolean
algebra.
- The computer system is a set of gates.
- ALU is responsible for mathematical and logical processing of data.
- Three basic gates in digital computer:
a. AND gate
b. OR gate
c. NOT gate

7. AND gate:
- Is a type of logic gate which produces high (1) or True output when all inputs are
high(1), otherwise the output will be low(0) of false.
- Algebraic Expression : X = A . B

8. Truth table of AND gate:
Input Output
A B A.B
0 0 0
0 1 0
1 0 0
1 1 1

9. OR gate:
- Is a type of logic gate, which produces high (1) or true output when any one of the
input is high (1) or true.
- If all the input are low ( 0 )or false then the output will be low (0).
- Algebraic expression : X = A + B

10. Truth table of OR gate:
Input Output
A B A + B
0 0 0
0 1 1
1 0 1
1 1 1

11. NOT gate:
- Is a type of logic gate in which the output will be the complement or just reverse of
input.
- If the input will be low (0) or false then the output will be high (1) or true and vice
versa.
- Algebraic expression : X = A ‘ or A
A

12. Truth table of NOT gate:
Input Output
0 1
1 0

13. Comparison of AND, OR and NOT gate:
AND gate OR gate NOT gate
- Receives more than
one input and
produces only one
output
- Receives more than
one input and
produces only one
output
- Receives only one
input and gives only
one output
- If all signal are high,
the output will be high
- If anyone input signal
is high, the output
signal becomes high.
- It inverts high input
into low and low into
high, so called as
inverter.

14. NAND gate:
- Is the combination of AND and NOT gate.
- Is complement of AND gate.
- Algebraic expression : X = ( A . B) ’

15. Truth table of NAND gate:
Input
X = A . B X = ( A . B ) ‘
A B
0 0 0 1
0 1 0 1
1 0 0 1
1 1 1 0

16. NOR gate:
- Is the combination of OR and NOT gate.
- Is the complement of OR gate.
- Produces high (1) output when all inputs are low (0) otherwise, the output will be
low (0).
- Algebraic expression : X = ( A+B ) ‘

17. Truth table of NOR gate:
Input
X = A + B X = ( A + B ) ‘
A B
0 0 0 1
0 1 1 0
1 0 1 0
1 1 1 0

18. X-OR gate:
- Is exclusive OR gate which produces low (0) output when all the inputs are same
otherwise, the output will be high (1).
- Algebraic expression : X = A ’ . B + A . B ’

19. Truth table of X-OR gate:
Input Output
A B A’ B’ A’.B A.B’ A’.B + A.B’
0 0 1 1 0 0 0
0 1 1 0 1 0 1
1 0 0 1 0 1 1
1 1 0 0 0 0 0

20. X-NOR gate:
- Is exclusive NOR gate.
- Is just the complement of X-NOR gate which produces high (1) output when all the
inputs are either low (0) or high (1).
- Algebraic expression : X = A . B + A ‘ . B ’

21. Truth table of X-NOR gate:
Input Output
A B A’ B’ A’.B’ A.B A.B +
A’.B’
0 0 1 1 1 0 1
0 1 1 0 0 0 0
1 0 0 1 0 0 0
1 1 0 0 0 1 1

22. NAND and NOR gate as universal gate:
- Because these gates are efficient to implement any boolean function.
- The combination of NAND gate can be used to perform AND and NOT operation.
- The combination of NOR gate can be used to perform OR and NOT operation.

23. De-Morgan’s theorem:
● First theorem : “ The complement of sum equals to the product of the
complement.”
● Mathematically : ( A + B ) ‘ = A’ . B’
Input Ouput 1 Output 2
A B A + B ( A +B )’ A’ B’ A’ . B’
0 0 0 1 1 1 1
0 1 1 0 1 0 0
1 0 1 0 0 1 0
1 1 1 0 0 0 0

24. ● Second theorem : “ The complement of a product is equal to the sum of the
complement. ”
● Mathematically: ( A . B ) ‘ = A’ + B’
Input Ouput 1 Output 2
A B A . B ( A . B )’ A’ B’ A’ + B’
0 0 0 1 1 1 1
0 1 1 1 1 0 1
1 0 1 1 0 1 1
1 1 1 0 0 0 0

25. Different laws of Boolean Algebra:
● Commutative law : i) A +B = B + A ii) A . B = B . A
● Distributive law : A . ( B + C ) = A . B + A . C
● Complement law : i) ( A’ ) ‘ = A ii) A . A’ = A
● Identity law : i) A . 0 = 0 ii) A + 0 = A iii) A . 1 = A
iv) A +1 =1
● Associative law : i) A + ( B + C ) = ( A + B) + C ii) A . ( B . C) = (A .
B) . C