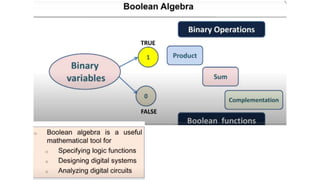
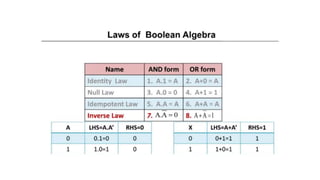
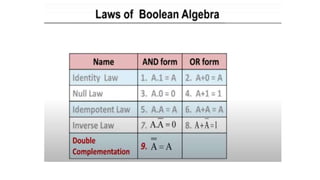
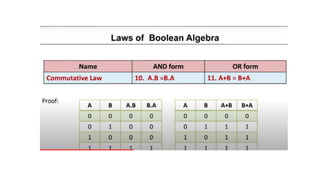
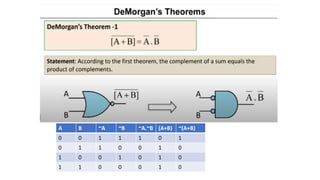
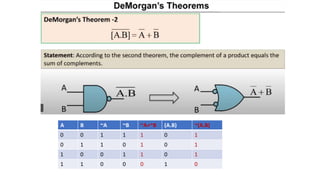
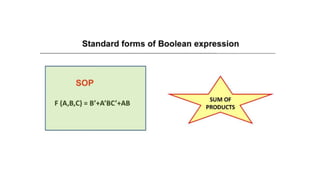
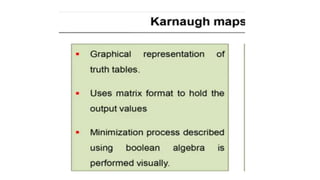
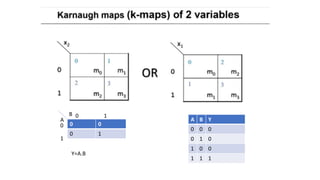
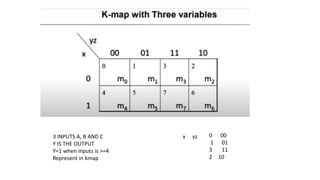
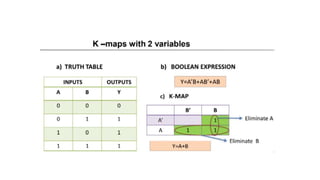
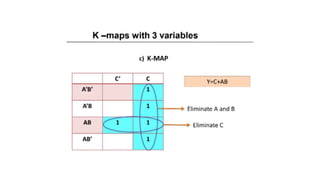
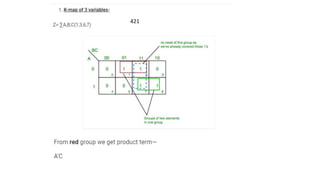
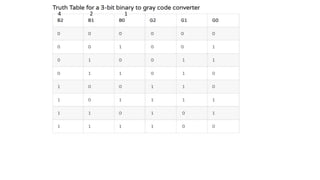
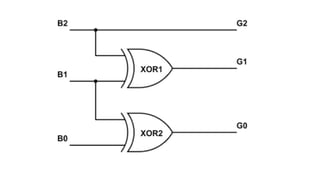
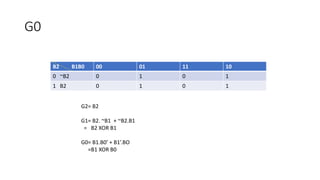
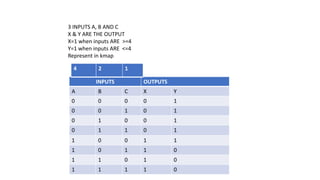
The document provides information about Unit 2 of a course which includes: - Boolean algebra rules and laws such as commutative, associative, distributive for AND, OR and inversion. De Morgan's theorem. - Simplifying logic equations using Boolean algebra rules and Karnaugh maps up to 4 bits. - Converting between binary and gray codes. - Minimizing logic expressions using Karnaugh maps.

1. Unit 2 Boolean algebra and Karnaugh maps
Boolean algebra rules and Boolean laws: Commutative,
Associative, Distributive, AND, OR and Inversion laws, De
Morgan’s theorem, Universal gates, Simplifications of Logic
equations using Boolean algebra rules and Karnaugh map (up
to 4 bit).
Lab Session: - Binary to Gray Interconversion of Logic Gates

2. Boolean Algebra

16. =A.1=A

17. A B ~A ~B ~A.~B (A+B) ~(A+B)
0 0 1 1 1 0 1
0 1 1 0 0 1 0
1 0 0 1 0 1 0
1 1 0 0 0 1 0

18. A B ~A ~B ~A+~B (A.B) ~(A.B)
0 0 1 1 1 0 1
0 1 1 0 1 0 1
1 0 0 1 1 0 1
1 1 0 0 0 1 0

22. y= A.B+C.D = SOP
Y=(A+B).(C+D) = POS

28. 4 2 1

30. 0 0
0 1
A B Y
0 0 0
0 1 0
1 0 0
1 1 1
0
0
1
1
A
B
Y=A.B

31. 3 INPUTS A, B AND C x yz
Y IS THE OUTPUT
Y=1 when inputs is >=4
Represent in kmap
0 00
1 01
3 11
2 10

32. 3 INPUTS A, B AND C
Y IS THE OUTPUT
Y=1 when of the inputs is >=4
Represent in kmap
A B C Y
0 0 0 0
0 0 1 0
0 1 0 0
0 1 1 0
1 0 0 1
1 0 1 1
1 1 0 1
1 1 1 1
4 2 1

33. 3 INPUTS A, B AND C
X & Y ARE THE OUTPUT
X=1 when inputs ARE >=4
Y=1 when inputs ARE <=4
Represent in kmap
INPUTS OUTPUTS
A B C X Y
0 0 0 0 1
0 0 1 0 1
0 1 0 0 1
0 1 1 0 1
1 0 0 1 1
1 0 1 1 0
1 1 0 1 0
1 1 1 1 0
4 2 1

34. FOR Y =A’+C’.B’
C’ C
AB C 0 1
A’B’ 00 1 1
A’B 01 1 1
AB 11 0 0
AB’ 10 1 0

38. Y= C + AB
Octet : 3 variables are
eliminated
Quad: 2 variables are
eliminated
Pair: 2 variables are
eliminated
BC…> 00 01 11 10
A
0 1 1
1 1 1 1

40. Hence for 3-bit code converters,

41. 4 2 1

43. G2
B2 B1B0 00 01 11 10
0 ~B2 0 0 0 0
1 B2 1 1 1 1
G2= B2
G1= B2. ~B1 + ~B2.B1
= B2 XOR B1
G0= B1.~B0 + ~B1.BO
=B1 XOR B0

44. G1
B2 B1B0 00 01 11 10
0 ~B2 0 0 1 1
1 B2 1 1 0 0
G2= B2
G1= B2. B1’ + B2’.B1
= B2 XOR B1
G0= B1.~B0 + ~B1.BO
=B1 XOR B0
B1’B0’ B1’B0 B1B0 B1B0’

45. G0
B2 B1B0 00 01 11 10
0 ~B2 0 1 0 1
1 B2 0 1 0 1
G2= B2
G1= B2. ~B1 + ~B2.B1
= B2 XOR B1
G0= B1.B0’ + B1’.BO
=B1 XOR B0

46. 110
100
Same=0
Different=1

48. 421

49. Same i/p = 0 output
different i/p’s = 1 output
• B2 b1 b0
1 1 0 binary ------ gray
………………………….
1 0 1
• G2 g1 g0

50. Same i/p = 0 output
different i/p’s = 1 output
• g2 g1 g0
1 1 0 gray------ bin
………………………….
1 0 0
• b2 b1 b0

51. Unit 3: Introduction to
Combinational Circuits
Introduction to Combinational Circuits Basic Logic gates
(NOT, OR, AND) & derived gates (NAND, NOR, EXOR)
Symbol and truth table, half adder, full adder, Half
subtractor, Four bit parallel adder. Multiplexer (4:1),
demultiplexer (1:4) and their applications, Code
converters - Decimal to binary, Hexadecimal to binary,
BCD to decimal, Concept of Encoder & decoder. Lab
Session: - To Study 4: 1 Multiplexer and 1 : Demultiplexer
To Study nibble adder and Subtractor circuit

52. Learning Philosophy : Logic gate

61. • A is input and Y is output
• Y= ~A

62. Y= A*B
n= no.of i/p’s
2^n input combinations in truth table

63. Y=a+b

64. • Y
• Y= ~(a.b)
• Y=____
• Y =A*B = ~(A*B)
____
A*B

65. • Y=(a+b) ____
A+B

66. Y=~a*b + a*~b
OUTPUT=0 if input contains even no.of 1’s
OUTPUT=1 if input contains odd no.of 1’s
• 0110 1101

68. • Y= ~a*~b + a*b

69. • 8 4 2 1
• 16 A B C D Y
• 0 0 0 0 0
• 1 0 0 0 1
• 2 0 0 1 0
• 15 1 1 1 1

71. A Y
0 1
1 0
A B Y(NAND)
0 0 1
0 0 1
1 0 1
1 1 0

72. A B Y
0 0 0
0 1 0
1 0 0
1 1 1
AND GATE USING NAND
GATE

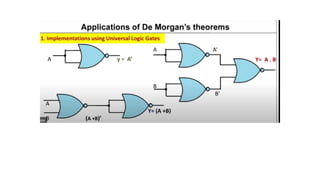
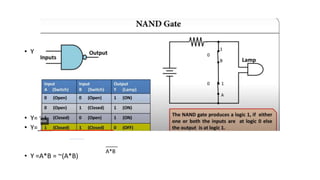
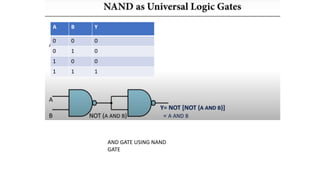
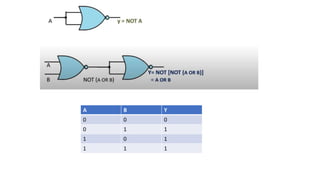
73. • Y= NOT[(NOT A).(NOT B)]
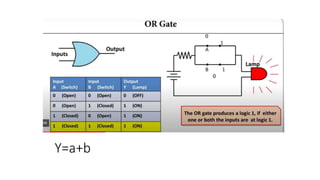
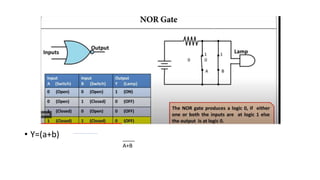
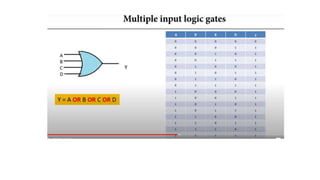
• Y=A+B
OR GATE
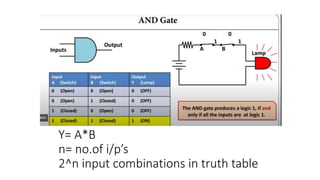
A B Y
0 0 .0
0 1 1
1 0 1
1 1 1
OR GATE USING NAND GATE

74. A B NOR(Y)
0 0 1
0 1 0
1 0 0
1 1 0
A Y
0 1
1 0

75. A B Y
0 0 0
0 1 1
1 0 1
1 1 1

76. A B Y
0 0 0
0 1 0
1 0 0
1 1 1