Mohsin Siddique, profile picture
Uploaded byMohsin Siddique
PDF, PPTX8,480 views

Hydraulic analysis of complex piping systems (updated)

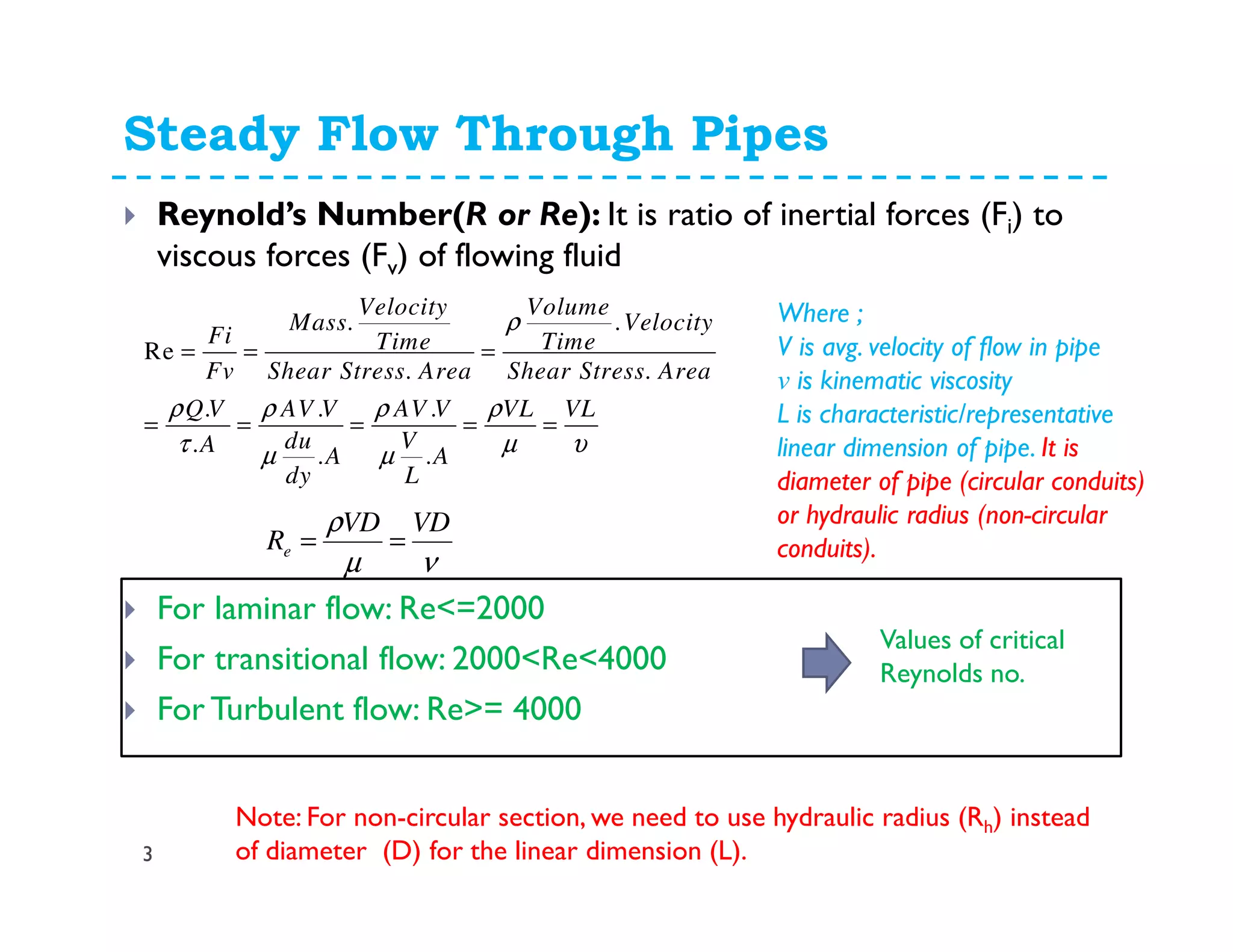
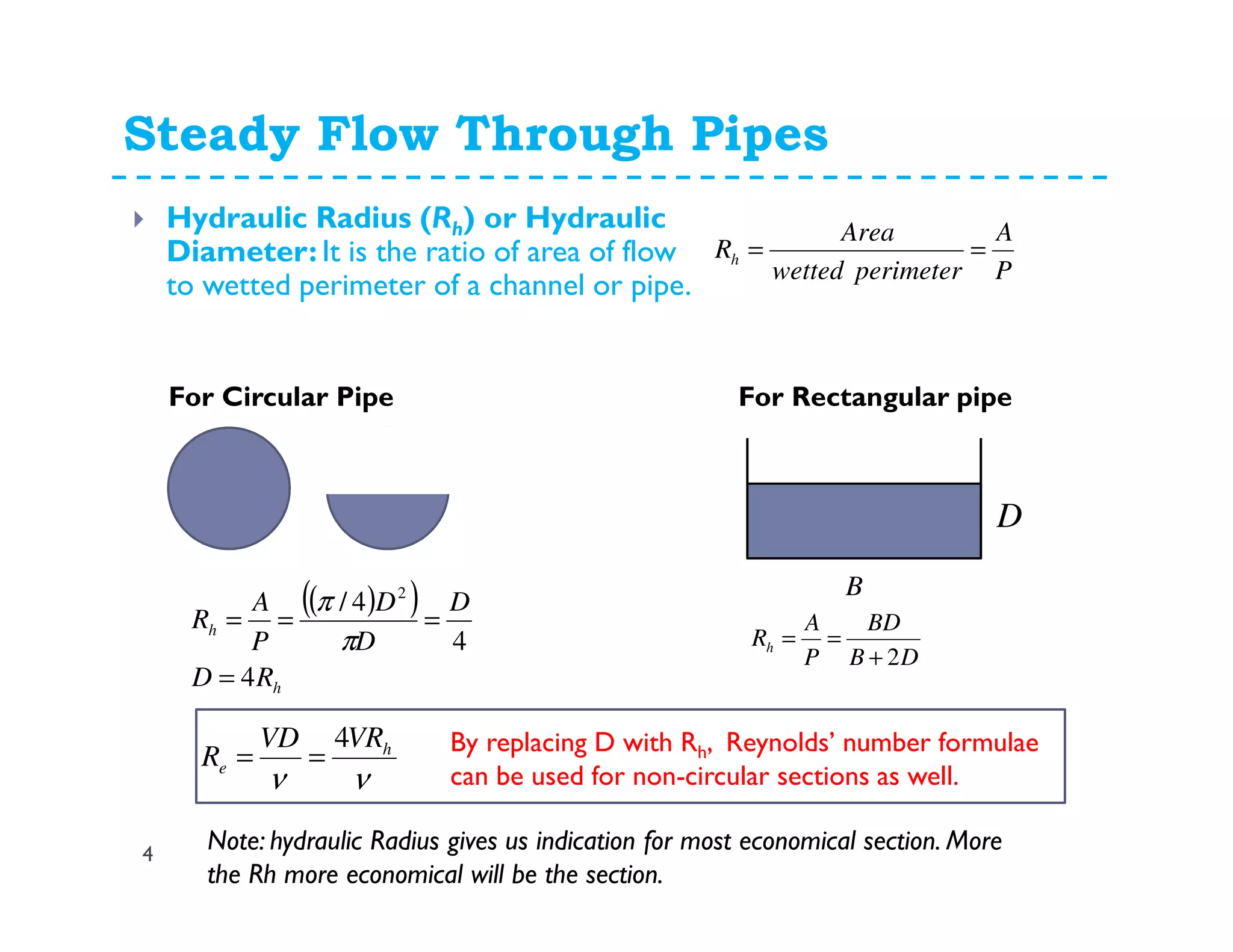
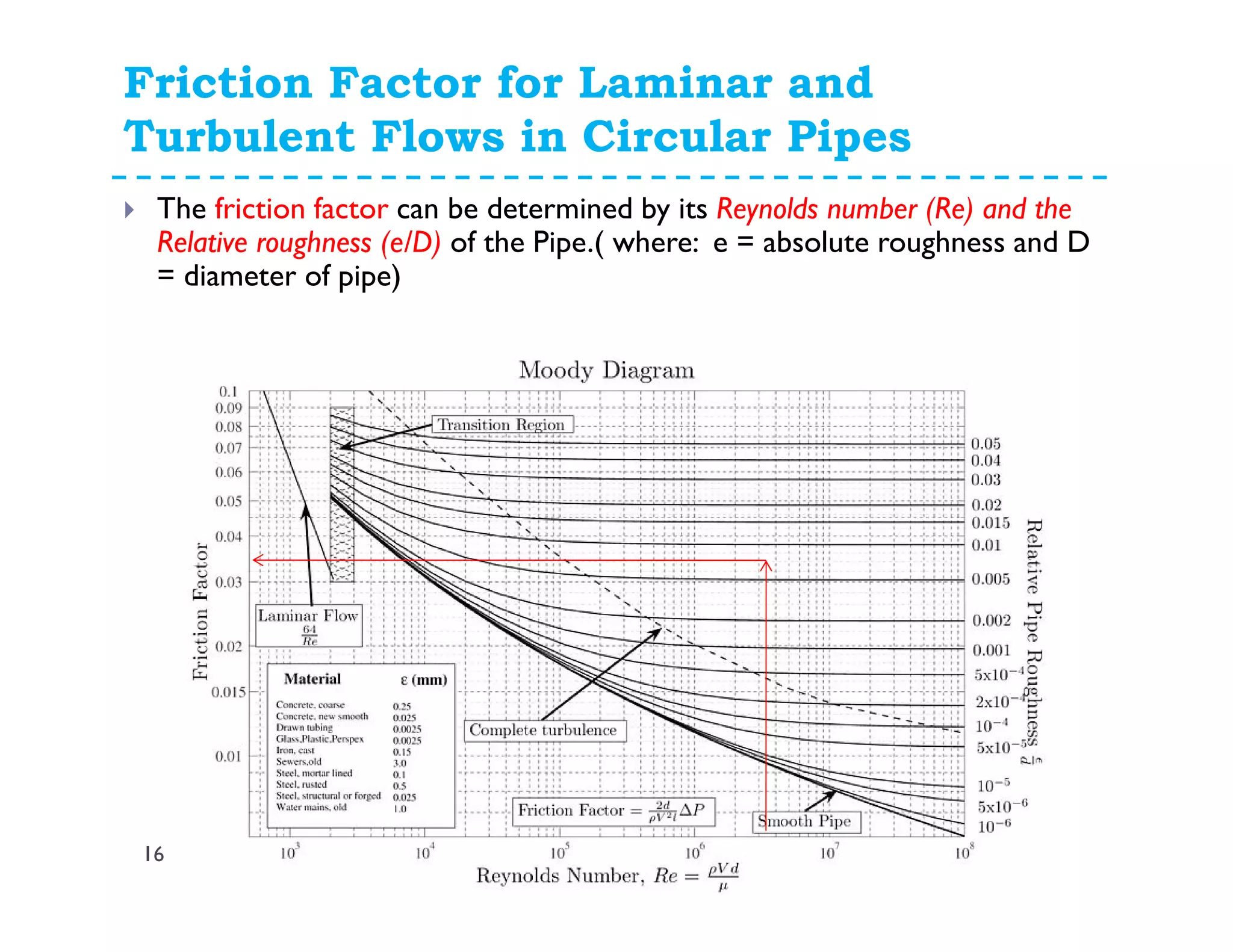
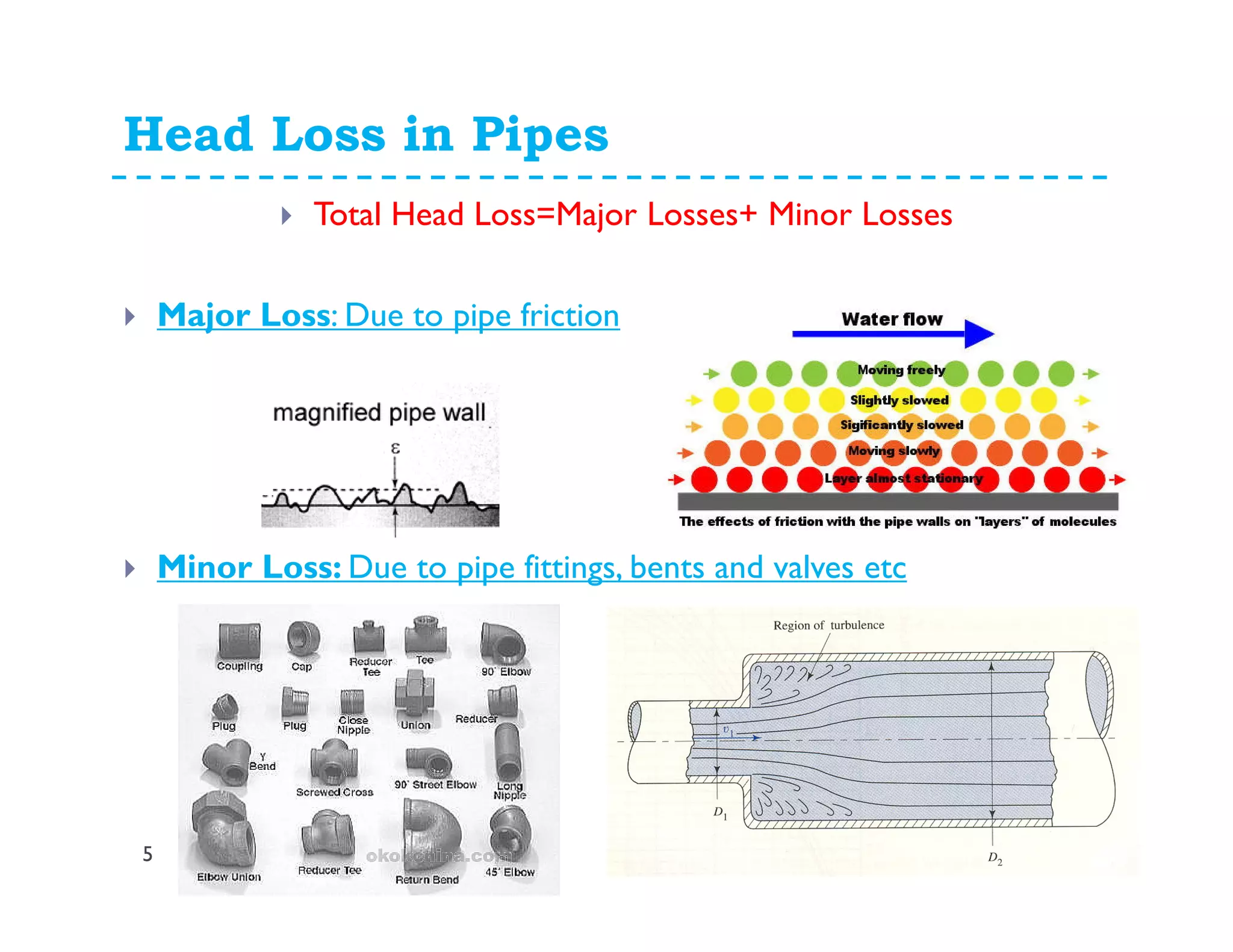
1. Given: Pipe characteristics (D, L, e), fluid properties (ν), flow conditions (Q or V) 2. Calculate Reynold's number (Re) using the given flow parameters 3. Determine friction factor (f) from Moody diagram or equations based on Re and relative roughness (e/D) 4. Use Darcy-Weisbach equation to calculate head loss (hf) or solve for unknown parameter (Q or V)

Embed presentation

Download as PDF, PPTX
Hydraulic analysis of complex piping systems (Losses in pipes, pipes in parallel and pipes in series) 1 Hydraulics Dr. Mohsin Siddique
Steady Flow Through Pipes 2 Laminar Flow: flow in layers Re<2000 (pipe flow) Turbulent Flow: flow layers mixing with each other Re >4000 (pipe flow)
Steady Flow Through Pipes 3 Reynold’s Number(R or Re): It is ratio of inertial forces (Fi) to viscous forces (Fv) of flowing fluid For laminar flow: Re<=2000 For transitional flow: 2000<Re<4000 For Turbulent flow: Re>= 4000 . . Re . . . . . . . . Velocity Volume Mass Velocity Fi Time Time Fv Shear Stress Area Shear Stress Area Q V AV V AV V VL VL du VA A A dy L ρ ρ ρ ρ ρ τ µ υµ µ = = = = = = = = Where ; V is avg. velocity of flow in pipe ν is kinematic viscosity L is characteristic/representative linear dimension of pipe. It is diameter of pipe (circular conduits) or hydraulic radius (non-circular conduits). νµ ρ VDVD Re == Note: For non-circular section, we need to use hydraulic radius (Rh) instead of diameter (D) for the linear dimension (L). Values of critical Reynolds no.
Steady Flow Through Pipes 4 Hydraulic Radius (Rh) or Hydraulic Diameter: It is the ratio of area of flow to wetted perimeter of a channel or pipe. P A perimeterwetted Area Rh == For Circular Pipe ( )( ) h h RD D D D P A R 4 4 4/ 2 = === π π For Rectangular pipe DB BD P A Rh 2+ == B D Note: hydraulic Radius gives us indication for most economical section. More the Rh more economical will be the section. νν h e VRVD R 4 == By replacing D with Rh, Reynolds’ number formulae can be used for non-circular sections as well.
Head Loss in Pipes 5 Total Head Loss=Major Losses+ Minor Losses Major Loss: Due to pipe friction Minor Loss: Due to pipe fittings, bents and valves etc
Head Loss in Pipes due to Friction 6 The head loss due to friction in a given length of pipe is proportional to mean velocity of flow (V) as long as the flow in laminar. i.e., But with increasing velocity, as the flow become turbulent the head loss also varies and become proportion toVn Where n ranges from 1.75 to 2 Log-log plot for flow in uniform pipe (n=2.0 for rough wall pipe; n=1.75 for smooth wall pipe) VH f ∝ n f VH ∝
Frictional Head Loss in Conduits of Constant Cross-Section 7 Consider stead flow in a conduit of uniform cross-section A.The pressure at section 1 & 2 are P1 & P2 respectively.The distance between the sections is L. For equilibrium in stead flow, ∑ == 0maF Figure: Schematic diagram of conduit 0sin 21 =−−− APPLWAP oτα P= perimeter of conduit = Avg. shear stress between pipe boundary and liquid oτ 012 21 =−      − −− PL L zz ALAPAP oτγ αsin12 =      − L zz
Frictional Head Loss in Conduits of Constant cross-section 8 012 21 =−      − −− PL L zz ALAPAP oτγ Dividing the equation by Aγ ( ) 012 21 =−−−− A PL zz PP o γ τ γγ fL o hh A PLP z P z ===      +−      + γ τ γγ 2 2 1 1 Therefore, head loss due to friction, hf, can be written as; h oo f R L A PL h γ τ γ τ == Lh g v z P g v z P +++=++ 22 2 2 2 2 2 1 1 1 γγ Remember !! For pipe flow For stead flow in pipe of uniform diameter v1=v2 Lhz P z P =      +−      + 2 2 1 1 γγ This is general equation and can be applied to any shape conduit having either Laminar or turbulent flow. P A Rh =Q
Determining Shear Stress 9 For smooth-walled pipes/conduits, the average shear stress at the wall is Using Rayleigh's Theorem of dimensional analysis, the above relation can be written as; Rewriting above equation in terms of dimension (FLT), we get ( ),,,, VRf ho ρµτ = ( )                           = ncb a T L L FT L FT LK L F 4 2 22 ( )ncba ho VRk ... ρµτ = LlengthR L F areaforce h o == == 2 /τ ( ) 22 4233 /. //// / − == === = FTLmsN LFTLaFLM TLV µ ρ( ) ( ) ( ) ( )( )ncba TLLFTFTLLKFL /4222 −−− =
Determining Shear Stress 10 According to dimensional homogeneity, the dimension must be equal on either side of the equation, i.e., ( ) ( ) ( ) ( )( )ncba TLLFTFTLLKFL /4222 −−− = )(20: )(422: )(1: iiincbT iincbaL icbF →−+= →+−−=− →+= Solving three equations, we get 1;2;2 −=−=−= ncnbna Substituting values back in above equation ( ) ( ) 2 2 122 ...... V VR kVRkVRk n hnnnn h ncba ho ρ µ ρ ρµρµτ − −−−       === ( ) 22 VRk n eo ρτ − = Setting = we get 2 2 V Cfo ρτ = Where, Cf is the coefficient of friction ( ) 2−n eRk 2/fC (Re)fCf =
Determining Shear Stress 11 Now substituting the equation of avg. shear stress in equation of head loss, For circular pipe flows, Rh=D/4 Where, f is a friction factor. i.e., The above equation is known as pipe friction equation and as Darcy- Weisbach equation and is used for calculation of pipe-friction head loss for circular pipes flowing full (laminar or turbulent) 2/2 VCfo ρτ = h o f R L h γ τ = h f h f f gR LVC R LVC h 22 22 == γ ρ g V D L fh g V D L C Dg LVC h f f f f 2 2 4 42 4 2 22 = == fCf 4=Q
Friction Factor for Laminar and Turbulent Flows in Circular Pipes 12 Smooth and Rough Pipe A smooth pipe is the one which behaves as smooth pipe i.e. (frictionless). It is quite possible that a pipe may behave as smooth at a certain flow condition while at some other condition it may behave rough. Mathematically; Smooth Pipe Rough Pipe Transitional mode Turbulent flow near boundary = = v e δ Roughness height Thickness of viscous sub-layer Smooth pipe Rough pipe f D fV v Re 14.1414.14 == ν δ ve δ< ve δ> ve δ< ve δ14> vv e δδ 14≤≤
Friction Factor for Laminar and Turbulent Flows in Circular Pipes 13 For laminar flow For turbulent flow Re 64 =f2000Re < 51.2 Re log2 1 f f = 9.6 Re log8.1 1 = f 25.0 Re 316.0 =f 7/1 max       = or y u u Def / 7.3 log2 1 =         +−= f De f Re 51.2 7.3 / log2 1         +      −= Re 9.6 7.3 / log8.1 1 11.1 De f Colebrook Eq. for turbulent flow in all pipes Halaand Eq. For turbulent flow in all pipes Von-karman Eq. for fully rough flow Blacius Eq. for smooth pipe flow Seventh-root law 5 10Re3000 ≤≤ From Nikuradse experiments Colebrook Eq. for smooth pipe flow for smooth pipe flow 4000Re >
Friction Factor for Laminar and Turbulent Flows in Circular Pipes 14 The Moody chart or Moody diagram is a graph in non- dimensional form that relates the Darcy-Weisbach friction factor, Reynolds number and relative roughness for fully developed flow in a circular pipe. The Moody chart is universally valid for all steady, fully developed, incompressible pipe flows.
Friction Factor for Laminar and Turbulent Flows in Circular Pipes 15 For laminar flow For non-laminar flow eR f 64 =         +−= f De f Re 51.2 7.3 / log2 1 Colebrook eq.
Friction Factor for Laminar and Turbulent Flows in Circular Pipes 16 The friction factor can be determined by its Reynolds number (Re) and the Relative roughness (e/D) of the Pipe.( where: e = absolute roughness and D = diameter of pipe)
17 Absolute roughness
Problem Types 18 Type 1: Determine f and hf, Type 2: Determine Q Type 3: Determine D
Problem 19 Find friction factor for the following pipe e=0.002 ft D=1ft KinematicViscosity, ν=14.1x10-6ft2/s Velocity of flow,V=0.141ft/s Solution: e/D=0.002/1=0.002 R=VD/ ν =1x0.141/(14.1x10-6)=10000 From Moody’s Diagram; f=0.034 ___________ Re 51.2 7.3 / log2 1 =         +−= f f De f
Problem-Type 1 20 Pipe dia, D= 3 inch & L=100m Re=50,000 ʋ=1.059x10-5ft2/s (a): Laminar flow: f=64/Re=64/50,000=0.00128 ft gD fLV HLf 0357.0 )12/3)(2.32(2 )12.2)(100(00128.0 2 22 === sftV VVD /12.2 10059.1 )12/3( 50000Re 5 =⇒ × =⇒= − ν
Problem-Type 1 21 Pipe dia, D= 3 inch & L=100m Re=50,000 ʋ=1.059x10-5ft2/s (b): Turbulent flow in smooth pipe: i.e.: e=0 0209.0 50000 51.2 7.3 0 log2 Re 51.2 7.3 / log2 1 =         +−=         +−= f ff De f ft gD fLV HLf 582.0 )12/3)(2.32(2 )12.2)(100(0209.0 2 22 ===
Problem-Type 1 22 Pipe dia, D= 3 inch & L=100m Re=50,000 ʋ=1.059x10-5ft2/s (c): Turbulent flow in rough pipe: i.e.: e/D=0.05 0720.0 50000 51.2 7.3 05.0 log2 Re 51.2 7.3 / log2 1 =         +−=         +−= f ff De f ft gD fLV HLf 01.2 )12/3)(2.32(2 )12.2)(100(0720.0 2 22 ===
Problem-Type 1 23 hL=? memDmL 0005.0;25.0;1000 === smsmQ /10306.1;/051.0 263 − ×== ν ( ) ( ) 002.025.0/0005.0/ 10210306.1/25.0039.1/ 56 == ×=××== − De VDR ν 0.0245f DiagramsMoody'From = m gD fLV hL 39.5 2 2 == smAQV /039.1/ ==Q
Problem-Type 2 24 gDfLVhL 2/2 =
Problem-Type 2 25 For laminar flow For non-laminar flow eR f 64 =         +−= f De f Re 51.2 7.3 / log2 1 Colebrook eq.
Problem-Type 3 26
Problem 27 gD flV h f De f Lf 2 Re 51.2 7.3 / log2 1 2 =         +−=
Problem 28
Problem 29
MINOR LOSSES 30 Each type of loss can be quantified using a loss coefficient (K). Losses are proportional to velocity of flow and geometry of device. Where, Hm is minor loss and K is minor loss coefficient.The value of K is typically provided for various types/devices NOTE: If L > 1000D minor losses become significantly less than that of major losses and hence can be neglected. g V KHm 2 2 =
Categories of Minor Losses 31 These can be categorized as 1. Head loss due to contraction in pipe 1.1 Sudden Contraction 1.2 Gradual Contraction 2. Entrance loss 3. Head loss due to enlargement of pipe 3.1 Sudden Enlargement 3.2 Gradual Enlargement 4. Exit loss 5. Head loss due to pipe fittings 6. Head loss due to bends and elbows
Minor Losses 32 Head loss due to contraction of pipe (Sudden contraction) A sudden contraction (Figure) in pipe usually causes a marked drop in pressure in the pipe because of both the increase in velocity and the loss of energy of turbulence. g V KH cm 2 2 2 = Head loss due to sudden contraction is Where, kc is sudden contraction coefficient and it value depends up ratio of D2/D1 and velocity (V2) in smaller pipe
Minor Losses 33 Head loss due to contraction of pipe (Gradual Contraction) Head loss from pipe contraction may be greatly reduced by introducing a gradual pipe transition known as a confusor as shown Figure. g V KH cm 2 ' 2 2 = Head loss due to gradual contraction is Where, kc ’ is gradual contraction coefficient and it value depends up ratio of D2/D1 and velocity (V2) in smaller pipe
Minor Losses 34 Entrance loss The general equation for an entrance head loss is also expressed in terms of velocity head of the pipe: The approximate values for the entrance loss coefficient (Ke) for different entrance conditions are given below g V KH em 2 2 =
Minor Losses 35 head loss due to enlargement of pipe (Sudden Enlargement) The behavior of the energy grade line and the hydraulic grade line in the vicinity of a sudden pipe expansion is shown in Figure The magnitude of the head loss may be expressed as ( ) g VV Hm 2 2 21 − =
Minor Losses 36 head loss due to enlargement of pipe (Gradual Enlargement) The head loss resulting from pipe expansions may be greatly reduced by introducing a gradual pipe transition known as a diffusor The magnitude of the head loss may be expressed as ( ) g VV KH em 2 2 21 − = The values of Ke’ vary with the diffuser angle (α).
Minor Losses 37 Exit Loss A submerged pipe discharging into a large reservoir (Figure ) is a special case of head loss from expansion. ( ) g V KH dm 2 2 = Exit (discharge) head loss is expressed as where the exit (discharge) loss coefficient Kd=1.0.
Minor Losses 38 Head loss due to fittings valves Fittings are installed in pipelines to control flow.As with other losses in pipes, the head loss through fittings may also be expressed in terms of velocity head in the pipe: g V KH fm 2 2 =
Minor Losses 39 Head loss due to bends The head loss produced at a bend was found to be dependent of the ratio the radius of curvature of the bend (R) to the diameter of the pipe (D).The loss of head due to a bend may be expressed in terms of the velocity head as For smooth pipe bend of 900, the values of Kb for various values of R/D are listed in following table. g V KH bm 2 2 =
Minor Losses 40
Numerical Problems 41
Numerical Problems 42
Pipes in Series 43 If a pipeline is made up of lengths of different diameters, as shown in figure, conditions must satisfy the continuity and energy equations; If Q is given, the problem is straight forward. Total head loss can be estimated by adding the contributions from various sections as; νπ VD R gD LV fh D Q V L === , 2 , 4 2 2 Friction coefficient f, can be constant values given in problem or variable estimated from material and flow properties. i.e. e/D,V, R and f If head loss is given and discharge is required then either of the two methods namely equivalent velocity head method or equivalent length method many be used.;
Pipes in Series 44 (1). Equivalent-velocity-head method: In this method a more accurate approach of DarcyWeisbach is applied to estimate Q. ...321 +++= LLLL hhhh Above equation considering minor losses becomes as; ... 222 2 3 3 3 3 2 2 2 2 2 2 1 1 1 1 +      ++      ++      += ∑∑∑ g V K D L f g V K D L f g V K D L fhL Now using continuity equation, we can write 3 2 31 2 12 2 21 2 1 3 2 32 2 21 2 13 2 32 2 21 2 1221 , 444 VDVDVDVD VDVDVDVDVDVDQQQ == ==⇒==⇒== πππ From above, all velocities can be expressed in terms of chosen velocity (V). (1). Equivalent velocity head method (2). Equivalent length method If Q is not given:
Pipes in Series 45 (2). Equivalent length method: In this method, all pipes are expressed in terms of equivalent lengths to one given pipe size By equivalent length is meant a length, Le, of pipe of a certain diameter, De, and friction factor, fe, which for the same flow will give same head loss as the pipe under consideration of length, L, diameter, D, and friction factor, f 5 2 2 2/ 2/       == D De fe f L gVe gV D De fe f LLe
Pipes in Series 46 Problem: Suppose in the Figure the pipes 1, 2, 3 are 300m of 30cm diameter, 150m of 20cm diameter and 250m of 25cm diameter, respectively, of new cast iron and are conveying 15oC water. If h=10m, find the rate of flow from A to B. Figure
47 From moody diagram, we
Pipes in Series 48 5 2 2 2/ 2/       == D De fe f L gVe gV D De fe f LLe
Pipes in Parallel 49 In the case of flow through two or more parallel pipes, as shown in fig, the continuity and energy equations establish the following relations which must be satisfied. According to Darcy-Weisbach equation, the head loss including minor losses can be written as; g V K D L fhL 2 2       += ∑       + = ∑K D L f gh V L2
Pipes in Parallel 50 According to continuity equation L L hC K D L f gh AAVQ =       + == ∑ 2 Where, C is constant for given pipe. Now according to governing equation for pipe flow, we can write as; ( ) L LLL hCCCQ hChChCQ QQQQ ... .. ... 321 221 321 +++= +++= +++= Above equations enable us to find a first estimate of hL and the distribution of flows and velocities in pipes. Using these, we can next make improvements to the values of f and if necessary repeat them until we finally make a correct determination of hL and distribution of flows.
Pipes in Parallel 51 Find the flow rates in each pipe ?
Pipes in Parallel 52 Energy eq. Head loss Eq. for parallel pipes
Pipes in Parallel 53
Problem 54 Suppose in the Figure the pipes 1, 2, 3 are 150m of 80mm diameter, 60m of 50mm diameter and 120m of 60mm diameter, respectively, of new wrough iron pipe (e=0.000046m). If hL=6m, find the rate of flow from A to B. Take kinematic viscosity as 4.26x10-5m2/s Answer: 1.5L/s
Problem 55
Problem 56 In fig. pipe 1 is 500ft of 2-in, pipe 2 is 350ft of 3-in, and pipe 3 is 750ft of 4- in diameter, all of smooth brass (e=0.0005ft). Crude oil (s=0.855 and kinematic viscosity of 7.6x10-5ft2/s) is flow at 0.7 cfs. Find the head loss from A to B and the flow in each pipe. Answer:
Problem 57
58
Thank you Questions…. 59

More Related Content

PPT
Flow through pipes ppt
byVishal Chaudhari
 
PDF
Flow Through Pipe
bysumitt6_25730773
 
PDF
0 open channel intro 5
byRefee Lubong
 
PPT
open channel flow
byGeoRuizO
 
PPTX
Open Channel Flow
byMalla Reddy University
 
PPTX
Open channel flow
bykamariya keyur
 
PPSX
Geotechnical Engineering-I [Lec #27: Flow Nets]
byMuhammad Irfan
 
PPTX
Water hammer
byNaveen Sudharsan
 
Flow through pipes ppt
byVishal Chaudhari
 
Flow Through Pipe
bysumitt6_25730773
 
0 open channel intro 5
byRefee Lubong
 
open channel flow
byGeoRuizO
 
Open Channel Flow
byMalla Reddy University
 
Open channel flow
bykamariya keyur
 
Geotechnical Engineering-I [Lec #27: Flow Nets]
byMuhammad Irfan
 
Water hammer
byNaveen Sudharsan
 

What's hot

PDF
Pipe network analysis with examples
byMohsin Siddique
 
PDF
Chapter 2 open channel hydraulics
byMohsin Siddique
 
PPTX
Class lectures on hydrology by Rabindra Ranjan Saha, Lecture 8
byWorld University of Bangladesh
 
PDF
Flow measurement
byMohsin Siddique
 
PDF
Control Seepage Thought Earth Dams
byAhmed Mansor
 
PDF
Void Ratio Correlations
byAli Rehman
 
PPTX
Specific Energy Curves
byGaurav Verma
 
PPTX
Flow through pipes
byChirag Bhanagale
 
PPT
Types of flow in open channel
byMir Zafarullah
 
PDF
Introduction to Hydrology, Stream Gauging
byAmol Inamdar
 
PPT
Design Of Hydraulic Structure - Kennedy's Theory
byLatif Hyder Wadho
 
PPTX
Notches and weir
byDewang Agrawal
 
PDF
Open channel design
byMohsin Siddique
 
PPTX
Flow through orifice meter
byPulkit Shukla
 
PDF
Permeability of Soil
byArbaz Kazi
 
PPTX
Turbine and pump.pptx
byMdToukirShah
 
PPTX
Chapter 8:Hydraulic Jump and its characterstics
byBinu Khadka
 
PPTX
Hydraulic jump
byVenkata Sai Kari
 
PPTX
VENTURIMETER -Application of Bernoulli's Law
byKundan Kumar
 
PPTX
Quick sand condation
byEngr Khalil Dawar ( Gold Medalist )
 
Pipe network analysis with examples
byMohsin Siddique
 
Chapter 2 open channel hydraulics
byMohsin Siddique
 
Class lectures on hydrology by Rabindra Ranjan Saha, Lecture 8
byWorld University of Bangladesh
 
Flow measurement
byMohsin Siddique
 
Control Seepage Thought Earth Dams
byAhmed Mansor
 
Void Ratio Correlations
byAli Rehman
 
Specific Energy Curves
byGaurav Verma
 
Flow through pipes
byChirag Bhanagale
 
Types of flow in open channel
byMir Zafarullah
 
Introduction to Hydrology, Stream Gauging
byAmol Inamdar
 
Design Of Hydraulic Structure - Kennedy's Theory
byLatif Hyder Wadho
 
Notches and weir
byDewang Agrawal
 
Open channel design
byMohsin Siddique
 
Flow through orifice meter
byPulkit Shukla
 
Permeability of Soil
byArbaz Kazi
 
Turbine and pump.pptx
byMdToukirShah
 
Chapter 8:Hydraulic Jump and its characterstics
byBinu Khadka
 
Hydraulic jump
byVenkata Sai Kari
 
VENTURIMETER -Application of Bernoulli's Law
byKundan Kumar
 
Quick sand condation
byEngr Khalil Dawar ( Gold Medalist )
 

Similar to Hydraulic analysis of complex piping systems (updated)

PDF
Fluid MechanicsLosses in pipes dynamics of viscous flows
byMohsin Siddique
 
PDF
Hydraulic losses in pipe
byMOHAMMAD ATIF ALI
 
PDF
010a (PPT) Flow through pipes.pdf .
byhappycocoman
 
PPT
Flow through pipes
bysumitt6_25730773
 
PPT
Closed conduct flow
byDr. Ezzat Elsayed Gomaa
 
PDF
Laminar turbulent
bykrajesh11111
 
PPT
Flow In Pipes
byIla Lee
 
PPTX
Flow of incompressible fluids through pipes
byMAULIKM1
 
PDF
008
byphysics101
 
PDF
final friction in pipes
byAbhishek Dabas
 
PPT
Pipe sizing
byAjay Kumar Sharma
 
PPT
update__lecture_3.ppt
bybharatsingh300
 
PPTX
Fluid Mech. Presentation 2nd year B.Tech.
byshivam gautam
 
PDF
Lecture 6
byEyoase Nathan
 
DOCX
Thesis Report
bySamiha Nazrul
 
PPT
Closed conduct flow
byDr. Ezzat Elsayed Gomaa
 
PPTX
Module 4 - flow through a pipe - Fluid Dynamics
byVigilJVijayan
 
PDF
1 resistance
byRefee Lubong
 
PPTX
Lwce 301 fluid mechanics
byPMAS-AAUR
 
PPTX
Hydraulics and open channel flow-Fluid Mechanics
byEngrKaisanMuhammadUs
 
Fluid MechanicsLosses in pipes dynamics of viscous flows
byMohsin Siddique
 
Hydraulic losses in pipe
byMOHAMMAD ATIF ALI
 
010a (PPT) Flow through pipes.pdf .
byhappycocoman
 
Flow through pipes
bysumitt6_25730773
 
Closed conduct flow
byDr. Ezzat Elsayed Gomaa
 
Laminar turbulent
bykrajesh11111
 
Flow In Pipes
byIla Lee
 
Flow of incompressible fluids through pipes
byMAULIKM1
 
008
byphysics101
 
final friction in pipes
byAbhishek Dabas
 
Pipe sizing
byAjay Kumar Sharma
 
update__lecture_3.ppt
bybharatsingh300
 
Fluid Mech. Presentation 2nd year B.Tech.
byshivam gautam
 
Lecture 6
byEyoase Nathan
 
Thesis Report
bySamiha Nazrul
 
Closed conduct flow
byDr. Ezzat Elsayed Gomaa
 
Module 4 - flow through a pipe - Fluid Dynamics
byVigilJVijayan
 
1 resistance
byRefee Lubong
 
Lwce 301 fluid mechanics
byPMAS-AAUR
 
Hydraulics and open channel flow-Fluid Mechanics
byEngrKaisanMuhammadUs
 

More from Mohsin Siddique

PDF
Dymanics of open channel flow
byMohsin Siddique
 
PDF
Chapter 4 seepage theories
byMohsin Siddique
 
PDF
Fluid kinematics
byMohsin Siddique
 
PDF
Chapter 7 spillway and energy dissipators
byMohsin Siddique
 
PDF
Chapter 3 linear wave theory and wave propagation
byMohsin Siddique
 
PDF
Chapter 5 drop sturcutures
byMohsin Siddique
 
PDF
Fluid MechanicsVortex flow and impulse momentum
byMohsin Siddique
 
PDF
Fluid dynamic
byMohsin Siddique
 
PDF
Buoyancy and floatation
byMohsin Siddique
 
PDF
Chapter 3 channel design
byMohsin Siddique
 
PDF
Chapter 6 concrete dam engineering with examples
byMohsin Siddique
 
PDF
Chapter 1 introduction to hydraulics structures history...
byMohsin Siddique
 
PDF
Chapter 2 wave and tides with examples
byMohsin Siddique
 
PDF
Chapter 4 Introduction to beach processes and management strategies
byMohsin Siddique
 
PDF
Engineering Economics: Solved exam problems [ch1-ch4]
byMohsin Siddique
 
PDF
Chapter 1 introduction to coastal engineering and management strategies
byMohsin Siddique
 
PDF
Chapter 5 coastal structures
byMohsin Siddique
 
PDF
Basics of image processing using MATLAB
byMohsin Siddique
 
PDF
Particle image velocimetry
byMohsin Siddique
 
PDF
Basics of image processing & analysis
byMohsin Siddique
 
Dymanics of open channel flow
byMohsin Siddique
 
Chapter 4 seepage theories
byMohsin Siddique
 
Fluid kinematics
byMohsin Siddique
 
Chapter 7 spillway and energy dissipators
byMohsin Siddique
 
Chapter 3 linear wave theory and wave propagation
byMohsin Siddique
 
Chapter 5 drop sturcutures
byMohsin Siddique
 
Fluid MechanicsVortex flow and impulse momentum
byMohsin Siddique
 
Fluid dynamic
byMohsin Siddique
 
Buoyancy and floatation
byMohsin Siddique
 
Chapter 3 channel design
byMohsin Siddique
 
Chapter 6 concrete dam engineering with examples
byMohsin Siddique
 
Chapter 1 introduction to hydraulics structures history...
byMohsin Siddique
 
Chapter 2 wave and tides with examples
byMohsin Siddique
 
Chapter 4 Introduction to beach processes and management strategies
byMohsin Siddique
 
Engineering Economics: Solved exam problems [ch1-ch4]
byMohsin Siddique
 
Chapter 1 introduction to coastal engineering and management strategies
byMohsin Siddique
 
Chapter 5 coastal structures
byMohsin Siddique
 
Basics of image processing using MATLAB
byMohsin Siddique
 
Particle image velocimetry
byMohsin Siddique
 
Basics of image processing & analysis
byMohsin Siddique
 

Recently uploaded

PDF
0acebd80-08f7-4be1-9135-15abe45dbc94.pdf
bySirvan7
 
PPTX
Basics of internal combustio nengines, vapor compression cycle
byPrashantPatunkar1
 
PPTX
Forouzan6e_ch02_PPTs_Physical.pptxmcgrawhill
byshaiviadesh
 
PPTX
pH-Responsive Polymers: Synthesis, Properties, and Biomedical Applications
byBURAKALPERENKARABULU
 
PDF
Dimensional Analysis and modelling similitude
by360degrees1
 
PPTX
PVD MNA 501 Recipe Review with understanding
byNritaGaur1
 
PPTX
MET 464 /MOD 2/MIRCO AND NANO MANUFACTURING/SESSION 1.pptx
byVINAY B
 
PDF
22nd Safety Convention by IE(I) dt 27.12.25 by Rajesh Prasad.pdf
byRajesh Prasad
 
PPTX
STM Unit 2 Complete notes for engineering students for better understanding
byLakshmiVivekaKesanap
 
PPT
Data Streams and Mining_1.ppt UNIT ONE COVERED
byBhupendraSingh564079
 
PPTX
Introduction to Physical Metallurgy II.pptx
byOcheriCyril2
 
PPTX
Module 1 AGGREGATES, DEFINITION, TYPES .pptx
bytkmmullonkal
 
PPTX
chapterOverview - embedded systems .pptx
bysamyukthakg2020
 
PPTX
Unit 2 - ABRASIVE PROCESS AND BROACHING.pptx
byarivazhaganrajangam
 
PPTX
SOFTWARE PROJECT MANAGEMENT PART 2-2.pptx
byssuserbafe2d
 
PDF
Module 3 Python progr1BPLCK105B-By Dr.SV.pdf
bySURESHA V
 
PPT
DECISION MAKING SYSTEMS Modelling and Support
byAnu S S
 
PPTX
reference material iso 45001_2018.pptx reference material iso 45001_2018.pptx
byMelwinPaul6
 
PPT
Introduction to ARTIFICIAL INTELLIGENCES
byKAVITHAA49
 
PPTX
researchproposalpresentation-141127024318-conversion-gate02.pptx
bybcabcu20222025
 
0acebd80-08f7-4be1-9135-15abe45dbc94.pdf
bySirvan7
 
Basics of internal combustio nengines, vapor compression cycle
byPrashantPatunkar1
 
Forouzan6e_ch02_PPTs_Physical.pptxmcgrawhill
byshaiviadesh
 
pH-Responsive Polymers: Synthesis, Properties, and Biomedical Applications
byBURAKALPERENKARABULU
 
Dimensional Analysis and modelling similitude
by360degrees1
 
PVD MNA 501 Recipe Review with understanding
byNritaGaur1
 
MET 464 /MOD 2/MIRCO AND NANO MANUFACTURING/SESSION 1.pptx
byVINAY B
 
22nd Safety Convention by IE(I) dt 27.12.25 by Rajesh Prasad.pdf
byRajesh Prasad
 
STM Unit 2 Complete notes for engineering students for better understanding
byLakshmiVivekaKesanap
 
Data Streams and Mining_1.ppt UNIT ONE COVERED
byBhupendraSingh564079
 
Introduction to Physical Metallurgy II.pptx
byOcheriCyril2
 
Module 1 AGGREGATES, DEFINITION, TYPES .pptx
bytkmmullonkal
 
chapterOverview - embedded systems .pptx
bysamyukthakg2020
 
Unit 2 - ABRASIVE PROCESS AND BROACHING.pptx
byarivazhaganrajangam
 
SOFTWARE PROJECT MANAGEMENT PART 2-2.pptx
byssuserbafe2d
 
Module 3 Python progr1BPLCK105B-By Dr.SV.pdf
bySURESHA V
 
DECISION MAKING SYSTEMS Modelling and Support
byAnu S S
 
reference material iso 45001_2018.pptx reference material iso 45001_2018.pptx
byMelwinPaul6
 
Introduction to ARTIFICIAL INTELLIGENCES
byKAVITHAA49
 
researchproposalpresentation-141127024318-conversion-gate02.pptx
bybcabcu20222025
 

Hydraulic analysis of complex piping systems (updated)

  • 1.
    Hydraulic analysis ofcomplex piping systems (Losses in pipes, pipes in parallel and pipes in series) 1 Hydraulics Dr. Mohsin Siddique
  • 2.
    Steady Flow ThroughPipes 2 Laminar Flow: flow in layers Re<2000 (pipe flow) Turbulent Flow: flow layers mixing with each other Re >4000 (pipe flow)
  • 3.
    Steady Flow ThroughPipes 3 Reynold’s Number(R or Re): It is ratio of inertial forces (Fi) to viscous forces (Fv) of flowing fluid For laminar flow: Re<=2000 For transitional flow: 2000<Re<4000 For Turbulent flow: Re>= 4000 . . Re . . . . . . . . Velocity Volume Mass Velocity Fi Time Time Fv Shear Stress Area Shear Stress Area Q V AV V AV V VL VL du VA A A dy L ρ ρ ρ ρ ρ τ µ υµ µ = = = = = = = = Where ; V is avg. velocity of flow in pipe ν is kinematic viscosity L is characteristic/representative linear dimension of pipe. It is diameter of pipe (circular conduits) or hydraulic radius (non-circular conduits). νµ ρ VDVD Re == Note: For non-circular section, we need to use hydraulic radius (Rh) instead of diameter (D) for the linear dimension (L). Values of critical Reynolds no.
  • 4.
    Steady Flow ThroughPipes 4 Hydraulic Radius (Rh) or Hydraulic Diameter: It is the ratio of area of flow to wetted perimeter of a channel or pipe. P A perimeterwetted Area Rh == For Circular Pipe ( )( ) h h RD D D D P A R 4 4 4/ 2 = === π π For Rectangular pipe DB BD P A Rh 2+ == B D Note: hydraulic Radius gives us indication for most economical section. More the Rh more economical will be the section. νν h e VRVD R 4 == By replacing D with Rh, Reynolds’ number formulae can be used for non-circular sections as well.
  • 5.
    Head Loss inPipes 5 Total Head Loss=Major Losses+ Minor Losses Major Loss: Due to pipe friction Minor Loss: Due to pipe fittings, bents and valves etc
  • 6.
    Head Loss inPipes due to Friction 6 The head loss due to friction in a given length of pipe is proportional to mean velocity of flow (V) as long as the flow in laminar. i.e., But with increasing velocity, as the flow become turbulent the head loss also varies and become proportion toVn Where n ranges from 1.75 to 2 Log-log plot for flow in uniform pipe (n=2.0 for rough wall pipe; n=1.75 for smooth wall pipe) VH f ∝ n f VH ∝
  • 7.
    Frictional Head Lossin Conduits of Constant Cross-Section 7 Consider stead flow in a conduit of uniform cross-section A.The pressure at section 1 & 2 are P1 & P2 respectively.The distance between the sections is L. For equilibrium in stead flow, ∑ == 0maF Figure: Schematic diagram of conduit 0sin 21 =−−− APPLWAP oτα P= perimeter of conduit = Avg. shear stress between pipe boundary and liquid oτ 012 21 =−      − −− PL L zz ALAPAP oτγ αsin12 =      − L zz
  • 8.
    Frictional Head Lossin Conduits of Constant cross-section 8 012 21 =−      − −− PL L zz ALAPAP oτγ Dividing the equation by Aγ ( ) 012 21 =−−−− A PL zz PP o γ τ γγ fL o hh A PLP z P z ===      +−      + γ τ γγ 2 2 1 1 Therefore, head loss due to friction, hf, can be written as; h oo f R L A PL h γ τ γ τ == Lh g v z P g v z P +++=++ 22 2 2 2 2 2 1 1 1 γγ Remember !! For pipe flow For stead flow in pipe of uniform diameter v1=v2 Lhz P z P =      +−      + 2 2 1 1 γγ This is general equation and can be applied to any shape conduit having either Laminar or turbulent flow. P A Rh =Q
  • 9.
    Determining Shear Stress 9 Forsmooth-walled pipes/conduits, the average shear stress at the wall is Using Rayleigh's Theorem of dimensional analysis, the above relation can be written as; Rewriting above equation in terms of dimension (FLT), we get ( ),,,, VRf ho ρµτ = ( )                           = ncb a T L L FT L FT LK L F 4 2 22 ( )ncba ho VRk ... ρµτ = LlengthR L F areaforce h o == == 2 /τ ( ) 22 4233 /. //// / − == === = FTLmsN LFTLaFLM TLV µ ρ( ) ( ) ( ) ( )( )ncba TLLFTFTLLKFL /4222 −−− =
  • 10.
    Determining Shear Stress 10 Accordingto dimensional homogeneity, the dimension must be equal on either side of the equation, i.e., ( ) ( ) ( ) ( )( )ncba TLLFTFTLLKFL /4222 −−− = )(20: )(422: )(1: iiincbT iincbaL icbF →−+= →+−−=− →+= Solving three equations, we get 1;2;2 −=−=−= ncnbna Substituting values back in above equation ( ) ( ) 2 2 122 ...... V VR kVRkVRk n hnnnn h ncba ho ρ µ ρ ρµρµτ − −−−       === ( ) 22 VRk n eo ρτ − = Setting = we get 2 2 V Cfo ρτ = Where, Cf is the coefficient of friction ( ) 2−n eRk 2/fC (Re)fCf =
  • 11.
    Determining Shear Stress 11 Nowsubstituting the equation of avg. shear stress in equation of head loss, For circular pipe flows, Rh=D/4 Where, f is a friction factor. i.e., The above equation is known as pipe friction equation and as Darcy- Weisbach equation and is used for calculation of pipe-friction head loss for circular pipes flowing full (laminar or turbulent) 2/2 VCfo ρτ = h o f R L h γ τ = h f h f f gR LVC R LVC h 22 22 == γ ρ g V D L fh g V D L C Dg LVC h f f f f 2 2 4 42 4 2 22 = == fCf 4=Q
  • 12.
    Friction Factor forLaminar and Turbulent Flows in Circular Pipes 12 Smooth and Rough Pipe A smooth pipe is the one which behaves as smooth pipe i.e. (frictionless). It is quite possible that a pipe may behave as smooth at a certain flow condition while at some other condition it may behave rough. Mathematically; Smooth Pipe Rough Pipe Transitional mode Turbulent flow near boundary = = v e δ Roughness height Thickness of viscous sub-layer Smooth pipe Rough pipe f D fV v Re 14.1414.14 == ν δ ve δ< ve δ> ve δ< ve δ14> vv e δδ 14≤≤
  • 13.
    Friction Factor forLaminar and Turbulent Flows in Circular Pipes 13 For laminar flow For turbulent flow Re 64 =f2000Re < 51.2 Re log2 1 f f = 9.6 Re log8.1 1 = f 25.0 Re 316.0 =f 7/1 max       = or y u u Def / 7.3 log2 1 =         +−= f De f Re 51.2 7.3 / log2 1         +      −= Re 9.6 7.3 / log8.1 1 11.1 De f Colebrook Eq. for turbulent flow in all pipes Halaand Eq. For turbulent flow in all pipes Von-karman Eq. for fully rough flow Blacius Eq. for smooth pipe flow Seventh-root law 5 10Re3000 ≤≤ From Nikuradse experiments Colebrook Eq. for smooth pipe flow for smooth pipe flow 4000Re >
  • 14.
    Friction Factor forLaminar and Turbulent Flows in Circular Pipes 14 The Moody chart or Moody diagram is a graph in non- dimensional form that relates the Darcy-Weisbach friction factor, Reynolds number and relative roughness for fully developed flow in a circular pipe. The Moody chart is universally valid for all steady, fully developed, incompressible pipe flows.
  • 15.
    Friction Factor forLaminar and Turbulent Flows in Circular Pipes 15 For laminar flow For non-laminar flow eR f 64 =         +−= f De f Re 51.2 7.3 / log2 1 Colebrook eq.
  • 16.
    Friction Factor forLaminar and Turbulent Flows in Circular Pipes 16 The friction factor can be determined by its Reynolds number (Re) and the Relative roughness (e/D) of the Pipe.( where: e = absolute roughness and D = diameter of pipe)
  • 17.
  • 18.
    Problem Types 18 Type 1:Determine f and hf, Type 2: Determine Q Type 3: Determine D
  • 19.
    Problem 19 Find friction factorfor the following pipe e=0.002 ft D=1ft KinematicViscosity, ν=14.1x10-6ft2/s Velocity of flow,V=0.141ft/s Solution: e/D=0.002/1=0.002 R=VD/ ν =1x0.141/(14.1x10-6)=10000 From Moody’s Diagram; f=0.034 ___________ Re 51.2 7.3 / log2 1 =         +−= f f De f
  • 20.
    Problem-Type 1 20 Pipe dia,D= 3 inch & L=100m Re=50,000 ʋ=1.059x10-5ft2/s (a): Laminar flow: f=64/Re=64/50,000=0.00128 ft gD fLV HLf 0357.0 )12/3)(2.32(2 )12.2)(100(00128.0 2 22 === sftV VVD /12.2 10059.1 )12/3( 50000Re 5 =⇒ × =⇒= − ν
  • 21.
    Problem-Type 1 21 Pipe dia,D= 3 inch & L=100m Re=50,000 ʋ=1.059x10-5ft2/s (b): Turbulent flow in smooth pipe: i.e.: e=0 0209.0 50000 51.2 7.3 0 log2 Re 51.2 7.3 / log2 1 =         +−=         +−= f ff De f ft gD fLV HLf 582.0 )12/3)(2.32(2 )12.2)(100(0209.0 2 22 ===
  • 22.
    Problem-Type 1 22 Pipe dia,D= 3 inch & L=100m Re=50,000 ʋ=1.059x10-5ft2/s (c): Turbulent flow in rough pipe: i.e.: e/D=0.05 0720.0 50000 51.2 7.3 05.0 log2 Re 51.2 7.3 / log2 1 =         +−=         +−= f ff De f ft gD fLV HLf 01.2 )12/3)(2.32(2 )12.2)(100(0720.0 2 22 ===
  • 23.
    Problem-Type 1 23 hL=? memDmL 0005.0;25.0;1000=== smsmQ /10306.1;/051.0 263 − ×== ν ( ) ( ) 002.025.0/0005.0/ 10210306.1/25.0039.1/ 56 == ×=××== − De VDR ν 0.0245f DiagramsMoody'From = m gD fLV hL 39.5 2 2 == smAQV /039.1/ ==Q
  • 24.
  • 25.
    Problem-Type 2 25 For laminarflow For non-laminar flow eR f 64 =         +−= f De f Re 51.2 7.3 / log2 1 Colebrook eq.
  • 26.
  • 27.
  • 28.
  • 29.
  • 30.
    MINOR LOSSES 30 Each typeof loss can be quantified using a loss coefficient (K). Losses are proportional to velocity of flow and geometry of device. Where, Hm is minor loss and K is minor loss coefficient.The value of K is typically provided for various types/devices NOTE: If L > 1000D minor losses become significantly less than that of major losses and hence can be neglected. g V KHm 2 2 =
  • 31.
    Categories of MinorLosses 31 These can be categorized as 1. Head loss due to contraction in pipe 1.1 Sudden Contraction 1.2 Gradual Contraction 2. Entrance loss 3. Head loss due to enlargement of pipe 3.1 Sudden Enlargement 3.2 Gradual Enlargement 4. Exit loss 5. Head loss due to pipe fittings 6. Head loss due to bends and elbows
  • 32.
    Minor Losses 32 Head lossdue to contraction of pipe (Sudden contraction) A sudden contraction (Figure) in pipe usually causes a marked drop in pressure in the pipe because of both the increase in velocity and the loss of energy of turbulence. g V KH cm 2 2 2 = Head loss due to sudden contraction is Where, kc is sudden contraction coefficient and it value depends up ratio of D2/D1 and velocity (V2) in smaller pipe
  • 33.
    Minor Losses 33 Head lossdue to contraction of pipe (Gradual Contraction) Head loss from pipe contraction may be greatly reduced by introducing a gradual pipe transition known as a confusor as shown Figure. g V KH cm 2 ' 2 2 = Head loss due to gradual contraction is Where, kc ’ is gradual contraction coefficient and it value depends up ratio of D2/D1 and velocity (V2) in smaller pipe
  • 34.
    Minor Losses 34 Entrance loss Thegeneral equation for an entrance head loss is also expressed in terms of velocity head of the pipe: The approximate values for the entrance loss coefficient (Ke) for different entrance conditions are given below g V KH em 2 2 =
  • 35.
    Minor Losses 35 head lossdue to enlargement of pipe (Sudden Enlargement) The behavior of the energy grade line and the hydraulic grade line in the vicinity of a sudden pipe expansion is shown in Figure The magnitude of the head loss may be expressed as ( ) g VV Hm 2 2 21 − =
  • 36.
    Minor Losses 36 head lossdue to enlargement of pipe (Gradual Enlargement) The head loss resulting from pipe expansions may be greatly reduced by introducing a gradual pipe transition known as a diffusor The magnitude of the head loss may be expressed as ( ) g VV KH em 2 2 21 − = The values of Ke’ vary with the diffuser angle (α).
  • 37.
    Minor Losses 37 Exit Loss Asubmerged pipe discharging into a large reservoir (Figure ) is a special case of head loss from expansion. ( ) g V KH dm 2 2 = Exit (discharge) head loss is expressed as where the exit (discharge) loss coefficient Kd=1.0.
  • 38.
    Minor Losses 38 Head lossdue to fittings valves Fittings are installed in pipelines to control flow.As with other losses in pipes, the head loss through fittings may also be expressed in terms of velocity head in the pipe: g V KH fm 2 2 =
  • 39.
    Minor Losses 39 Head lossdue to bends The head loss produced at a bend was found to be dependent of the ratio the radius of curvature of the bend (R) to the diameter of the pipe (D).The loss of head due to a bend may be expressed in terms of the velocity head as For smooth pipe bend of 900, the values of Kb for various values of R/D are listed in following table. g V KH bm 2 2 =
  • 40.
  • 41.
  • 42.
  • 43.
    Pipes in Series 43 Ifa pipeline is made up of lengths of different diameters, as shown in figure, conditions must satisfy the continuity and energy equations; If Q is given, the problem is straight forward. Total head loss can be estimated by adding the contributions from various sections as; νπ VD R gD LV fh D Q V L === , 2 , 4 2 2 Friction coefficient f, can be constant values given in problem or variable estimated from material and flow properties. i.e. e/D,V, R and f If head loss is given and discharge is required then either of the two methods namely equivalent velocity head method or equivalent length method many be used.;
  • 44.
    Pipes in Series 44 (1).Equivalent-velocity-head method: In this method a more accurate approach of DarcyWeisbach is applied to estimate Q. ...321 +++= LLLL hhhh Above equation considering minor losses becomes as; ... 222 2 3 3 3 3 2 2 2 2 2 2 1 1 1 1 +      ++      ++      += ∑∑∑ g V K D L f g V K D L f g V K D L fhL Now using continuity equation, we can write 3 2 31 2 12 2 21 2 1 3 2 32 2 21 2 13 2 32 2 21 2 1221 , 444 VDVDVDVD VDVDVDVDVDVDQQQ == ==⇒==⇒== πππ From above, all velocities can be expressed in terms of chosen velocity (V). (1). Equivalent velocity head method (2). Equivalent length method If Q is not given:
  • 45.
    Pipes in Series 45 (2).Equivalent length method: In this method, all pipes are expressed in terms of equivalent lengths to one given pipe size By equivalent length is meant a length, Le, of pipe of a certain diameter, De, and friction factor, fe, which for the same flow will give same head loss as the pipe under consideration of length, L, diameter, D, and friction factor, f 5 2 2 2/ 2/       == D De fe f L gVe gV D De fe f LLe
  • 46.
    Pipes in Series 46 Problem:Suppose in the Figure the pipes 1, 2, 3 are 300m of 30cm diameter, 150m of 20cm diameter and 250m of 25cm diameter, respectively, of new cast iron and are conveying 15oC water. If h=10m, find the rate of flow from A to B. Figure
  • 47.
  • 48.
  • 49.
    Pipes in Parallel 49 Inthe case of flow through two or more parallel pipes, as shown in fig, the continuity and energy equations establish the following relations which must be satisfied. According to Darcy-Weisbach equation, the head loss including minor losses can be written as; g V K D L fhL 2 2       += ∑       + = ∑K D L f gh V L2
  • 50.
    Pipes in Parallel 50 Accordingto continuity equation L L hC K D L f gh AAVQ =       + == ∑ 2 Where, C is constant for given pipe. Now according to governing equation for pipe flow, we can write as; ( ) L LLL hCCCQ hChChCQ QQQQ ... .. ... 321 221 321 +++= +++= +++= Above equations enable us to find a first estimate of hL and the distribution of flows and velocities in pipes. Using these, we can next make improvements to the values of f and if necessary repeat them until we finally make a correct determination of hL and distribution of flows.
  • 51.
    Pipes in Parallel 51 Findthe flow rates in each pipe ?
  • 52.
    Pipes in Parallel 52 Energyeq. Head loss Eq. for parallel pipes
  • 53.
  • 54.
    Problem 54 Suppose in theFigure the pipes 1, 2, 3 are 150m of 80mm diameter, 60m of 50mm diameter and 120m of 60mm diameter, respectively, of new wrough iron pipe (e=0.000046m). If hL=6m, find the rate of flow from A to B. Take kinematic viscosity as 4.26x10-5m2/s Answer: 1.5L/s
  • 55.
  • 56.
    Problem 56 In fig. pipe1 is 500ft of 2-in, pipe 2 is 350ft of 3-in, and pipe 3 is 750ft of 4- in diameter, all of smooth brass (e=0.0005ft). Crude oil (s=0.855 and kinematic viscosity of 7.6x10-5ft2/s) is flow at 0.7 cfs. Find the head loss from A to B and the flow in each pipe. Answer:
  • 57.
  • 58.
  • 59.