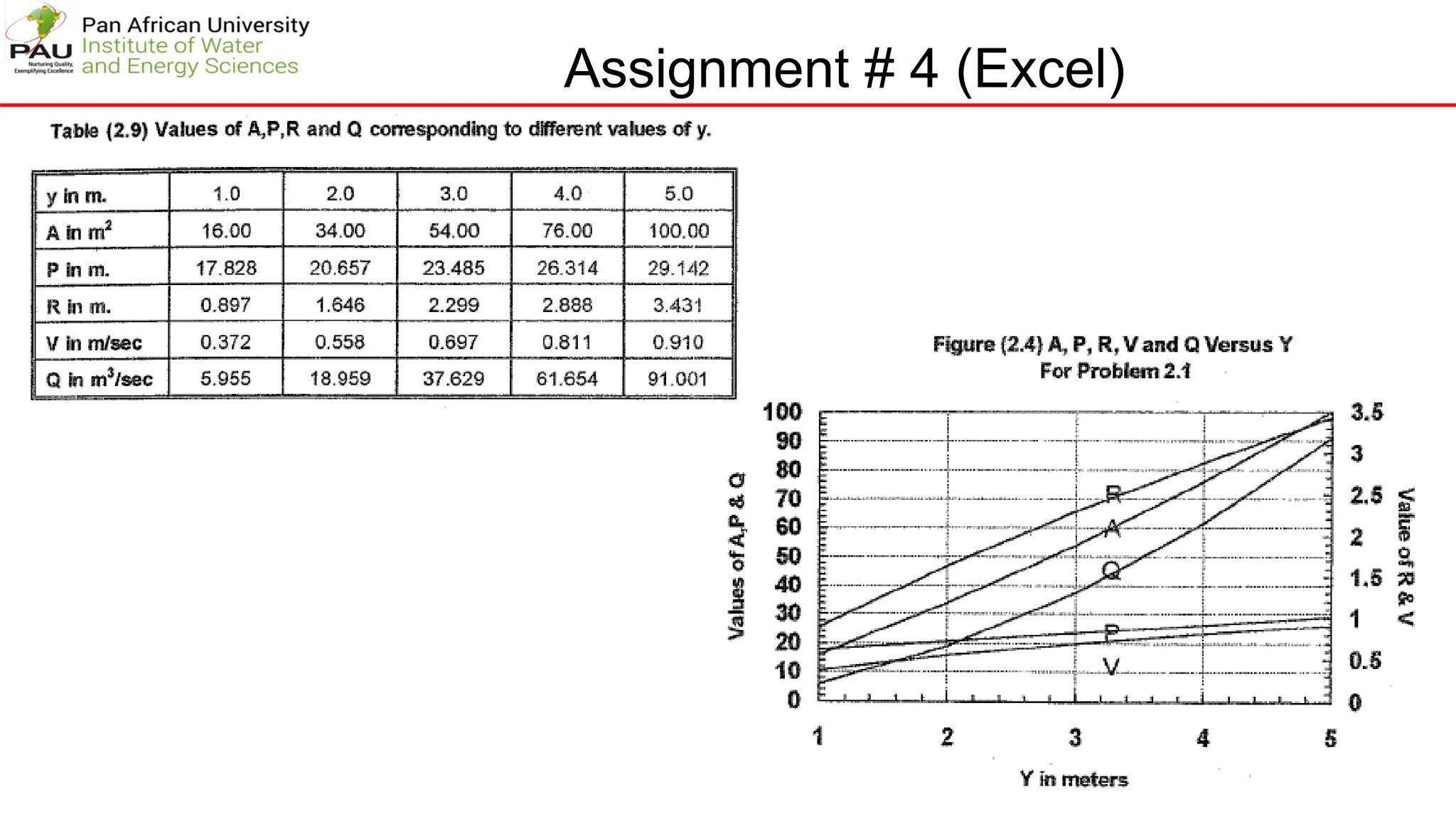
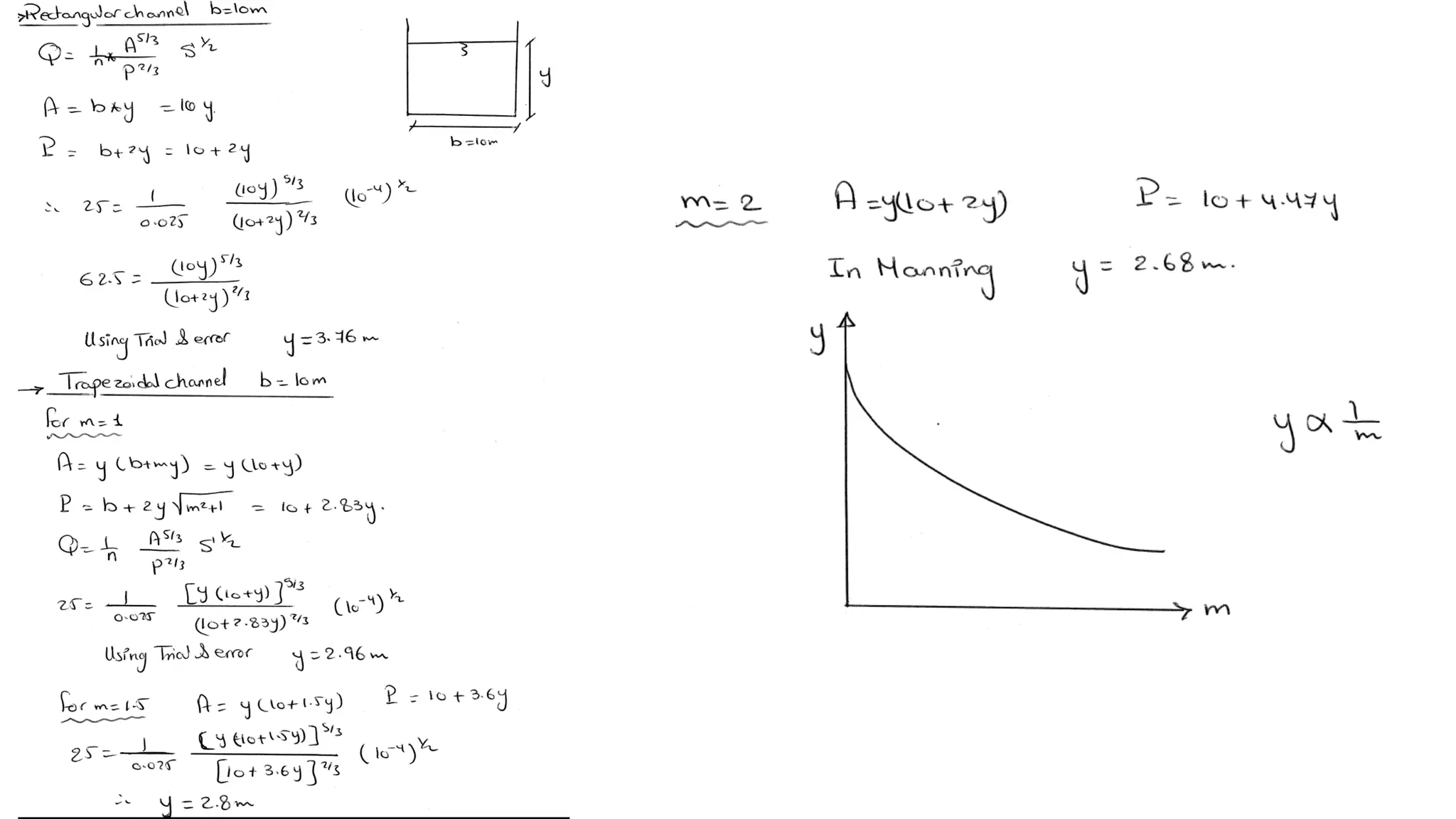
The document provides solutions to several hydraulic engineering assignments. Assignment 8 asks to find the critical slope and specific energy for a trapezoidal channel given various parameters including a Froude number of 0.12. The solution shows: 1) Using Manning's equation and the given Froude number, relationships are developed between flow rate, depth, and other variables. 2) By iterative solution, the normal flow depth is found to be 0.51m and flow rate 1.132 m3/s. 3) Similarly, the critical depth is found to be 0.125m by setting the Froude number equal to 1. 4) The critical slope is then calculated using the critical flow parameters to

1. WEUEF
Hydraulics / Advanced
Hydraulics Course
Model Answer for Assignments
Prepared by Associate Prof. Sameh KANTOUSH

2. Assignment # 2
A mercury manometer (sp. gr. = 13.6)
is used to measure the pressure
difference in vessels A and B, as
shown in the Figure. Determine the
pressure difference in pascals (N/m2).

3. Solution for Assignment # 2
The sketch of the manometer system (step 1) is shown
in Figure. Points 3 and 4 (P3, P4) are on a surface of
equal pressure (step 2) and so are the vessel A and points
1 and 2 (P1, P2):
The pressures at points 3 and 4 are, respectively (step 3),
and noting that γM = γ (sp. gr.)

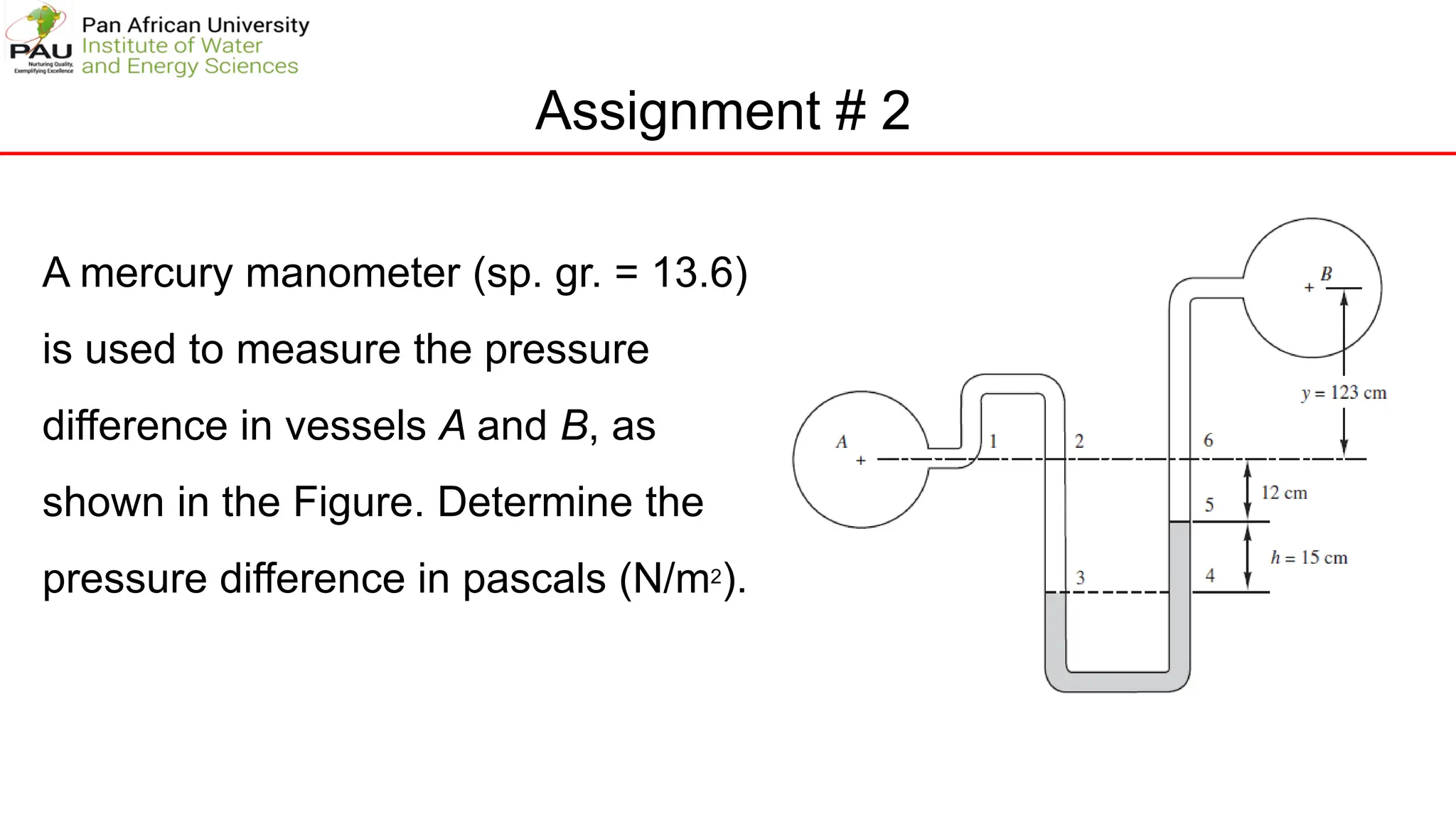
4. Assignment 3
A piezometer and a Pitot tube are tapped into a horizontal water pipe, as shown in
Figure , to measure static and stagnation (static + dynamic) pressures. For the
indicated water column heights, determine the velocity at the center of the pipe.
datum
V2=0
z1=z2=0
Solution
Bernoulli equation for section 1 and 2; datum
as shown in the Figure
[ ]
2 2
1 1 2 2
1 2
2
1 1 2
1 2 3 1 2
2 1
1
p V p V
z z
2g 2g
p V p
2g
2g (h h h ) (h h )
2g(p p )
V
+ + = + +
γ γ
+ =
γ γ
γ + + − γ +
−
= =
γ γ
1 3
V 2gh 2 9.81 0.12 1.53(m / s)
= = × × =
p2
p1

5. In Class Exercise
The bed width of a rectangular channel is 12.0 m, bed slope is 8 cm/km
and the discharge is 25 m3/sec. Considering the following two cases, draw
the T.E.L. & H.G.L. between two sections 5 km apart:
A. The flow is uniform and the water depth is 3.0 m,

6. Assignment # 4 (Excel)
Solution

7. Assignment # 4 (Excel)

8. Assignment # 5
Determine the normal water depth for each of the following open channels
if the discharge Q = 25 m3 /sec, n = 0.025, and the longitudinal bed slope
S = 10 cm/km:
A. Rectangular channel, b = 10 meters
B. Trapezoidal channel, b = 10 meters and m = 1.0, m=1.5 and m=2.
C. Draw relationship between Y & m and write your comments.

11. Assignment # 6
A rectangular canal has a bed slope of 8 cm/km, and a bed width of 100 m.
If at a depth of 6 m the canal carries a discharge of 860 m3/sec at uniform
flow. Find the roughness n, Chezy's coefficient C, and the coefficient of
friction f. Also find the average shear stress on the bed.

13. Assignment # 7
A new lined canal shall be constructed in African river basin. The maximum design
rate of flow is 100 m3/sec, the side slope is 2:1, and longitudinal bed slope is 10
cm/km. The channel is lined with concrete, for which the design Manning roughness
coefficient is 0.0182. The cost of excavation of the channel is 8 USD/m3 and the total
cost of lining is 100 USD/m2.
Determine the cost of constructing one kilometer of the channel in million USD
considering the following two cases:
(i) The bed width is four times the water depth (b=4y), and
(ii) The channel section is best hydraulic section.
Which section would you recommend? Why?

14. SOLUTION :
For a Trapezoidal channel
Given:
Qmax =100m3/s
Side Slope = 2:1 m=2
So= 10 cm/km = 0.0001
n = 0.0182
Cost of channel excavation = 8.0 USD/m3
Total cost of lining = 100.0 USD/ m2
Required: Construction cost of constructing one kilometer of the channel in million USD considering the following two cases:
(i) b=4y
(ii) Best hydraulic section.
Which section would you recommend? Why?

15. To determine:
Cost of constructing 1.0 km of the channel in million USD considering:
Case 1: The bed width, b = 4y
Flow Area of the Trapezoidal section, A= (b + my) y = (4y + 2y) y = 6y2
Wetted Perimeter of the Trapezoidal section, P = b+2y (𝑚𝑚2 + 1) = 4y +2y 22 + 1 =4y+2𝒚𝒚 𝟓𝟓 = 8.47y
Hydraulic Radius, Rh =
6y2
8.47y
= 0.7083y
From Manning’s equation: 𝑸𝑸 =
𝟏𝟏
𝒏𝒏
𝑨𝑨𝑨𝑨𝒉𝒉
𝟐𝟐
𝟑𝟑 𝑺𝑺𝒐𝒐
𝟏𝟏
𝟐𝟐
100 =
1
0.0182
∗ 6𝑦𝑦2
∗ (0.7083𝑦𝑦)
2
3 ∗ 0.0001
1
2
100= 0.54945* 6𝑦𝑦2
* 0.7946y2/3
100 = 2.6196y8/3;
38.1738 = y8/3 (38.1738)3/8 = y y = 3.92m
b=4y = 4 (3.92m) = 15.70 m (Take b = 16.0m for construction fesibility)

16. Q =100cms (> 85cms), thus free board= 0.9m
yex = y + free board
= 3.92m +0.9m = 4.82m
Design Flow Area, Aex = yex (b + myex) = 4.82 (16+ 2*4.82) = 123.58 m2
Design Wetted Perimeter, Pex = b+2yex √ (m2 +1) =16+2*4.82√5 = 16 + 21.55 = 37.55m
Cost of Channel excavation = Excavation Volume * Unit cost
= (Aex * 1000m * 8) USD = (123.58m2 *1000m* 8) USD = 988640 USD
Cost of Channel Lining = Lining Area*100 USD/m2
= Pex *L*100 = 37.55m*1000m*100 = 3,755,569 USD
Total Cost = 988640 USD + 3,755,569 USD
= 4,744,209 USD ≈ 5.0 Million USD

17. Case 2: The best hydraulic section
This is the cross-section that conveys maximum discharge for a constant cross-section area, slope and friction coefficient
Best Hydraulic section:
Qmax. → Pmin when A, n, S are constant
A= y (b + my); b=
𝐴𝐴
𝑦𝑦
– my
𝑃𝑃 = 𝑏𝑏 + 2𝑦𝑦 1 + 𝑚𝑚2
Pmin→
𝑑𝑑𝑑𝑑
𝑑𝑑𝑑𝑑
= 0
𝑑𝑑𝑑𝑑
𝑑𝑑𝑦𝑦
= 0 = -
𝐴𝐴
𝑦𝑦2 – my + 2√ (m2 + 1
𝐴𝐴
𝑦𝑦2 + m = 2 1 + 𝑚𝑚2
𝑦𝑦(𝑏𝑏 + 𝑚𝑚𝑦𝑦)
𝑦𝑦2
+ 𝑚𝑚 = 2 1 + 𝑚𝑚2 (𝑏𝑏 + 𝑚𝑚𝑦𝑦) + 𝑚𝑚𝑦𝑦 = 2𝑦𝑦 1 + 𝑚𝑚2
𝑏𝑏 + 2𝑚𝑚𝑦𝑦 + 𝑏𝑏 = 2𝑦𝑦 1 + 𝑚𝑚2 + 𝑏𝑏 2(𝑏𝑏 + 𝑚𝑚𝑦𝑦) = 𝑏𝑏 + 2𝑦𝑦 1 + 𝑚𝑚2
2𝐴𝐴
𝑦𝑦
= 𝑃𝑃
It shows that the best hydraulic trapezoidal
section has a hydraulic radius equal to one-half
of the water depth.

18. Rh =
𝒀𝒀
𝟐𝟐
Thus, when Rh =
𝒀𝒀
𝟐𝟐
Rh =
𝑭𝑭𝑭𝑭𝑭𝑭𝑭𝑭 𝑨𝑨𝑨𝑨𝑨𝑨𝑨𝑨
𝑾𝑾𝑾𝑾𝑾𝑾𝑾𝑾𝑾𝑾𝑾𝑾 𝑷𝑷𝑷𝑷𝑷𝑷𝑷𝑷𝑷𝑷𝑷𝑷𝑷𝑷𝑷𝑷𝑷𝑷
=
(b + my) y
b + 2y√ (m2
+ 1)
=
𝒚𝒚
𝟐𝟐
b= 0.472y
Manning’s equation 𝑸𝑸 =
𝟏𝟏
𝒏𝒏
𝑨𝑨𝑨𝑨𝒉𝒉
𝟐𝟐
𝟑𝟑 𝑺𝑺𝒐𝒐
𝟏𝟏
𝟐𝟐 𝑸𝑸 =
𝟏𝟏
𝒏𝒏
𝑨𝑨(
𝒚𝒚
𝟐𝟐
)
𝟐𝟐
𝟑𝟑 𝑺𝑺𝒐𝒐
𝟏𝟏
𝟐𝟐
𝑸𝑸 =
𝟏𝟏
𝒏𝒏
( (b + 2y) y )(
𝒚𝒚
𝟐𝟐
) ^(
𝟐𝟐
𝟑𝟑
)
(0.0001)
1
2 100 =
𝟏𝟏
𝟎𝟎.𝟎𝟎𝟎𝟎𝟎𝟎𝟎𝟎
( (b + 2y) y )(
𝒚𝒚
𝟐𝟐
) (
𝟐𝟐
𝟑𝟑
)
(0.0001)
1
2
100 = 0.5494 ((0.472y + 2y)*y) * (
𝒚𝒚
𝟐𝟐
) (
𝟐𝟐
𝟑𝟑
)
182.017 = 2.472y2 * (
𝒚𝒚
𝟐𝟐
) (
𝟐𝟐
𝟑𝟑
)
y = 5.96m b=0.472y = 0.472*(5.96) = 2.814m ( Take b = 3.0m)
yex= 5.96 m+ 0.9m= 6.86m
Design Flow Area, Aex = yex (b + myex) = 6.86 (3+ 2*6.86) = 114.699 m2
Design Wetted Perimeter, Pex = b+2yex √ (m2 +1) = 3+2*6.86√5 = 3 +30.8577 = 33.678m
Cost of Channel excavation = Excavation Volume * Unit cost
= (Aex * 1000m * 8) USD = (114.699 m2 *1000m* 8) USD = 917592 USD
Cost of Channel Lining = Lining Area*100 USD/m2
= Pex *L*100 = 33.678m *1000m*100 = 3,367,800 USD
Total Cost = 917592 + 3,367,800 = 4,285,392 USD = 4.00 Million USD
The calculations show that he best
hydraulic trapezoidal section has less
cost comparing to the other method with
higher hydraulic performance.

19. Assignment #8
Water is flowing in a trapezoidal channel of bed width = 8.0 m,
longitudinal bed slope = 12 cm/km, side slopes are 1:1,
Manning roughness coefficient = 0.025. If the Froude number
= 0.12, find the critical slope and specific energy.
Solution
Given:
Cross section: Trapezoidal Channel
B = 8.0m
So= 12 cm/km = 0.00012
Side Slopes m=1
Manning’s roughness coefficient, n = 0.025
Froude Number, Fr = 0.12 (<1) i.e. Sub-Critical Flow (Mild Slope where yn > yc)
A= (b + my) y = (8+y) y =8*y +y2
P = b+2y√ (m² +1) = 8+2*y*√2
T = b+2y = 8+2*y

20. 𝑆𝑆𝑐𝑐 =
𝑛𝑛𝑛𝑛
𝐴𝐴𝑐𝑐𝑅𝑅ℎ𝑐𝑐
2/3
2
𝑄𝑄2 =
0.1413 × 8𝑦𝑦+𝑦𝑦2 3
8+2𝑦𝑦
(1)
𝐹𝐹𝑟𝑟
2
=
𝑄𝑄2
𝑔𝑔𝐴𝐴3
𝑇𝑇
From Manning’s equation; to determine
the relationship between Q and Yn
𝑄𝑄2 =
0.192 × 8𝑦𝑦+𝑦𝑦2
10
3
(8+2𝑦𝑦√2)
4
3
(2)
From equations (1) and (2)
0.7359 =
8𝑦𝑦+𝑦𝑦2
1
3 × (8+2𝑦𝑦)
(8+2.828𝑦𝑦)
4
3
By trail and errors yn
= 0.51 m and Q = 1.132 m3/s
𝑄𝑄2
𝑔𝑔𝐴𝐴𝑐𝑐
3 𝑇𝑇𝑐𝑐 = 1 𝑜𝑜𝑜𝑜
𝑄𝑄2
𝑔𝑔
=
𝐴𝐴𝑐𝑐
3
𝑇𝑇𝑐𝑐
0.130 =
(8∗𝑦𝑦𝑐𝑐+𝑦𝑦𝑐𝑐
2 )3
8+2𝑦𝑦𝑐𝑐
By trail and errors yc
= 0.125 m
𝑆𝑆𝑐𝑐 =
0.025 ∗ 1.132
1.024 ∗ 0.1222/3
2
𝑆𝑆𝑐𝑐 = 0.0125

21. 𝐸𝐸 = 𝑦𝑦 +
𝑄𝑄2
2𝑔𝑔𝐴𝐴2
𝐸𝐸 = 0.51 +
1.281
369.572
= 0. 𝟓𝟓𝟓𝟓𝟓𝟓 m
At yn
= 0.51 and Q = 1.132 m3/s
A = 8𝑦𝑦 + 𝑦𝑦2 = ((8*0.51) + 0.512) = 4.08 + 0.2601 = 4.34 m2

24. ً‫ا‬‫ﺷﻛر‬
Vielen Dank
Thank you for your attention
ありがとうございます