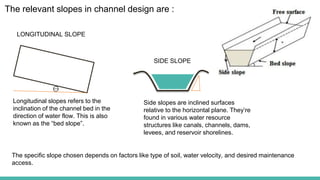
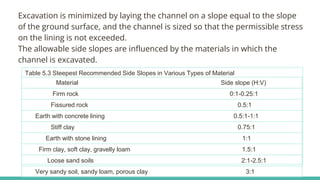
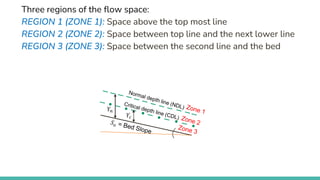
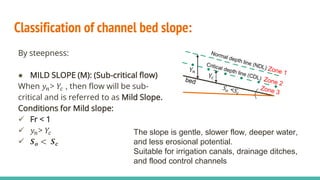
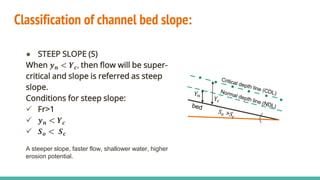
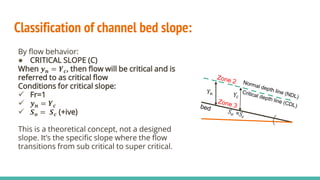
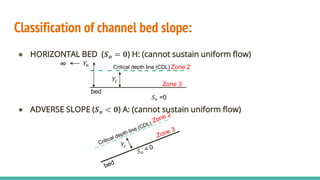
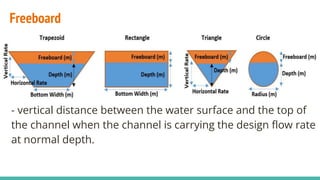
The document discusses channel slope and freeboard design in waterways, highlighting key factors like the inclination of channel beds, stability concerns, and soil characteristics. It outlines the classification of slopes (mild, steep, and critical) and emphasizes the importance of freeboard to prevent overflow and ensure safety. Additionally, it provides guidelines for designing channels suitable for various applications such as irrigation, drainage, and flood control, along with sample problems illustrating the calculations involved.

1. CHANNEL SLOPE &
FREEBOARD
GROUP 5

2. WHAT IS CHANNEL SLOPE ?
• Refers to the inclination of a channel, typically a streambed or a
man made waterway in the direction of water flow. It is
essentially the steepness of the channel bed as it travels from a
higher elevation to a lower one.
• Can be expressed as a ratio (rise over run) or a percentage.

3. SIDE SLOPE
⊖
LONGITUDINAL SLOPE
The relevant slopes in channel design are :
Longitudinal slopes refers to the
inclination of the channel bed in the
direction of water flow. This is also
known as the “bed slope”.
Side slopes are inclined surfaces
relative to the horizontal plane. They’re
found in various water resource
structures like canals, channels, dams,
levees, and reservoir shorelines.
The specific slope chosen depends on factors like type of soil, water velocity, and desired maintenance
access.

4. Excavation is minimized by laying the channel on a slope equal to the slope
of the ground surface, and the channel is sized so that the permissible stress
on the lining is not exceeded.
The allowable side slopes are influenced by the materials in which the
channel is excavated.
Table 5.3 Steepest Recommended Side Slopes in Various Types of Material
Material Side slope (H:V)
Firm rock 0:1-0.25:1
Fissured rock 0.5:1
Earth with concrete lining 0.5:1-1:1
Stiff clay 0.75:1
Earth with stone lining 1:1
Firm clay, soft clay, gravelly loam 1.5:1
Loose sand soils 2:1-2.5:1
Very sandy soil, sandy loam, porous clay 3:1

5. The design of longitudinal slope considers various factors like:
• Water flow velocity: steeper slope result in faster water flow which can be
beneficial for increasing the channel’s flow capacity (the amount of water it
can convey).
• Channel stability: Steeper slopes can exert higher forces on the channel bed
and banks increasing the risk of erosion and collapse.
• Soil characteristic: The type of soil the channel will be built in plays a crucial
role. Soils with higher cohesion (clay) can handle steeper slopes compared to
loose soil (sand) that require flatter slopes for stability.
• Manning’s roughness coefficient (n): This coefficient accounts for the
friction between the water and the channel beds and walls. A rougher channel
(e.g., with vegetation or uneven surfaces) will have a higher manning’s n
value, requiring a steeper slope to achieve the same flow velocity compared
to a smoother channel. (𝑛 = 𝑅2/3
𝑆𝑓1/2
/ v)

6. The design of side slope considers various factors like:
● Stability: the slope angle needs to be stable enough to withstand the forces
exerted by water and soil weight
● Erosion control: the slope design should minimize erosion from water flow
and wave action
● Maintenance access: in some cases, the side slope needs to allow for access
for maintenance or inspection purposes
● Water depth: The expected water depth in the channel needs to be
considered. Steeper slopes can accommodate deeper water depths, but they
may not be stable for shallow water flow.

7. Importance of channel slope in different water ways
● Irrigation canals- channel slope is carefully designed to ensure adequate
water delivery to fields while minimizing erosion and energy losses.
● Flood control channels- steeper slopes can convey large flood flows
quickly, but require robust bank protection measures.
● Drainage channels- slopes are designed to efficiently remove excess
water from an area, considering factors like soil type and drainage
requirements
● Hydropower canals- slopes are tailored to achieve the desired water
velocities for efficient power generation in turbines.

8. General Importance of channel slope
● Affects water velocity: steeper slopes lead to faster flow, potentially
causing erosion
● Influence flow capacity: steeper slopes allow for higher flow rates
● Impacts channel stability: excessive slope can lead to bank erosion and
channel failure.

9. Flow Profiles
Water surface profile- measure of how the flow
depth changes longitudinally. The profiles are
classified based on the relationship between the
actual water depth (y), normal water depth (𝑦𝑛), and
the critical depth (𝑦𝑐).
• In a channel, there are two fixed depths:
(1) 𝒚𝒏= normal depth of flow – occur if flow is
uniform and steady (Manning’s equation)
(2) 𝒀𝒄= critical depth of flow- depth of flow where
energy is at a minimum for a particular
discharge
𝑌𝑛
𝑌𝑐

10. Froude Number (Fr): Fr=
𝑽
𝒈𝒉
This dimensionless number describes the ratio of inertial forces (due to
velocity) to gravitational forces acting on the flow.
Fr < 1: Subcritical Flow
Fr = 1: Critical Flow
Fr> 1: Supercritical Flow
Flow profiles are classified by the slope of the channel (𝑆𝑜), 𝑌𝑛, and
𝑌𝑐. There are five classifications designated by the letters M, S, C, H,
and A (Mild, Steep, Critical, Horizontal and Adverse)

11. Three regions of the flow space:
REGION 1 (ZONE 1): Space above the top most line
REGION 2 (ZONE 2): Space between top line and the next lower line
REGION 3 (ZONE 3): Space between the second line and the bed
𝑌𝑛
𝑌𝑐

12. Classification of channel bed slope:
By steepness:
● MILD SLOPE (M): (Sub-critical flow)
When 𝑦𝑛> 𝑌𝑐 , then flow will be sub-
critical and is referred to as Mild Slope.
Conditions for Mild slope:
 Fr < 1
 𝑦𝑛> 𝑌𝑐
 𝑺𝒐 < 𝑺𝒄
The slope is gentle, slower flow, deeper water,
and less erosional potential.
Suitable for irrigation canals, drainage ditches,
and flood control channels
𝑌𝑛
𝑌𝑐

13. Classification of channel bed slope:
● STEEP SLOPE (S)
When 𝒚𝒏 < 𝒀𝒄, then flow will be super-
critical and slope is referred as steep
slope.
Conditions for steep slope:
 Fr>1
 𝒚𝒏 < 𝒀𝒄
 𝑺𝒐 < 𝑺𝒄
𝑌𝑛
𝑌𝑐
A steeper slope, faster flow, shallower water, higher
erosion potential.

14. Classification of channel bed slope:
By flow behavior:
● CRITICAL SLOPE (C)
When 𝒚𝒏 = 𝒀𝒄, then flow will be critical and is
referred to as critical flow
Conditions for critical slope:
 Fr=1
 𝒚𝒏 = 𝒀𝒄
 𝑺𝒐 = 𝑺𝒄 (+ive)
This is a theoretical concept, not a designed
slope. It’s the specific slope where the flow
transitions from sub critical to super critical.
𝑌𝑛 𝑌𝑐

15. Classification of channel bed slope:
SUB CRITICAL FLOW: This is dominated by gravitational forces and behaves in a slow or
stable way. It has a Froude number less than 1.
(actual depth>critical depth)
SUPER CRITICAL FLOW: Dominated by inertial forces and behaves as rapid or unstable flow.
Supercritical flow transitions to subcritical through a hydraulic jump which represents a high
energy loss with erosive potential. Behaves faster and shallower. Fr >1. (actual depth<critical
depth)
CRITICAL FLOW : Transition that possesses the minimum possible energy for that flow rate.
Fr = 1.
CRITICAL SLOPE -is the reference point for understanding flow behavior and potential issues
like hydraulic jumps (sudden changes in water depth) that can occur during flow transitions.

16. Classification of channel bed slope:
● HORIZONTAL BED (𝑺𝒐 = 𝟎) H: (cannot sustain uniform flow)
● ADVERSE SLOPE (𝑺𝒐 < 𝟎) A: (cannot sustain uniform flow)
Critical depth line (CDL)
Zone 3
Zone 2
𝑌𝑐
𝑌𝑛
∞
bed
𝑌𝑐
𝑆𝑜 =0

17. SAMPLE PROBLEM
The discharge in a rectangular channel of width 6m with Manning’s n=0.012 is
24 cubic meter/s. if the streamwise slope is 1:200 find:
a. Normal water depth (Yn)
b. Froude number @ Yn
c. Critical depth (Yc)
*State whether the normal flow is sub-critical or super-critical.

18. SAMPLE PROBLEM
A channel of trapezoidal section, 2m wide at the base with side sloping 45°
with the horizontal. This channel carries water at rate of 6 cubic meter/s. Find
the following:
a. Critical depth (Yc)
b. Type of flow if Y=1m
c. Compute Fr if Yn=1.2m

19. Freeboard
- vertical distance between the water surface and the top of
the channel when the channel is carrying the design flow rate
at normal depth.

20. Freeboard
Purposes:
Freeboard is provided to account for the uncertainty in the design,
construction, and operation of the channel.
• Prevent overflows from wind-driven waves
• Protects against erosion
• Ensures safety
• Superelevation of flow around bends
• Extra channel capacity

21. Freeboard and Superelevation

22. Freeboard
● Lined channel
FB- freeboard
Y- depth of flow
C- coefficient. C=1.5 for Q ≤ 20 cfs (0.57cu.m/s)
C= 2.5 for Q ≥ 3000 cfs (85cu.m/s)
Or use C= 0.01184Q+1.493
FB=
0.55 𝑪𝒚
0.15 m, y < 0.30 m
0.30 m, y ≥ 0.30 m, V ≤ 1.72 m/s

23. Freeboard
● Unlined channel
FB- freeboard
Y- depth of flow
C- coefficient. C=1.5 for Q ≤ 20 cfs (0.57cu.m/s)
C= 2.5 for Q ≥ 3000 cfs (85cu.m/s)
Or use C= 0.01184Q+1.493
FB=
𝑪𝒚
0.15 m, y < 0.30 m
0.30 m, y ≥ 0.30 m, V ≤ 1.72 m/s

24. Freeboard
GENERAL CRITERION:
The freeboard must be sufficient to prevent waves or fluctuations in the
water surface from overflowing to the sides. Commonly used criterion is that
the height of freeboard should at least be equal to the velocity head plus
15cm (6 in), hence
FB= 0.15 +
𝑽𝟐
𝟐𝒈
0.15 m, y < 0.30 m
0.30 m, y ≥ 0.30 m, V ≤ 1.72 m/s
F= 0.15 +
𝑽𝟐
𝟐𝒈
m, y ≥ 0.30 m, V ≥1.72 m/s
FB=

25. Freeboard
For channels on steep slopes, it is also recommended that the freeboard
should be greater than the flow depth (USFHWA, 2005) to account for high
variations of swift flow by waves, surges, and splashes. In general, linings
should extend to at least the freeboard elevation.
At channel bends, additional freeboard must be provided to accommodate
the superelevation (𝒉𝒔) of the water surface.
𝒉
𝒔=
𝑽𝟐𝑻
𝒈𝒓𝒄
V- average velocity in the channel
T- top width of the channel
- radius of curvature of the centerline of the channel.
𝑟𝑐

26. Freeboard
 Freeboard is a hedge against overtopping the channel and it is always
advisable to ensure there is freeboard in an installation.
 In general, the recommended amount of freeboard is 1/6 of the channel
depth- this typically allows to provide enough room so that wave action or
flow surges don’t overtop the channel.

27. SAMPLE PROBLEM
Design a reinforced concrete (n=0.015) “best” trapezoidal channel to carry 2.4
𝒎𝟑
𝒔
where the land surface slope is 0.5%. The ‘tightest’ turn anticipated will
have a radius of 5m.
GIVEN:
n= 0.015
Q= 2.4
𝒎𝟑
𝒔
S=0.005
● 𝒓𝒄 = 𝟓 𝒎

28. SAMPLE PROBLEM
1) SOLVE FOR VALUE OF Y (FLOW DEPTH)
2) SOLVE FOR VALUE OF V (VELOCITY)
3) SOLVE FOR FREEBOARD
4) SOLVE FOR SUPERELEVATION IF 𝒓𝒄 is 5m
5) SOLVE FOR THE FINAL VALUE OF Y

29. GROUP 5 – BSCE 4B
GAMBOA, KATE B.
DOMALLIG, GENESIS RYMS B.
NGAO-I, GERALDINE B.
PASCUA, JENIFER D.
TACLAWAN, ARIEL B.
DULAGAN, AUBREY C.
BANGGUIYAC, JANELE P.