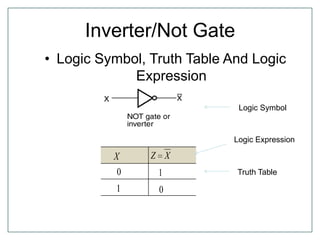
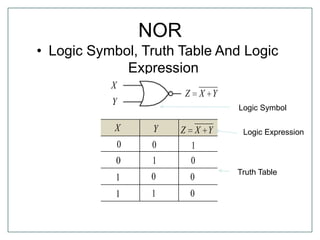
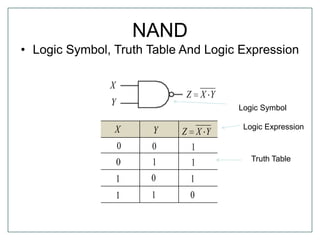
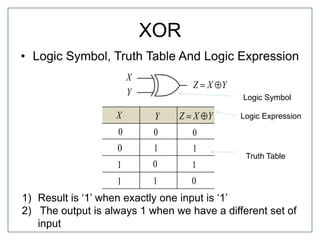
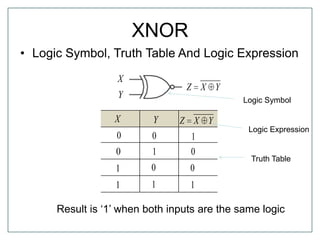
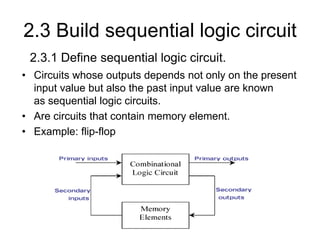
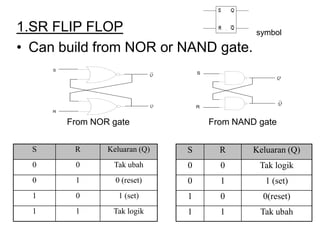
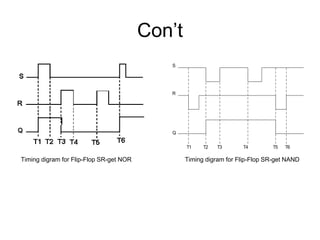
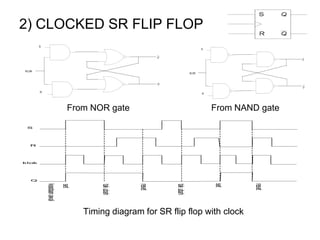
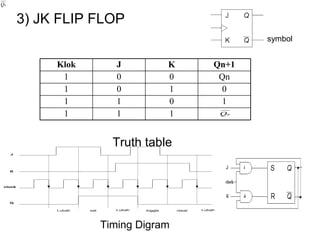
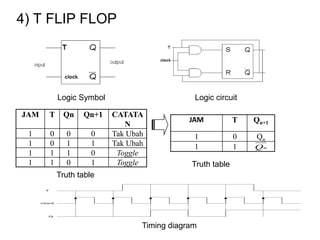
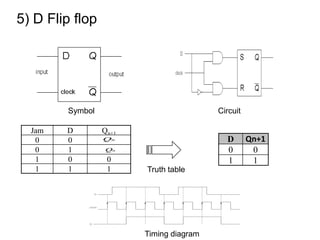
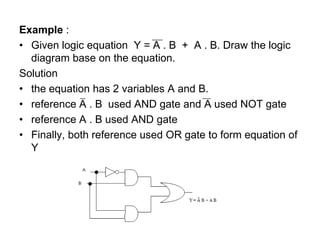
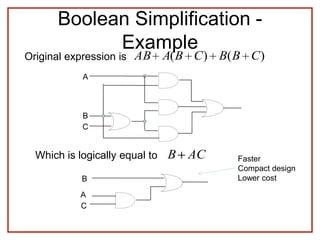
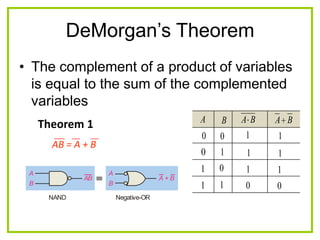
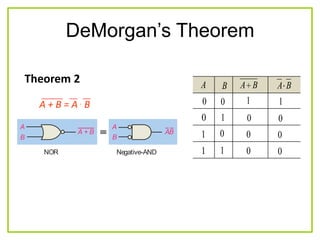
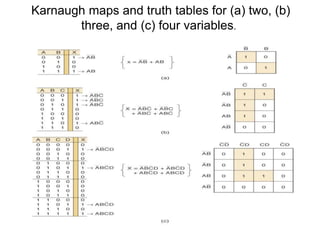
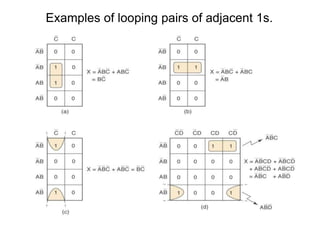
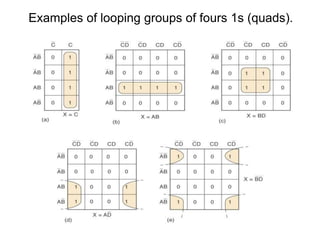
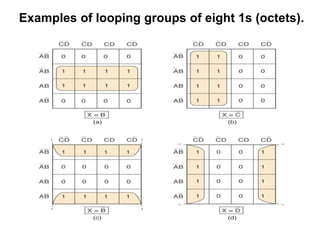
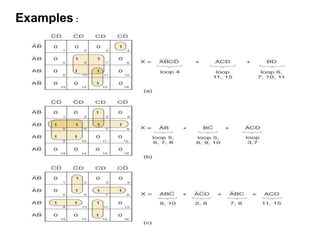
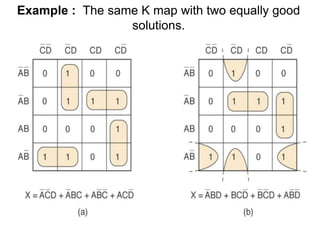
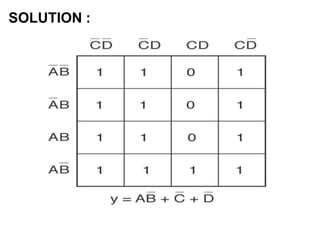
The document discusses Boolean algebra and logic gates. It defines logic gates, explains their operations, and provides their logic symbols and truth tables. The types of logic gates covered are AND, OR, NOT, NOR, NAND, XOR, and XNOR. It also discusses sequential logic circuits like flip-flops, providing details on SR, JK, T, and D flip-flops including how to build them using logic gates. Additional topics covered include the difference between combinational and sequential logic circuits, Boolean theorems, sum-of-products and product-of-sums expressions, and the Karnaugh map method for simplifying logic expressions.

1. 2.2 PERFORM
OPERATION WITH
BOOLEAN ALGEBRA

2. 2.2.1 Define logic gates
• A logic gate performs a logical operation
on one or more logic inputs and produces
a single logic output and most commonly
found at digital circuits.

3. 2.2.2 Explain the operation of logic gates.
2.2.3 Draw logic symbols for gates.
2.2.4 Construct truth table of logic gates.

4. AND Gate
• Logic Symbol, Truth Table And Logic
Expression
YXZX
0 0
10
Y
01
11
0
0
0
1
Logic Symbol
Truth Table
Logic Expression

5. OR Gate
• Logic Symbol, Truth Table And Logic
Expression
YXZX
0 0
10
Y
01
11
0
1
1
1
Logic Symbol
Truth Table
Logic Expression

6. Inverter/Not Gate
• Logic Symbol, Truth Table And Logic
Expression
XZX
0 1
01
Logic Symbol
Truth Table
Logic Expression

7. NOR
• Logic Symbol, Truth Table And Logic
Expression
YXZX
0 0
10
Y
01
11
1
0
0
0
YXZ
X
Y
Logic Symbol
Truth Table
Logic Expression

8. NAND
• Logic Symbol, Truth Table And Logic Expression
YXZX
0 0
10
Y
01
11
1
1
1
0
YXZ
X
Y Logic Symbol
Truth Table
Logic Expression

9. XOR
• Logic Symbol, Truth Table And Logic Expression
YXZX
0 0
10
Y
01
11
0
1
1
0
YXZ
X
Y
1) Result is „1‟ when exactly one input is „1‟
2) The output is always 1 when we have a different set of
input
Logic Symbol
Truth Table
Logic Expression

10. XNOR
• Logic Symbol, Truth Table And Logic Expression
YXZX
0 0
10
Y
01
11
1
0
0
1
YXZ
X
Y
Result is „1‟ when both inputs are the same logic
Logic Symbol
Truth Table
Logic Expression

11. 2.3 Build sequential logic circuit
• Circuits whose outputs depends not only on the present
input value but also the past input value are known
as sequential logic circuits.
• Are circuits that contain memory element.
• Example: flip-flop
2.3.1 Define sequential logic circuit.

12. 2.3.2 Differentiate between combinational logic
circuit and sequential logic circuit
• Combinational Logic Circuit –
refers to circuits whose output is strictly
depended on the present value of the inputs.
Example: logic gates
• Sequential Logic Circuit-
Circuits whose outputs depends not only on
the present input value but also the past input
value are known as sequential logic circuits.
Example: flip-flop

13. 2.3.3 Describe Flip Flop
• Is a logic circuit that has two stable states
or memory where one state is compliment
with other state.
• can be divided into common types either
synchronous(clock) or asynchronous (no
clock):

14. 2.3.4 List the types of flip-flop:
a. SR flip – flop (SR- set reset)
b. Clocked SR flip – flop
c. JK flip – flop
d. T flip flop (Toggle)
e. D flip flop (Delay or Data)

15. 2.3.5 Build SR, JK, T and D flip flop
using logic gates.
2.3.6 Draw the symbol and truth
table of SR, JK, T and D flip –flop.

16. 1.SR FLIP FLOP
• Can build from NOR or NAND gate.
From NOR gate From NAND gate
S
R
Q
Q
S
R
Q
Q
S R Keluaran (Q)
0 0 Tak logik
0 1 1 (set)
1 0 0(reset)
1 1 Tak ubah
S R Keluaran (Q)
0 0 Tak ubah
0 1 0 (reset)
1 0 1 (set)
1 1 Tak logik
symbol

17. Con‟t
Timing digram for Flip-Flop SR-get NOR Timing digram for Flip-Flop SR-get NAND
S
R
Q
T1 T2 T3 T4 T5 T6

18. 2) CLOCKED SR FLIP FLOP
From NOR gate From NAND gate
Timing diagram for SR flip flop with clock
S
KLOK
R
Q
Q
S
KLOK
R
Q
Q
S
R
klok
Q
keadaanawal
set
takubah
reset
reset
takubah
set

19. 3) JK FLIP FLOP
Truth table
Timing Digram
nQ
J
K
clock
Q
t.ubah set t.ubah toggle reset t.ubah
Klok J K Qn+1
1 0 0 Qn
1 0 1 0
1 1 0 1
1 1 1 nQ
symbol

20. 4) T FLIP FLOP
JAM T Qn Qn+1 CATATA
N
1 0 0 0 Tak Ubah
1 0 1 1 Tak Ubah
1 1 1 0 Toggle
1 1 0 1 Toggle
JAM T Qn+1
1 0 Qn
1 1 nQ
T
clock
Q
Logic Symbol Logic circuit
Truth table
Truth table
Timing diagram

21. 5) D Flip flop
Jam D Qn+1
0 0
0 1
1 0 0
1 1 1
nQ
nQ D Qn+1
0 0
1 1
D
clock
Q
Symbol Circuit
Truth table
Timing diagram

22. COMBINATIONAL LOGIC CIRCUIT
• refers to circuits whose output is strictly
depended on the present value of the inputs
• Are made of logic gates with no feedback.
• To design combinational logic circuit, we need to
know about basic logic equation :
– If sign “+” between two or more variables, it
means all variables using OR gate. For
example : A + B + C
– If sign “.” between two or more variables, it
means all variables using AND gate
operation. For example : A.B.C

23. Example :
• Given logic equation Y = A . B + A . B. Draw the logic
diagram base on the equation.
Solution
• the equation has 2 variables A and B.
• reference A . B used AND gate and A used NOT gate
• reference A . B used AND gate
• Finally, both reference used OR gate to form equation of
Y

24. Boolean Theorem
• Basic Rules
1. A + 0 = A
2. A + 1 = 1
5. A . 0 = 0
6. A . 1 = A
3. A + A = A
7. A . A = A
4. A + A = 1
8. A . A = 0
9. A = A
=
10. A + AB = A
12. (A + B)(A + C) = A + BC
11. A + AB = A + B

25. BOOLEAN THEOREMS
XXX
X
XX
XX
XXX
X
X
.7
11.6
0.5
0.4
.3
X1.2
00.1
XZWZXYWYZYXWb
XZXYZYXa
XYZZXYYZX
ZYXZYXZYX
XYYX
XYYX
XX
.13
.13
.12
.11
.10
.9
1.8
AA
YXXY
YXYX
YXYXX
XXYX
.18
.17
.16
.15
.14

26. Boolean Simplification -
Example
• Using Boolean theorem, Simplify the
expression:
)()( CBBCBAAB
• Apply distributive law,
BCBBACABAB
• Apply rule 7 (BB = B), and rule 5 (AB + AB = AB)
BACAB
• Apply rule 10 (B + BC = B)
BCBACAB

27. Boolean Simplification -
Example
BACAB
• Apply rule 10 (AB + B = B)
ACB
At this point, the expression is simplified as much
as possible
Original expression is )()( CBBCBAAB
Which is logically equal to ACB
In terms of design, what is the advantage of
Boolean simplification?

28. Boolean Simplification -
Example
Original expression is )()( CBBCBAAB
Which is logically equal to ACB Faster
Compact design
Lower cost
A
B
C
A
B
C

29. DeMorgan‟s Theorem
• The complement of a product of variables
is equal to the sum of the complemented
variables
AB = A + B
A + B
A
B
AB
A
B
NAND Negative-OR
BAA
0 0
10
B
01
11
1
1
1
0
BA
1
1
1
0
Theorem 1

30. DeMorgan‟s Theorem
BAA
0 0
10
B
01
11
1
0
0
0
BA
1
0
0
0
Theorem 2
AB
A
B
A + B
A
B
NOR Negative-AND
A + B = A . B

31. Example 1:
• Given Z = A + B . C .Simplified the equation
below using De‟ Morgan Theorem.
Solution;
Z = A + B.C
= A . B.C
= A .( B+C)
= A . (B+C)

32. Example 2:
• Given Z = (A + C).(B+D) .Simplified the
equation below using De‟ Morgan Theorem.
Solution :
Z = (A + C) . (B + D)
= (A + C) + (B + D)
= (A . C) + (B . D)
= AC + BD

33. Sum-of-Products
• SOP expressions consist of two or more AND
terms (products) that are ORed together
• In SOP an inversion cannot cover more than
one variable in a term
Example:
• ABC + ABC
• A B + A B + A B
• A B C + A B C
• A B + A B C + C D + C

34. Product-of-Sums
• POS expressions consist of two or more
OR terms (sums) that are ANDed together
• Example:
– X = (A + B + C)(A + C)
– X = (A + B)(C + D)F
– X = ( A + B ) . ( B + C )
– X = ( B + C + D ) . ( B C + E )
– X = ( A + C ) . ( B + E ). ( C + B )

35. Karnaugh Map Method
• A graphical method of simplifying logic
equations or truth tables.
• Also called a K map.
• Theoretically can be used for any number
of input variables, but practically limited to
5 or 6 variables.

36. Karnaugh Map Method
• The truth table values are placed in the
K map.
• Adjacent K map square differ in only
one variable both horizontally and
vertically.
• The pattern from top to bottom and left
to right must be in the form
• A SOP expression can be obtained by
ORing all squares that contain a 1.

37. Karnaugh Map Method
• Looping adjacent groups of 2, 4, or 8 1s will
result in further simplification.
• When the largest possible groups have been
looped, only the common terms are placed in
the final expression.
• Looping may also be wrapped between top,
bottom, and sides.
• Looping a pair (or quad or octet and so on) of
adjacent 1s in a K map eliminates the variable
that appears in complemented and
uncomplemented form.

38. Karnaugh maps and truth tables for (a) two, (b)
three, and (c) four variables.

39. Examples of looping pairs of adjacent 1s.

40. Examples of looping groups of fours 1s (quads).

41. Examples of looping groups of eight 1s (octets).

42. Karnaugh Map Method
• Complete K map simplification process
– Construct the K map, place 1s as indicated in the truth
table.
– Loop 1s that are not adjacent to any other 1s. (Isolated
1s)
– Loop 1s that are in pairs
– Loop 1s in octets even if they have already been
looped.
– Loop quads that have one or more 1s not already
looped. (Use minimum number of loops)
– Loop any pairs necessary to include 1s not already
looped.
– Form the OR sum of terms generated by each loop.

43. Examples :

44. Example : The same K map with two equally good
solutions.

45. Example :
• Use a K map to simplify:
Y = C(ABD + D) + ABC + D

46. SOLUTION :