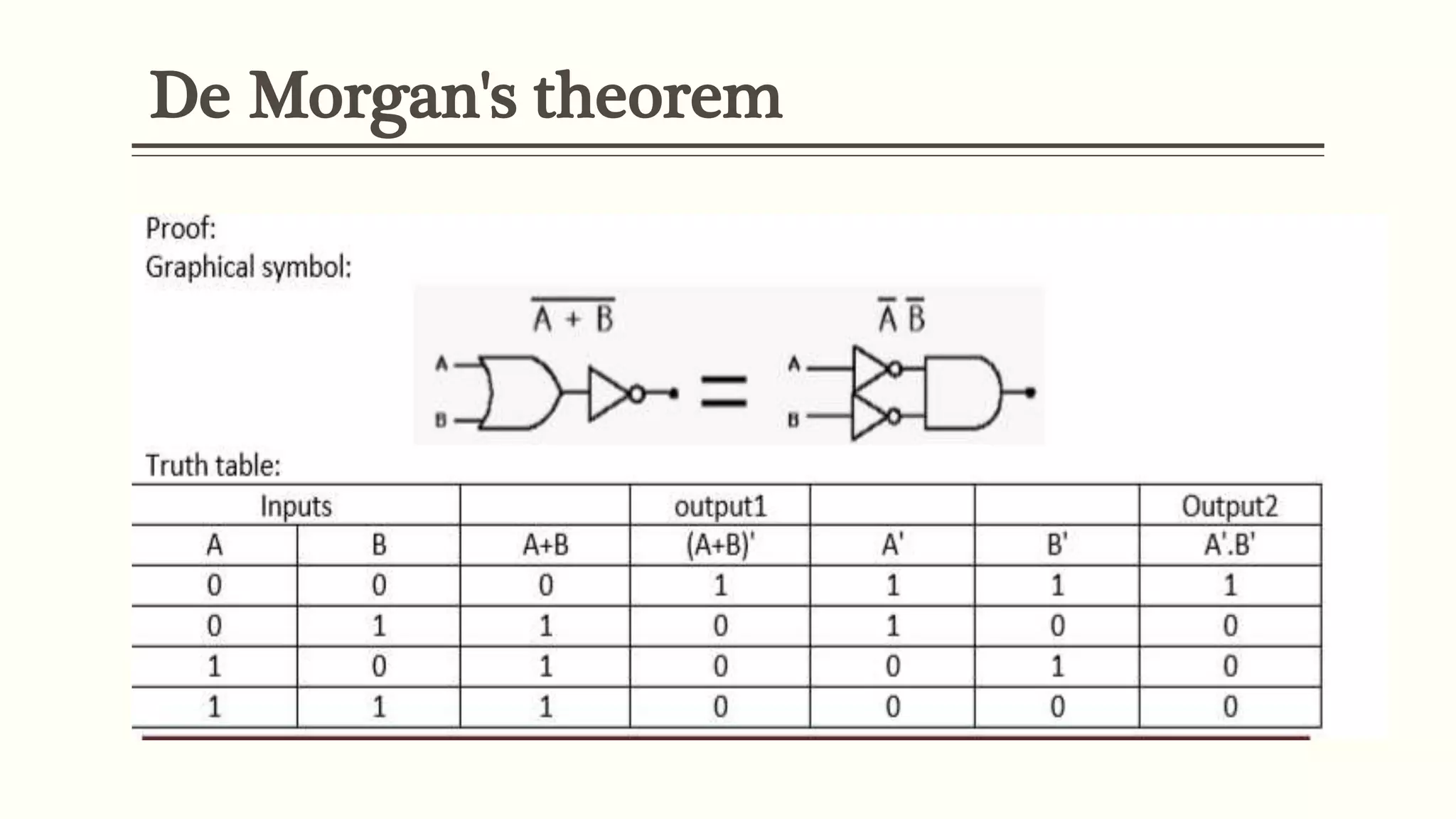
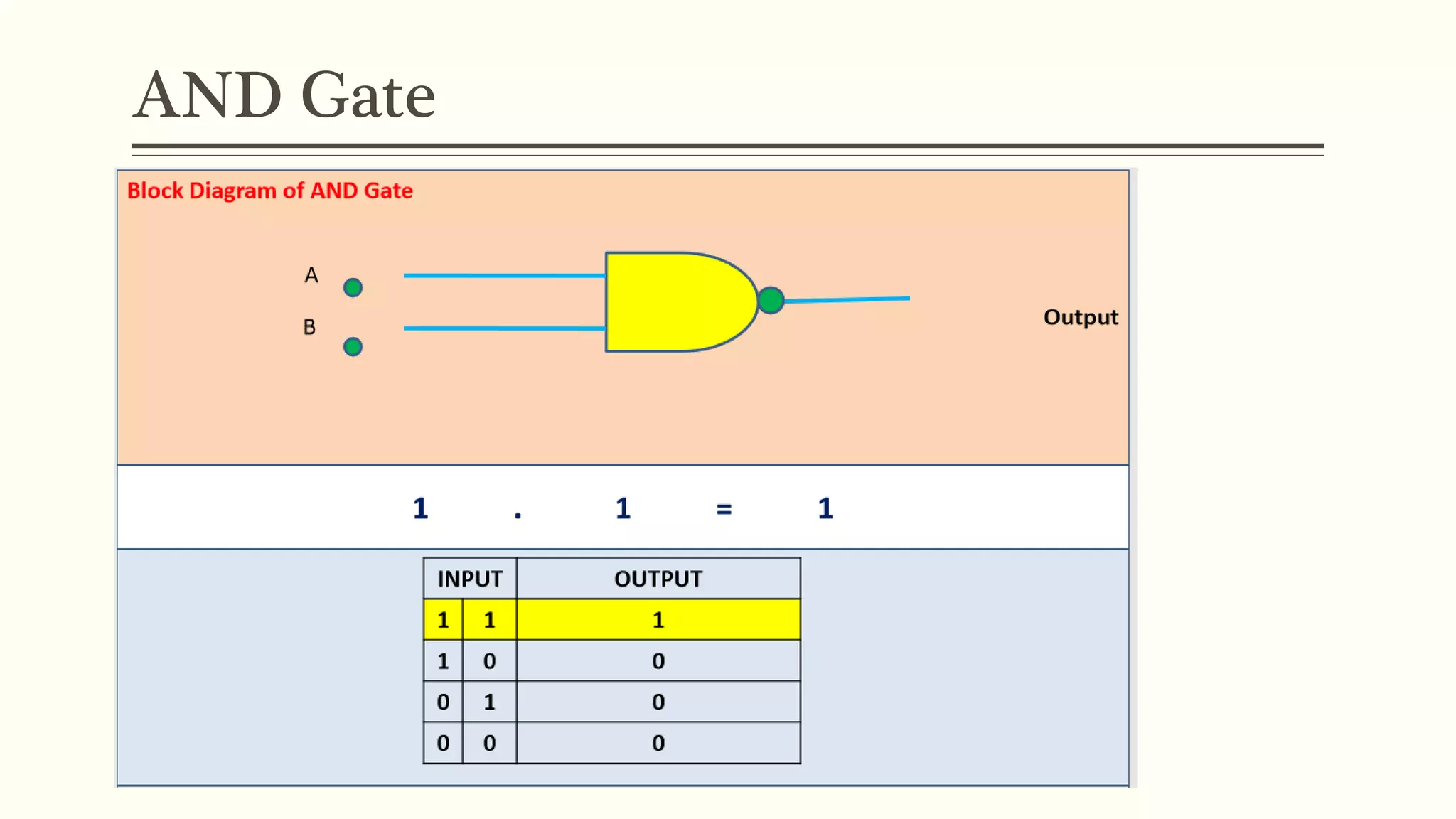
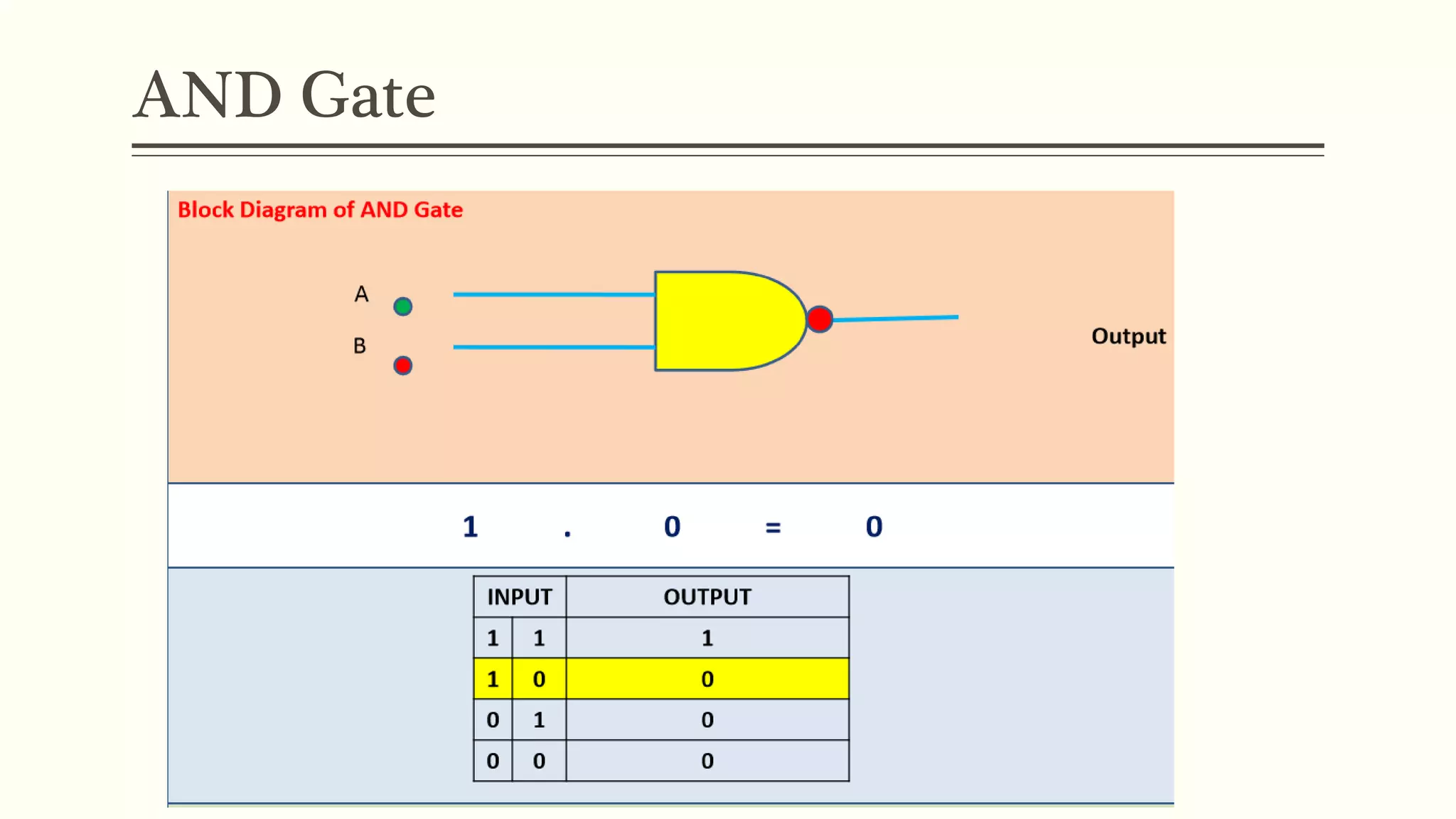
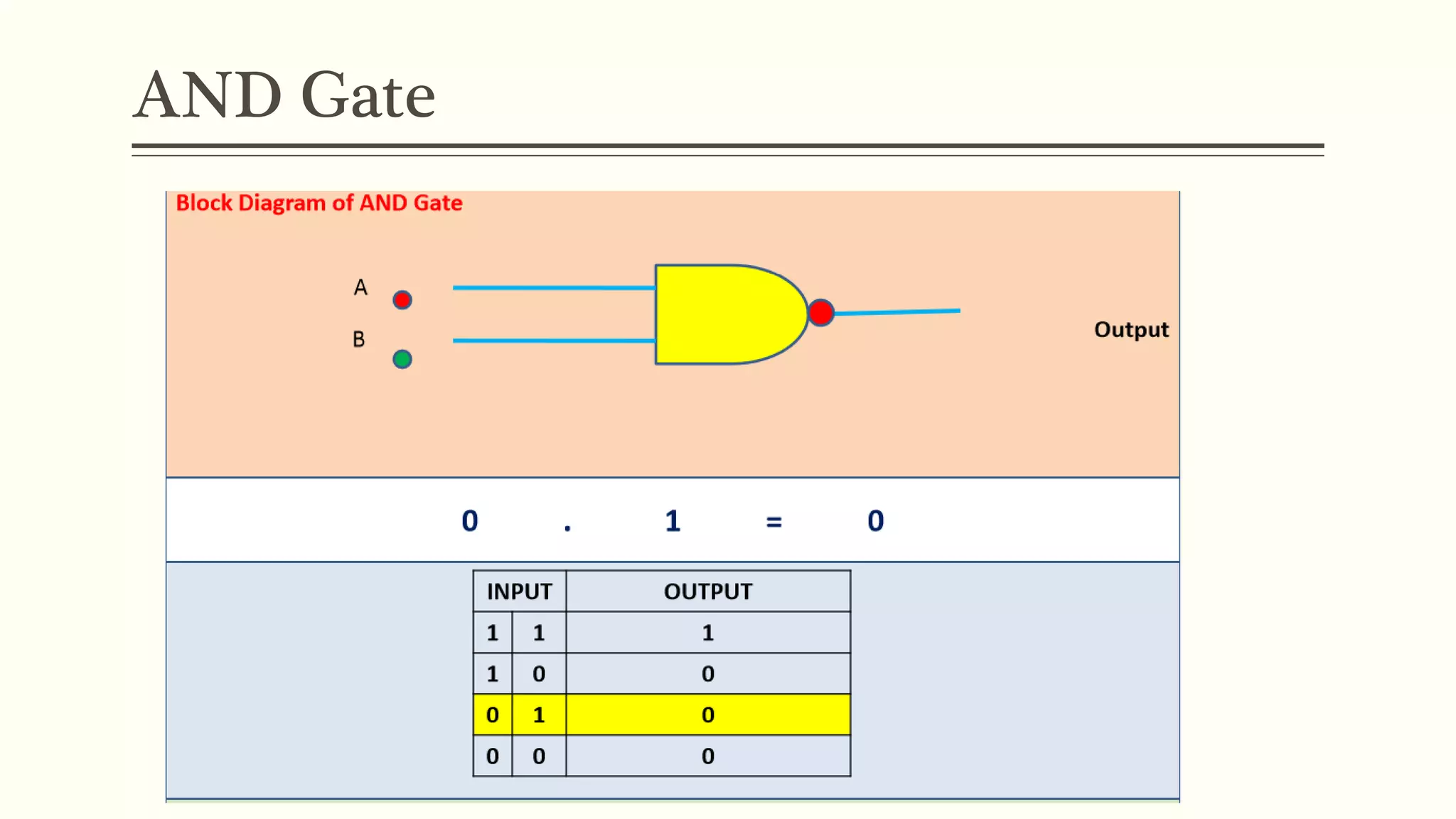
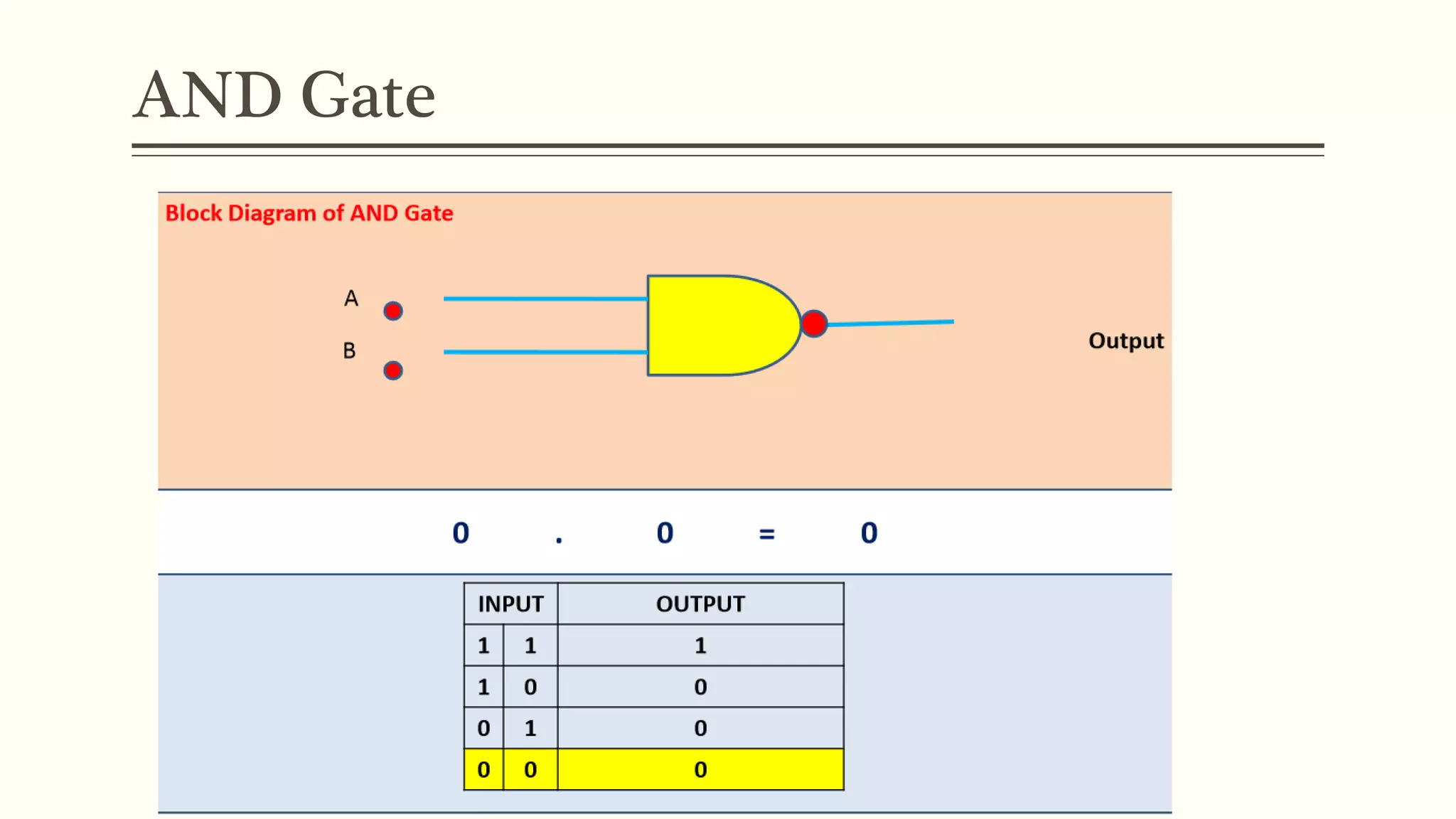
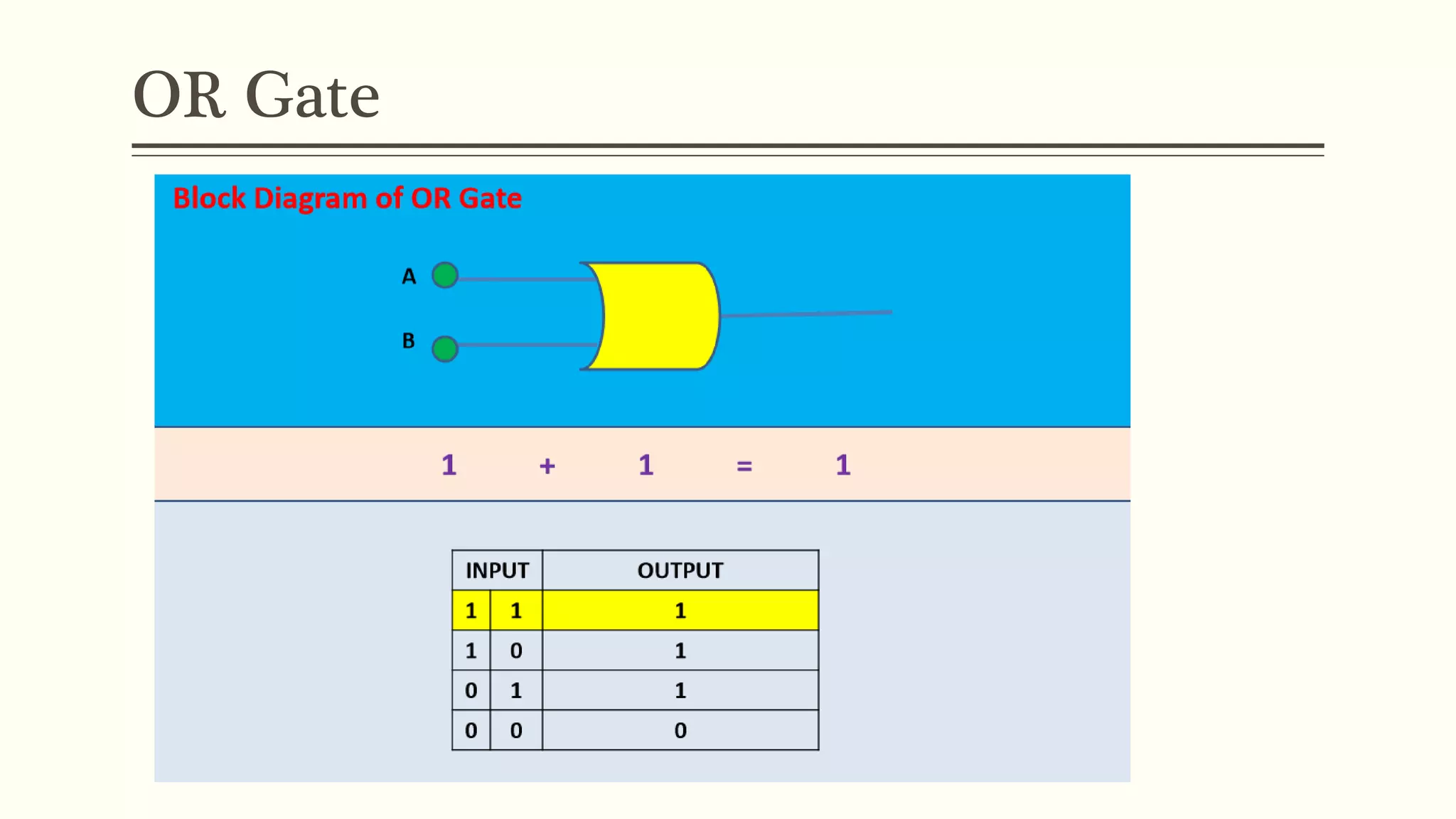
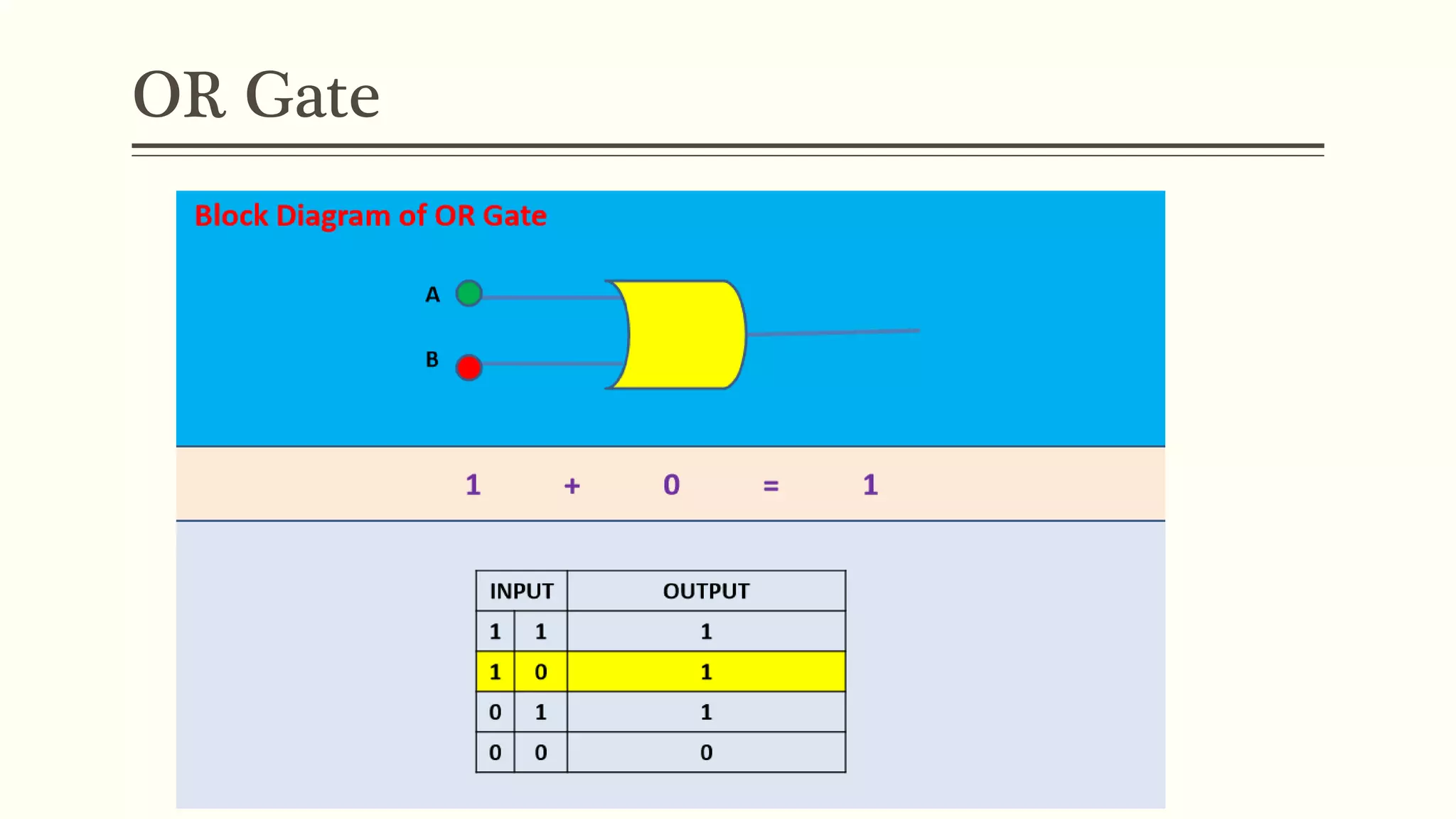
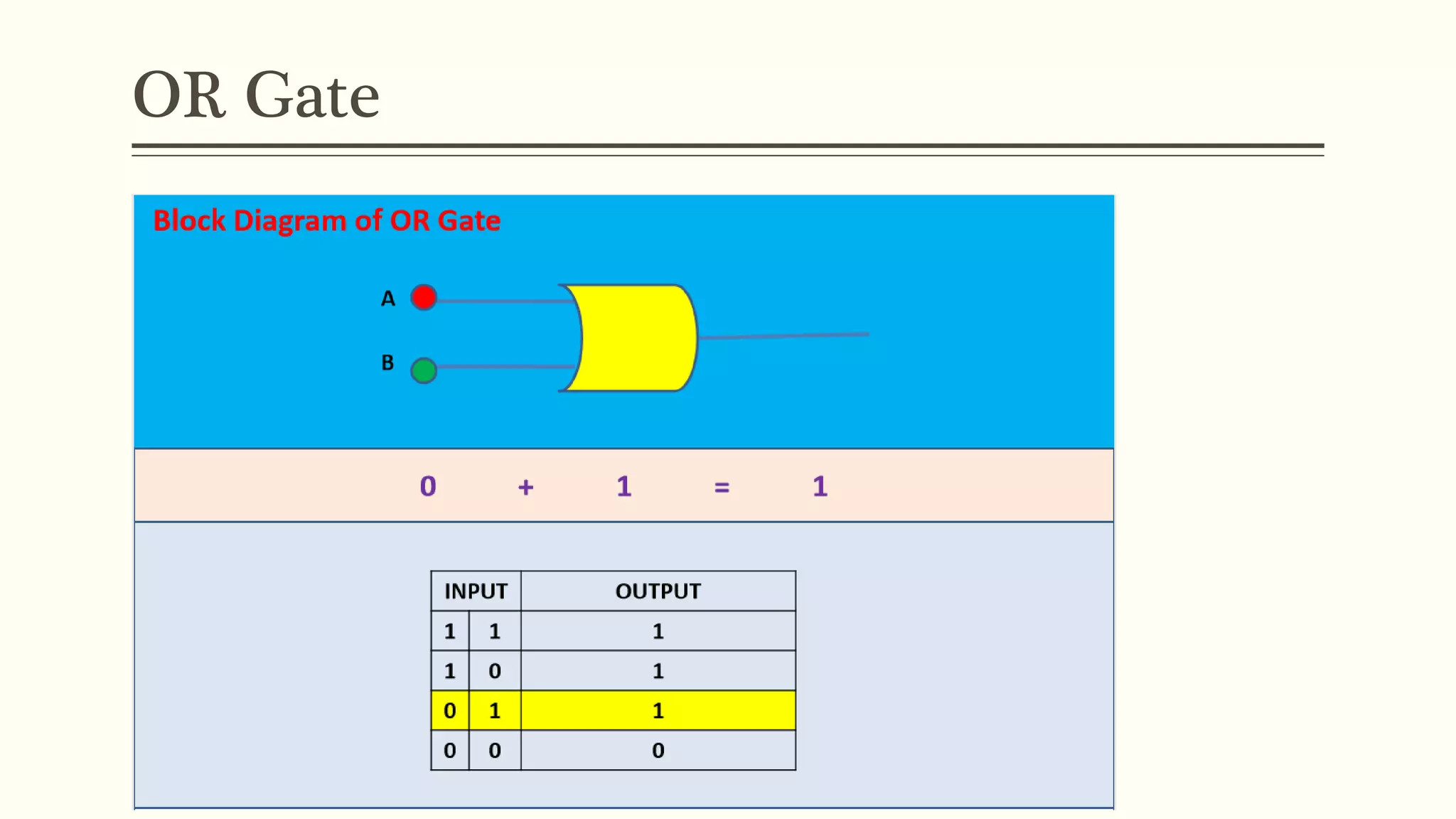
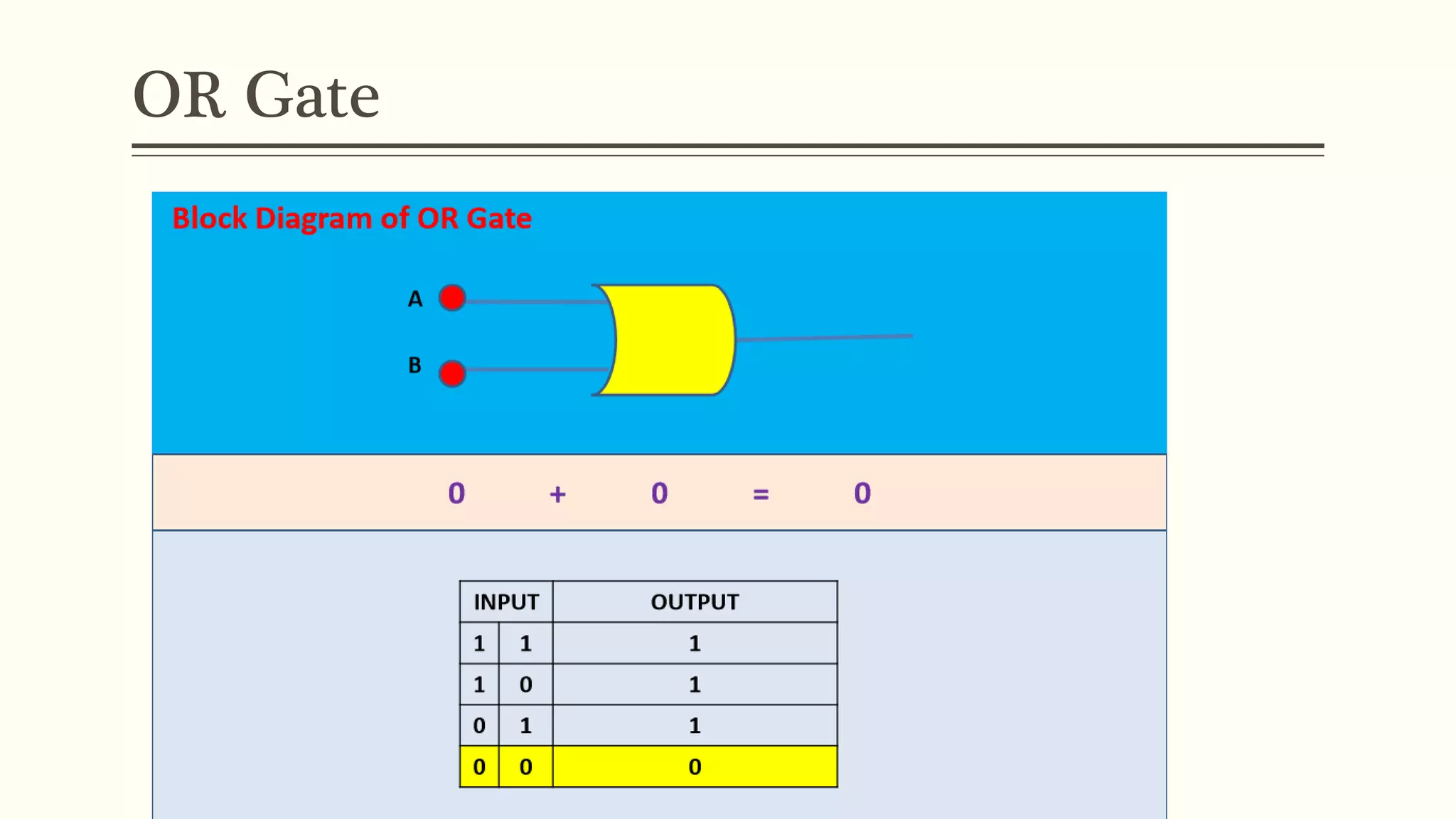
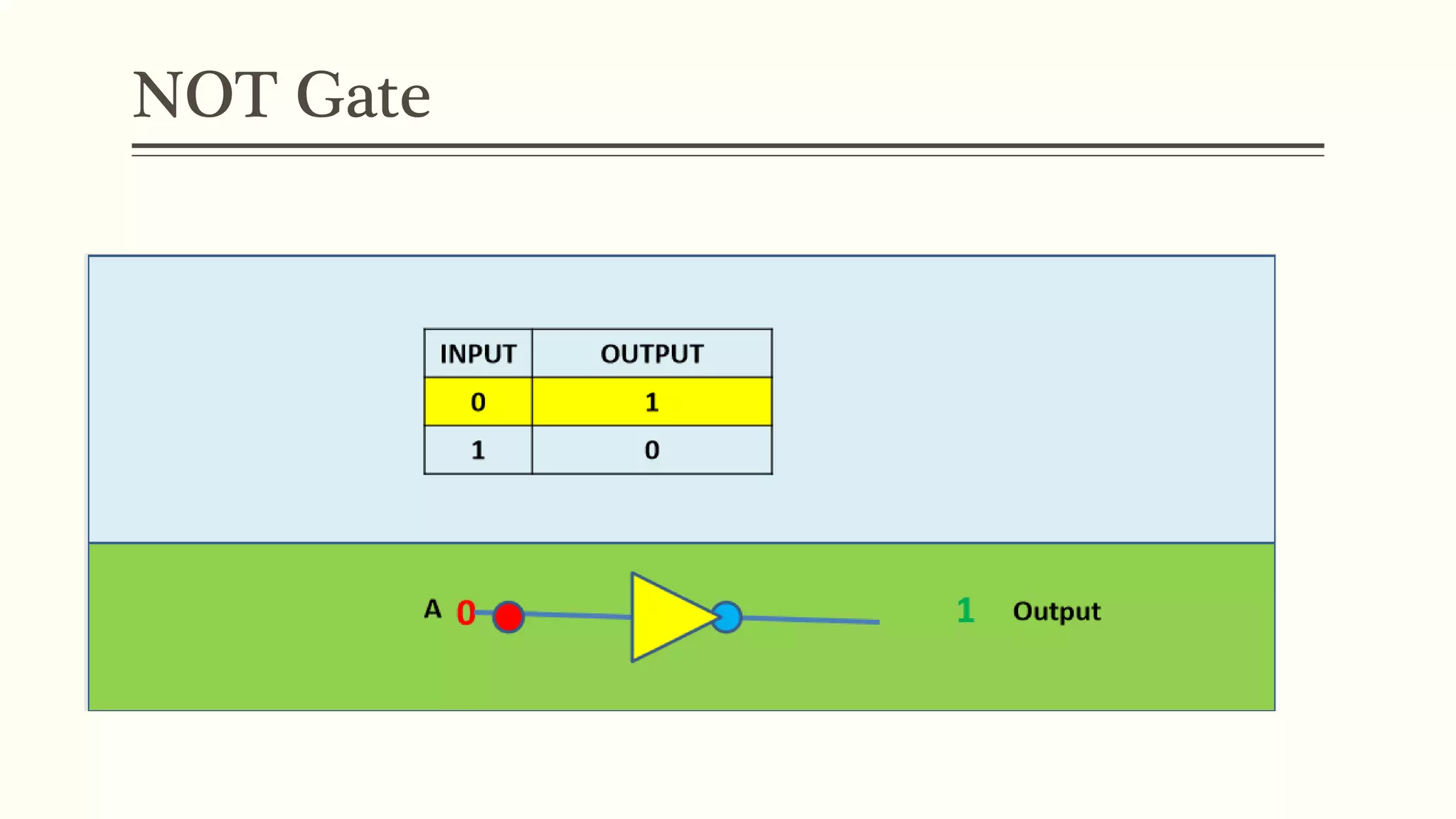
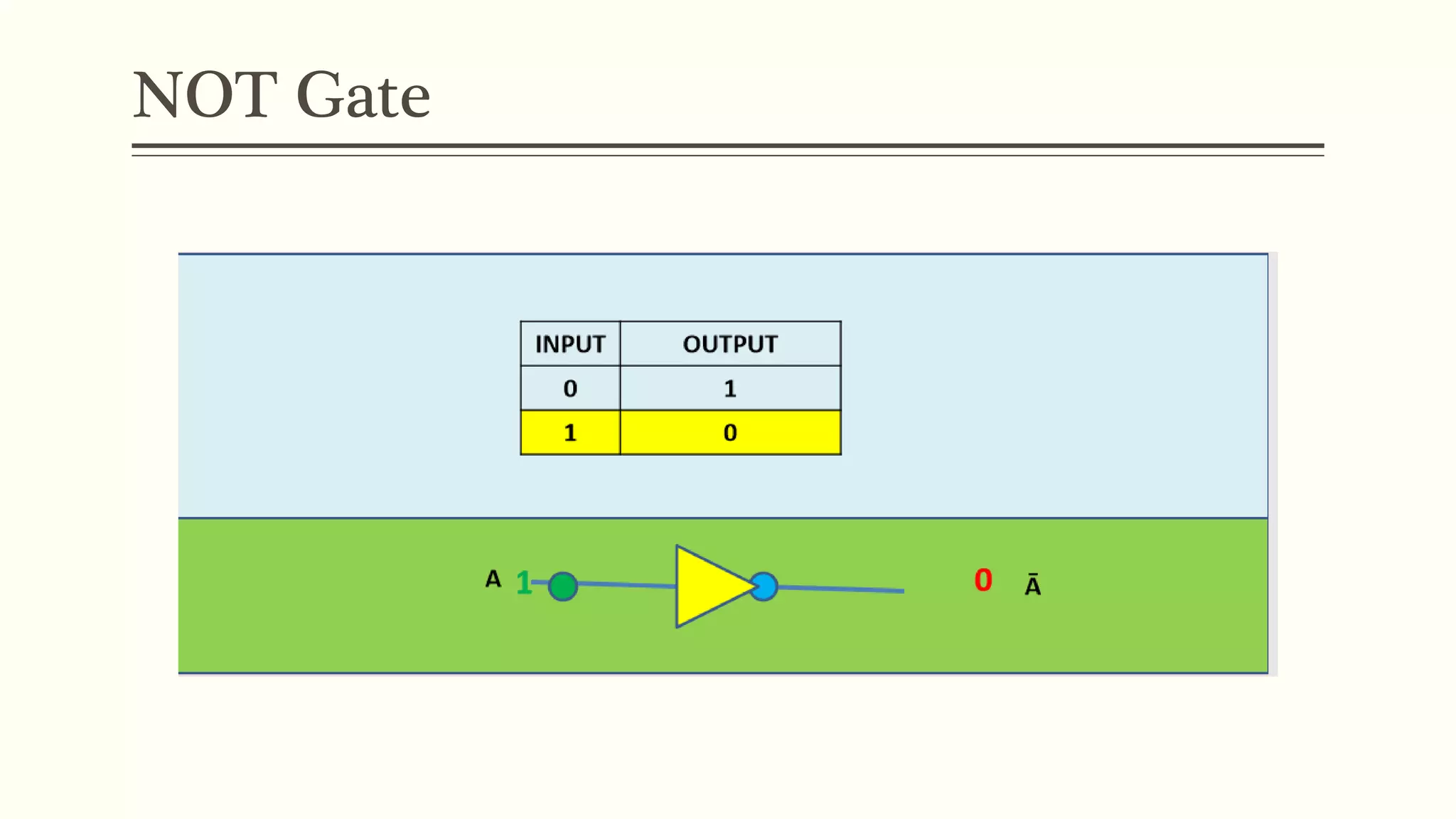
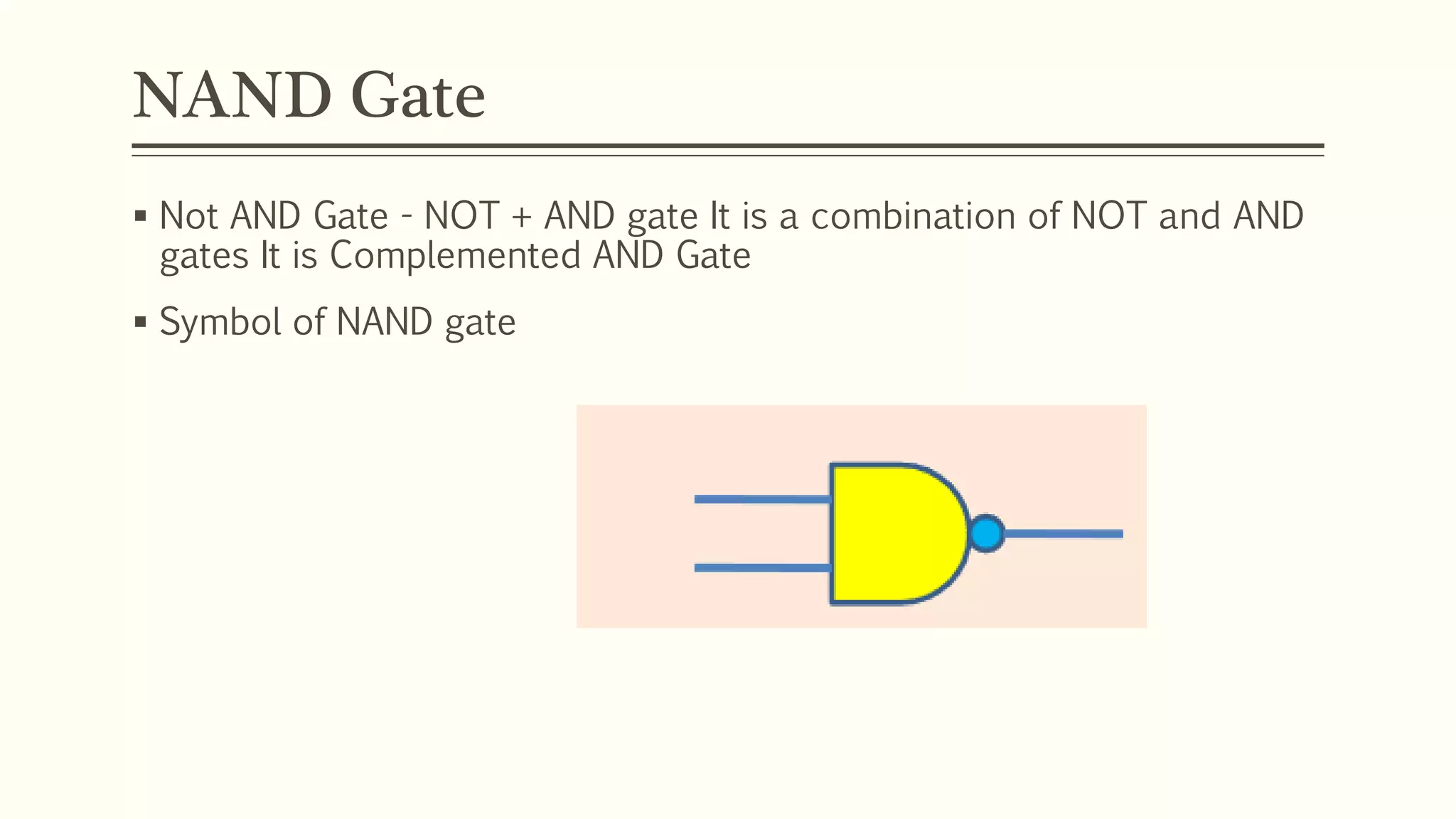
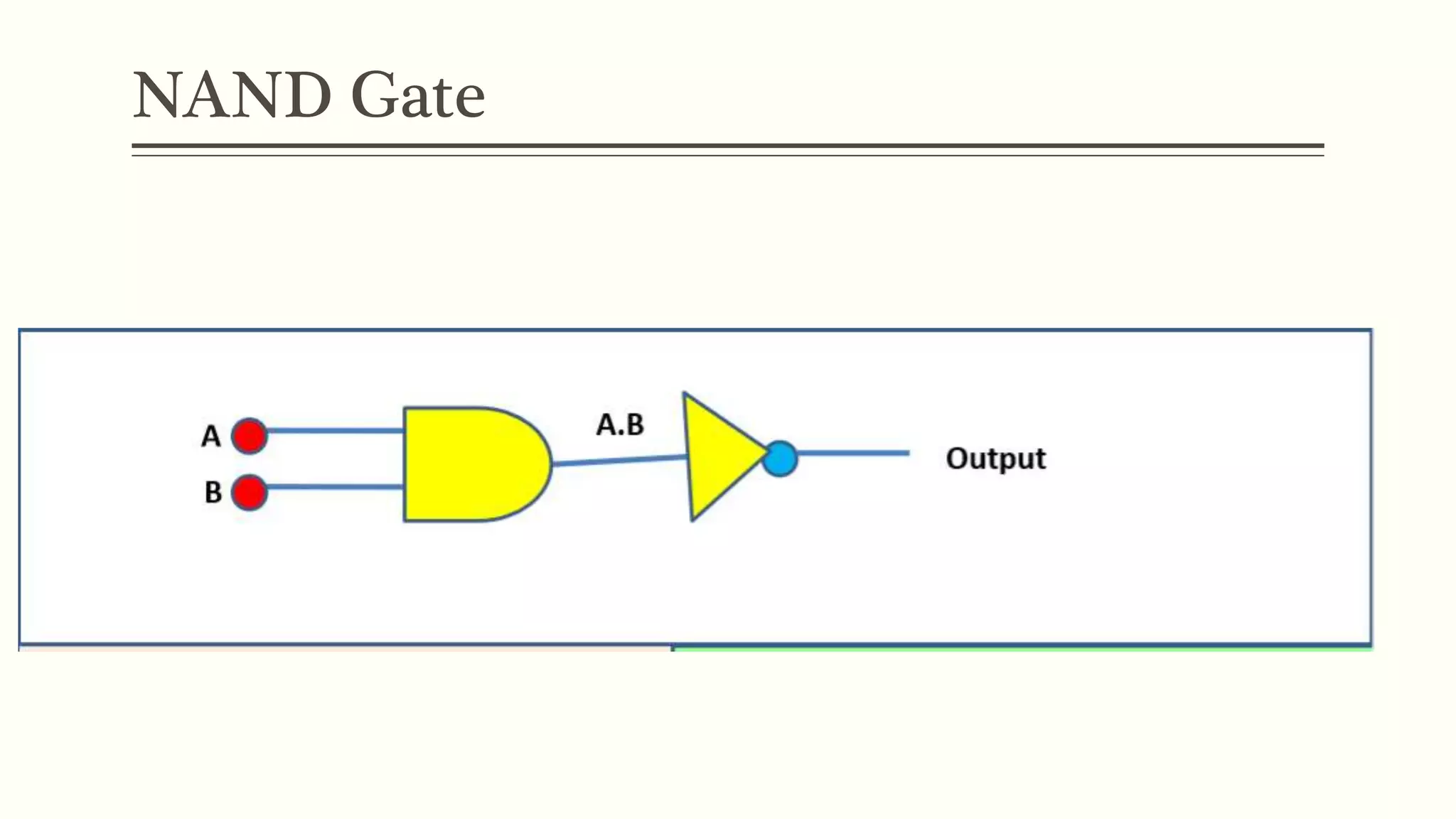
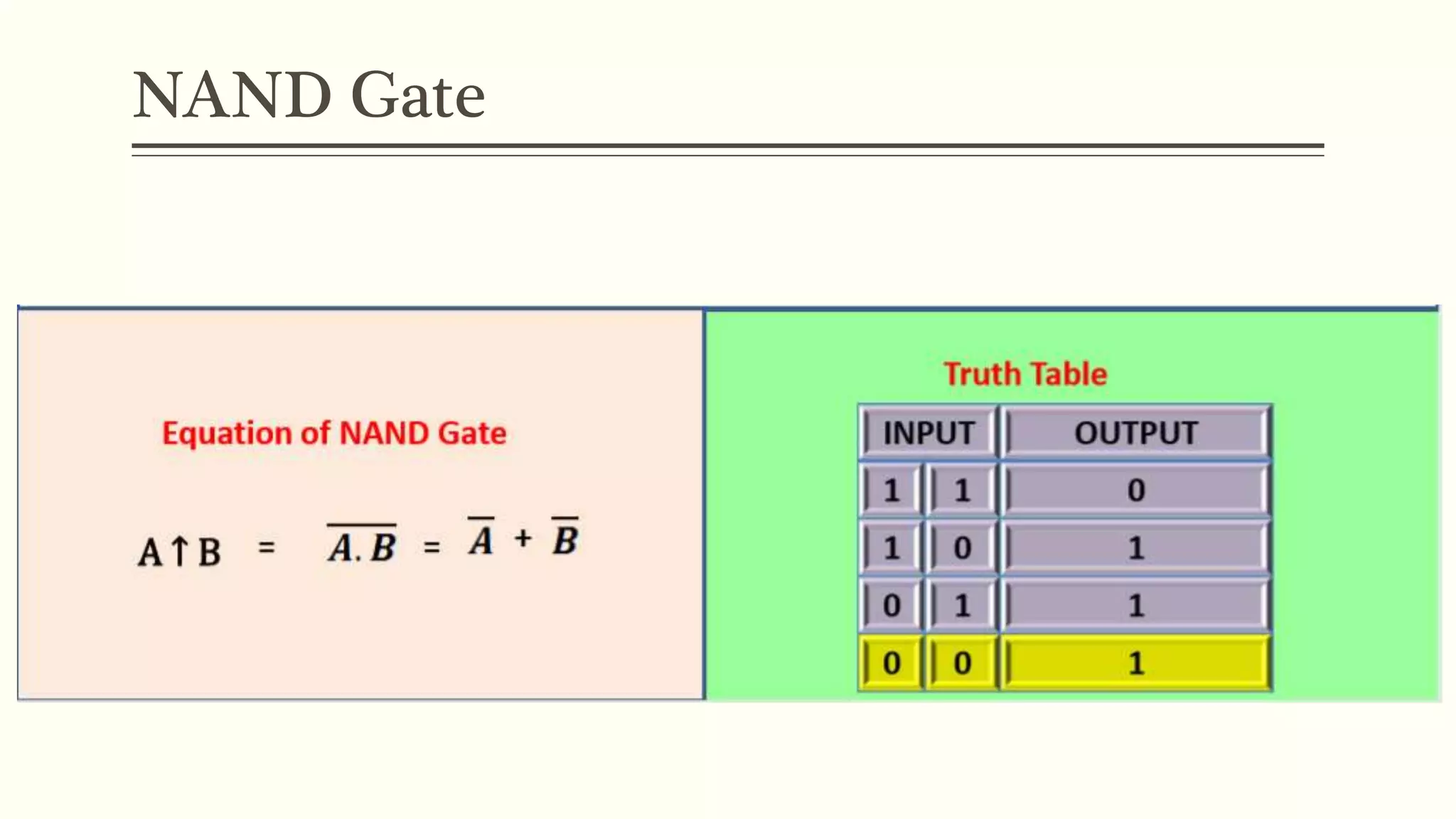
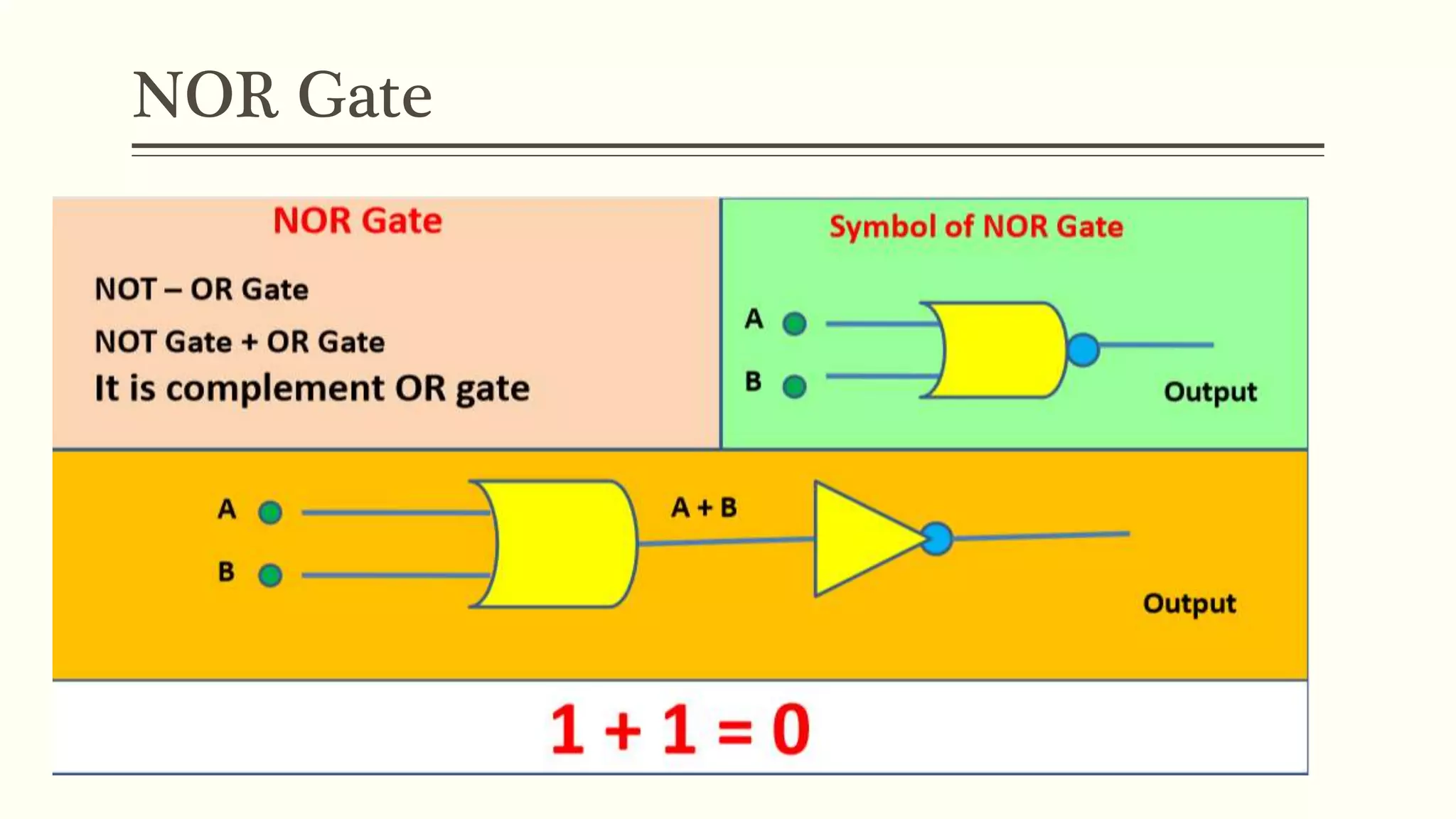
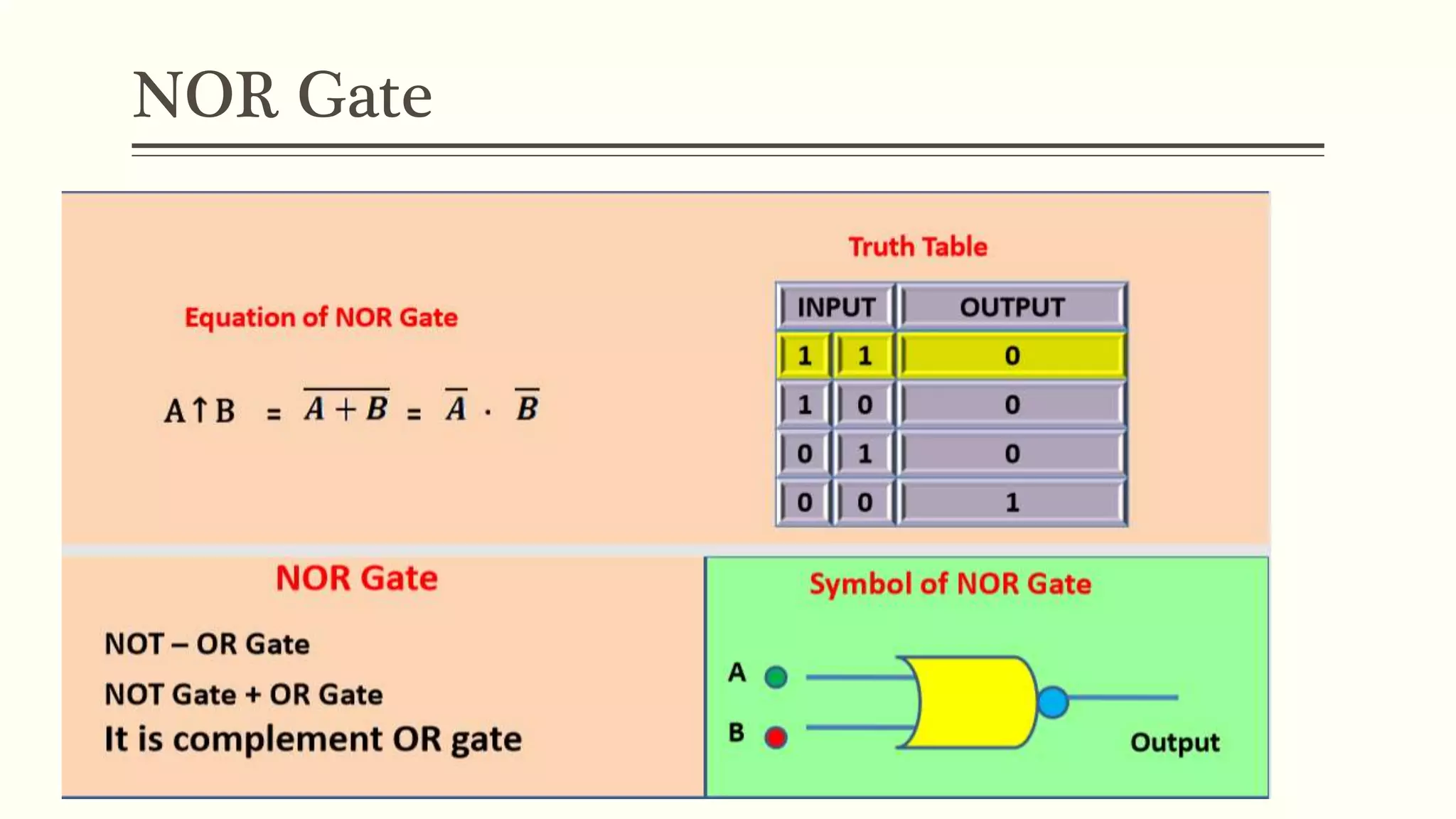
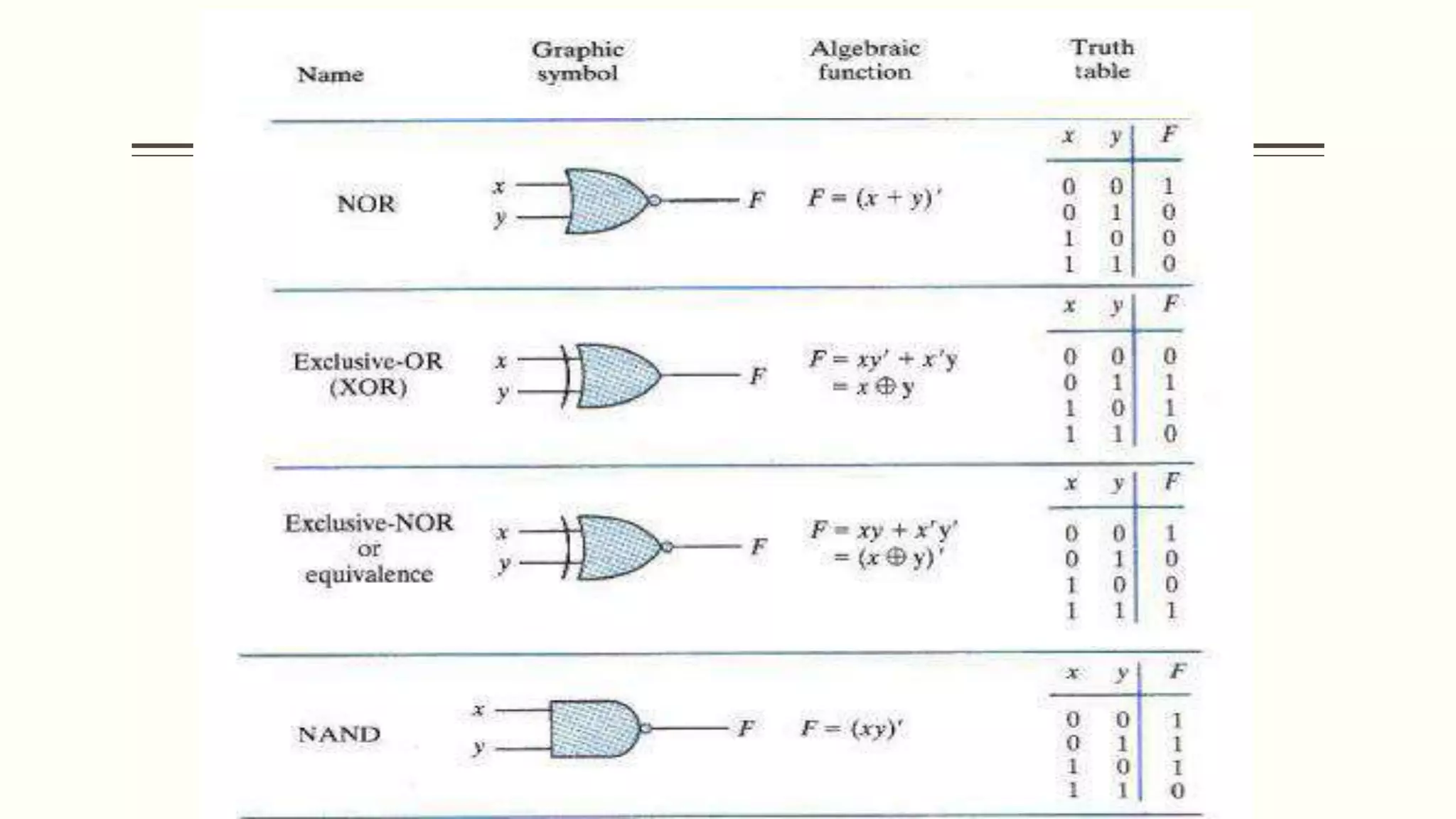
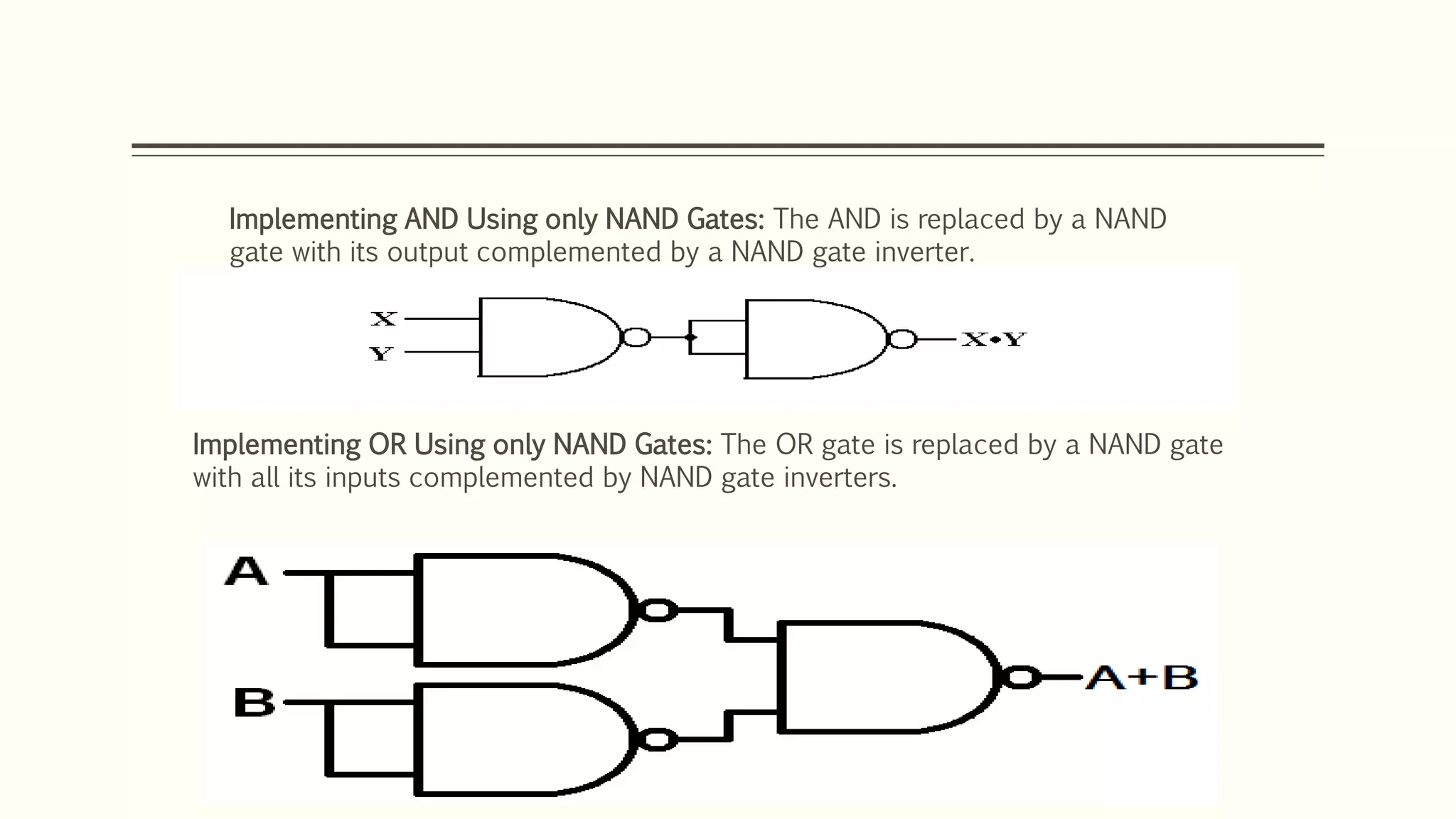
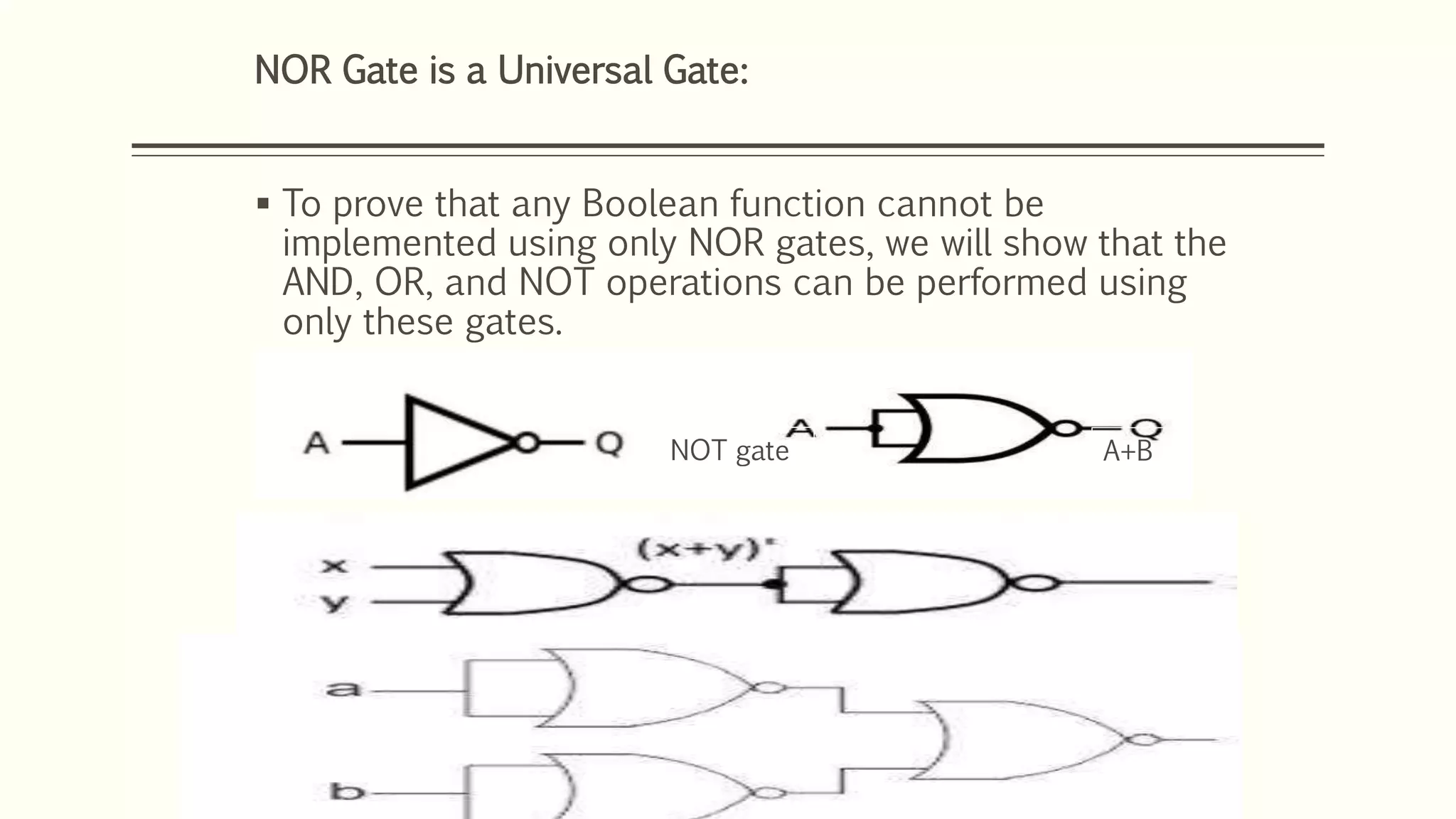
This document discusses Boolean algebra and logic gates. It defines Boolean algebra as a mathematical system using two values, typically true/false or 1/0. Boolean expressions are created using common operators like AND, OR, and NOT. Truth tables define the outputs of these operators. Logic gates are physical implementations of Boolean operators, including AND, OR, NAND, and NOR gates. Laws like De Morgan's theorem and the properties of universal gates like NAND and NOR are also covered.

1. Er. Nawaraj Bhandari
Digital Logic
Chapter 2:
Boolean algebra and Logic Gates

2. Boolean algebra
 Boolean algebra is a mathematical system for the manipulation of
variables that can have one of two values.
 In formal logic, these values are “true” and “false.”
 In digital systems, these values are “on” and “off,” 1 and 0, or “high”
and “low.”
 Boolean expressions are created by performing operations on
Boolean variables.
 Common Boolean operators include AND, OR, and NOT.

3. 3
 A Boolean operator can be
completely described using a truth
table.
 The truth table for the Boolean
operators AND and OR are shown
at the right.
 The AND operator is also known as
a Boolean product. The OR
operator is the Boolean sum.
Boolean algebra & Truth Table

4. 4
Boolean Algebra
 The truth table for the
Boolean NOT operator is
shown at the right.
 The NOT operation is most
often designated by an
overbar. It is sometimes
indicated by a prime mark ( ‘
) or an “elbow” ().
Boolean algebra

5. 5
Boolean Algebra
 A Boolean function has:
• At least one Boolean variable,
• At least one Boolean operator, and
• At least one input from the set {0,1}.
 It produces an output that is also a member of
the set {0,1}.

6. Basic Theory of Boolean Algebra
 Some basic laws for Boolean Algebra
A . 0 = 0 where A can be either 0 or 1.
A . 1 = A where A can be either 0 or 1.
A . A = A where A can be either 0 or 1.
A . Ā = 0 where A can be either 0 or 1.
A + 0 = A where A can be either 0 or 1.
A + 1 = 1 where A can be either 0 or 1.
A + Ā = 1
A + A = A
A + B = B + A where A and B can be either 0 or 1.
A . B = B . A where A and B can be either 0 or 1.

7. Duality theorem
Dual of the Boolean expression is derived by:
 Replacing AND operation by OR
 Replacing OR operation by AND
 All 1's are changed to 0
 All 0's are changed to 1
 Variables and complements are left unchanged.
 Example: X+Y'Z+0 = (0+X).(Y'+Z).1 XY'+XYZ+YZ' = (X+Y').(X+Y+Z).(Y+Z')

8. Postulates
(1) A + 0 = A A · 1 = A identity
(2) A + NOT[A] = 1 A · NOT[A] = 0 complement
(3) A + B = B + A A · B = B · A commutative law
(4)
A + (B + C) = (A + B) +
C
A · (B · C) = (A · B) · C associative law
(5)
A + (B · C) = (A + B) · (A
+ C)
A · (B + C) = (A · B) + (A
· C)
distributive law

9. De Morgan's theorem
 First Theorem:
 The De-Morgan's first theorem states that, "The complement of a sum
equals to the product of the complements".
 i.e. (A+B)'=A'.B’

10. De Morgan's theorem

11. De Morgan's theorem
Second Theorem:
De Morgan's second theorem states that, "The complement of a product is
equal to the sum of the complements."
i.e. (A.B)'=A'+B'

12. De Morgan's theorem

13. Introduction to Logic Gates
AND Gate
It is an electronic circuit, which generates an output signal of 1 if and only
if all input signals are also 1
An AND gate is the physical realization of the logical multiplication ( AND
operation

14. AND Gate

15. AND Gate

16. AND Gate

17. AND Gate

18. OR Gate
 It is an electronic circuit, which generates an output signal of 1, if any
of the output signals is 1
 It is the physical realization of logical OR

19. OR Gate

20. OR Gate

21. OR Gate

22. OR Gate

23. NOT Gate
 It is an electronic circuit that generates an output signal, which is
reverse of input signal
 It is the physical realization of complementation operation
 Not Gate is also called inverter because it inverts the input

24. NOT Gate

25. NOT Gate

26. NAND Gate
 Not AND Gate - NOT + AND gate It is a combination of NOT and AND
gates It is Complemented AND Gate
 Symbol of NAND gate

27. NAND Gate

28. NAND Gate

29. NOR Gate

30. NOR Gate

32. Universal gates
 A universal gate is a gate which can implement any Boolean function without
need to use any other gate type.
 The NAND and NOR gates are universal gates. In practice, this is
advantageous since NAND and NOR gates are economical and easier to
fabricate and are the basic gates used in all.
 NAND Gate is a Universal Gate :-To prove that any Boolean function can be
implemented using only NAND gates, we will show that the AND, OR, and
NOT operations can be performed using only these gates.
 Implementing an Inverter Using only NAND Gate: All NAND input pins
connected to the input signal A gives an output A’.

33. Implementing AND Using only NAND Gates: The AND is replaced by a NAND
gate with its output complemented by a NAND gate inverter.
Implementing OR Using only NAND Gates: The OR gate is replaced by a NAND gate
with all its inputs complemented by NAND gate inverters.

34. NOR Gate is a Universal Gate:
 To prove that any Boolean function cannot be
implemented using only NOR gates, we will show that the
AND, OR, and NOT operations can be performed using
only these gates.
NOT gate A+B

35. Complement of a function
 The complement of a function F is F' and is obtained from an interchange of 0's for 1's and
1's for 0's in the value of F.
 Two ways of getting complement of a Boolean function:
 1. Applying De-Morgan’s theorem as many times as necessary
 For example: -
 Find the complement of the function F1 and F2.
 The complement of F1 is F1’ where F1=(x'yz' + x'y'z) so
 F1 ‘=(x'yz' + x'y'z)’
 = (x'yz')'(x'y'z)'
 = (x + y' + z)(x + y + z')
 F2' = [x(y'z' + yz)]'
 = x' + (y'z' + yz)'
 = x' + (y'z')'· (yz)'
 = x' + (y + z)(y' + z')

36. ANY QUESTIONS?