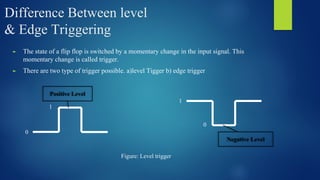
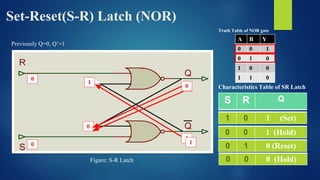
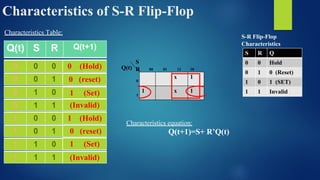
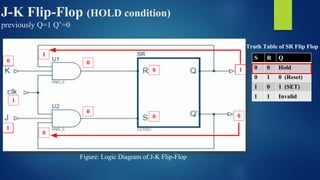
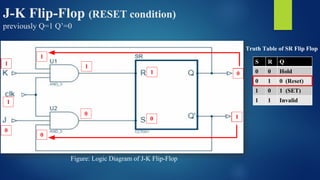
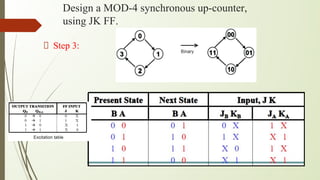
The document provides an extensive overview of sequential circuits, specifically focusing on various types of latches and flip-flops such as SR latches, JK flip-flops, D flip-flops, and T flip-flops, explaining their triggering methods, characteristics, and truth tables. It distinguishes between asynchronous and synchronous circuits, detailing how to design counters using JK flip-flops and the behavior of outputs in response to clock signals. Additionally, it includes illustration diagrams and characteristic equations for better understanding of these components and their functionalities.

1. Sequential Circuit
Latches and Flip-Flops

2. Contents
► Sequential circuit
► Triggering of sequential circuit
► SR latch
► Gated SR latch
► J-K flip-flop
► D flip-flop
► T flip-flop
► Preset Clear JK flip-flop

3. Sequential Circuit
► Output depends on present input and past history of the system
► Temporary storage device and it has two stable state.
► Two type of sequential circuit :
a) Asynchronous : Output changes any time
b) Synchronous : Output changes with clock
► Level sensitive (Latch)
► Edge triggered (Flip-Flop)
Combinational
Circuit
Memory
Inputs Outputs
clock
Figure: Block diagram of a sequential circuit

4. Difference Between level
& Edge Triggering
► The state of a flip flop is switched by a momentary change in the input signal. This
momentary change is called trigger.
► There are two type of trigger possible. a)level Tigger b) edge trigger
0
1
0
1
Positive Level
Negative Level
Figure: Level trigger

5. ► Two type of edge trigger.
a) positive edge
b) negative edge
► Positive edge means 0 to 1 transition
► Negative edge means 1 to 0 transition
► Can implement edge trigger by using capacitive coupling (RC circuit is inserted in clock) and
Master Slave flip-flop
Edge Triggering of Flip-Flops
0
1
Positive
Edge
Negative
Edge
0
1
Figure: Edge trigger
Negative
Edge
Positive
Edge

6. Observation of NOR Gate
A B Y
0 0 1
0 1 0
1 0 0
1 1 0
A
B
Y
Whenever an input is ‘1’ the output Y is ‘0’
Figure: NOR GATE
Truth Table of NOR Gate

7. Set-Reset(S-R) Latch (NOR)
S R Q
1 0 1(set)
Characteristics Table of SR Latch
Figure: S-R Latch
Let S=1, R=0
1
A B Y
0 0 1
0 1 0
1 0 0
1 1 0
Truth Table of NOR gate
0
0
0
1
1

8. Set-Reset(S-R) Latch (NOR)
S R Q
1 0 1(set)
Characteristics Table of SR Latch
Figure: S-R Latch
Previously Q=1, Q’=0
0
A B Y
0 0 1
0 1 0
1 0 0
1 1 0
Truth Table of NOR gate
0
0
0
1
1
0 0 1(hold)
0
1

9. Set-Reset(S-R) Latch (NOR)
S R Q
1 0 1(set)
Characteristics Table of SR Latch
Figure: S-R Latch
Previously Q=1, Q’=0
1
A B Y
0 0 1
0 1 0
1 0 0
1 1 0
Truth Table of NOR gate
0
0
0
1
1
0 0 1(hold)
0
0
0 1 0(reset)
1

10. Set-Reset(S-R) Latch (NOR)
S R Q
1 0 1 (Set)
Characteristics Table of SR Latch
Figure: S-R Latch
Previously Q=0, Q’=1
0
A B Y
0 0 1
0 1 0
1 0 0
1 1 0
Truth Table of NOR gate
1
1
0
0
0
0 0 1 (Hold)
0 1 0 (Reset)
0 0 0 (Hold)
0
1

11. Set-Reset(S-R) Latch (NOR)
S R Q
1 0 1 (Set)
Characteristics Table of SR Latch
Figure: S-R Latch
Previously Q=0, Q’=1
1
A B Y
0 0 1
0 1 0
1 0 0
1 1 0
Truth Table of NOR gate
1
1
1
0
0
0 0 1 (Hold)
0 1 0 (Reset)
0 0 0 (Hold)
1 1 Invalid
0
0 0

12. Set-Reset(S-R) Latch (NOR)
S R Q
1 0 1 (Set)
Characteristics Table of SR Latch
0 0 (Hold)
0 1 0 (Reset)
1 1 Invalid
Block diagram of SR Latch
Q
R
S
time
time
time
Timing diagram of a SR LATCH

13. Gated Set-Reset(S-R) Latch (NOR)
0
0
0
E S R Q
0 1 0 (Hold)
0 0 0 (Hold)
0 0 1 (Hold)
0 1 1 (Hold)
1
R
S
E S R Q
1 1 0 (SET)
1 0 0 (Hold)
1 0 1 (RESET)
1 1 1 (INVALID)
A B Y
0 0 0
0 1 0
1 0 0
1 1 1
Truth Table of AND gate
Characteristics Table
Gated S-R Latch

14. Characteristics of S-R Flip-Flop
Q(t) S R Q(t+1)
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
0 (Hold)
0 (reset)
1 (Set)
(Invalid)
1 (Hold)
0 (reset)
1 (Set)
(Invalid)
x 1
1 x 1
Q(t)
S
R 00 01 11 10
0
1
Characteristics equation:
Q(t+1)=S+ R’Q(t)
Characteristics Table:
S R Q
0 0 Hold
0 1 0 (Reset)
1 0 1 (SET)
1 1 Invalid
S-R Flip-Flop
Characteristics

15. Characteristics Table
Gated Set-Reset(S-R) Latch (NOR)
E
Gated S-R Latch
R
S
E
Q
time
time
time
time
Timing diagram of a Gated SR LATCH

16. J-K Flip-Flop
Figure: Logic Diagram of J-K Flip-Flop
• Modified version of S-R
Flip-Flop.
• Enable is replaced with
clock.
• Invalid Condition is
removed

17. JK Flip Flop
1
0
Q
0
Q
Q
1 0
1
Q
Q
Figure: Logic Diagram of J-K Flip-Flop

18. J-K Flip-Flop (SET condition)
let Q’=1
S R Q
0 0 Hold
0 1 0 (Reset)
1 0 1 (SET)
1 1 Invalid
1
0 0
1
Q = 1
0
1
1
0
Truth Table of SR Flip Flop
Figure: Logic Diagram of J-K Flip-Flop

19. J-K Flip-Flop (HOLD condition)
previously Q=1 Q’=0
0 0
1
0
0
1
0
1
0
0
0
S R Q
0 0 Hold
0 1 0 (Reset)
1 0 1 (SET)
1 1 Invalid
1
0
1
0
Truth Table of SR Flip Flop
Figure: Logic Diagram of J-K Flip-Flop

20. J-K Flip-Flop (RESET condition)
previously Q=1 Q’=0
0
1
1
0
1
0
1
0
0
0
S R Q
0 0 Hold
0 1 0 (Reset)
1 0 1 (SET)
1 1 Invalid
1
0
1
1
0
Truth Table of SR Flip Flop
Figure: Logic Diagram of J-K Flip-Flop

21. J-K Flip-Flop (Toggle condition)
previously Q=0 Q’=1
0
1
0
1
0
1
0
1
0
1
S R Q
0 0 Hold
0 1 0 (Reset)
1 0 1 (SET)
1 1 Invalid
0
1
1
1
0
Truth Table of SR Flip Flop
Figure: Logic Diagram of J-K Flip-Flop

22. Characteristics of J-K Flip-Flop
Q(t) J K Q(t+1)
0 0 0
0 0 1
0 1 0
0 1 1
1 0 0
1 0 1
1 1 0
1 1 1
0 (Hold)
0 (reset)
1 (Set)
1 (Toggle)
1 (Hold)
0 (reset)
1 (Set)
0 (Toggle)
1 1
1 1
Q(t)
J
K 00 01 11 10
0
1
Characteristics equation:
Q(t+1)=JK+ K’Q(t)
Characteristics Table:
J K Q
0 0 Hold
0 1 0 (Reset)
1 0 1 (SET)
1 1 Toggle
JK Flip Flop Characteristics

23. J-K Flip Flop
J K Q
1 0 (Set)
Characteristics table of J-K Flip Flop
0 0 (Hold)
0 1 (Reset)
1 1 Toggle
Block diagram of J-K Flip Flop
K
J
clk
Q
time
time
time
time
Timing diagram of a Gated JK Flip-Flop

24. D Flip-Flop
J
K
D
Figure: Logic Diagram of D Flip-Flop

25. D Flip-Flop
D
K
J
Q
Q
Block diagram of D Flip Flop
J K Q
1 0 (Set)
Characteristics table
of J-K Flip-Flop
0 0 (Hold)
0 1 (Reset)
1 1 Toggle
D Q
0 0
1 1
0
1
0
1 0
1
1
1
0
0 1
0
Characteristics table of D
Flip-Flop
J-K
Flip Flop
clk
N.B. INPUT AND OUTPUT SAME SO ACTS AS A BUFFER
CIRCUIT

26. Characteristics of D Flip Flop
Q(t) D Q(t+1)
0 0
0 1
1 0
1 1
0
1
0
1
1
1
Q(t)
D
0 1
0
1
Characteristics equation:
Q(t+1)=D
Characteristics Table: D Q
0 0
1 1
D Flip Flop Characteristics

27. D Flip-Flop
D Q
0 0
1 1
Characteristics table of D Flip-Flop
D
Q
Q
Block diagram of D Flip Flop
D
Flip Flop
clk
D
clk
Q
time
time
time
Timing diagram of a Gated D Flip-Flop

28. T Flip-Flop
T
Figure: Logic Diagram of T Flip-Flop

29. T Flip-Flop
T
K
J
Q
Q
Block diagram of T Flip Flop
J K Q
1 0 (Set)
Characteristics table
of J-K Flip-Flop
0 0 (Hold)
0 1 (Reset)
1 1 Toggle
T Q
0 HOLD
1 Toggle
1
1
Toggle
Characteristics table of T
Flip-Flop
J-K
Flip Flop
clk
1
0
0
0
Hold

30. Characteristics of T Flip Flop
Q(t) T Q(t+1)
0 0
0 1
1 0
1 1
0 (HOLD)
1
(TOGGLE)
1 (HOLD)
0
(TOGGLE)
1
1
Q(t)
T
0 1
0
1
Characteristics equation:
Q(t+1) = T Q(t)’ + T’ Q(t)
Characteristics Table: T Q
0 HOLD
1 TOGGLE
D Flip Flop Characteristics

31. T Flip-Flop
T
Q
Q
Block diagram of T Flip Flop
T
Flip Flop
clk
time
time
T Q
0 HOLD
1 Toggle
Characteristics table of T
Flip-Flop

32. The
End

33. Green University of Bangladesh
Department of Electrical & Electronic Engineering
Sequential Circuit

34. Triggering of Flip-flop
Combinational
Circuit
Memory
Clock Pulse
Input Output
State
Latch/Flipflop
Control Input

35. Triggering of Flip-flop
❑ Edge Trigger
❑ Level Trigger

36. Triggering of Flip-flop
❑ Level Trigger ❑ Edge Trigger
The flip flop is triggered only during the
high-level or the low level of the clock pulse.
Positive level triggering
Negative level triggering
In edge triggering, the flip flop changes its state during
the positive edge or negative edge of the clock pulse.
Positive edge triggering
Negative edge triggering

37. Triggering of Flip-flop

38. Clocked SR Flip-flop
SR Flip flop with Clock Nand Latch

39. Clocked SR Flip-flop(cont’d)
This whole Circuit is SR Flip-Flop

40. Clocked SR Flip-flop(cont’d)
Clk S R Q Q’ State
No
Change
No
Change
Memory
0 X X
S’+ 1= 1
=R’+ 1=1
S* R*

41. Clocked SR Flip-flop(cont’d)
Clk S R Q Q’ State
No
Change
No
Change
Memory
0 X X
S’+0=S’
=R’+0=R’
S* R*
1 0 0
=1
=1
Memory

42. Clocked SR Flip-flop(cont’d)
Clk S R Q Q’ State
No
Change
No
Change
Memory
0 X X
S’+0=S’
=R’+0=R’
S* R*
1 0 0
=1
=0
Memory
1 0 1 0 1

43. Clocked SR Flip-flop(cont’d)
Clk S R Q Q’ State
No
Change
No
Change
Memory
0 X X
S’+0=S’
=R’+0=R’
S* R*
1 0 0
=0
=1
Memory
1 0 1 0 1
1 1 0 1 0

44. Clocked SR Flip-flop(cont’d)
Clk S R Q Q’ State
No
Change
No
Change
Memory
0 X X
S’+0=S’
=R’+0=R’
S* R*
1 0 0
=0
=0
Memory
1 0 1 0 1
1 1 0 1 0
1 1 1 1 1 invalid

45. Truth Table for Clocked SR Flipflop(cont’d)
Clk S R Q Q’ State
No
Change
No
Change
Memory
0 X X
1 0 0 Memory
1 0 1 0 1
1 1 0 1 0
1 1 1 1 1 invalid
❑ Circuit ❑ Truth Table

46. Truth Table for Clocked SR Flipflop(cont’d)
Clk S R Qn+1
Qn
Qn
0 X X
1 0 0
1 0 1 0
1 1 0 1
1 1 1 X
❑ Characteristic Table ❑ Truth Table
Qn S R Qn+1
0 0 0 0
0 0 1 0
0 1 0 1
0 1 1 X
1 0 0 1
1 0 1 0
1 1 0 1
1 1 1 X

47. Truth Table for Clocked SR Flipflop(cont’d)
❑ Characteristic Table ❑ Excitation Table

48. ❑ Truth Table for SR flipflop
D flip-flop

49. ❑ Truth Table for SR flipflop
D flip-flop
❑ Truth Table for D flip-flop

50. D flip-flop

51. D flip-flop

52. Synchronous Counter

53. Definition
A synchronous counter , in contrast to an
asynchronous counter , is one whose output bits
change state simultaneously, with no ripple.

54. The only way we can build such a counter circuit from J-K flip-flops
is to connect all the clock inputs together, so that each and every
flip-flop receives the exact same clock pulse at the exact same time

55. Now, the question is, what do we do with the J and K inputs? We know that we still have to
maintain the same divide-by-two frequency pattern in order to count in a binary sequence, and
that this pattern is best achieved utilizing the "toggle" mode of the flip-flop, so the fact that the
J and K inputs must both be (at times) "high" is clear. However, if we simply connect all the J
and K inputs to the positive rail of the power supply as we did in the asynchronous circuit, this
would clearly not work because all the flip-flops would toggle at the same time: with each and
every clock pulse!

56. How To Design Synchronous Counter

57. Design a MOD-4 synchronous up-counter,
using JK FF.
STEP 1: No of FF=2
STEP 2: Excitation Table

58. Design a MOD-4 synchronous up-counter,
using JK FF.
Step 3:

59. Step 4: Obtain the simplified function using K-Map
B
A
B
B
B
A
A
A

60. Step 5: Draw the circuit diagram.

61. Design a MOD-8 synchronous up-counter,
using JK FF.

62. Step2: State transition diagram & State
Table

63. Step 3: Expand the present state-next state table to form the transition
table.
Excitation Table

64. Step 4: Use Karnaugh maps to identify the present state
logic functions for each of the inputs.
QB QA
QC
QB QA
QC

65. QC
QB QA

66. Circuit Implementation

67. How To Design Synchronous Counter
that count Random number
Design a Synchronous Counter to Count 4,7,3,0 and 2 respectively using
JKFlip Flop negative trigered by showing:
i. Flip Flop Used
ii. State Transition Diagram
iii. Exitation Table / Present state, next State
iv. Karnough Map & perform Simplified Function
v. The Synchronous Counter

68. n = 3 bit = 3 Flip Flop

69. Synchronous Counter to Count 4,7,3,0 and 2 respectively

70. Step 4: Karnough Map and
Simplified Function
K Map for JA
0 0 1X 3 X 2 0
4 1 5X 7 X 6 X
BA
C
4=100
5=101
7=111
6=110
C B A
JA= C=QC

71. Step 4: Karnough Map and
Simplified Function
K Map for KA
0 X 1X 3 1 2 X
4 X 5X 7 0 6 X
BA
C
0=000
1=001
3=011
2=010
C B A
KA= C=QC

72. Step 4: Karnough Map and
Simplified Function
K Map for JB
0 1 1X 3 X 2 X
4 1 5X 7 X 6 X
BA
C
JB=1

73. Step 4: Karnough Map and
Simplified Function
K Map for KB
0 X 1X 3 1 2 1
4 X 5X 7 0 6 X
BA
C
0=000
1=001
3=011
2=010
C B A
KB= C=QC

74. Step 4: Karnough Map and
Simplified Function
K Map for Jc
0 0 1X 3 0 2 1
4 X 5X 7 X 6 X
BA
C
2=010
6=110
C B A
Jc= BA=QBQA

75. Step 4: Karnough Map and
Simplified Function
K Map for Kc
0 X 1X 3 X 2 X
4 0 5X 7 1 6 X
BA
C
2=010
3=011
7=111
6=110
C B A
Kc= B=QB

76. Circuit Implementation
C
B
A