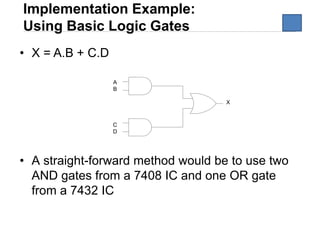
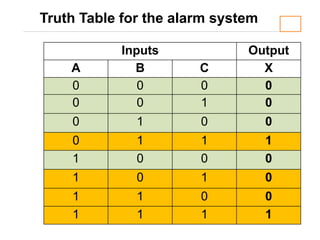
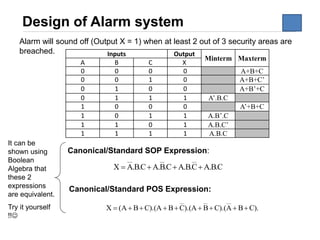
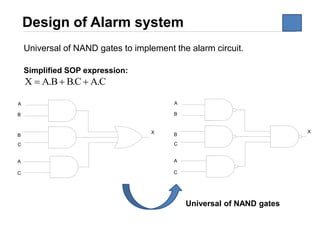
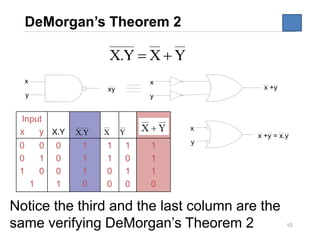
The document discusses logic circuit optimization techniques including Boolean algebra, De Morgan's theorems, and Karnaugh maps. It provides examples of simplifying logic expressions using Boolean algebra rules and theorems. Specifically, it shows how to implement the logic function for an alarm system that activates when two of three security areas are breached, using sum of products and NAND gate implementations.

1. School of Engineering
Logic circuit optimisation

2. • Further Boolean algebra, de Morgan’s
theorem
• Karnaugh maps with up to four variables
• Simplification and optimisation of circuits
using these techniques

3. 3
Simplification of Logic Circuits using
Boolean Algebra
• Need to apply the laws, rules and theorems
of Boolean Algebra to simplify Boolean
Expressions
• Simplification means fewer gates for the
same logic functions
• If equivalent logic function may be achieved
with fewer components, the result will be
increased reliability and decreased cost of
manufacture

4. 5
Rules of Boolean Algebra
AND Operator OR Operator
A.0  0 A + 0  A
A.1  A A + 1  1
A.A  A A + A  A
Note that the rules for OR operator can be obtained from AND operator
by changing the operator, and inverting the logic values (vice versa)
=> Duality of Boolean Algebra
1AA =+0A.A =

5. 8
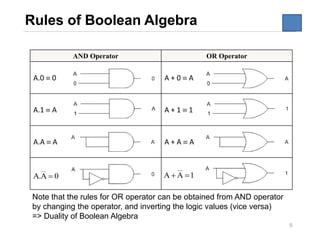
Rules of Boolean Algebra
Rule Prove ( For your information only)
The double complement of a variable is always equal to
the variable.
A + AB = A
A + AB = A (1 + B) [ Distributive Law ]
= A.1 [ Rule 2: (1 + B) = 1 ]
= A [ Rule 4: A.1 = A ]
(A + B)(A + C) = A + BC
(A + B)(A + C) = AA + AC + AB + BC [Distributive Law]
= A + AC + AB + BC [Rule 7: AA = A]
= A (1 + C) + AB + BC [Rule 2: 1 + C = 1]
= A.1 + AB + BC Factoring
= A (1 + B) + BC [Rule 2: 1 + B = 1]
= A.1 + BC [Rule 4: A.1 = A]
= A + BC

6. 9
DeMorgan’s Theorem 1
x
y
x+y
x
y
x
y
x . y = x+y
x . y
Input
x y
0 0
0 1
1 0
1 1
0
1
1
1
1
0
0
0
1
1
0
0
1
0
1
0
1
0
0
0
Notice the third and the last column are the same
verifying DeMorgan’s Theorem 1
Y.XYX =+
YX + YX + X Y Y.X

7. 10
DeMorgan’s Theorem 2
Input
x y X.Y
0 0
0 1
1 0
1
0
0
0
1
1
1
1
0
1
1
0
0
1
0
1
0
1
1
1
0
Notice the third and the last column are the
same verifying DeMorgan’s Theorem 2
x
y
xy
x
y
x
y
x +y = x.y
x +y
YXY.X +=
Y.X X Y

8. 11
Example [1] – De Morgan’s
BA+
).( ZYX +
= (A’ + B’)’
= [(A’)’.(B’)’]
= A.B
= (X.Y’ + Z)’
= (X.Y’)’.Z’
= (X’+Y).Z’
= X’.Z’ + Y.Z’

9. 12
Example [2] –De Morgan’s
ZYX ++
).).(.( CBACBA ++
= (X’+Y’)’. (Z’)’
= [(X’)’,(Y’)’]. (Z)
= [X.Y]. Z
= X.Y.Z
= (A.B’+C)’ + (A+BC)’
= (AB’)’C’ + A’(BC)’
= (A’+B)C’ + A’(B’+C’)
= A’C’ + BC’ + A’B’ + A’C’
= A’C’ + BC’ + A’B’

10. Implementation Example:
Using Basic Logic Gates
• X = A.B + C.D
A
B
C
D
X
• A straight-forward method would be to use two
AND gates from a 7408 IC and one OR gate
from a 7432 IC

11. Implementation Example:
Using only NAND gates
A
B
C
D
X
A
B
C
D
X
redundant
A
B
C
D
X
This solution only
uses three NAND
gates from one 7400
IC
=> Saves PCB area,
component costs and
power consumption!!

12. In an alarm system, the alarm will sound off
(Output X = 1) as long as security areas “B”
and “C” are breached. Inputs A, B, C
represents the 3 security areas, with logic 1
representing that the security is breached.
1) Draw the truth table for this logic function
with 3 inputs and 1 output.
2) Design the logic circuit

13. Inputs Output
A B C X
0 0 0 0
0 0 1 0
0 1 0 0
0 1 1 1
1 0 0 0
1 0 1 0
1 1 0 0
1 1 1 1
Inputs Output
A B C X
0 0 0 0
0 0 1 0
0 1 0 0
0 1 1 1
1 0 0 0
1 0 1 0
1 1 0 0
1 1 1 1
Truth Table for the alarm system

14. Design of Alarm system
Canonical/Standard SOP Expression:
Canonical/Standard POS Expression:
It can be
shown using
Boolean
Algebra that
these 2
expressions
are equivalent.
Try it yourself
!!☺
Inputs Output
Minterm Maxterm
A B C X
0 0 0 0 A+B+C
0 0 1 0 A+B+C’
0 1 0 0 A+B’+C
0 1 1 1 A’.B.C
1 0 0 0 A’+B+C
1 0 1 1 A.B’.C
1 1 0 1 A.B.C’
1 1 1 1 A.B.C
Alarm will sound off (Output X = 1) when at least 2 out of 3 security areas are
breached.
C.B.AC.B.AC.B.AC.B.AX +++=
).CBA).(CBA).(CBA).(CBA(X ++++++++=

15. Design of Alarm system
Simplified SOP expression:
Universal of NAND gates to implement the alarm circuit.
C.AC.BB.AX ++=
B
A
B
C
C
A
X
B
A
B
C
C
A
X
Universal of NAND gates