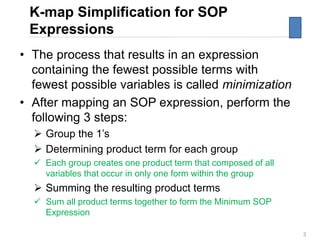
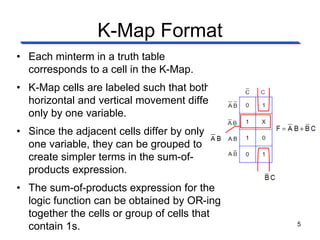
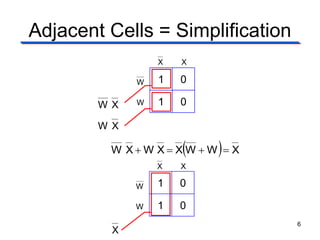
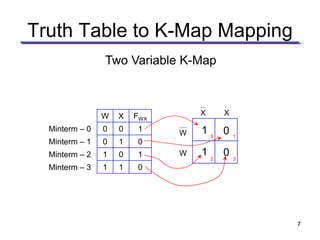
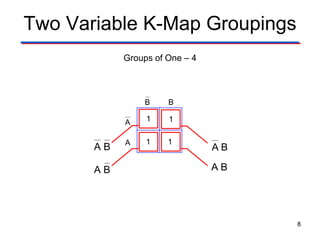
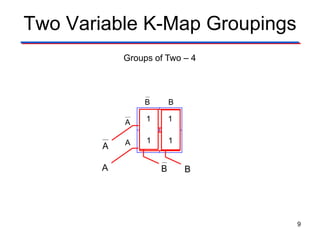
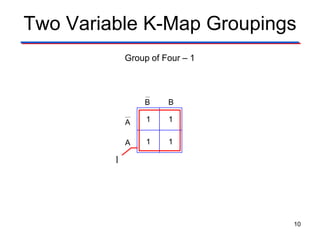
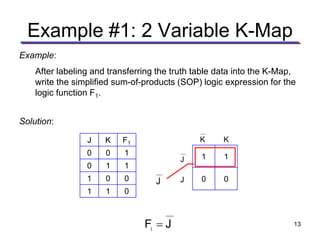
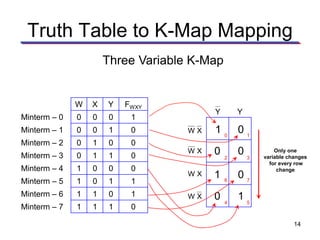
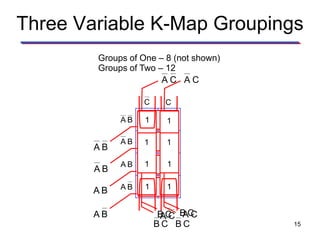
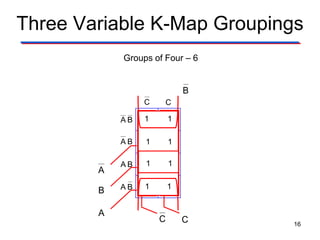
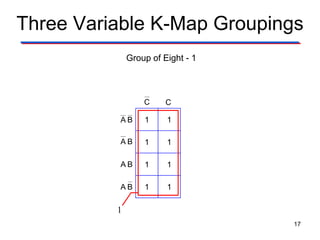
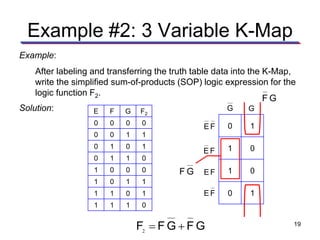
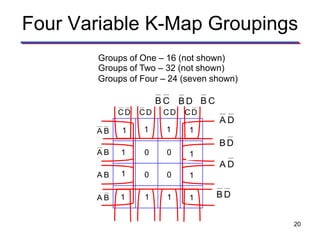
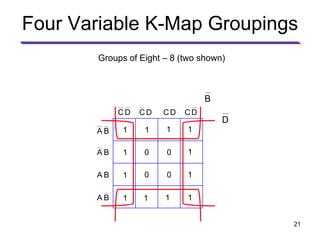
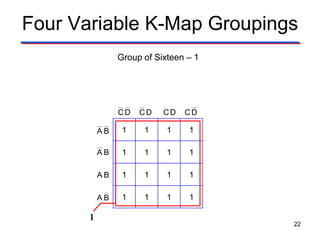
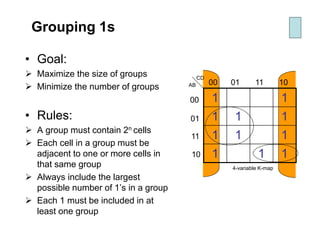
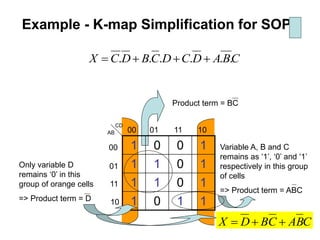
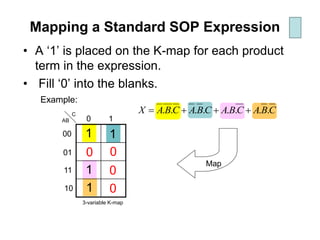
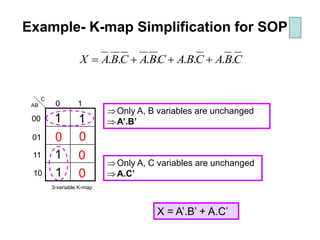
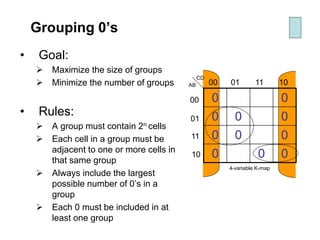
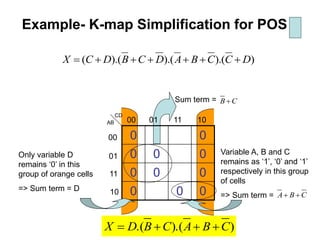
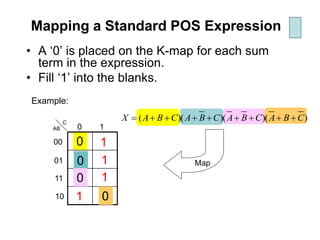
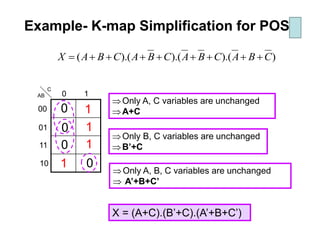
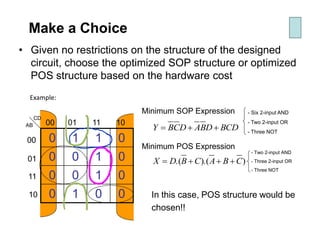
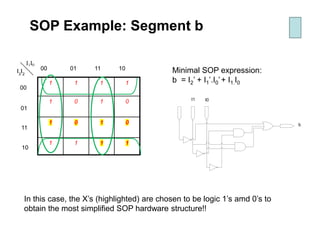
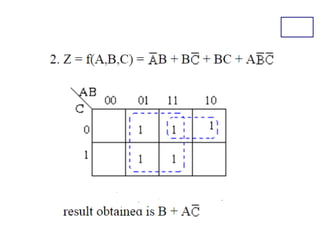
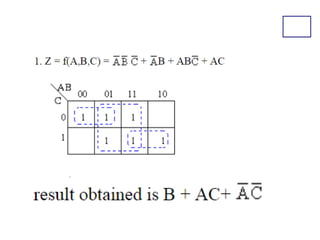
Karnaugh maps (K-maps) are used to simplify Boolean logic expressions. A K-map arranges the minterms from a truth table into an array of cells where adjacent cells differ by only one variable. Groups of adjacent 1s in the K-map correspond to terms in a sum-of-products expression. The process of mapping a logic function onto a K-map and grouping 1s results in a minimum simplified expression. Don't care conditions can be treated as 1s to form larger groups for greater simplification. Both sum-of-products and product-of-sums expressions can be mapped and minimized using K-maps.

1. Karnaugh Map

2. 2
What is K-map?
• A K-map is similar to a truth table
➢ All possible values of inputs + corresponding outputs
• A K-map is different from a truth table
➢Not rows and columns, but an array of cells
• Each cell within the K-map corresponds to a
particular combination of the input variables
➢Cells are arranged such that there is only a single-
variable change between adjacent cells, e.g. 010 cell
is adjacent to 011 cell

3. 3
K-map Simplification for SOP
Expressions
• The process that results in an expression
containing the fewest possible terms with
fewest possible variables is called minimization
• After mapping an SOP expression, perform the
following 3 steps:
➢ Group the 1’s
➢ Determining product term for each group
✓ Each group creates one product term that composed of all
variables that occur in only one form within the group
➢ Summing the resulting product terms
✓ Sum all product terms together to form the Minimum SOP
Expression

4. Karnaugh Mapping or K-Mapping
This presentation will demonstrate how to
• Create and label two, three, & four variable K-Maps.
• Use the K-Mapping technique to simplify logic designs
with two, three, and four variables.
• Use the K-Mapping technique to simplify logic design
containing don’t care conditions.
Boolean Algebra Simplification K-Mapping Simplification
≡
4

5. K-Map Format
• Each minterm in a truth table
corresponds to a cell in the K-Map.
• K-Map cells are labeled such that both
horizontal and vertical movement differ
only by one variable.
• Since the adjacent cells differ by only
one variable, they can be grouped to
create simpler terms in the sum-of-
products expression.
• The sum-of-products expression for the
logic function can be obtained by OR-ing
together the cells or group of cells that
contain 1s. 5

6. Adjacent Cells = Simplification
VV
1 0
1 0
X
W
W
X
XW
XW
X
W
W
X
X
V
1 0
1 0
( ) XWWXXWXW =+=+
6

7. Truth Table to K-Map Mapping
V
W X FWX
Minterm – 0 0 0 1
Minterm – 1 0 1 0
Minterm – 2 1 0 1
Minterm – 3 1 1 0
V
0 1
2 3
X
W
W
X
1 0
1 0
Two Variable K-Map
7

8. V
0 0
0 0
B
A
A
Groups of One – 4
Two Variable K-Map Groupings
BA
1
BA
1 1
A B
BA
1
B
8

9. V
0 0
0 0
B
A
A
Groups of Two – 4
Two Variable K-Map Groupings
B
A
1 1
A
1 1
1
B
1
1
B
1
9

10. V
1 1
1 1
B
A
A
Group of Four – 1
Two Variable K-Map Groupings
1
B
10

11. K-Map Simplification Process
1. Construct a label for the K-Map. Place 1s in cells
corresponding to the 1s in the truth table. Place 0s in the
other cells.
2. Identify and group all isolated 1’s. Isolated 1’s are ones that
cannot be grouped with any other one, or can only be
grouped with one other adjacent one.
3. Group any hex.
4. Group any octet, even if it contains some 1s already grouped
but not enclosed in a hex.
5. Group any quad, even if it contains some 1s already grouped
but not enclosed in a hex or octet.
6. Group any pair, even if it contains some 1s already grouped
but not enclosed in a hex, octet, or quad.
7. OR together all terms to generate the SOP equation. 11

12. Example #1: 2 Variable K-Map
Example:
After labeling and transferring the truth table data into the K-Map,
write the simplified sum-of-products (SOP) logic expression for the
logic function F1.
V
J K F1
0 0 1
0 1 1
1 0 0
1 1 0
12

13. Example #1: 2 Variable K-Map
Example:
After labeling and transferring the truth table data into the K-Map,
write the simplified sum-of-products (SOP) logic expression for the
logic function F1.
V
1 1
0 0
K
J
J
K
Solution:
J
JF =1
J K F1
0 0 1
0 1 1
1 0 0
1 1 0
13

14. Truth Table to K-Map Mapping
W X Y FWXY
Minterm – 0 0 0 0 1
Minterm – 1 0 0 1 0
Minterm – 2 0 1 0 0
Minterm – 3 0 1 1 0
Minterm – 4 1 0 0 0
Minterm – 5 1 0 1 1
Minterm – 6 1 1 0 1
Minterm – 7 1 1 1 0
V
0 1
2 3
6 7
4 5
Y
XW
Y
1
Three Variable K-Map
XW
XW
XW
0
0 0
0 1
1 0
Only one
variable changes
for every row
change
14

15. Three Variable K-Map Groupings
V
0 0
0 0
0 0
0 0
C C
BA
BA
BA
BA
BA
1 1
BA
1 1
BA
1 1
BA
1 1
1
CA
1
1
CA
1
1
CA
1
1
CB
1
1
CB
1
1
CA
11
CB
1
1
CB
1
Groups of One – 8 (not shown)
Groups of Two – 12
15

16. Groups of Four – 6
Three Variable K-Map Groupings
V
0 0
0 0
0 0
0 0
C C
BA
BA
BA
BA
1
C
1
1
1
1
C
1
1
1
A
1 1
1 1
B
1 1
1 1
A
1 1
1 1
B
1 1
1 1
16

17. Group of Eight - 1
Three Variable K-Map Groupings
V
1 1
1 1
1 1
1 1
C C
BA
BA
BA
BA
1
17

18. Example #2: 3 Variable K-Map
Example:
After labeling and transferring the truth table data into the K-Map,
write the simplified sum-of-products (SOP) logic expression for the
logic function F2.
E F G F2
0 0 0 0
0 0 1 1
0 1 0 1
0 1 1 0
1 0 0 0
1 0 1 1
1 1 0 1
1 1 1 0
18

19. Example #2: 3 Variable K-Map
Example:
After labeling and transferring the truth table data into the K-Map,
write the simplified sum-of-products (SOP) logic expression for the
logic function F2.
V
0 1
1 0
1 0
0 1
G G
FE
FE
FE
FE
Solution:
GFGFF +=2
GF
GF
E F G F2
0 0 0 0
0 0 1 1
0 1 0 1
0 1 1 0
1 0 0 0
1 0 1 1
1 1 0 1
1 1 1 0
19

20. Four Variable K-Map Groupings
V
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
BA
BA
BA
BA
DC DC DC DC
Groups of One – 16 (not shown)
Groups of Two – 32 (not shown)
Groups of Four – 24 (seven shown)
CB
1 1
1 1
DB
1 1
1 1
DA
1
1
1
1
CB
1 1
1 1
DB
1
1
1
1
DA
1
1
1
1 DB11
11
20

21. Four Variable K-Map Groupings
V
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
BA
BA
BA
BA
DC DC DC DC
Groups of Eight – 8 (two shown)
B
1 1 1 1
1 1 1 1
D
1
1
1
1
1
1
1
1
21

22. Four Variable K-Map Groupings
V
1 1 1 1
1 1 1 1
1 1 1 1
1 1 1 1
BA
BA
BA
BA
DC DC DC DC
Group of Sixteen – 1
1
22

23. Example #3: 4 Variable K-Map
Example:
After labeling and transferring the truth table data into the K-Map, write the
simplified sum-of-products (SOP) logic expression for the logic function
F3.
R S T U F3
0 0 0 0 0
0 0 0 1 1
0 0 1 0 0
0 0 1 1 1
0 1 0 0 0
0 1 0 1 1
0 1 1 0 1
0 1 1 1 1
1 0 0 0 0
1 0 0 1 1
1 0 1 0 0
1 0 1 1 0
1 1 0 0 1
1 1 0 1 0
1 1 1 0 1
1 1 1 1 1
V
23

24. Don’t Care Conditions
• A don’t care condition, marked by (X) in the truth
table, indicates a condition where the design
doesn’t care if the output is a (0) or a (1).
• A don’t care condition can be treated as a (0) or
a (1) in a K-Map.
• Treating a don’t care as a (0) means that you do
not need to group it.
• Treating a don’t care as a (1) allows you to make
a grouping larger, resulting in a simpler term in
the SOP equation.
24

25. Some You Group, Some You Don’t
V
X 0
1 0
0 0
X 0
C C
BA
BA
BA
BA
CA
This don’t care condition was treated as a (1).
This allowed the grouping of a single one to
become a grouping of two, resulting in a simpler
term.
There was no advantage in treating this
don’t care condition as a (1), thus it was
treated as a (0) and not grouped.
25

26. Example #4: Don’t Care Conditions
Example:
After labeling and transferring the truth table data into the K-Map, write the
simplified sum-of-products (SOP) logic expression for the logic function
F4. Be sure to take advantage of the don’t care conditions.
R S T U F4
0 0 0 0 X
0 0 0 1 0
0 0 1 0 1
0 0 1 1 X
0 1 0 0 0
0 1 0 1 X
0 1 1 0 X
0 1 1 1 1
1 0 0 0 1
1 0 0 1 1
1 0 1 0 1
1 0 1 1 X
1 1 0 0 X
1 1 0 1 0
1 1 1 0 0
1 1 1 1 0
V
26

27. Grouping 1s
• Goal:
➢ Maximize the size of groups
➢ Minimize the number of groups
• Rules:
➢ A group must contain 2n cells
➢ Each cell in a group must be
adjacent to one or more cells in
that same group
➢ Always include the largest
possible number of 1’s in a group
➢ Each 1 must be included in at
least one group
1 1
1 1 1
1 1 1
1 1 1
00
01
11
10
00 01 11 10
4-variable K-map
AB
CD

28. Grouping 1s
• Goal:
➢ Maximize the size of groups
➢ Minimize the number of groups
• Rules:
➢ A group must contain 2n cells
➢ Each cell in a group must be
adjacent to one or more cells in
that same group
➢ Always include the largest
possible number of 1’s in a group
➢ Each 1 must be included in at
least one group
1 1
1 1 1
1 1 1
1 1 1
00
01
11
10
00 01 11 10
4-variable K-map
AB
CD

29. Example - K-map Simplification for SOP
1 0 0 1
1 1 0 1
1 1 0 1
1 0 1 1
00
01
11
10
00 01 11 10AB
CD
Only variable D
remains ‘0’ in this
group of orange cells
=> Product term = D
Variable A, B and C
remains as ‘1’, ‘0’ and ‘1’
respectively in this group
of cells
=> Product term = ABC
Product term = BC
CBACBDX ++=
CBADCDCBDCX ...... +++=

30. 1
1
11
Mapping a Standard SOP Expression
• A ‘1’ is placed on the K-map for each product
term in the expression.
• Fill ‘0’ into the blanks.
CBACBACBACBAX ........ +++=
Example:
Map
00
01
11
10
0 1
3-variable K-map
AB
C
00
0
0

31. 1
1
11
Example- K-map Simplification for SOP
CBACBACBACBAX ........ +++=
00
01
11
10
0 1
3-variable K-map
AB
C
00
0
0
Only A, B variables are unchanged
A’.B’
Only A, C variables are unchanged
A.C’
X = A’.B’ + A.C’

32. K-map Simplification for POS
Expressions
• After mapping an POS expression, perform
the following 3 steps:
➢ Group the 0’s
➢ Determining sum term for each group
✓ Each group creates one sum term that composed of all
variables that occur in only one form within the group
➢ Multiplying the resulting sum terms
✓ Multiply all sum terms together to form the Minimum POS
Expression

33. Grouping 0’s
• Goal:
➢ Maximize the size of groups
➢ Minimize the number of groups
• Rules:
➢ A group must contain 2n cells
➢ Each cell in a group must be
adjacent to one or more cells in
that same group
➢ Always include the largest
possible number of 0’s in a
group
➢ Each 0 must be included in at
least one group
0 0
0 0 0
0 0 0
0 0 0
00
01
11
10
00 01 11 10
4-variable K-map
AB
CD

34. 0 0
0 0 0
0 0 0
0 0 0
00
01
11
10
00 01 11 10AB
CD
Only variable D
remains ‘0’ in this
group of orange cells
=> Sum term = D
Sum term = CB +
Variable A, B and C
remains as ‘1’, ‘0’ and ‘1’
respectively in this group
of cells
=> Sum term = CBA ++
)).(.( CBACBDX +++=
)).().().(( DCCBADCBDCX ++++++=
Example- K-map Simplification for POS

35. 0
0
Mapping a Standard POS Expression
• A ‘0’ is placed on the K-map for each sum
term in the expression.
• Fill ‘1’ into the blanks.
))()()(( CBACBACBACBAX ++++++++=
Example:
Map
00
01
11
10
0 1AB
C
0
0
1
1
1
1

36. 0
0
Example- K-map Simplification for POS
)).().().(( CBACBACBACBAX ++++++++=
00
01
11
10
0 1AB
C
0
0
1
1
1
1
Only A, C variables are unchanged
A+C
Only B, C variables are unchanged
B’+C
X = (A+C).(B’+C).(A’+B+C’)
Only A, B, C variables are unchanged
 A’+B+C’

37. Make a Choice
• Given no restrictions on the structure of the designed
circuit, choose the optimized SOP structure or optimized
POS structure based on the hardware cost
0 1 1 0
0 0 1 0
0 0 1 0
0 1 0 0
00
01
11
10
00 01 11 10AB
CD
BCDDBADCBY ++=
Minimum SOP Expression
Minimum POS Expression
)).(.( CBACBDX +++=
- Six 2-input AND
- Two 2-input OR
- Three NOT
- Two 2-input AND
- Three 2-input OR
- Three NOT
In this case, POS structure would be
chosen!!
Example:

38. SOP Example: Segment b
Minimal SOP expression:
b = I2’ + I1’.I0’+ I1.I0
In this case, the X’s (highlighted) are chosen to be logic 1’s amd 0’s to
obtain the most simplified SOP hardware structure!!
1 1 1 1
1 0 1 0
1 0 1 0
1 1 1 1
I3
I2
I1I0
00
01
11
10
00 01 11 10
I0I1
b

42. • K-map basics
• http://www.ee.surrey.ac.uk/Projects/Labview/
minimisation/karnaugh.html
• http://www.allaboutcircuits.com/vol_4/chpt_8
/5.html
• K-map SOP/POS demonstration
• http://www.youtube.com/watch?v=5UUOTHq
bXpE
• http://www.youtube.com/watch?v=d8OxGyaq
QPM