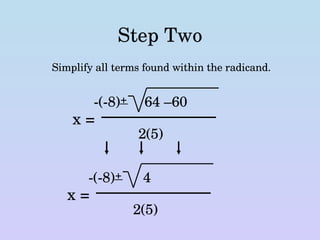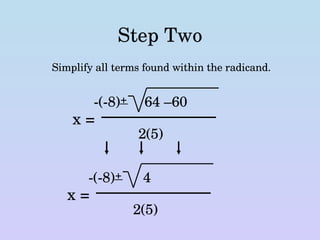
This document summarizes the steps to solve a quadratic equation using the quadratic formula. It works through solving the specific equation 5y^2 - 8y + 3 = 0 as an example. The key steps are: 1) Identifying the coefficients a, b, and c; 2) Plugging these into the quadratic formula; 3) Simplifying the terms; 4) Isolating the variable to find the solutions of 1 and 0.6. These solutions are then checked by substituting them back into the original equation.

1. Quadratic Equations (Quadratic Formula) by Rich Rollo

2. The Equation 5y 2 –8y + 3 = 0

3. The Quadratic Formula x = -b + b 2 –4ac 2a

4. Identify the Parts ay 2 + by + c = 0 5y 2 –8y + 3 = 0 Therefore in this case, a = 5, b = -8, and c = 3.

5. Step One Plug in the values of a, b, and c into the quadratic formula. x = -(-8) + (-8) 2 –4(5)(3) 2(5)

6. Step Two Simplify all terms found within the radicand. x = -(-8) + 64 –60 2(5) x = -(-8) + 4 2(5)

7. Step 3 Simplify the remaining terms in the formula. x = -(-8) + 4 2(5) x = 8 + 2 10

8. Step 4 Isolate the variable to find the solution set. x = 8 + 2 10 X = 8 + 2 X = 8 –2 10 10 = = 1 .6 &

9. Solution Set 1 and .6

10. Check the 1 st Solution Check ………………………………………… 1 5y 2 –8y + 3 = 0 5(1) 2 –8(1) + 3 = 0 5 –8 + 3 = 0 True

11. Check the 2 nd Solution Check ………………………………six-tenths. (.6) 5y 2 –8y + 3 = 0 5(.6) 2 –8(.6) + 3 = 0 1.8 –4.8 + 3 = 0 True

12. Therefore 1 and .6 is the solution set for 5y 2 –8y + 3 = 0