This document provides information about a mathematics exam paper that will take place on April 10, 2014 and has a moderate to tough difficulty level. The paper will consist of 60 multiple choice questions (MCQ) and short answer type questions (SCQ) across various topics in fundamentals of mathematics including quadratic equations. The questions are divided into 10 sets with varying number of MCQ and SCQ in each set. The total marks for the paper are 210.

1. -1
MATHEMATICS PAPER : CT-1
TARGET DATE : 10-04-2014
PAPER LEVEL : MODERATE TO TOUGH
SYLLABUS : Fundamentals of Mathematics-I, Quadratic Equation
S.No. Subject Nature of Questions No. of Questions Marks Negative Total
1 to 10 SCQ 10 3 –1 30
11 to 15 MCQ 5 4 0 20
16 to 20 Integer (double digits) 5 4 0 20
21 to 30 SCQ 10 3 –1 30
31 to 35 MCQ 5 4 0 20
36 to 40 Integer (double digits) 5 4 0 20
41 to 50 SCQ 10 3 –1 30
51 to 55 MCQ 5 4 0 20
56 to 60 Integer (double digits) 5 4 0 20
60 210
Paper-1 CT-1
Total Total
Maths
Physics
Chemistry
SCQ
1. Let n be an integer greater than 1 and let an =
n
1
log 1001
. If b = a3 + a4 + a5 + a6 and [BALG]
c = a11 + a12 + a13 + a14 + a15. Then value of (b – c) is equal to
ekukn, 1 lscM+hiw.kkZad la[;kgSrFkkekukan =
n
1
log 1001
;fn b = a3 + a4 + a5 + a6 vkSj c = a11 + a12 + a13 +
a14 + a15 rc (b – c) dkeku cjkcj gS-
(A) 1001 (B) 1002 (C) – 2 (D*) –1
Sol. an = log1001n
b = log10013 × 4 × 5 × 6 and c = log1001(11×12×13×14×15)
 (b – c) = log1001
3 4 5 6
11 12 13 14 15
   
     
= log1001(1001)
–1
= –1
2. The number of integral values of 'a' for which both roots of the equation x
2
– 2x – a
2
= 0 lie between the
roots of equation x
2
– 2x + a
2
–11a + 12 = 0, is [QELR]
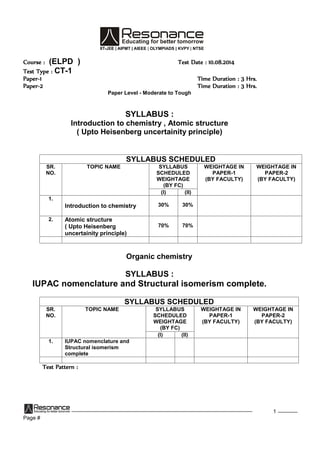
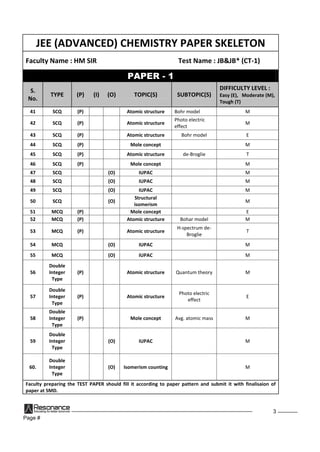
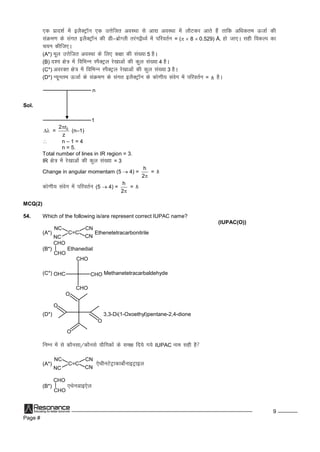
'a' dsiw.kkZad ekuksadhla[;kftldsfy, lehdj.kx
2
– 2x – a
2
= 0 dsnksuksaewy lehdj.kx
2
– 2x + a
2
–11a + 12 = 0 es
ewyksadse/; fLFkr gS-
(A) 0 (B) 1 (C*) 2 (D) 3
Sol. Let  be the root of x
2
– 2x – a
2
= 0
ekuk lehdj.kx
2
– 2x – a
2
= 0 dsewy gS
 
2
– 2 = a
2
and roots of x
2
– 2x – a
2
= 0 lie between roots of x
2
– 2x + a
2
– 11a + 12 = 0
rFkkx
2
– 2x – a
2
= 0 ds ewy lehdj.kx
2
– 2x + a
2
– 11a + 12 = 0 dsewyksdse/; fLFkr gS
 
2
– 2 + a
2
– 11a + 12 < 0  
2
– 2 = a
2
 a
2
+ a
2
– 11a + 12 < 0
 2a
2
– 11a + 12 < 0
 (2a – 3)(a – 4) < 0
 a 
3
, 4
2
 
 
 
 number of integral values of 'a' is = 2
 'a' dsiw.kkZad ekuksadhla[;k= 2 gS

2. -2
3. If x = 2 + 3i, then value of x
4
– x
3
+ 10x
2
+ 3x – 5 is equal to [BAGQ]
;fn x = 2 + 3i rc x
4
– x
3
+ 10x
2
+ 3x – 5 dkeku cjkcj gS-
(A) 127 (B) 122 (C) 120 (D*) – 122
Sol.  x = 2 + 3i
 (x – 2)
2
= – 9  x
2
– 4x + 13 = 0
 x
4
– x
3
+ 10x
2
+ 3x – 5 = (x
2
– 4x + 13)(x
2
+ 3x + 9) – 122
= – 122
4. The complete solution set of inequation
x 2
2
(e – 2)(x – 5x 4)
(x – 5x 6)


 0, is [BAIR]
vlfedk
x 2
2
(e – 2)(x – 5x 4)
(x – 5x 6)


 0 dklEiw.kZgy leqPp; gS&
(A) (–, –1] [n 2,2)  (3, 4] (B) (–,n 2] (1, 2)  (3, 4]
(C*) (–,n 2] [1, 2)  (3, 4] (D) [n 2, 1] (2, 3)  [4, )
Sol.
x
(e – 2)(x – 1)(x – 4)
(x – 2)(x – 3)
 0
x  (–,n 2] [1, 2)  (3, 4]
5. Product of the roots of the equation 2
2
1
2 x
x
 
 
 
– 9
1
x
x
 
 
 
+ 14 = 0, is
lehdj.k 2
2
1
2 x
x
 
 
 
– 9
1
x
x
 
 
 
+ 14 = 0 dsewyksadkxq.kuQy gS-
(A) 5 (B) 2 (C) 10 (D*) 1
Sol. Given equation become nhxbZlehdj.k
2x
4
– 9x
3
+ 14x
2
– 9x + 2 = 0
 product of roots ewyksadkxq.kuQy = 1
Alter
Let ekukx +
1
x
= t
  2
2 t – 2 – 9t + 14 = 0 2t
2
– 9t + 10 = 0
t = 2,
5
2
 x +
1
x
= 2 or x +
1
x
=
5
2
x = 1, x = 1 or x = 2,
1
2
 product of roots = 1
ewyksadkxq.kuQy = 1
6. The number of integral values of x satisfying
2 2
x x x x 1
4 3.2 4 
  is [QEMS]
2 2
x x x x 1
4 3.2 4 
  dkslarq"V djusokysx dsiw.kkZad ekuksadhla[;kgS-
(A) 5 (B) 3 (C*) 4 (D) 2
Sol. 
2 2
x x x x 1
4 3.2 4 
 

2 2
x x x x 1
4 – 3.2 – 4 0 


2 2
2x x x 2x 2
2 – 3.2 – 2 0 


2 2 2
2x x x x x 2x 2
2 – 4.2 2 – 2 0  
 

2 2 2
x x x x x x 2
2 (2 – 4.2 ) 2 (2 – 2 ) 0
 

3. -3

2 2
x x x x
(2 – 4.2 )(2 2 ) 0 

2
x x
(2 – 4.2 ) 0

2
x x
2 4.2
x
2
 x + 2 x
2
– x – 2  0
(x – 2)(x + 1)  0 x  [–1, 2] 4 integers iw.kk±d
7. Complete set of real values of k for which kx – x
2
+ 9 – x < 0  x  R is [QEGR]
(A) (0, ) (B) k  (–, ) (C) k  (–, –1] (D*) no such real k exists
k dsokLrfod ekuksadklEiw.kZleqPp; ftldsfy, kx – x
2
+ 9 – x < 0  x  R gS-
(A) (0, ) (B) k  (–, )
(C) k  (–, –1] (D*) k dkdksbZokLrfod eku fo|eku ugh
Sol. Roots are real as product of roots negative
ewy okLrfod gSrFkkewyksadkxq.ku_ .kkRed gSA
Alter
– x
2
+ x(k – 1) + 9 < 0
D < 0
(k – 1)
2
– 4 × (–1)(+9) < 0
(k – 1)
2
+ 36 < 0
No real k exists
k dkdksbZokLrfod eku fo|eku ugha
8. If the equation (a
2
+ a – 30)x
2
+ (b – 1)(a
2
–2a – 15)x + (b
2
– 6b + 5) = 0 has more than two different
solutions for x, then number of possible ordered pairs (a, b) is [QEGR]
;fn lehdj.k(a
2
+ a – 30)x
2
+ (b – 1)(a
2
–2a – 15)x + (b
2
– 6b + 5) = 0 dsx dsfy, nkslsvf/kd gy j[krsgS
rc (a, b) dslaHkkfor Øfer ;qXeksadhla[;kgS-
(A) 1 (B) 2 (C*) 3 (D) 4
Sol. for more than two different solution, the equation must be an identity and for that
nkslsvf/kd gy dsfy, lehdj.k,d loZlfedkgksxh
a
2
+ a – 30 = 0 and vkSj (b – 1)(a
2
– 2a – 15) = 0 and vkSj(b
2
– 6b + 5) = 0
a = –6, a = 5 and vkSj b = 1, a = 5, a = –3 and vkSjb = 1, b = 5
possible ordered pairs (a, b) are
lefor Øfer ;qXe (a, b) gS
(5, 1), (5, 5), (–6, 1)
 three possible ordered pairs (a, b) are there.
 rhu laHkkfor Øfer ;qXe (a, b) gS
9. If , ,  are the roots of the equation 2x
3
– 7x
2
+ 3x – 1 = 0, then the value of (1 – 
2
)(1 – 
2
)(1 – 
2
) is
;fn lehdj.k2x
3
– 7x
2
+ 3x – 1 = 0 dsewy , , gSrks(1 – 
2
)(1 – 
2
)(1 – 
2
) dkeku gS- [QETE]
(A) 39 (B) – 39 (C)
39
4
(D*) –
39
4
Sol.  2x
3
– 7x
2
+ 3x – 1 = 0 b
g
 2x
3
– 7x
2
+ 3x – 1= 2(x – )(x – )(x – ) ……..(i)
(i) put x = 1 j[kusij, we get
2(1 – )(1 – )(1 – ) = – 3 ……….(ii)
(ii) put x = – 1 in (1) esaj[kusij, we get
2(–1 – )(–1 – )(–1 – ) = –13  2(1 + )(1 + )(1 + ) = 13 ………(iii)
multiply (2) and (3), we get
4(1 – 
2
)(1 – 
2
)(1 – 
2
) = –39
10. The complete solution set of the inequation
1/ 2
1
log | x |
> 1 is [BAMS]

4. -4
vlfedk
1/ 2
1
log | x |
> 1 dklEiw.kZgy leqPp; gS-
(A)
1
–2, –
2
 
 
 

1
, 1
2
 
 
 
(1, 2) (B)
1
–2, –
2
 
 
 

1
, 2
2
 
 
 
(C*) (–2, – 1) 
1
–1, –
2
 
 
 

1
, 1
2
 
 
 
(1, 2) (D) 
Sol.
1/ 2
1
log | x |
> 1
 1/ 2log | x | < 1 but ijUrq log1/2|x|  0
 –1 < log1/2|x| < 1 but ijUrq|x|  1  x  1, – 1
 2 > |x| >
1
2

1
2
< |x| < 2
 x  (–2, – 1) 
1
–1, –
2
 
 
 

1
, 1
2
 
 
 
(1, 2)
MCQ
11. If range of expression
2
x – 12
2x – 7
(x  R) is (–, a]  [b, ) and let the solution of the equation
a alog b log x 3
a.x b b  is x = c, then [QEGR]
(A) (a + b) and c are both prime (B*) (a + b) and c are coprime number
(C*) (a + b + c) is a perfect square (D) a + b = c
;fn O;atd
2
x – 12
2x – 7
(x  R) dkifjlj(–, a]  [b, ) gSrFkklehdj.k a alog b log x 3
a.x b b  dkgy x = c gSrc -
(A) (a + b) vkSjc nksuksavHkkT; gSA (B*) (a + b) rFkkc lgvHkkT; la[;kgSA
(C*) (a + b + c) ,d iw.kZoxZgSA (D) a + b = c
Sol. Let ekuk y =
2
x – 12
2x – 7
 x
2
– 2xy + 7y – 12 = 0
 D  0
 4y
2
– 4 × 1 × (7y – 12)  0
 y
2
– 7y + 12  0
 y  (–, 3]  [4, )
 a = 3 and vkSjb = 4
 equation becomes 3 3log 4 log x
3.x 4 64 
 lehdj.k 3 3log 4 log x
3.x 4 64  ls
 3 3log x log x
3(4 ) 4 64 
 3log x
4 16  3log x = 2
 x = 9 = c
12. Let a and b are the solutions of the equation 4 1/ 41 log x –1 log x 26
5 5
5
 
  such that a > b, then the value of
a
b
is
(A*) an even number (B*) a rational number [BALG]
(C*) a composite number (D) a prime number
ekuka vkSj b lehdj.k 4 1/ 41 log x –1 log x 26
5 5
5
 
  dsgy bl izdkj gSfd a > b rc
a
b
dkeku gS–

5. -5
(A*) le la[;k (B*) ifjes; la[;k
(C*) la;qDr la[;k (D) vHkkT; la[;k
Sol. 4 4log x –log x–1 26
5.5 5 .5
5
 
Let ekuk 4log x
5 = t
 5t +
1
5t
=
26
5
 25t
2
– 26t + 1 = 0
 t = 1 or t =
1
25
 log4x = 0 or ;k log4x = – 2
 x = 1 or ;k x =
1
16

a
b
= 16
13. If ax
2
+ bx + c = 0 has imaginary roots and a,b,c  R, then which of the following options are CORRECT?
;fn ax
2
+ bx + c = 0 dsdkYifud ewy gSrFkka,b,c  R, rc fuEu esalsdkSulsfodYi lghgS? [QEGR]
(A) ax
2
+ bx + c > 0  x  R (B*) a(a – b + c) > 0
(C*) a(ax
2
+ bx + c) > 0  x  R (D*) a
2
+ c
2
+ 2ac > b
2
Sol.  D < 0
 (ax
2
+ bx + c) will be of same sign as that of 'a'
(ax
2
+ bx + c) 'a' dsleku fpUg dkgksxk
 C is correct lghgS
(B) Let ekukf(x) = ax
2
+ bx + c
 D < 0
Two graphs are possible nksvkj[kslaHko gS
–1
a > 0 and rFkkf(–1) > 0  a – b + c > 0
 a(a – b + c) > 0
–1
a < 0 and rFkk f(–1) < 0  a – b + c < 0
 a(a – b + c) > 0
(D) a
2
+ c
2
+ 2ac – b
2
> 0
(a + c)
2
– b
2
> 0
 (a – b + c)(a + b + c) > 0
f(–1) f(1) > 0 true lR; see the above two graphs nksvkjs[kmij fn[kk;svuqlkj
14. The value of
2 2
nb
a b
( na)( nb)
6a log b log a
e

 
is [BALG]
(A*) independent of a (B*) independent of b (C) dependent on a (D) dependent of b
2 2
nb
a b
( na)( nb)
6a log b log a
e

 
dkeku gS-
(A*) a lsLora=k (B*) b lsLora=k (C) a ij fuHkZj (D) b ij fuHkZj

6. -6
Sol.
2 2
nb
a b
na nb
6a log b log a
e

 
=
nb
a b
nb
1 1
6.a . log b. log a
2 2
a


=
6
4
=
3
2
15. Identify which of the following statement(s) are 'CORRECT' ? [QEGR]
(A*) For ax
2
+ bx + c = 0, (a  0) if 4a + 2b + c = 0, then roots are 2 and
c
2a
.
(B) If  is repeated root of ax
2
+ bx + c = 0, (a  0) then ax
2
+ bx + c = (x – )
2
.
(C*) For ax
2
+ bx + c = 0, (a  0, a,b,c  Q) imaginary roots occur in conjugate pair only.
(D*) If f(x) = ax
2
+ bx + c, (a  0) has finite maximum value and both roots of f(x) = 0 are of opposite sign,
then f(0) > 0.
fuEu esalsdkSulkdFku lghgS?
(A*) ax
2
+ bx + c = 0, (a  0) dsfy, ;fn 4a + 2b + c = 0 rc ewy 2 vkSj
c
2a
gSA
(B) ;fn , ax
2
+ bx + c = 0, (a  0) dkiqujko`fÙkewy gS]rc ax
2
+ bx + c = (x – )
2
.
(C*) ax
2
+ bx + c = 0, (a  0, a,b,c  Q) dsfy, dkYifud ewy dsoy la;qXehgksrsgSA
(D*) ;fn f(x) = ax
2
+ bx + c, (a  0) fu;r vf/kdre eku j[krkgSrFkkf(x) = 0 dsnksuksaewy foijhr fpUg dsfpUg gS]
rc f(0) > 0.
Sol. (A)  4a + 2b + c = 0  ax
2
+ bx + c = 0 has one root as 2
 other root will be
c
2a
(B) ax
2
+ bx + c = a(x – )
2
(C) coefficients are rational  coefficients are real.
imaginary roots occur in conjugate pair
(D)  f(0) > 0
Integer Type
16. If x  R then absolute difference between the maximum and minimum values of the expression
2
2
x 14x 9
x 2x 3
 
 
is [QEGR]
;fn x  R rc O;atd
2
2
x 14x 9
x 2x 3
 
 
dsvf/kdre vkSj U;wure ekuksadkfujis{kvUrj gS&
Ans. 09
Sol. Let ekuky =
2
2
x 14x 9
x 2x 3
 
 
x
2
(y – 1)+ 2x(y – 7) + 3(y – 3) = 0 ………….(i)
Case-1 : If y = 1, then equation (i) becomes
–12x – 6 = 0  x =
1
2
which is real tksfd okLrfod gSA
 y = 1 is possible laHko gSA
Case-2 : If y  1, then D  0
4(y – 7)
2
– 4(y – 1).3(y – 3)  0
y
2
– 14y + 49 – 3(y
2
– 4y + 3)  0
–2y
2
– 2y + 40  0
 y
2
+ y – 20  0
 –5  y  4
 Absolute difference = 9
fujis{kvUrj = 9

7. -7
17. If a,b  R, then the smallest natural number 'b' for which the equation x
2
+ 2(a + b)x + (a – b + 8) = 0 has
unequal real roots for all a  R, is [QENR]
;fn a,b  R, rc U;wure izkd`r la[;k'b' ftldsfy, lehdj.kx
2
+ 2(a + b)x + (a – b + 8) = 0 dslHkha  R ds
fy, vleku okLrfod ewy gS&
Ans. 05
Sol. D = 4(a + b)
2
– 4 × 1 × (a – b + 8)
= 4[a
2
+ 2ab + b
2
– a + b – 8]
= 4[a
2
+ a(2b – 1) + (b
2
+ b– 8)]
 for unequal real root for all a  R
lHkha  R dsfy, lHkhvleku okLrfod ewy gS
D > 0  a  R
(2b – 1)
2
– 4 × 1 × (b
2
+ b – 8) < 0
4b
2
– 4b + 1– 4b
2
– 4b + 32 < 0
– 8b + 33 < 0
8b > 33
b >
33
8
 smallest natural value of b is = 5
b dkU;wure izkd`r eku = 5
18. Let the product of all the solutions of the equation 33 3
3 x 3(log 3x log 3x)log x = 2 be k, then find the
value of 18k. [BALG]
ekuklehdj.k 33 3
3 x 3(log 3x log 3x)log x = 2 dslHkhgyksadkxq.kuQy k gSrc 18k dkeku Kkr dhft,
Ans. 02
Sol. squaring we get
oxZdjusij
1/ 3
1/ 3 3
3
3
log (3x)
log (3x)
log x
 
 
 
3log3x = 4
Let ekuklog3x = t

1
3
(t 1)(t 1)
t
 
.3t = 4
 t + 1 = ±2
 x = 3 or x =
1
27
 product of roots xq.kuQy dsewy =
1
9
= k
 18k = 2
19. If a, b and c are real numbers such that a2 + 2b = 7, b2 + 4c = –7 and c2 + 6a = –14, then find the value of
2 2 2
a b c
2
 
. [BAMS]
;fn a, b vkSj c okLrfod la[;kbl izdkj gSfd a2 + 2b = 7, b2 + 4c = –7 vkSjc2 + 6a = –14 gS]rks
2 2 2
a b c
2
 
dkeku Kkr dhft,A
Ans. 07
Sol. a2 + b2 + c2 + 6a + 4c + 2b = – 14
(a + 3)2 + (b + 1)2 + (c + 2)2 = 0
 a = – 3, b = – 1 and vkSj c = – 2
so blfy,
2 2 2
a b c
2
 
=
9 1 4
2
 
= 7

8. -8
20. Find the number of integral values of 'm' less than 50, so that the roots of the quadratic equation
mx
2
+ (2m – 1)x + (m – 2) = 0 are rational. [BAMS]
50 lsNksVsm dsiw.kk±d ekuksadhla[;kKkr dhft, tcfd f}?kkr lehdj.kmx
2
+ (2m – 1)x + (m – 2) = 0 dsewy
ifjes; gSA
Ans.06
Sol. D = 4m + 1
now for roots to be rational  must be perfect square of a rational number
but since m is an integer  it will be perfect square of an integer.
so let blfy, ekuk4m + 1 = k
2
, k 
 m =
2
k – 1
4
for m to be an integer k must be odd
 k = ±1, ±3, ±5, ±7, ±9, ±11, ±13
but ijUrqm  0  There are 6 possible integral values of m.

9. Page No.-1
JEE – ADVANCED (CT – 1)
Date : - 10/8/2014
Test Syllabus : Mathematical Tools, Rectilinear Motion, Projectile Motion & Relative Motion complete
S.No. Subject Nature of Questions No. of Questions Marks Negative Total
1 to 10 SCQ 10 3 –1 30
11 to 15 MCQ 5 4 0 20
16 to 20 Integer (double digits) 5 4 0 20
21 to 30 SCQ 10 3 –1 30
31 to 35 MCQ 5 4 0 20
36 to 40 Integer (double digits) 5 4 0 20
41 to 50 SCQ 10 3 –1 30
51 to 55 MCQ 5 4 0 20
56 to 60 Integer (double digits) 5 4 0 20
60 210
Paper-1 CT-1
Total Total
Maths
Physics
Chemistry
PAPER-1
SECTION-1 : (Only One option correct type)
[k.M–1 : (d soy ,d lghfod Yi çd kj)
This section contains 10 multiple choice questions. Each question has four choices (A), (B), (C) and
(D) out of which ONLY ONE is correct.
bl [k.M esa10 cgqfod Yi ç'u gSA çR;sd ç'u esapkj fod Yi (A), (B), (C) vkSj (D) gS] ft uesalsd soy ,d
lghgSA
SCQ_(10)
21. If the tangent on the curve 2
y kx (where k is a constant) at x = 1makes an angle 45o
with +x-axis,
then the value of k is
;fn oØ 2
y kx (;gkWk ,d fu;rkad gS) ij x = 1 ij [khaphxbZLi'kZjs[kk+x v{kls45º dks.kcukrhgksrksk dk
eku gksxkA
(A*)
1
2
(B)
1
4
(C) 2 (D) 4
Soln. (A) 2 45ody
k x tan
dx
 
At x = 1 ij 2k(1) = 1
1
2
k 
22. It is given that A R B 
  
and R A
 
. Then the angle between A & B
 
is
A R B 
  
rFkkR A
 
fn;kgqvkgS]rksA & B
 
dse/; dks.kgksxkA
(A) 1 A
cos
R
  
  
(B) 1 B
cos
A
  
  
(C*) 1 R
tan
A
  
  
(D) 1 R
sin
A
  
  
Soln. (C)

10. Page No.-2
B
a
®
A
®
R
tan =
R
A
 = tan–1
R
A
23. If there are two vectors A and B
 
such that 2ˆ ˆ ˆA B i j k   
 
and ˆ ˆA B (i k)  
 
, then the angle between
A and B
 
is .
;fn nkslfn'k

A rFkk

B bl izdkj gSfd 2ˆ ˆ ˆA B i j k   
 
rFkk ˆ ˆA B (i k)  
 
gS, rks

A rFkk

B dse/; dks.k
gksxk
(A) 30o
(B) 45o
(C*) 60o
(D) 120o
Soln. (C) After solving gy djusij :-
ˆ ˆ2A = 2i +2j

ˆ ˆ2B = 2j+2k

ˆ ˆA i j 

, ˆ ˆB j k 

A.B
cos
AB
 
 
1
2
cos   60o
  
24. A particle moves in a straight line. Its speed (v) increases linearly with time. If the initial speed of the
particle is vo and its speed at t = 4 sec is 4vo, then
4
0
vdt is equal to
,d d.kljy js[kkij xfr'khy gSA bldhpky (v) le; dslkFkjs[kh; :i lsc<+rhgSA ;fn d.kdhizkjfEHkd
pky vo rFkk t = 4 lSd.M ij pky 4vo gksrks
4
0
vdt dkeku gksxkA
(A) 4 ov (B) 6 ov (C) 8 ov (D*) 10 ov
Soln. (D) acceleration Roj.k= a
4v0 = v0 + a (4)
a =
4
03v
 
4 4
0 0
0 0
3vdt v v t dt  
4
2
0
31
4 4
2 4
o
o
V
Vdt S V ( ) ( )
 
    
 

= 10 ov
25. A ball is thrown vertically upwards. The velocity at one fourth of the maximum height is 10 3 m/s. then
the velocity with which the ball was thrown is .

11. Page No.-3
,d xsan Å /okZ/kj Å ij dhrjQ iz{ksfir dhtkrhgSA vf/kdre~Å WpkbZdh,d pkSFkkbZÅ WpkbZij bldkosx
10 3 m/s gksrksxsan dkiz{ksi.kosx gksxkA
(A) 5 m/s (B) 10 m/s (C) 15 m/s (D*) 20 m/s
Soln. (D) Let u be velocity of throwing and h be maximum height.
ekuku iz{ksi.kosx rFkkh vf/kdre~Å WpkbZgSA
Then rc
2
u
h
2g

2 2
V u 2as  
u
h
10 3 m/s
h
4
2 2 h
(10 3 ) u 2( g)
4
 
     
2
2 u300 u 2g.
2g(4)
  
2
u 400 u 20m/s    .
26. A particle is moving on a curve given by y = 2 sin2x( x& y are in meters). The x-component of velocity is
always 2 m/s. If the particle starts from origin at t = 0, then displacement (in meters) of the particle from
t = o to
2
t sec

 is
,d d.koØ y = 2 sin2x( x rFkky ehVj esagSA) ij xfr'khy gSA osx dkx ?kVd ges'kk2 m/s jgrkgSA ;fn t = 0
ij d.kewy fcUnqlsxfr izkjEHkdjrkgksrkst = o ls
2

t lSd.M rd d.kdkfoLFkkiu (ehVj esa) gksxkA
(A*)  m (B) 2 m (C) 0 m (D)
2

m
Soln. (A) 2
2
x V x t

    
2 2 0y sin( )   
Displacement foLFkkiu = 
27. A particle is moving along a straight line with uniform acceleration 2
5 m / s and initial velocity 12.5
m/s. then distance travelled by it in 3rd second of motion is
,d d.klh/khjs[kkij le:i Roj.k 2
5 m / s rFkkizkjfEHkd osx 12.5 m/s ds}kjkxfr'khy gSA 3rd (rhljs)
lSd.M esaxfr dsnkSjku blds}kjkr; dhxbZnwjhKkr djksA
(A) 1 m (B) 0 (C*) 1.25 m (D) 2 m

12. Page No.-4
Soln. (C) V = u + at = 0
12 5 5 0. t  
t = 2.5 sec
V = 0
t = 2 sec 2.5 m/s
t = 3 sec
2 5t . sec  (i-e particle turns back)
2 5 t . sec (vFkkZr~d.kokil ykSVsxkA)
Distance travelled in 3rd sec
3rd lSd.M esar; nwjh
2.5 10 1
2
2 2
   
   
   
= 1.25 m
28. A particle is projected with speed u m/s from origin O along y-axis as shown in figure. If the acceleration
of the particle is ˆ ˆ(ai aj) where a is constant, then the equation of trajectory of the particle is
fp=kkuqlkj ,d d.kdksewy fcUnqO lsy v{kdsvuqfn'kpky u m/s ds}kjkiz{ksfir fd;ktkrkgSA ;fn d.kdk
Roj.k ˆ ˆ(ai aj) (tgkWa fu;r gS) gksrksd.kdsiFkdklehdj.kgksxkA
X
Y
u
(A)
2
2
1
2
ax
y
u
 (B*)
2
2 2xu
(y x)
a
  (C)
2
2 2yu
(x y)
a
  (D)
2
2 2 2xu
x y
a
 
Soln. (B) 21
2
x at ……….. (i)
21
2
y ut at  ……….. (ii)
y x
t
u

 , putting in equation (i)
y x
t
u

 , lehdj.k(i) esaj[kusij

2
2 2xu
(y x)
a
 
29. Two particles are projected simultaneously with the same speed u m/s in the same vertical plane with
angles of projection 30º and 60º . At what time (after start) their velocities will become parallel ?
nksd.kksadksleku Å /okZ/kj ry esa,d lkFkleku pky u m/s }kjkØe'k%30º rFkk60º dsiz{ksi.kdks.kij iz{ksfir
fd;ktkrkgSA iz{ksi.kdsfdrusle; i'pkr~budsosx ,d&nwljsdslekUrj gkstk;sxsa?
(A*)
 3 1
u
g
sec (B)
 3 1
u
g
sec (C)
3
u
g
sec (D)
3
2
u
g
sec

13. Page No.-5
Soln. (A)
30 60
30 60
o o
o o
u sin gt u sin gt
u cos u cos
 


 3 1
u
t
g


30. A particle is thrown vertically upwards with initial speed u m/s (with respect to lift) inside a lift moving
downwards with constant velocity. Its time of flight is T sec. Again the particle is thrown vertically
upwards with same initial speed u m/s. (with respect to lift) inside a lift moving upwards with constant
acceleration g/2, then new time of flight is
uhpsdhrjQ fu;r osx lsxfr'khy fy¶V dsvUnj ,d d.kdksfy¶V dslkis{kÅ /okZ/kj Å ij dhrjQ izkjfEHkd
pky u m/s lsiz{ksfir fd;ktkrkgSA bl le; bldkmMM~;u dky T lSd.M gSA vc nwckjkÅ ij dhrjQ fu;r
Roj.kg/2 lsxfr'khy fy¶V dsvUnj d.kdksfy¶V dslkis{kÅ /okZ/kj Å ij dhrjQ leku izkjfEHkd pky u m/s
lsiz{ksfir fd;ktk;srksbl d.kdku;kmM~M;u dky gksxkA
(A)
2
T
sec (B) 2T sec (C)
3
2
T
sec (D*)
2
3
T
sec
Soln. (D)
2u
T
g

2
2
' u
T
g g /


2 2
3
u
g
 
  
 
2
3
T

SECTION-2 : (One or more option correct type)
[k.M–2 : (,d ;kvf/kd lghfod Yi çd kj)
This section contains 5 multiple choice questions. Each question has four choices (A), (B), (C) and
(D) out of which ONE or MORE are correct.
bl [k.M esa5 cgqfod Yi ç'u gSA çR;sd ç'u esapkj fod Yi (A), (B), (C) vkSj (D) gS] ft uesalsd soy ,d ;k
vf/kd lghgSA
MCQ._(5)
31. A particle is projected at an angle  with the horizontal from a point O on a plane which is inclined at an
angle  to the horizontal. The particle is moving horizontally when it strikes the plane at a point A.
,d d.kdksfcUnqO ls{kSfrt ls dks.kij urry ij iz{ksfir fd;ktkrkgSA urry dk{kSfrt lsurdks.k  gSA
;fn urry dhfcUnqA ij d.kdsVdjkrsle; ;g {kSfrt fn'kkesaxfr'khy gksrks
Fixed
A
B
O
u

14. Page No.-6
(A) Time of flight
2usin
T
g

 sec
mMM~;u dky
2usin
T
g

 lSd.M gSA
(B*) Maximum height of the particle
2 2
2
u sin
g

 m
d.kdhvf/kdre~~Å WpkbZ
2 2
2
u sin
g

 ehVjgSA
(C*) Horizontal range OB =
2
u sin cos
g
 
m
{kSfrt ijkl OB =
2
u sin cos
g
 
ehVj gSA
(D*) 1
2tan ( tan )
  
Soln. (B, C, D)
usin
T
g


2u sin ( )
gcos
  


 tan  = 2 tan  , 1
2tan ( tan )
  
2 2
2
max
u sin
H
g


OB (u cos ) (T) =
2
u sin cos
g
 
32. The vectors A

is given by 2ˆ ˆ ˆA ti (sin t) j t k   

where t is time. Then which of the following is (are)
correct ?
lfn'k A

fuEu }kjkfn;ktkrkgSA
2ˆ ˆ ˆA ti (sin t) j t k   

tgkWt le; gS]rksfuEu lsdkSulsfodYi lghgS?
(A*) 1 2A (at t ) 

(B*) 1 2
dA ˆ ˆ ˆ(at t ) i j k
dt
    

(C*)
2
1 2 1
dA
A (at t )
dt
    


(D*) 1 3
dA
A (at t )
dt
 


(A) 1 2 

A (t )ij (B) 1 2    

dA ˆ ˆ ˆ(t ) i j k
dt
ij
(C) 2
1 2 1    

 dA
A (t )
dt
ij (D) 1 3 

 dA
A (t )
dt
ij

15. Page No.-7
Soln. (A, B, C, D)
2ˆ ˆ ˆA t i sin t j t k   

1 ˆ ˆ ˆA(t ) i sin t j k    

2A 

2
dA ˆ ˆ ˆi cos t j tk
dt
    

1 2
dA ˆ ˆ ˆ(t ) (i j k)
dt
    

2
dA ˆ ˆ ˆ ˆ ˆA (i k) (i j) k)
dt
      


ˆ ˆ ˆ( i j k)    
2
2 1
dA
A
dt
   


1 2 3
dA
A.
dt
  


33. A car is travelling north along a straight road at 50 km hr –1
. An instrument in the car indicates that the
wind is directed towards east. If car’s speed is 80 km hr–1
, then instrument indicates that the wind is
directed towards south – east. Then angle made by wind’s direction is given by. [RL - TD]
,d dkj lh/khlM+d ij mÙkj fn'kkdsvuqfn'k50 km hr –1
dhpky lsxfr'khy gSA dkj esayxkgqvk;a=kiznf'kZr
djrkgSfd gokiwoZfn'kkdhrjQ izokfgr gSA ;fn dkj dhpky 80 km hr–1
gksrks;a=kgokdhfn'kknf{k.k&iwoZ
dhrjQ iznf'kZr djrkgSrksgokdhfn'kk}kjkcuk;kx;kdks.kgksxkA
(A) 1 3
tan Nof E
5
  
   
 
(B*) 1 5
tan Nof E
3
  
   
 
(C) 1 1
tan Nof W
2
  
   
 
(D)  = tan–1
(5) N of E
(A) 1 3
tan
5
  
   
 
iwoZlsmÙkj dhrjQ (B*) 1 5
tan
3
  
   
 
iwoZlsmÙkj dhrjQ
(C) 1 1
tan
2
  
   
 
if'pe lsmÙkj dhrjQ (D)  = tan–1
(5) iwoZlsmÙkj dhrjQ
Sol. (B)
WGV

= x y
ˆ ˆV i V j

1WCV

is towards east
1WCV

iwoZdhrjQ
Vx
Vy
50
 Vy
= 50 m/s ; Vx
> 0
2WCV

is towards south-east

16. Page No.-8
2WCV

nf{k.kiwoZdhrjQ
Vx
Vy
80
45°
 Vx
= 30 m/s
50
30
1 5
tan Nof E
3
  
  
 

34. A particle moving in a straight line with constant acceleration has speeds 7 m/s and 17 m/s at A
and B points respectively. If M is the mid-point of AB, then which of the following is (are) correct?
ljy js[kkij fu;r Roj.klsxfr'khy d.kdhfcUnqA rFkkB ij pky Øe'k%7 m/s rFkk17 m/s gSA ;fn AB js[kk
dke/; fcUnqM gksrksfuEu eslsdkSulk@dkSulsfodYi lghgSA
(A*) the speed of particle at M is 13 m/s
M ij d.kdhpky 13 m/s gSA
(B*) the average speed between A and M is 10 m/s
A rFkkM dse/; vkSlr pky 10 m/s gSA
(C) the average speed between M and B is 14 m/s
M rFkkB dse/; vkSlr pky 14 m/s gSA
(D*) the ratio of the time to go from A to M and that from M to B is 3 : 2.
A lsM rd rFkkM lsB rd tkusesafy;sx;sle; dkvuqikr 3 : 2 gSA.
Soln: (A,B,D)
M
x x
A
V=7 V=17
B
  ax27V
22
M  .......(i)
  ax2V17 2
M
2
 .......(ii)
s/m13VM 
  s/m10
2
137
AMVavg 


  s/m15
2
1713
MBVavg 


1ta713 
2at1317  2:3t:t 21 
35. A man swims at a speed   hr/kmjˆ6iˆ3V1  relative to water. If the water flows with a speed
hr/kmiˆ5V2  . If the width of the river is  jˆm500d  .Then
(A*) path of man is straight line. (B*) time of crossing the river is 5 min.

17. Page No.-9
(C) velocity of man is 10 m/s. (D) drift of man in the direction of flow is 600 m.
,d O;fDr ikuhdslkis{kpky   hr/kmjˆ6iˆ3V1  lsrSj ldrkgSA ;fn ikuh hr/kmiˆ5V2  pky lsizokfgr
gSA ;fn unhdhpkSM+kbZ  jˆm500d  gksrks
(A*) O;fDr dkiFkljy js[kh; gSA (B*) unhdksikj djusesayxkle; 5 min gSA
(C) O;fDr dkosx 10 m/s gSA (D) izokg dhfn'kkesaO;fDr dkfoLFkkiu 600 m gSA
Soln: (A, B)
Resultant path of man is straight line.
O;fDr dkifj.kkehiFkljy js[kh; gSA
  hr/kmjˆ6iˆ8VVV RMRM 
s/m
9
25
hr/km10VM 
min5
1000
60
6
500
t 
Drift fopyu m
3
2000
1000
60
5
8  .
SECTION-3 : (Integer value correct Type)
[k.M – 3 : (iw.kk±d eku lghçd kj)
This section contains 5 questions. The answer to each question is a Two digit integer, ranging from
00 to 99 (both inclusive).
bl [k.M esa5 ç'u gSaA çR;sd ç'u dkmÙkj 00 ls99 rd ¼nksuksa'kkfey½dschp dknksvad ksaokykiw.kk±d gSA
Integer_(5)_(Double Digit)
36. A ball is projected with speed 10 m/s from ground at angle 300 with the vertical. After some time it
again fall on the ground, then the magnitude of average velocity of the ball in this interval (in m/s) is
,d xsan dkstehu ls10 m/s dhpky lsÅ /okZ/kj ls30° dks.kij iz{ksfir fd;ktkrkgSA dqN le; i'pkr~;g
okil tehu ij fxjrhgS]rksbl le;kUrjky esaxsan dkvkSlr osx dkifjek.k(m/s esa) Kkr dhft,A
Ans. 05
Soln : (5)
o
avgV ucos 10cos60 5m / s   
37. If c,b,a are three vectors having magnitudes 1, 2, 3 respectively such that a b c 0  
  
then value of
a.cc.bb.a  is :
;fn c,b,a rhu lfn'kksadkifjek.kØe'k%1, 2, 3 bl izdkj gSfd a b c 0  
  
gksrks a.cc.bb.a  dkeku
Kkr dhft, :
Ans. 07
Soln : (7)
0cba 
  0a.cc.bb.a2cba 222

 
2
cba
a.cc.bb.a
222



18. Page No.-10
7
2
941
2
cba
a.cc.bb.a
222





38. A particle moves along the curve x2y2
 where
2
t
x
2
 (x & y are in meters), (t is time in sec). Then
the magnitude of the acceleration of the particle at sec2t  (in m/s
2
) is
,d d.koØ x2y2
 dsvuqfn'kxfr'khy gS;gk¡
2
t
x
2
 gSA (x o y ehVj esagS), (t le; lsd.M esagS) A rksle;
sec2t  ij d.kdsRoj.kdkifjek.k(m/s
2
esa) Kkr dhft,A
Ans. 01
Soln: (1)
2
t
x
2

1at
dt
dx
V xx 
0a1Vtytyx2y yy
222

2
xa a 1 m/s 
39. The velocity of a particle is given by V = (2 + 3x) m/s(x is position in meters). Then the acceleration of
the particle at m
3
2
x  is (in m/s
2
).
,d d.kdkosx V = (2 + 3x) m/s (fLFkfr x ehVj esagS) }kjkfn;ktkrkgSA rks m
3
2
x  ij d.kdkRoj.k(m/s
2
esa) Kkr dhft,A
Ans. 12
Soln : (12)
x96
dx
dv
Va 
  2
s/m1232xata 
40. The velocity vector of a particle moving in xy plane is given by  jˆxiˆtV  where t is time and x is
position. If initially the particle was at origin, and equation of trajectory (path) of the particle is
23
byax  , then the value of (a + b) is
xy ry esaxfr'khy d.kdkosx lfn'k  jˆxiˆtV  }kjkfn;ktkrkgS;gk¡t le; rFkkx fLFkfr gSA ;fn izkjEHk
esad.kewy fcUnqij gksrFkkd.kdsiFkdhlehdj.k 23
byax  }kjknhtk;srks(a + b) dkeku Kkr dhft,A
Ans. 11
Soln: (11)
At t = 0, x = 0, y = 0 ij
jˆxiˆtV 
2
t
xt
dt
dx 2

2
t
x
dt
dy 2

6
t
y
3

Eliminating t dksizfrLFkkfir djusij
23
y9x2  (i-e. equation of path iFkdhlehdj.k)

19. Page No.-11
a = 2, b = 9 11ba 

20. Page #
1
Course : (ELPD ) Test Date : 10.08.2014
Test Type : CT-1
Paper-1 Time Duration : 3 Hrs.
Paper-2 Time Duration : 3 Hrs.
Paper Level - Moderate to Tough
SYLLABUS :
Introduction to chemistry , Atomic structure
( Upto Heisenberg uncertainity principle)
SYLLABUS SCHEDULED
SYLLABUS
SCHEDULED
WEIGHTAGE
(BY FC)
SR.
NO.
TOPIC NAME
(I) (II)
WEIGHTAGE IN
PAPER-1
(BY FACULTY)
WEIGHTAGE IN
PAPER-2
(BY FACULTY)
1.
Introduction to chemistry 30% 30%
2. Atomic structure
( Upto Heisenberg
uncertainity principle)
70% 70%
Organic chemistry
SYLLABUS :
IUPAC nomenclature and Structural isomerism complete.
SYLLABUS SCHEDULED
SYLLABUS
SCHEDULED
WEIGHTAGE
(BY FC)
SR.
NO.
TOPIC NAME
(I) (II)
WEIGHTAGE IN
PAPER-1
(BY FACULTY)
WEIGHTAGE IN
PAPER-2
(BY FACULTY)
1. IUPAC nomenclature and
Structural isomerism
complete
Test Pattern :

21. Page #
2
S.No. Subject Nature of Questions No. of Questions Marks Negative Total
1 to 10 SCQ 10 3 –1 30
11 to 15 MCQ 5 4 0 20
16 to 20 Integer (double digits) 5 4 0 20
21 to 30 SCQ 10 3 –1 30
31 to 35 MCQ 5 4 0 20
36 to 40 Integer (double digits) 5 4 0 20
41 to 50 SCQ 10 3 –1 30
51 to 55 MCQ 5 4 0 20
56 to 60 Integer (double digits) 5 4 0 20
60 210
Paper-1 CT-1
Total Total
Maths
Physics
Chemistry
S .No . S u b je ct N a tu re o f Q u e stio n s N o . o f Q u e stio n s M a rks Ne g a tive T o ta l
1 to 7 M C Q 7 4 0 28
8 to 13 Com prehens ion (3 C om p. x 2 Q .) 6 3 –1 18
14 to 16 M TC 3 8 0 24
17 to 23 M C Q 7 4 0 28
24 to 29 Com prehens ion (3 C om p. x 2 Q .) 6 3 –1 18
30 to 32 M TC 3 8 0 24
33 to 39 M C Q 7 4 0 28
40 to 45 Com prehens ion (3 C om p. x 2 Q .) 6 3 –1 18
46 to 48 M TC 3 8 0 24
48 210
P a p e r-2 C T -1
T o ta l T o ta l
M a th s
P h ysics
C h e m istry
Physical paper1 Organic paper 1
SCQ(6) SCQ(4)
MCQ(3) MCQ(2)
Integer(Double)(3) Integer(Double (2)
Physical paper 2 Organic paper 2
MCQ (4) MCQ(3)
Comp.(3 x 2Q)(2) Comp. (3 x 2Q) (1)
MTC (4 vs 4) (2) MTC((4 vs 4)(1)

22. Page #
3
JEE (ADVANCED) CHEMISTRY PAPER SKELETON
Faculty Name : HM SIR Test Name : JB&JB* (CT-1)
PAPER - 1
S.
No.
TYPE (P) (I) (O) TOPIC(S) SUBTOPIC(S)
DIFFICULTY LEVEL :
Easy (E), Moderate (M),
Tough (T)
41 SCQ (P) Atomic structure Bohr model M
42 SCQ (P) Atomic structure
Photo electric
effect
M
43 SCQ (P) Atomic structure Bohr model E
44 SCQ (P) Mole concept M
45 SCQ (P) Atomic structure de-Broglie T
46 SCQ (P) Mole concept M
47 SCQ (O) IUPAC M
48 SCQ (O) IUPAC M
49 SCQ (O) IUPAC M
50 SCQ (O)
Structural
isomerism
M
51 MCQ (P) Mole concept E
52 MCQ (P) Atomic structure Bohar model M
53 MCQ (P) Atomic structure
H-spectrum de-
Broglie
T
54 MCQ (O) IUPAC M
55 MCQ (O) IUPAC M
56
Double
Integer
Type
(P) Atomic structure Quantum theory M
57
Double
Integer
Type
(P) Atomic structure
Photo electric
effect
E
58
Double
Integer
Type
(P) Mole concept Avg. atomic mass M
59
Double
Integer
Type
(O) IUPAC M
60.
Double
Integer
Type
(O) Isomerism counting M
Faculty preparing the TEST PAPER should fill it according to paper pattern and submit it with finalisaion of
paper at SMD.

23. Page #
4
Physical paper-1
SCQ(6)
41. The ratio of area of 4
th
circular orbit of He+ ion to that of 3
rd
orbit of Li2+ ion is : (ATS(P))
He+ vk;u d h 4
th
o Li2+ v k;u d h 3
rd
o`Ùkkd kj d {kk d s{ks=kQ y d k vuqikr fuEu gS&
(A*) 64 : 9 (B) 4 : 3 (C) 8 : 3 (D) 3 : 4
Sol.
4 2
A B
4 2
B A
n Z
n Z
=
4 2
4 2
4 3
3 2


=
64
9
2
2 n
area r , r
Z
  
   
  
2
2 n
r , r
Z
  
   
  
{ks=kQy
42. Light of wavelength 2 falls on a metal having work function hc/0. Photoelectric effect will take
place only if: (ATS(P))
d k;Z Q y u hc/0 ;qDr ,d /kkrq ij 2rjax}S/;Z d k izd k'k vkifrr gksrk gSA izd k'k fo| qr
izHkko d soy rHkh mRiUu gksxk t c%
(A)  0 (B)  20 (C*) 2  0 (D)  0 / 2
Sol.
43. An electron in a hydrogen like species jumps from an energy level to another energy level in such
a way that its kinetic energy changes from 'a' to
a
4
. The change in total energy of electron will be :
,d gkbMªkstu leku Lih'kht esa,d bysDVªkWu ,d Å tkZLrj lsvU; Å tkZLrj esabl izdkj LFkkukUrfjr
gksrkgS]fd bldhxfrt Å tkZ'a' ls
a
4
rd ifjofrZr gksrhgS]rksbldhdqy Å tkZesaifjorZu gksxk:
(ATS(P))
(A*) +
3
4
a (B) –
3
8
a (C) +
3
2
a (D) –
3
4
a
Sol. Change in total energy =
a
– – ( a)
4

dqy Å tkZesaifjorZu =
a
– – ( a)
4

=
3
a
4

44. LPG contains n-butane and isobutane. Mass of carbon in 14.5 Kg of LPG.
LPG n-C;wVsu o vkblksC;wVsu j[krkgSA LPG ds14.5 Kg esadkcZu dknzO;eku fuEu gS&
(Mole-1(P))
(A) 3 Kg (B*) 12 Kg (C) 14.5 Kg (D) 10 Kg
Sol. mass of Carbon dkcZu dknzO;eku =
14.5
48
58

= 12 Kg
45. Calculate ratio of de-Broglie wavelength of O2 molecule to He atom if ratio of their kinetic energy
is 1 : 18.
O2 v.kqo He ijek.kqdh Mh&czksXyh rjax}S/;Zdk vuqikr ifjdfyr dhft, ;fn budh xfrt Å tkZdk
vuqikr 1 : 18 gksa&
(A) 1:23 (B*) 3 : 2 (C) 2 : 3 (D) 23:1

24. Page #
5
Sol. 2O =
1KE322
h
 & He =
2KE42
h

He
O2


=
1
2
KE32
KE4
= 132
184


=
2
3
.
46. Which of the following has maximum volume at STP - (Mole-1(P))
STP ij fuEu esalsfdldkvk;ru vf/kdre gksrkgS&
(A) 2 gm molecules of CH4 (B) 28 gm of CO
(C*) 5 gm H2 (D) 200 gm of H2O
STP ij fuEu esalsfdldkvk;ru vf/kdre gksrkgS&
(A) 2 gm CH4 v.kq (B) 28 gm CO v.kq
(C*) 5 gm H2 v.kq (D) 200 gm H2O v.kq
Sol. (A) volume of CH4 = 2  22.4 = 44.8 liter.
(B) volume of CO = 1  22.4 = 22.4 liter.
(C) volume of H2 = 2.5  22.4 = 56 liter.
(D) volume of H2O = 200 ml.
Sol. (A) CH4 dkvk;ru = 2  22.4 = 44.8 yhVj.
(B) CO dkvk;ru 1  22.4 = 22.4 yhVj.
(C) H2 dkvk;ru = 2.5  22.4 = 56 yhVj.
(D) H2O dkvk;ru = 200 ml.
SCQ(4)
47. IUPAC name of compound
Cl
Br
is (IUPAC(O))
(A) 7-Bromo-3-chloro-5-(1,1-dimethylethyl)-3-ethyl-7-methyl-5-(2-methylpropyl)nonane
(B*) 3-Bromo-7-chloro-5-(1,1-dimethylethyl)-7-ethyl-3-methyl-5-(2-methylpropyl)nonane
(C) 3-Bromo-7-chloro-7-ethyl-3-methyl-5-(1,1-dimethylethyl)-5-(2-methylpropyl)nonane
(D) 3-Bromo-5-(1,1-dimethylethyl)-5-(2-methylethyl)-7-chloro-7-ethyl-3-methylnonane
Cl
Br
;kSfxd dkIUPAC uke gS
(A) 7-czkseks-3-Dyksjks-5-(1,1-MkbZesfFky,fFky)-3-,fFky-7-esfFky-5-(2-esfFkyizksfiy) uksusu
(B*) 3-czkseks-7-Dyksjks-5-(1,1-MkbZesfFky,fFky)-7-,fFky-3-esfFky-5-(2-esfFkyizksfiy) uksusu
(C) 3-czkseks-7-Dyksjks-7-,fFky-3-esfFky-5-(1,1-MkbesfFky,fFky)-5-(2-esfFkyizksfiy)uksusu
(D) 3-czkseks-5-(1,1-MkbesfFky,fFky)-5-(2-esfFky,fFky)-7-Dyksjks-7-,fFky-3-esfFkyuksusu

25. Page #
6
Sol.
3-Bromo-7-chloro-5-(1,1-dimethylethyl)-7-ethyl-3-methyl-5-(2-methylpropyl)nonane
3-czkseks-7-Dyksjks-5-(1,1-MkbZesfFky,fFky)-7-,fFky-3-esfFky-5-(2-esfFkyizksfiy) uksusu
48. The IUPAC name of HO–C–COOH
|
|
CH2–COOH
CH2–COOH
is (IUPAC(O))
;kSfxd HO–C–COOH
|
|
CH2–COOH
CH2–COOH
dklghIUPAC uke gS%&
(A) 3-Carboxy-3-hydroxypentanedicarboxylic acid
(B) 2-Hydroxypropane-1,2,3-trioic acid
(C) 3-Hydroxypropane-1,2,3-tricarboxylic acid
(D*) 2-Hydroxypropane-1,2,3-tricarboxylic acid
(A) 3-dkcksZDlh-3-gkbMªksDlhisUVsuMkbdkcksZfDlfyd vEy
(B) 2-gkbMªksDlhizksisu -1,2,3-VªkbZvksbd vEy
(C) 3- gkbMªksDlhizksisu -1,2,3- VªkbZdkcksZfDlfyd vEy
(D*) 2- gkbMªksDlhizksisu -1,2,3- VªkbZdkcksZfDlfyd vEy
Sol. HO–C–COOH
|
|
CH2–COOH
CH2–COOH
1
2
3
2-Hydroxypropane-1,2,3-tricarboxylic acid
gy% HO–C–COOH
|
|
CH2–COOH
CH2–COOH
1
2
3
2- gkbMªksDlhizksisu -1,2,3- VªkbZdkcksZfDlfyd vEy
49. The IUPAC name of CH–CCl3
Cl
Cl
is (IUPAC(O))

26. Page #
7
CH–CCl3
Cl
Cl
;kSfxd dklghIUPAC uke gS%
(A) Dichlorodiphenyltrichloroethane
(B) Trichloromethylbis-(4 chlorophenyl) methane
(C*) 1,1,1-Trichloro-2,2-bis(4-chlorophenyl) ethane
(D) 2,2,2-Trichloro-1,1-bis(4-chlorophenyl) ethane
(A) MkbZDyksjksMkbQSfuy MªkbZDyksjks,sFksu
(B) VªkbZDyksjksesfFkyfcl-(4 DyksjksQsfuy) esFksu
(C*) 1,1,1-VªkbZDyksjks-2,2-fcl (4-DyksjksQsfuy) ,sFksu
(D) 2,2,2-VªkbZDyksjks-1,1-fcl (4-DyksjksQsfuy) ,sFksu
Sol. CH–CCl3
Cl
Cl
12
1,1,1-Trichloro-2,2-bis(4-chlorophenyl) ethane
1,1,1- VªbZDyksjks-2,2-fcl (4-DyksjksQsfuy) ,sFksu
50.
CHO
COOCH3
and CHO
COOH
are :
(Isomerism(O))
(A) Identical compounds (B) Positional isomer
(C*) Functional isomer (D) Chain isomer
CHO
COOCH3
rFkk CHO
COOH
gS:
(A) le:ih;kSfxd (B) fLFkfr leko;oh
(C*) fØ;kRed leko;oh (D) J`a[kykleko;oh
Sol. Both compounds having same molecular formula but different functional group.
nksuksa;kSfxdksadsv.kqlw=kleku gSysfdu fØ;kRed lewg fHkUu&fHkUu gSA
MCQ(3)
51. Which of the following samples contain 5 NA atoms : (Mole-1(P))
(A*) 22.4 L of CH4 at STP (B*) 1 gram molecules of N2O3
(C*) 1.25 moles of P4 (D) 0.5 NA molecules of Ethene (C2H4)
fuEu esalsdkSulsuewus5 NA ijek.kqj[krsgSa%
(A*) STP ij 22.4 L CH4 (B*) N2O3 ds1 xzke v.kq
(C*) 1.25 eksy P4 (D) ,Fkhu (C2H4) ds0.5 NA v.kq

27. Page #
8
Sol. (A) mole of CH4 = 1
number of atoms = 5NA
(B) mole of N2O3 = 1
number of atoms = 5NA
(C) mole of P4 = 1.25
number of atoms = 5NA
(D) number of atoms in C2H4 = 3NA
Sol. (A) CH4 dseksy = 1
ijek.kqvksadhla[;k= 5NA
(B) N2O3 dseksy = 1
ijek.kqvksadhla[;k= 5NA
(C) P4 dseksy = 1.25
ijek.kqvksadhla[;k= 5NA
(D) C2H4 esaijek.kqvksadhla[;k= 3NA
52. Which of the following options is/are independent of both n and Z ? (ATS(P))
Un = Potential energy of electron in nth orbit
KEn = Kinetic energy of electron in nth orbit
n = angular momentam of electron in nth orbit
vn = Speed of electron in nth orbit
fn = Frequency of revolution of electron in nth orbit
Tn = Time period of revolution of electron in nth orbit
fuEu esalsdkSulsfodYi n rFkkZ nksuksaij fuHkZj ughdjrkgS@gSa
Un = nth d{kkesabysDVªkWu dhfLFkfrt Å tkZ
KEn = nth d{kkesabysDVªkWu dhxfrt Å tkZ
n = nth d{kkesabysDVªkWu dkdks.kh; laosx
vn = nth d{kkesabysDVªkWu ds?kw.kZu dhxfr
fn = nth d{kkesabysDVªkWu ds?kw.kZu dhvko`fÙk
Tn = nth d{kkesabySDVªkWu ds?kw.kZu dkvkorZdky
(A*)
n
n
U
KE
(B*)
n
nn vr


(C*) nn FT  (D*) 2
n
nn
v
f
Sol. (A) n
n
KE
U
= –
1
2
(B) n n
n
r v

=
2
n
z

z
n

1
n
= 1
(C) Tn fn =
3
2
n
z

2
3
z
n
= 1
(D) n n
2
n
f
v

=
2
3
n z
n


2
2
n
z
= 1
53. Electron in a sample of H atoms are returned to ground state from an excited state so that change
in de-Broglie wavelength of electron corresponding to the transition of maximum energy = (  8
0.529) Å. Select correct options (ATS(P))
(A*) Number of orbit of original excited state is 5.
(B) Total number of different spectral lines in visible region is 4.
(C*) Total number of different spectral lines in infrared region is 3.
(D*) Change in angular momentum of electron corresponding to the transition of minimum energy
= 

28. Page #
9
,d izkn'kZesabySDVªkWu ,d mÙksftr voLFkk lsvk| voLFkk esaykSVdj vkrsgSarkfd vf/kdre Å tkZdh
laØe.kdslaxr bySDVªkWu dhMh&czksXyhrjax}S/;ZesaifjorZu = (  8 0.529) Å. gkstk,A lghfodYi dk
p;u dhft,A
(A*) ewy mÙksftr voLFkkdsfy, d{kkdhla[;k5 gSA
(B) n`'; {ks=kesafofHkUu LiSDVªy js[kkvksadhdqy la[;k4 gSA
(C*) vojDr {ks=kesafofHkUu LiSDVªy js[kkvksadhdqy la[;k3 gSA
(D*) U;wure Å tkZdslaØe.kdslaxr bySDVªkWu dsdks.kh; laosx esaifjorZu =  gSA
Sol.
n
1
 = 02 r
z

(n–1)
 n – 1 = 4
n = 5.
Total number of lines in IR region = 3.
IR {ks=kesajs[kkvksadhdqy la[;k= 3
Change in angular momentam (5  4) =
h
2
= 
dks.kh; laosx esaifjorZu (5  4) =
h
2
= 
MCQ(2)
54. Which of the following is/are represent correct IUPAC name?
(IUPAC(O))
(A*)
NC
C=C
CN
CN
NC
Ethenetetracarbonitrile
(B*)
CHO
|
CHO
Ethanedial
(C*)
CHO
CHO
CHOOHC Methanetetracarbaldehyde
(D*)
O
O
O
O
3,3-Di(1-Oxoethyl)pentane-2,4-dione
fuEu esalsdkSulk@dkSuls;kSfxdksadsle{kfn;sx;sIUPAC uke lghgS
(A*)
NC
C=C
CN
CN
NC
,sFkhuVsVªkdkcksZukbVªkby
(B*)
CHO
|
CHO
,FksuMkb,sy

29. Page #
10
(C*)
CHO
CHO
CHOOHC esFksuVsVªkdkcsZfYMgkbM
(D*)
O
O
O
O
3,3-MkbZ(1-vkWDlk,fFky) isUVsu -2,4-MkbZvksu
Sol. (A)
NC
C=C
CN
CN
NC
12
Ethenetetracarbonitrile
(B)
CHO
|
CHO1
2
,Fksu Mkb,sy
(C)
CHO
CHO
CHOOHC 1 Methanetetracarbaldehyde
(D)
O
O
O
O 1
234
5
3,3-Di(1-Oxoethyl)pentane-2,4-dione
gy% (A)
NC
C=C
CN
CN
NC
12
,sFkhuVsVªkdkcksZukbVªkby
(B)
CHO
|
CHO1
2
,FksuMkbZ,sy
(C)
CHO
CHO
CHOOHC 1 esFksuVsVªkdkcsZfYMgkbM
(D)
O
O
O
O 1
234
5
3,3-MkbZ(1-vkWDlk,fFky) isUVsu -2,4-MkbZvksu
55. and
Which is/are true about above two structures. (IUPAC & Structural Isomers(O))
(A*) Index of hydrogen deficiency of each is 3
(B*) Both are metamers.

30. Page #
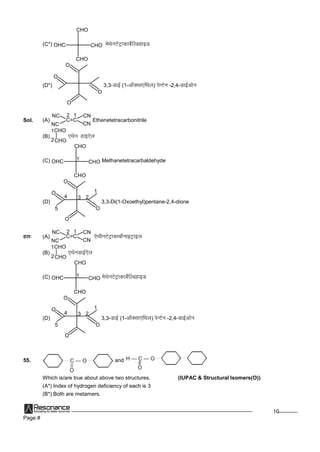
11
(C) Both are chain isomers
(D*) Both have same general formula.
rFkk
mijksDr nkslajpukvksadsfy, dkSulk@dkSulsdFku lR; gS%
(A*) izR;sd esagkbMªkstu U;wurkdklwpdkad rhu gSA
(B*) nksuksae/;ko;ohgSaA
(C) nksuksaJ`a[kykleko;ohgSaA
(D*) nksuksaleku lkekU; lw=kj[krsgSaA
Integer(Double)(3)
56. An LED of powers X watt emits twice as many photons at 1000 nm as another LED of power 5
watt at 400 nm in one second. Find X.
(ATS(P))
1 lSd.M esaX okWV 'kfDr dh,d LED }kjkmRlftZr 1000 nm dsQksVksuksadhla[;k]5 okWV 'kfDr dhvU;
LED }kjkmRlftZr 400 nm dsQksVksuksadhla[;kdhrqyukesanqxquhgksrhgS]rc X Kkr dhft,A
Ans. 04
Sol. Time = 1 second LED 1 ; 15
2LED

Energy = X × 1 = XJ ; 5J
 = 1000 nm ;  = 400 nm
no. of photons = 2n ; no. of photon = n

1000
hc
n2X  ;
400
hc
n5 
 
1000
54002
X

 = 4.
Sol. le; = 1 lSd.M LED 1 ; 15
2LED

Å tkZ= X × 1 = XJ ; 5J
 = 1000 nm ;  = 400 nm
QksVkWuksadhla[;k= 2n ; QksVkWuksadhla[;k= n

1000
hc
n2X  ;
400
hc
n5 
 
1000
54002
X

 = 4.
57. Threshold frequency of a metal is 0. When light of frequency  = 30 is incident on the metal
plate, maximum kinetic energy of emitted photoelectron is x. When frequency of incident radiation
is 50, kinetic energy of emitted photoelectron is y. If threshold energy of metal is z. Find value of
2
z
yx





 
: (ATS(P))

31. Page #
12
,d /kkrqdh nsgyhvko`fÙk0 gSA tc /kkrqIysV ij vko`fÙk = 30 dk izdk'k vkifrr gksrk gS]rksmRlftZr
izdk'k]bySDVªkWu dh vf/kdre xfrt Å tkZx gSA tc vkifrr fofdj.k dh vko`fÙk 50 gS]rksmRlftZr izdk'k
bySDVªkWu dhxfrt Å tkZy gSA ;fn /kkrqdhnsgyhÅ tkZz gS]rks
2
z
yx





 
dkeku Kkr dhft,A
Ans. 36
Sol. 0 0 0x 3h h 2h     
0 0 0y 5h h 4h     
0z h 

2
x y
z
 
 
 
= 36.
58. An element exist in three isotopic form : 60A, 62A and 64A.
Relative abundance of 60A = 30% by mole.
If average atomic mass of ‘A' is 62.6 u, find out the sum of % abundance (by mole)
of 60A and 64A. (Mol-1)(P))
;fn ,d rRo]rhu leLFkkfud :i 60A, 62A rFkk64A esaik;ktkrkgSA
60A dhvkisf{kd ckgqY;rk= 30%
;fn ‘A' dk vkSlr ijek.oh; nzO;eku 62.6 u gS]rks60A o 64A dh izfr'kr ckgqY;rk ¼eksy@eksy esa½ dk
;ksx Kkr dhft,&
Ans. 90
Sol. Average atomic mass =
(30 60) (70 x)62 (x 64)
100
    
 x = 60%
 mole% of
60
A + mole% of
64
A = 90
Sol. vkSlr ijek.oh; nzO;eku =
(30 60) (70 x)62 (x 64)
100
    
 x = 60%

60
A dkeksy % +
64
A dkeksy % = 90
Integer(Double)(2)
59. The sum of number of functional group and index of hydrogen deficiency in the following
compound is -
fuEu ;kSfxd easfØ;kRed lewg o gkbMªkstu U;wurkdklwpdkad dhla[;kdk;ksx gSA
(IUPAC(O))
OH
O
N
NH2 COOH
Ans. 19
Sol. Index of hydrogen deficiency = 15
Functional group = 4
gkbMªkstu U;wurkdklwpdkad = 15
fØ;kRed lewg = 4
60. How many isomers are possible of molecular formula C7H16 having word root pent.
(Isomerism(O))
C7H16 v.kqlw=kj[kusokys;kSfxd ftldkewy 'kCn isUV gS]dsfdrusleko;ohlEHko gS
Ans. 05

32. Page #
13
Sol. C–C–C–C–C
|
|
C
C
C–C–C–C–C
|
C
|
C
C–C–C–C–C
|
C
|
C
C–C–C–C–C
|
|
C
C
C–C–C–C–C
|
C
|
C