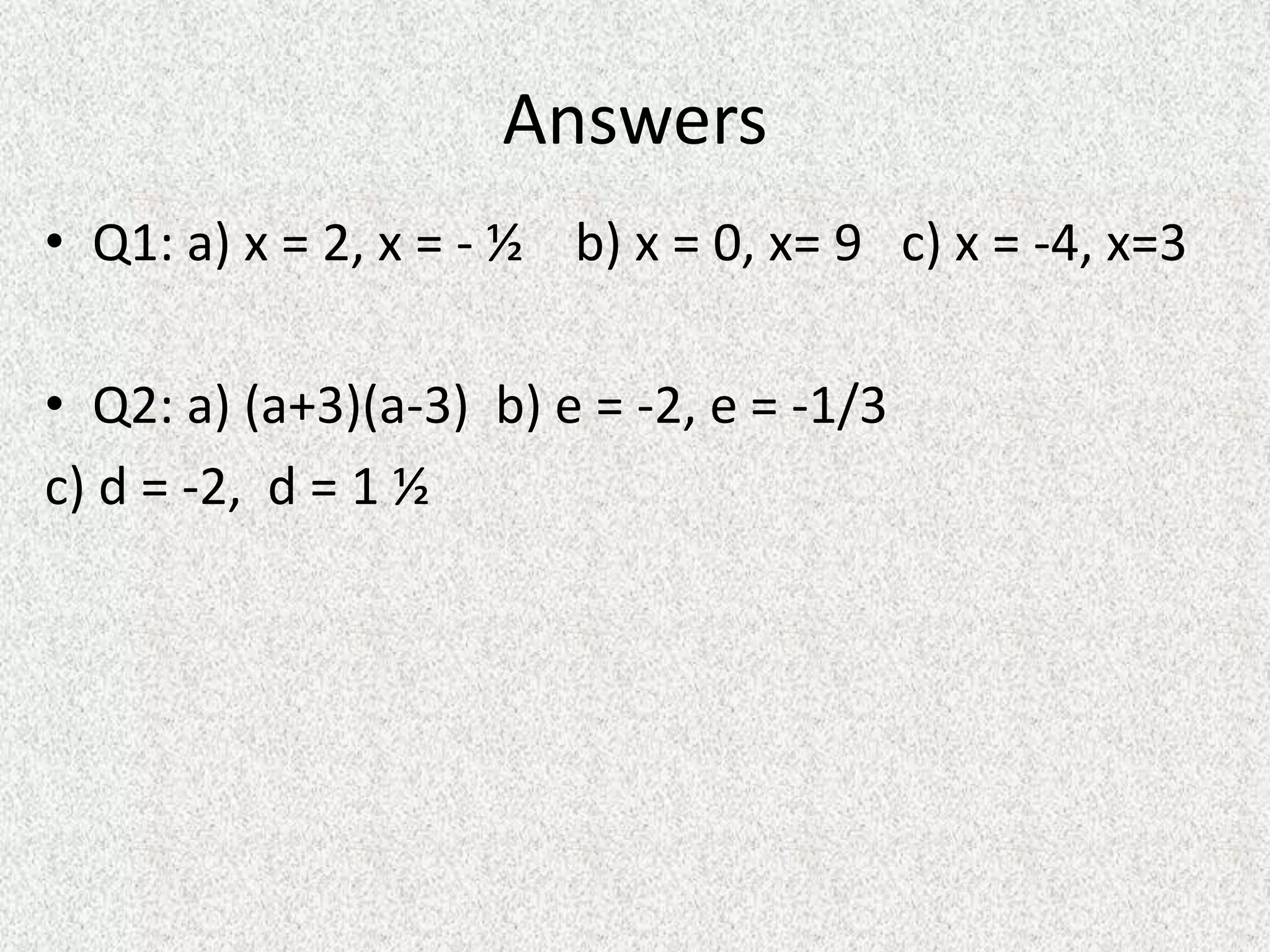The document discusses solving quadratic equations by factoring. It provides examples of factoring quadratic expressions and setting each factor equal to 0 to solve for the roots. Methods include identifying factors of constants, using the zero factor property, and checking solutions. It also applies these skills to word problems involving quadratic equations.

1. Equations and Quadratic
functions
Objective
Solving quadratic equation by
Factorisation

2. Warm up
• Solve the given equation.
y
y
y
y
y





2
1
6
3
6
3
511
3
115
3

3. Explanation

4. 11.6 – Solving Quadratic Equations by Factoring
A quadratic equation is written in the Standard
Form, 2
0ax bx c  
where a, b, and c are real numbers and .0a 
Examples:
2
7 12 0x x  
2
3 4 15x x 
 7 0x x 
(standard form)

5. Zero Factor Property:
If a and b are real numbers and if ,0ab 
Examples:
 7 0x x 
then or .0a  0b 
0x  7 0x  
7x  0x 
11.6 – Solving Quadratic Equations by Factoring

6. Zero Factor Property:
If a and b are real numbers and if ,0ab 
Examples:
  10 3 6 0x x  
then or .0a  0b 
10 0x   3 6 0x 
10x 
3 6x  2x 
10 10 01 0x    63 66 0x   
3 6
3 3
x

11.6 – Solving Quadratic Equations by Factoring

7. Solving Quadratic Equations:
1) Write the equation in standard form.
4) Solve each equation.
2) Factor the equation completely.
3) Set each factor equal to 0.
5) Check the solutions (in original equation).
11.6 – Solving Quadratic Equations by Factoring

8. 2
3 18 0x x  
6 0x  3 0x  
 3x
6x 3x  
2
3 18x x 
18:Factors of
1,18 2, 9 3, 6
   
2
6 3 16 8 
36 18 18 
18 18
   
2
13 3 83  
9 9 18 
18 18
 6x 0
11.6 – Solving Quadratic Equations by Factoring

9.  3 18x x 
18x 
2
3 18x x 
   
2
18 13 18 8 
324 54 18 
270 18
   
2
21 23 11 8 
441 63 18 
378 18
3 18x 
3 183 3x  
21x 
If the Zero Factor
Property is not used,
then the solutions will
be incorrect
11.6 – Solving Quadratic Equations by Factoring

10. 2
4 5x x 
1 0x  5 0x  
  1 5 0x x  
1x   5x 
 4 5x x  
2
4 5 0x x  
11.6 – Solving Quadratic Equations by Factoring

11. 2
3 7 6x x  3 0x   3 2 0x 
  3 3 2 0x x  
3x  
2
3
x 
 3 7 6x x  
2
3 7 6 0x x   3 2x 
6:Factors of
2, 31, 6
3:Factors of
1, 3
11.6 – Solving Quadratic Equations by Factoring

12. 2
9 24 16x x  
2
9 24 16 0x x  
3 4 0x 
  3 4 3 4 0x x  
4
3
x 
3 4x 
 9 16and are perfect squares
11.6 – Solving Quadratic Equations by Factoring

13. 3
2 18 0x x 
2x
2 0x 
2x
3x  
3 0x   3 0x 
3x 0x 
 2
9x  0
 3x  3x 0
11.6 – Solving Quadratic Equations by Factoring

14.   2
3 3 20 7 0x x x   
 3x
3 0x  
7x 
7 0x   3 1 0x 
1
3
x  
3x   3 1x  
3:Factors of 1, 3 7:Factors of 1, 7
 7x  0 3 1x 
11.6 – Solving Quadratic Equations by Factoring

15. Continuous assessment
• Q1: Solve these equations by factorisation.
a) (x-2)(2x+1) = 0
b) 3x2 – 27x = 0
c) 2x2 – 7x + 6 = 0
Q2: a) 2(d2 – 3d +3) = d + 1
b) 3(e + 1)2= 1 – e
c) (g + 3)(2 – g) = g2

16. Answers
• Q1: a) x = 2, x = - ½ b) x = 0, x= 9 c) x = -4, x=3
• Q2: a) (a+3)(a-3) b) e = -2, e = -1/3
c) d = -2, d = 1 ½

17. Final assessment
• Solve by factorisation.
17x2 – 51x + 34 = 0

18. Hard Questions

19. 0 
A cliff diver is 64 feet above the surface of the
water. The formula for calculating the height (h)
of the diver after t seconds is: 2
16 64.h t  
How long does it take for the diver to hit the
surface of the water?
0 
0 
2 0t   2 0t  
2t   2t  seconds
2
16 64t 
16  2
4t 
16  2t   2t 
11.7 – Quadratic Equations and Problem Solving

20. 2
x
The square of a number minus twice the number
is 63. Find the number.
 7x 
7x  
x is the number.
2
2 63 0x x  
7 0x   9 0x  
9x 
2x 63
63:Factors of 1, 63 3, 21 7, 9
 9x 0
11.7 – Quadratic Equations and Problem Solving

21.  5 176w w 
The length of a rectangular garden is 5 feet more than
its width. The area of the garden is 176 square feet.
What are the length and the width of the garden?
 11w
The width is w.
11 0w 
11w
The length is w+5.l w A 
2
5 176w w 
2
5 176 0w w  
16 0w 
16w 
11w 11 5l  
16l 
feet
feet
176:Factors of
1,176 2, 88 4, 44
8, 22 11,16
 16w 0
11.7 – Quadratic Equations and Problem Solving

22. x
Find two consecutive odd numbers whose product is
23 more than their sum?
Consecutive odd numbers: x
5x   5x 2
2 2 25x x x  
2
25 0x  
 5x
5 0x   5 0x  
5, 3  5, 7
5 2 3    5 2 7 
2.x 
 2x   2x x  23
2
22 2 2 25xx x x x  
2
25 2525x  
2
25x 
 5x 0
11.7 – Quadratic Equations and Problem Solving

23. a x
The length of one leg of a right triangle is 7 meters less than
the length of the other leg. The length of the hypotenuse is
13 meters. What are the lengths of the legs?
12a 
 .Pythagorean Th
 
22 2
7 13x x  
5x  
5
meters
7b x  13c 
2 2
14 49 169x x x   
2
2 14 120 0x x  
 2
2 7 60 0x x  
2
5 0x   12 0x 
12x 
12 7b   meters
2 2 2
a b c 
60:Factors of 1, 60 2, 30
3, 20 4,15 5,12
 5x  12x 0
6,10
11.7 – Quadratic Equations and Problem Solving