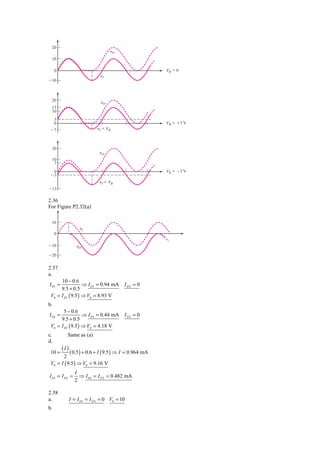
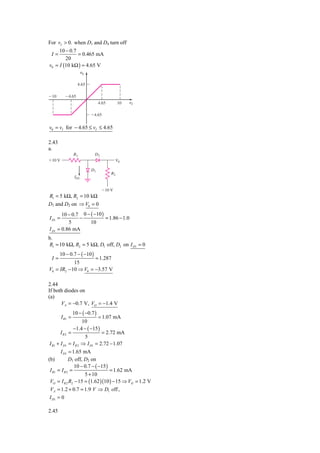
This document contains solutions to various circuit analysis problems. Problem 2.1 solves for the output voltage of a voltage divider circuit given input and resistor values. Problem 2.2 analyzes a circuit with a diode and calculates the output voltage as a function of the input voltage and diode characteristics. The remaining problems continue analyzing circuits involving resistors, diodes, capacitors and calculating values such as output voltage, current, power dissipation and more. Equations are provided and used to solve for unknown variables in each circuit.

1. Chapter 2
Problem Solutions
2.1
␯I ␯0
Rϭ1K
␯I
10
0
Ϫ10
Vγ = 0.6 V, rf = 20 Ω
⎛ R ⎞
⎜ R + r ⎟(
For vI = 10 V, v0 = ⎜ 10 − 0.6 )
⎟
⎝ f ⎠
⎛ 1 ⎞
=⎜ ⎟ ( 9.4 )
⎝ 1 + 0.02 ⎠
v0 = 9.22
10
0.6
␯0
9.22
2.2
ϩ ␯D Ϫ
␯I ␯0
D
R
v0 = vI − vD
⎛i ⎞ v
vD = VT ln ⎜ D ⎟ and iD = 0
⎝ IS ⎠ R
⎛ v ⎞
v0 = vI − VT ln ⎜ 0 ⎟
⎝ IS R ⎠
2.3
80sin ω t
(a) vs = = 13.33sin ω t
6
13.33
Peak diode current id (max) =
R

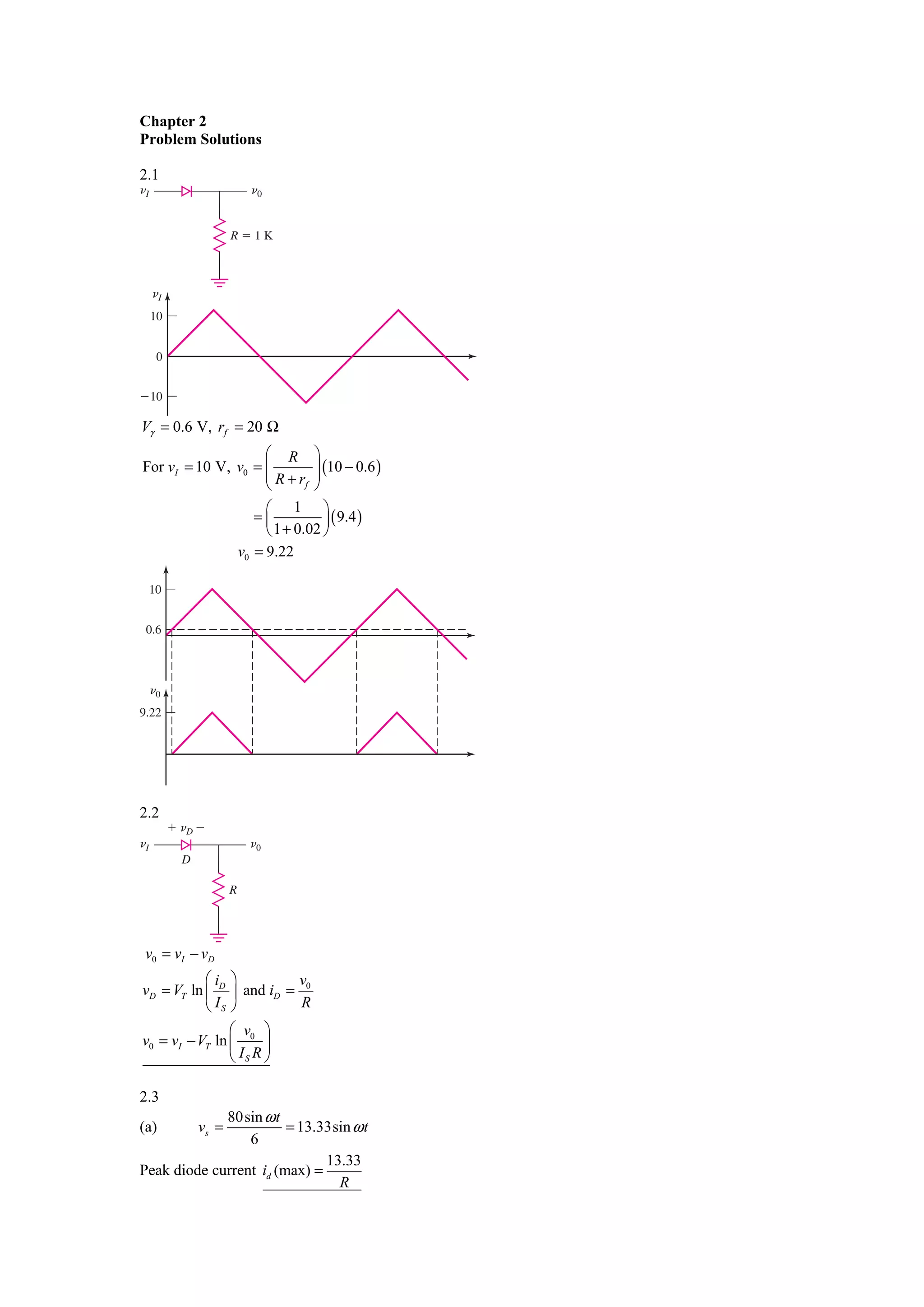
2. (b) PIV = vs (max) = 13.3 V
(c)
To π
1 1
vo ( avg ) = ∫ v (t )dt = 2π ∫ 13.33sin × dt
o
To o o
13.33 13.33 13.33
[ − cos x ]o =
π
= ⎡ − ( −1 − 1) ⎤ =
⎣ ⎦
2π 2π π
vo ( avg ) = 4.24 V
(d) 50%
2.4
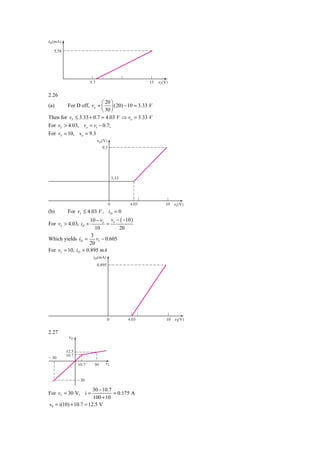
v0 = vS − 2Vγ ⇒ vS ( max ) = v0 ( max ) + 2Vγ
a. For v0 ( max ) = 25 V ⇒ vS ( max ) = 25 + 2 ( 0.7 ) = 26.4 V
N1 160 N
= ⇒ 1 = 6.06
N 2 26.4 N2
b. For v0 ( max ) = 100 V ⇒ vS ( max ) = 101.4 V
N1 160 N
= ⇒ 1 = 1.58
N 2 101.4 N2
From part (a) PIV = 2vS ( max ) − Vγ = 2 ( 26.4 ) − 0.7
or PIV = 52.1 V or, from part (b) PIV = 2 (101.4 ) − 0.7 or PIV = 202.1 V
2.5
(a)
vs (max) = 12 + 2(0.7) = 13.4 V
13.4
vs ( rms ) = ⇒ vs (rms) = 9.48 V
2
(b)
VM VM
Vr = ⇒C =
2 f RC 2 f Vr R
12
C= ⇒ C = 2222 μ F
2 ( 60 )( 0.3)(150 )
(c)
VM ⎡ 2VM ⎤
id , peak = ⎢1 + π ⎥
R ⎢⎣ Vr ⎥⎦
12 ⎡ 2 (12 ) ⎤
= ⎢1 + π ⎥
150 ⎢ 0.3 ⎥
⎣ ⎦
id , peak = 2.33 A
2.6
(a)
vS ( max ) = 12 + 0.7 = 12.7 V
vS ( max )
vS ( rms ) = ⇒ vS ( rms ) = 8.98 V
2
VM V 12
(b) Vr = ⇒C = M = or C = 4444 μ F
fRC fRVr ( 60 )(150 )( 0.3)

3. VM ⎛ VM ⎞ 12 ⎛ 12 ⎞
(c) For the half-wave rectifier iD , max = ⎜ 1 + 4π
⎜ ⎟= ⎜ 1 + 4π
⎟ 150 ⎜ ⎟ or
R ⎝ 2Vr ⎠ ⎝ 2 ( 0.3) ⎟
⎠
iD , max = 4.58 A
2.8
(a)
vs ( peak ) = 15 + 2 ( 0.7 ) = 16.4 V
16.4
vs ( rms ) = = 11.6 V
2
VM 15
(b) C= = = 2857 μ F
2 f RVr 2 ( 60 )(125 )( 0.35 )
2.9
␯S
26
0.6
Ϫ0.6
Ϫ26
25.4
ϩ
␯O
0
0
Ϫ
␯O
Ϫ25.4
2.10
R
iD
ϩ
␯S ϭ ϩ VB ϭ 12 V
Ϫ
Ϫ
␯S
iD
␻t
x1 x2
vS ( t ) = 24sin ω t
T
1
Now iD ( avg ) = iD ( t ) dt
T∫0
24sin x − 12.7
We have for x1 ≤ ω t ≤ x2 iD =
R
To find x1 and x2, 24sin x1 = 12.7
x1 = 0.558 rad
x2 = π − 0.558 = 2.584 rad
Then

4. x2
1 ⎡ 24sin x − 12.7 ⎤
iD ( avg ) = 2 = ∫⎢ ⎥dx
2π ⎣
x1 R ⎦
1 ⎛ 24 ⎞ 1 ⎛ 12.7 ⎞ x2 6.482 4.095
⎜ ⎟ ( − cos x ) x1 − ⇒ R = 1.19Ω
x2
= ⎜ ⎟ ⋅ xx or 2 = −
2π ⎝ R ⎠ 2π ⎝ R ⎠ 1 R R
x −x 2.584 − 0.558
Fraction of time diode is conducting = 2 1 × 100% = × 100% or Fraction = 32.2%
2π 2π
Power rating
x 2
R 2 ⎡ 24sin x − 12.7 ⎤
T
R 2
∫ iD dt = 2π x∫ ⎢
2
Pavg = R ⋅ irms = ⎥ dx
T 0 1
⎣ R ⎦
x2
1 ⎡( 24 ) sin 2 x − 2 (12.7 )( 24 ) sin x + (12.7 ) ⎤dx
2π R ∫ ⎣
2 2
=
⎦
x1
x
( 24 ) ⎡ −
1 ⎡ 2 x sin 2 x ⎤ 2 x2
⎥ − 2 (12.7 )( 24 )( − cos x ) x1 + (12.7 ) xx1 ⎦
2 x2
= ⎢2 ⎤
2π R ⎣ ⎣ 4 ⎦x 1
For R = 1.19 Ω, then Pavg = 17.9 W
2.11
(a)
15
R= = 150Ω
0.1
vS ( max ) = vo ( max ) + Vγ = 15 + 0.7 or vS ( max ) = 15.7 V
15.7
Then vS ( rms ) = = 11.1 V
2
N1 120 N
Now = ⇒ 1 = 10.8
N 2 11.1 N2
VM VM 15
(b) Vr = ⇒C = = or C = 2083 μ F
2 fRC 2 fRVr 2 ( 60 )(150 )( 0.4 )
(c) PIV = 2vS ( max ) − Vγ = 2 (15.7 ) − 0.7 or PIV = 30.7 V
2.12
␯0
D2
␯i ϩ
Ϫ R2 RL
R1
␯0
␯i ϩ
Ϫ RL
R2
R1
For vi > 0
Vγ = 0
Voltage across RL + R1 = vi
⎛ RL ⎞ 1
Voltage Divider ⇒ v0 = ⎜ ⎟ vi = vi
⎝ RL + R1 ⎠ 2

5. ␯0
20
2.13
For vi > 0, (Vγ = 0 )
R1
␯i ϩ
Ϫ ␯0
R2 RL
a.
⎛ R2 || RL ⎞
v0 = ⎜ ⎟ vi
⎝ R2 || RL + R1 ⎠
R2 || RL = 2.2 || 6.8 = 1.66 kΩ
⎛ 1.66 ⎞
v0 = ⎜ ⎟ vi = 0.43 vi
⎝ 1.66 + 2.2 ⎠
␯0
4.3
v0 ( max )
b. v0 ( rms ) = ⇒ v0 ( rms ) = 3.04 V
2
2.14
3.9
IL = ⇒ I 2 = 0.975 mA
4
20 − 3.9
IR = = 1.3417 mA
12
I Z = 1.3417 − 0.975 ⇒ I Z = 0.367 mA
PT = I Z ⋅ VZ = ( 0.367 )( 3.9 ) ⇒ PT = 1.43 mW
2.15
(a)
40 − 12
IZ = = 0.233 A
120
P = ( 0.233)(12 ) = 2.8 W
(b) IR = 0.233 A, IL = (0.9)(0.233) = 0.21 A
12
So 0.21 = ⇒ RL = 57.1Ω
RL
(c) P = ( 0.1)( 0.233)(12 ) ⇒ P = 0.28 W
2.16
Ri
VI V0
II ϩ
VZ RL
Ϫ
IZ IL
VI = 6.3 V, Ri = 12Ω, VZ = 4.8

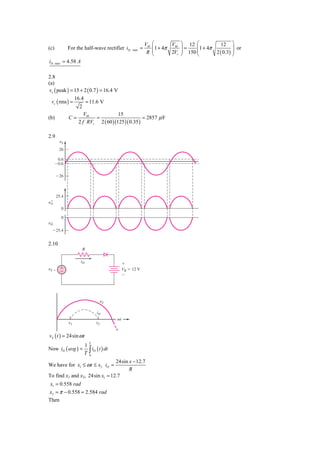
6. a.
6.3 − 4.8
II = ⇒ 125 mA
12
I L = I I − I Z = 125 − I Z
25 ≤ I L ≤ 120 mA ⇒ 40 ≤ RL ≤ 192Ω
b.
PZ = I Z VZ = (100 )( 4.8 ) ⇒ PZ = 480 mW
PL = I LV0 = (120 )( 4.8 ) ⇒ PL = 576 mW
2.17
a.
20 − 10
II = ⇒ I I = 45.0 mA
222
10
IL = ⇒ I L = 26.3 mA
380
I Z = I I − I L ⇒ I Z = 18.7 mA
b.
400
PZ ( max ) = 400 mW ⇒ I Z ( max ) = = 40 mA
10
⇒ I L ( min ) = I I − I Z ( max ) = 45 − 40
10
⇒ I L ( min ) = 5 mA =
RL
⇒ RL = 2 kΩ
(c) For Ri = 175Ω I I = 57.1 mA I L = 26.3 mA I Z = 30.8 mA
I Z ( max ) = 40 mA ⇒ I L ( min ) = 57.1 − 40 = 17.1 mA
10
RL = ⇒ RL = 585Ω
17.1
2.18
a. From Eq. (2-31)
500 [ 20 − 10] − 50 [15 − 10]
I Z ( max ) =
15 − ( 0.9 )(10 ) − ( 0.1)( 20 )
5000 − 250
=
4
I Z ( max ) = 1.1875 A
I Z ( min ) = 0.11875 A
20 − 10
From Eq. (2-29(b)) Ri = ⇒ Ri = 8.08Ω
1187.5 + 50
b.
PZ = (1.1875 )(10 ) ⇒ PZ = 11.9 W
PL = I L ( max ) V0 = ( 0.5 )(10 ) ⇒ PL = 5 W
2.19
(a) As approximation, assume I Z ( max ) and I Z ( min ) are the same as in problem 2.18.
V0 ( max ) = V0 ( nom ) + I Z ( max ) rZ
= 10 + (1.1875)(2) = 12.375 V
V0 ( min ) = V0 ( nom ) + I Z ( min ) rZ
= 10 + (0.11875)(2) = 10.2375 V

7. 12.375 − 10.2375
b. % Reg = × 100% ⇒ % Reg = 21.4%
10
2.20
VL ( max ) − VL ( min )
% Reg = × 100%
VL ( nom )
VL ( nom ) + I Z ( max ) rz − (VL ( nom ) + I Z ( min ) rz )
=
VL ( nom )
⎡ I Z ( max ) − I Z ( min ) ⎤ ( 3)
=⎣ ⎦ = 0.05
6
So I Z ( max ) − I Z ( min ) = 0.1 A
6 6
Now I L ( max ) = = 0.012 A, I L ( min ) = = 0.006 A
500 1000
VPS ( min ) − VZ
Now Ri =
I Z ( min ) + I L ( max )
15 − 6
or 280 = ⇒ I Z ( min ) = 0.020 A
I Z ( min ) + 0.012
VPS ( max ) − VZ
Then I Z ( max ) = 0.1 + 0.02 = 0.12 A and Ri =
I Z ( max ) + I L ( min )
VPS ( max ) − 6
or 280 = ⇒ VPS ( max ) = 41.3 V
0.12 + 0.006
2.21
Using Figure 2.21
a. VPS = 20 ± 25% ⇒ 15 ≤ VPS ≤ 25 V
For VPS ( min ) :
I I = I Z ( min ) + I L ( max ) = 5 + 20 = 25 mA
VPS ( min ) − VZ 15 − 10
Ri = = ⇒ Ri = 200Ω
II 25
25 − 10
b. For VPS ( max ) ⇒ I I ( max ) = ⇒ I I ( max ) = 75 mA
Ri
For I L ( min ) = 0 ⇒ I Z ( max ) = 75 mA
VZ 0 = VZ − I Z rZ = 10 − ( 0.025 )( 5 ) = 9.875 V
V0 ( max ) = 9.875 + ( 0.075 )( 5 ) = 10.25
V0 ( min ) = 9.875 + ( 0.005 )( 5 ) = 9.90
ΔV0 = 0.35 V
ΔV0
c. % Reg = × 100% ⇒ % Reg = 3.5%
V0 ( nom )
2.22
From Equation (2.29(a))
VPS ( min ) − VZ 24 − 16
Ri = = or Ri = 18.2Ω
I Z ( min ) + I L ( max ) 40 + 400
VM VM
Also Vr = ⇒C =
2 fRC 2 fRVr
R ≅ Ri + rz = 18.2 + 2 = 20.2Ω
Then

8. 24
C= ⇒ C = 9901 μ F
2 ( 60 )(1)( 20.2 )
2.23
VZ = VZ 0 + I Z rZ VZ ( nom ) = 8 V
8 = VZ 0 + ( 0.1)( 0.5 ) ⇒ VZ 0 = 7.95 V
VS ( max ) − VZ ( nom ) 12 − 8
Ii = = = 1.333 A
Ri 3
For I L = 0.2 A ⇒ I Z = 1.133 A
For I L = 1 A ⇒ I Z = 0.333 A
VL ( max ) = VZ 0 + I Z ( max ) rZ
= 7.95 + (1.133)( 0.5 ) = 8.5165
VL ( min ) = VZ 0 + I Z ( min ) rZ
= 7.95 + ( 0.333)( 0.5 ) = 8.1165
ΔVL = 0.4 V
ΔVL 0.4
% Reg = = ⇒ % Reg = 5.0%
V0 ( nom ) 8
VM VM
Vr = ⇒C =
2 fRC 2 fRVr
R = Ri + rz = 3 + 0.5 = 3.5Ω
12
Then C = ⇒ C = 0.0357 F
2 ( 60 )( 3.5 )( 0.8 )
2.24
(a) For −10 ≤ vI ≤ 0, both diodes are conducting ⇒ vO = 0
For 0 ≤ vI ≤ 3, Zener not in breakdown, so i1 = 0, vO = 0
vI − 3
For vI > 3 i1 = mA
20
⎛ v −3⎞ 1
vo = ⎜ I ⎟ (10 ) = vI − 1.5
⎝ 20 ⎠ 2
At vI = 10 V, vo = 3.5 V, i1 = 0.35 mA
␯O(V)
4
3.5
Ϫ10 3.0 10 ␯I(V)
(b) For vI < 0, both diodes forward biased
0 − vI
−i1 = . At vI = −10 V , i1 = −1 mA
10
v −3
For vI > 3, i1 = I . At vI = 10 V , i1 = 0.35 mA
20

9. i1(mA)
0.35
Ϫ10 3 10 ␯I(V)
Ϫ1
2.25
(a)
1K
␯I ␯0
1K 2K
ϩ15
V1
1
V1 = × 15 = 5 V ⇒ for vI ≤ 5.7, v0 = vI
3
For vI > 5.7 V
vI − (V1 + 0.7 ) 15 − V1 V1
+ = , v0 = V1 + 0.7
1 2 1
vI − v0 15 − ( v0 − 0.7 ) v0 − 0.7
+ =
1 2 1
vI 15.7 0.7 ⎛ 1 1 1⎞
+ + = v0 ⎜ + + ⎟ = v0 ( 2.5 )
1 2 1 ⎝ 1 2 1⎠
1
vI + 8.55 = v0 ( 2.5 ) ⇒ v0 = vI + 3.42
2.5
vI = 5.7 ⇒ v0 = 5.7
vI = 15 ⇒ v0 = 9.42
␯0(V)
9.42
5.7
0 5.7 15 ␯I (V)
(b) iD = 0 for 0 ≤ vI ≤ 5.7
Then for vI > 5.7 V
⎛ v ⎞
vI − ⎜ I + 3.42 ⎟
vI − vO ⎝ 2.5 ⎠ or i = 0.6vI − 3.42 For v = 15, i = 5.58 mA
iD = = D I D
1 1 1

10. iD(mA)
5.58
5.7 15 ␯I (V)
2.26
⎛ 20 ⎞
(a) For D off, vo = ⎜ ⎟ (20) − 10 = 3.33 V
⎝ 30 ⎠
Then for vI ≤ 3.33 + 0.7 = 4.03 V ⇒ vo = 3.33 V
For vI > 4.03, vo = vl − 0.7;
For vI = 10, vo = 9.3
␯O(V)
9.3
3.33
0 4.03 10 ␯I (V)
(b) For vI ≤ 4.03 V , iD = 0
10 − vo vo − ( −10 )
For vI > 4.03, iD + =
10 20
3
Which yields iD = vI − 0.605
20
For vI = 10, iD = 0.895 mA
iD(mA)
0.895
0 4.03 10 ␯I(V)
2.27
␯O
12.5
10.7
Ϫ30
10.7 30 ␯I
Ϫ30
30 − 10.7
For vI = 30 V, i = = 0.175 A
100 + 10
v0 = i(10) + 10.7 = 12.5 V

11. b.
␯O
12.5
10.7
0
Ϫ30
2.28
ϩ 5Ϫ
␯I ␯O
R ϭ 6.8 K
Vγ = 0.6 V
vI = 15sin ω t
␯O
␯O
Ϫ4.4
Ϫ19.4
2.29
a.
Vγ = 0
0
Ϫ3 V
Vγ = 0.6
0
Ϫ2.4
b.
Vγ = 0
20
5
Vγ = 0.6
19.4
5
2.30

12. 10
6.7
0
Ϫ4.7
Ϫ10
2.31
One possible example is shown.
Ri D L
Ii
ϩ ϩ ϩ
Ϫ VZ ϭ 14 V Ϫ RADIO
DZ Ϫ
Vign VRADIO
L will tend to block the transient signals
Dz will limit the voltage to +14 V and −0.7 V.
Power ratings depends on number of pulses per second and duration of pulse.
2.32
␯O(V)
40
(a) 0
␯O(V)
35
0
(b) Ϫ5
2.33
C
␯I ␯O
ϩ
Vx
Ϫ
a. For Vγ = 0 ⇒ Vx = 2.7 V
b. For Vγ = 0.7 V ⇒ Vx = 2.0 V
2.34
C
ϩ ϩ
␯I Ϫ ␯O
10 V
ϩ
Ϫ Ϫ
2.35

13. 20
␯O
10
0 VB ϭ 0
␯I
Ϫ10
20 ␯O
13
10
3
0 VB ϭ ϩ3 V
Ϫ7 ␯I ϩ VB
20
␯O
10
7
0 VB ϭ Ϫ3 V
Ϫ3
␯ I ϩ VB
Ϫ13
2.36
For Figure P2.32(a)
10
␯I
0
Ϫ10 ␯O
Ϫ20
2.37
a.
10 − 0.6
I D1 = ⇒ I D1 = 0.94 mA ID2 = 0
9.5 + 0.5
V0 = I D1 ( 9.5 ) ⇒ V0 = 8.93 V
b.
5 − 0.6
I D1 = ⇒ I D1 = 0.44 mA ID2 = 0
9.5 + 0.5
V0 = I D1 ( 9.5 ) ⇒ V0 = 4.18 V
c. Same as (a)
d.
(I )
10 = ( 0.5 ) + 0.6 + I ( 9.5 ) ⇒ I = 0.964 mA
2
V0 = I ( 9.5 ) ⇒ V0 = 9.16 V
I
I D1 = I D 2 = ⇒ I D1 = I D 2 = 0.482 mA
2
2.38
a. I = I D1 = I D 2 = 0 V0 = 10
b.

14. 10 = I ( 9.5 ) + 0.6 + I ( 0.5 ) ⇒ I = I D 2 = 0.94 mA I D1 = 0
V0 = 10 − I ( 9.5 ) ⇒ V0 = 1.07 V
c.
10 = I ( 9.5 ) + 0.6 + I ( 0.5 ) + 5 ⇒ I = I D 2 = 0.44 mA I D1 = 0
V0 = 10 − I ( 9.5 ) ⇒ V0 = 5.82 V
d.
I
10 = I ( 9.5 ) + 0.6 + ( 0.5) ⇒ I = 0.964 mA
2
I
I D1 = I D 2 = ⇒ I D1 = I D 2 = 0.482 mA
2
V0 = 10 − I ( 9.5 ) ⇒ V0 = 0.842 V
2.39
a.
V1 = V2 = 0 ⇒ D1 , D2 , D3 , on V0 = 4.4 V
10 − 4.4
I= ⇒ I = 0.589 mA
9.5
4.4 − 0.6
I D1 = ID2 = ⇒ I D1 = I D 2 = 7.6 mA
0.5
I D3 = I D1 + I D 2 − I = 2 ( 7.6 ) − 0.589 ⇒ I D 3 = 14.6 mA
b.
V1 = V2 = 5 V D1 and D2 on, D3 off
I
10 = I ( 9.5 ) + 0.6 + ( 0.5 ) + 5 ⇒ I = 0.451 mA
2
I
I D1 = I D 2 = ⇒ I D1 = I D 2 = 0.226 mA
2
I D3 = 0
V0 = 10 − I ( 9.5 ) = 10 − ( 0.451)( 9.5 ) ⇒ V0 = 5.72 V
c. V1 = 5 V, V2 = 0 D1 off, D2, D3 on V0 = 4.4 V
10 − 4.4
I= ⇒ I = 0.589 mA
9.5
4.4 − 0.6
I D2 = ⇒ I D 2 = 7.6 mA
0.5
I D1 = 0
I D 3 = I D 2 − I = 7.6 − 0.589 ⇒ I D 3 = 7.01 mA
d. V1 = 5 V, V2 = 2 V D1 off, D2, D3 on V0 = 4.4 V
10 − 4.4
I= ⇒ I = 0.589 mA
9.5
4.4 − 0.6 − 2
I D2 = ⇒ I D 2 = 3.6 mA
0.5
I D1 = 0
I D 3 = I D 2 − I = 3.6 − 0.589 ⇒ I D 3 = 3.01 mA
2.40
(a) D1 on, D2 off, D3 on
So I D 2 = 0
10 − 0.6 − ( −0.6 ) 10
Now V2 = −0.6V , I D1 = = ⇒ I D1 = 1.25 mA
R1 + R2 2+6

15. V1 = 10 − 0.6 − (1.25 )( 2 ) ⇒ V1 = 6.9 V
−0.6 − ( −5 )
I R3 = = 2.2 mA
2
I D3 = I R 3 − I D1 = 2.2 − 1.25 ⇒ I D 3 = 0.95 mA
(b) D1 on, D2 on, D3 off
So I D 3 = 0
10 − 0.6 − 4.4 5
V1 = 4.4 V , I D1 = =
R1 6
or I D1 = 0.833 mA
4.4 − ( −5 ) 9.4
I R2 = = = 0.94 mA
R2 + R3 10
I D 2 = I R 2 − I D1 = 0.94 − 0.833 ⇒ I D 2 = 0.107 mA
V2 = I R 2 R3 − 5 = ( 0.94 )( 5 ) − 5 ⇒ V2 = −0.3 V
(c) All diodes are on V1 = 4.4V , V2 = −0.6 V
10 − 0.6 − 4.4
I D1 = 0.5 mA = ⇒ R1 = 10 k Ω
R1
4.4 − ( −0.6 )
I R 2 = 0.5 + 0.5 = 1 mA = ⇒ R2 = 5 k Ω
R2
−0.6 − ( −5 )
I R 3 = 1.5 mA = ⇒ R3 = 2.93 k Ω
R3
2.41
⎛ 0.5 ⎞
For vI small, both diodes off vO = ⎜ ⎟ vI = 0.0909vI
⎝ 0.5 + 5 ⎠
When vI − vO = 0.6, D1 turns on. So we have vI − 0.0909vI = 0.6 ⇒ vI = 0.66, vO = 0.06
vI − 0.6 − vO vI − vO vO 2v − 0.6
For D1 on + = which yields vO = I
5 5 0.5 12
2vI − 0.6
When vO = 0.6, D2 turns on. Then 0.6 = ⇒ vI = 3.9 V
12
v − 0.6 − vO vI − vO vO vO − 0.6
Now for vI > 3.9 I + = +
5 5 0.5 0.5
2vI + 5.4
Which yields vO = ; For vI = 10 ⇒ vO = 1.15 V
22
2.42
ϩ10 V
10 K
D1 D2
␯I ␯0
D3 D4 10 K
10 K
Ϫ10 V

16. For vI > 0. when D1 and D4 turn off
10 − 0.7
I= = 0.465 mA
20
v0 = I (10 kΩ ) = 4.65 V
␯0
4.65
Ϫ10 Ϫ4.65
4.65 10 ␯I
Ϫ4.65
v0 = vI for − 4.65 ≤ vI ≤ 4.65
2.43
a.
R1 D2
ϩ10 V V0
D1
R2
ID1
Ϫ10 V
R1 = 5 kΩ, R2 = 10 kΩ
D1 and D2 on ⇒ V0 = 0
10 − 0.7 0 − ( −10 )
I D1 = − = 1.86 − 1.0
5 10
I D1 = 0.86 mA
b.
R1 = 10 kΩ, R2 = 5 kΩ, D1 off, D2 on I D1 = 0
10 − 0.7 − ( −10 )
I= = 1.287
15
V0 = IR2 − 10 ⇒ V0 = −3.57 V
2.44
If both diodes on
(a)
VA = −0.7 V, VO = −1.4 V
10 − ( −0.7 )
I R1 = = 1.07 mA
10
−1.4 − ( −15 )
IR2 = = 2.72 mA
5
I R1 + I D1 = I R 2 ⇒ I D1 = 2.72 − 1.07
I D1 = 1.65 mA
(b) D1 off, D2 on
10 − 0.7 − ( −15 )
I R1 = I R 2 = = 1.62 mA
5 + 10
VO = I R 2 R2 − 15 = (1.62 )(10 ) − 15 ⇒ VO = 1.2 V
VA = 1.2 + 0.7 = 1.9 V ⇒ D1 off ,
I D1 = 0
2.45

17. (a) D1 on, D2 off
10 − 0.7
I D1 = = 0.93 mA
10
VO = −15 V
(b) D1 on, D2 off
10 − 0.7
I D1 = = 1.86 mA
5
VO = −15 V
2.46
15 − (V0 + 0.7 )
V0 + 0.7 V0
= +
10 20 20
15 0.7 0.7 ⎛ 1 1 1 ⎞ ⎛ 4.0 ⎞
− − = V0 ⎜ + + ⎟ = V0 ⎜ ⎟
10 10 20 ⎝ 10 20 20 ⎠ ⎝ 20 ⎠
V0 = 6.975 V
V0
ID = ⇒ I D = 0.349 mA
20
2.47
10 K Ϫ VD ϩ 10 K
Va Vb
V1 V2
ID
10 K 10 K
a. V1 = 15 V, V2 = 10 V Diode off
Va = 7.5 V, Vb = 5 V ⇒ VD = −2.5 V
ID = 0
b. V1 = 10 V, V2 = 15 V Diode on
V2 − Vb Vb Va Va − V1
= + + ⇒ Va = Vb − 0.6
10 10 10 10
15 10 ⎛1 1⎞ ⎛1 1⎞ ⎛ 1 1⎞
+ = Vb ⎜ + ⎟ + Vb ⎜ + ⎟ − 0.6 ⎜ + ⎟
10 10 ⎝ 10 10 ⎠ ⎝ 10 10 ⎠ ⎝ 10 10 ⎠
⎛ 4⎞
2.62 = Vb ⎜ ⎟ ⇒ Vb = 6.55 V
⎝ 10 ⎠
15 − 6.55 6.55
ID = − ⇒ I D = 0.19 mA
10 10
VD = 0.6 V
2.48 vI = 0, D1 off, D2 on
10 − 2.5
I= = 0.5 mA
15
vo = 10 − ( 0.5 )( 5 ) ⇒ vo = 7.5 V for 0 ≤ vI ≤ 7.5 V
For vI > 7.5 V , Both D1 and D2 on
vI − vo vo − 2.5 vo − 10
= + or vI = vo ( 5.5 ) − 33.75
15 10 5
When vo = 10 V, D2 turns off
vI = (10 )( 5.5 ) − 33.75 = 21.25 V
For vI > 21.25 V, vo = 10 V

18. 2.49
a. V01 = V02 = 0
b. V01 = 4.4 V, V02 = 3.8 V
c. V01 = 4.4 V, V02 = 3.8 V
Logic “1” level degrades as it goes through additional logic gates.
2.50
a. V01 = V02 = 5 V
b. V01 = 0.6 V, V02 = 1.2 V
c. V01 = 0.6 V, V02 = 1.2 V
Logic “0” signal degrades as it goes through additional logic gates.
2.51
(V1 AND V2 ) OR (V3 AND V4 )
2.52
10 − 1.5 − 0.2
I= = 12 mA = 0.012
R + 10
8.3
R + 10 = = 691.7Ω
0.012
R = 681.7Ω
2.53
10 − 1.7 − VI
I= =8
0.75
VI = 10 − 1.7 − 8 ( 0.75 ) ⇒ VI = 2.3 V
2.54
ϩ VR Ϫ
ϩ
VPS Rϭ 2 K
Ϫ
VR = 1 V, I = 0.8 mA
VPS = 1 + ( 0.8 )( 2 )
VPS = 2.6 V
2.55
I Ph = η eΦA
0.6 × 10−3 = (1) (1.6 × 10−19 )(1017 ) A
A = 3.75 × 10−2 cm 2