This document contains solutions to examples from Chapter 12 of an exercise book. It includes 12 examples covering topics like: 1) Calculating voltage gain, input resistance, and output resistance of non-inverting op-amps. 2) Analyzing the bandwidth, voltage gain, and input/output resistances of inverting op-amps. 3) Determining the voltage transfer characteristics, transconductance, and voltage gain of BJT common emitter amplifiers. The examples provide step-by-step workings and calculations to arrive at the key parameters and specifications for different amplifier circuit configurations.

1. Chapter 12
Exercise Solutions
EX12.1
A
a. Af =
1 + Aβ
A A
1 + Aβ = ⇒ Aβ = −1
Af Af
1 1 1 1
β= − = − = 0.05 − 0.0001 ⇒ β = 0.0499
Af A 20 104
Af 20 20
b. = = = 0.998
(1/ β ) (1/ 0.0499 ) 20.040
EX12.2
A
Af =
1 + Aβ
1 1 1 1
β= − = − 6 = 0.01 − 10−6
Af A 100 10
β = 0.009999
dAf 1 dA ⎛ Af ⎞ dA
= ⋅
= ⋅
Af (1 + β A) A ⎜ A ⎟ A
⎝ ⎠
dAf ⎛ 100 ⎞ dAf
= ⎜ 6 ⎟ ( 20 ) % ⇒ = 0.002%
Af ⎝ 10 ⎠ Af
EX12.3
Bandwidth = ω H (1 + β A0 )
⎛A ⎞ ⎛ 105 ⎞
= ω H ⎜ 0 ⎟ = ( 2π )(10 ) ⎜ ⎟
⎝ At ⎠ ⎝ 100 ⎠
ω = ( 2π ) (104 ) rad / sec ⇒ f = 10 kHz
EX12.4
(a)
vOA = A1 A2 vi + A2 vn
= (100 )(10 ) vi + (10 ) vn
So 1000vi S
= = 100 i
No 10vn Ni
(b)
A1 A2 A2
vOC = vi + vn
1 + β Α1 Α2 1 + β Α1 Α2
105 10
= v + vn
1 + ( 0.001)10 1 + ( 0.001) (105 )
5 i
So 103 vi S
= = 104 i
N o 0.1vn Ni

2. EX12.5
a. Vε = VS − V fb = 100 − 99 = 1 m V
5
V0 = AvVε ⇒ Av = ⇒ Av = 5000 V/V
0.001
V fb 0.099
V fb = β V0 ⇒ β = = ⇒ β = 0.0198 V/V
V0 5
Av 5000
Avf = = ⇒ Avf = 50 V/V
1 + β Av 1 + ( 0.0198 )( 5000 )
b. Rif = Ri (1 + β Av ) = ( 5 ) ⎡1 + ( 0.0198 )( 5000 ) ⎤ ⇒ Rif = 500 kΩ
⎣ ⎦
R0 4
R0 f = = ⇒ R0 f ⇒ 40 Ω
1 + β Av 1 + ( 0.0198 )( 5000 )
EX12.6
a. I ε = I S − I fb = 100 − 99 = 1 μ A
I0 5
Ai = = ⇒ Ai = 5000 A/A
I ε 0.001
I fb 0.099
β= = ⇒ β = 0.0198 A/A
I0 5
Ai 5000
Aif = = ⇒ Aif = 50 A/A
1 + Ai β 1 + ( 5000 )( 0.0198 )
Ri 5
b. Rif = = ⇒ Rif ⇒ 50 Ω
1 + β Ai 1 + ( 0.0198 )( 5000 )
R0 f = (1 + β Ai ) R0 = ⎡1 + ( 0.0198 )( 5000 ) ⎤ ( 4 ) ⇒ R0 f = 400 kΩ
⎣ ⎦
EX12.7
Av 104
Avf = = ⇒ Avf = 3.9984
Av 104
1+ 1+
1 + ( R2 / R1 ) 1 + ( 30 /10 )
105
Avf = = 3.99984
105
1+
1 + ( 30 /10 )
3.99984 − 3.9984
× 100% ⇒ 0.0360%
3.9984
EX12.8
Use a non inverting op-amp.
R R
1 + 2 = 15 ⇒ 2 = 14
R1 R1
Let R2 = 140 K
R1 = 10 K
1
β= = 0.066667
R2
1+
R1

3. Input resistance.
Rif = 5 ( 0.06667 ) ( 5 × 103 ) ≅ 1.67 MΩ
50
Rof = ≡ 0.15Ω
( 0.066667 ) ( 5 × 103 )
EX12.9
⎛ ⎞
⎛ h ⎞⎜ RE ⎟
io = ⎜ FE ⎟ ⎜ ⎟ ⋅ ii
⎝ 1 + hFE ⎠ ⎜ R + rk ⎟
⎜ E 1+ h ⎟
⎝ FE ⎠
( 80 )( 0.026 )
rk = = 4.16 k Ω
0.5
Then
rk 4.16
= = 0.0514 k Ω
1 + hFE 81
Then we want
io ⎛ 80 ⎞ ⎛ RE ⎞
= 0.95 = ⎜ ⎟ ⎜ ⎟
ii ⎝ 81 ⎠ ⎝ RE + 0.0514 ⎠
or
⎛ RE ⎞
⎜ ⎟ = 0.9619
⎝ RE + 0.0514 ⎠
which yields
RE ( min ) = 1.30 k Ω
and
⎛ 81 ⎞
V + = I E RE + 0.7 = ⎜ ⎟ ( 0.5 )(1.3) + 0.7 ⇒ V + ( min ) = 1.36 V
⎝ 80 ⎠
EX12.10
Use the configuration shown in figure 12.20.
RS = 500 Ω, RL = 200 Ω
RF
Let 1 + = 15
R1
For example, let R1 = 2 K
RF = 28 K
EX12.11
a.
⎛ R2 ⎞ ⎛ 20 ⎞
VG = ⎜ ⎟ (10 ) − 5 = ⎜ ⎟ (10 ) − 5
⎝ R1 + R2 ⎠ ⎝ 20 + 30 ⎠
VG = −1 V
VS = −1 − VGS
VS − ( −5 )
= K n (VGS − VTN )
2
ID =
RS
( −1) − VGS + 5 = (1.5)( 0.4 )(VGS − 2 )
2

4. 4 − VGS = 0.6 (V 2GS − 4VGS + 4 )
0.6V 2GS − 1.4VGS − 1.6 = 0
(1.4 ) + 4 ( 0.6 )(1.6 )
2
1.4 ±
VGS =
2 ( 0.6 )
VGS = 3.174 V
g m = 2 K n (VGS − VTN ) = 2 (1.5 )( 3.17 − 2 )
g m = 3.52 mA / V
⎛ RD ⎞ ⎛ 2 ⎞
I0 = − ⎜ ⎟ ( g mVgs ) = − ⎜ ⎟ ( 3.52 ) Vgs
⎝ RD + RL ⎠ ⎝ 2+2⎠
I 0 = −1.76Vgs
Vi
Vi = Vgs + g mVgs RS ⇒ Vgs =
1 + g m RS
Vi
Vgs = = ( 0.4153) Vi
1 + ( 3.52 )( 0.4 )
I0
I 0 = − (1.76 )( 0.4153)Vi ⇒ Agf = = −0.731 mA / V
Vi
b. For K n = 1 mA / V 2
From dc analysis:
4 − VGS = (1)( 0.4 )(VGS − 2 )
2
4 − VGS = 0.4 (V 2GS − 4VGS + 4 )
0.4V 2GS − 0.6VGS − 2.4 = 0
( 0.6 ) + 4 ( 0.4 )( 2.4 )
2
0.6 ±
VGS =
2 ( 0.4 )
VGS = 3.31V
g m = 2 (1)( 3.31 − 2 ) = 2.623 mA / V
⎛ 2 ⎞
I0 = − ⎜ ⎟ ( 2.623) Vgs = −1.311Vgs
⎝ 2+2⎠
Vi
Vgs = = Vi ( 0.488 )
1 + ( 2.623)( 0.4 )
I 0 = − (1.31)( 0.488 )Vi

5. I0
Agf = = −0.6398 mA / V
Vi
0.731 − 0.6398
% change = ⇒ 12.5%
0.731
EX12.12
Use the circuit with the configuration shown in Figure 12.27.
The LED replaces RL .
1
Agf = 10 mS = 10 × 10−3 = ⇒ RE = 100 Ω
RE
EX12.13
dc analysis:
10 − V0 V0
= ID + (1)
4.7 47 + 20
I D = K n (VGS − VTN )
2
(2)
⎛ 20 ⎞
VGS = ⎜ ⎟ V0 = 0.2985V0 (3)
⎝ 20 + 47 ⎠
2.13 − V0 ( 0.213) = I D + ( 0.0149 ) V0
(1)
I D = 2.13 − V0 ( 0.2279 )
From (2):
2.13 − V0 ( 0.2279 ) = 1 ⎡( 0.2985V0 ) − 1.5⎤
2
⎣ ⎦
2.13 − V0 ( 0.2279 ) = 0.0891V0 − 0.8955V0 + 2.25
2
0.0891V0 − 0.6676V0 + 0.12 = 0
2
( 0.6676 ) − 4 ( 0.0891)( 0.12 )
2
0.6676 ±
V0 =
2 ( 0.0891)
V0 = 7.31 V
10 − 7.31 7.31
ID = − = 0.572 − 0.109
4.7 67
I D = 0.463 mA
0.463
VGS = + 1.5 = 2.18
1
a. g m = 2 K n (VGS − VTN ) = 2 (1)( 2.18 − 1.5 ) ⇒ g m = 1.36 mA/V

6. V0 V0 − Vgs
+ g mVgs + = 0 (1)
RD RF
Vgs − Vi Vgs − V0
+ =0 (2)
RS RF
⎛ 1 1 ⎞ V0 Vi
Vgs ⎜ + ⎟= +
⎝ RS RF ⎠ RF RS
⎛ 1 1 ⎞ V V
Vgs ⎜ + ⎟ = 0 + i
⎝ 20 47 ⎠ 47 20
Vgs ( 0.0713) = V0 ( 0.0213) + Vi ( 0.050 )
Vgs = V0 ( 0.299 ) + Vi ( 0.701)
From (1):
V0 V Vgs
+ (1.36 ) Vgs + 0 − =0
4.7 47 47
V0 ( 0.213) + (1.36 ) Vgs + V0 ( 0.213) − Vgs ( 0.0213) = 0
V0 ( 0.234 ) + Vgs (1.34 ) = 0
V0 ( 0.234 ) + (1.34 ) ⎡(V0 )( 0.299 ) + (Vi )( 0.701) ⎤ = 0
⎣ ⎦
V0
V0 ( 0.635 ) + Vi ( 0.939 ) = 0 ⇒ Avf = = −1.48
Vi
b. For K n = 1.5 mA / V 2
From dc analysis:
2.13 − V0 ( 0.2279 ) = 1.5 ⎣( 0.2985V0 ) − 1.5⎦
2
⎡ ⎤
= 1.5 ⎡0.0891V0 − 0.8955V0 + 2.25⎤
2
⎣ ⎦
= 0.1337V0 − 1.343V0 + 3.375
2
0.1337V0 − 1.115V0 + 1.245 = 0
2
(1.115) − 4 ( 0.1337 )(1.245 )
2
1.115 ±
V0 =
2 ( 0.1337 )
1.115 ± 0.7597
V0 = ⇒ V0 = 7.01 V
2 ( 0.1337 )
10 − 7.01 7.01
ID = − = 0.636 − 0.105
4.7 67
I D = 0.531 mA
0.531
VGS = + 1.5 = 2.09
1.5
g m = 2 K n (VGS − VTN ) = 2 (1.5 )( 2.09 − 1.5 )
= 1.77 mA/V
From ac analysis:
V0 V Vgs
+ (1.77 )Vgs + 0 − =0
4.7 47 47

7. V0 ( 0.213) + (1.77 ) Vgs + V0 ( 0.0213) − Vgs ( 0.0213) = 0
V0 ( 0.234 ) + Vgs (1.75 ) = 0
V0 ( 0.234 ) + (1.75 ) ⎡V0 ( 0.299 ) + Vi ( 0.701) ⎤ = 0
⎣ ⎦
V0
V0 ( 0.757 ) + Vi (1.23) = 0 ⇒ Avf = = −1.62
Vi
1.62 − 1.48
% change = ⇒ 9.46%
1.48
EX12.14
a. Input resistance.
V0 V0 − Vgs
+ g mVgs + = 0 (1)
RD RF
Vgs − V0
Ii = (2)
RF
So V0 = Vgs − I i RF
⎛ 1 1 ⎞ ⎛ 1 ⎞
V0 ⎜ + ⎟ + Vgs ⎜ g m − ⎟ = 0 (1)
⎝ RD RF ⎠ ⎝ RF ⎠
⎛ 1 1 ⎞ ⎛ 1 ⎞
⎡Vgs − I i ( 47 ) ⎤ ⎜
⎣ ⎦ 4.7 + 47 ⎟ + Vgs ⎜1.36 − 47 ⎟ = 0
⎝ ⎠ ⎝ ⎠
⎡Vgs − I i ( 47 ) ⎤ ( 0.234 ) + Vgs (1.34 ) = 0
⎣ ⎦
Vgs
Vgs (1.57 ) = I i (11.0 ) ⇒ Rif = = 7.0 kΩ
Ii
Output Resistance.

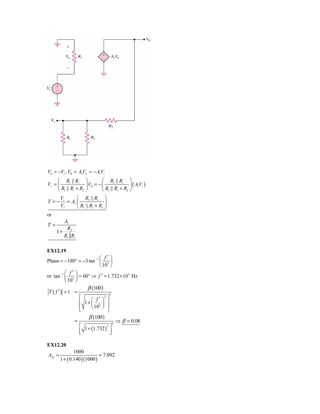
8. VX VX
IX = + g mVgs +
RD RS + RF
⎛ RS ⎞ ⎛ 20 ⎞
Vgs = ⎜ ⎟ VX = ⎜ ⎟ VX = 0.2985VX
⎝ RS + RF ⎠ ⎝ 20 + 47 ⎠
V VX
I X = X + (1.36)(0.2985)VX +
4.7 20 + 47
I X = VX [ 0.213 + 0.406 + 0.0149]
VX
R0 f = = 1.58 kΩ
IX
b. From part (a)
⎛ 1 ⎞
⎡Vgs − I i ( 47 ) ⎤ ( 0.234 ) + Vgs ⎜ 1.77 − ⎟ = 0
⎣ ⎦
⎝ 47 ⎠
Vgs
Vgs (1.98 ) = I i (11) ⇒ Rif = = 5.56 kΩ
Ii
VX VX
IX = + (1.77 )( 0.2985 ) VX +
4.7 20 + 47
VX
I X = VX [ 0.213 + 0.528 + 0.0149] ⇒ R0 f = = 1.32 kΩ
IX
EX12.15
Use the circuit with the configuration shown in Figure 12.41
Let RF = 10 K
EX12.16
⎛ 5.5 ⎞
VTH = ⎜ ⎟ (10 ) = 0.9735 V
⎝ 5.5 + 51 ⎠
RTH = 5.5 || 51 = 4.965 kΩ
0.973 − 0.7
I BQ = = 0.00217 mA
4.96 + (121)(1)
I CQ = 0.2605 mA
rπ = 11.98 kΩ, g m = 10.02 mA / V
Req = RS || R1 || R2 || rπ = (10 ) || 51|| 5.5 || 12
= 2.598 kΩ
From Equation (12.99(b)):
⎛ Req ⎞
T = ( g m RC ) ⎜
⎜R +R +R ⎟ ⎟
⎝ C F eq ⎠
⎛ 2.598 ⎞
= (10 )(10 ) ⎜ ⎟ ⇒ T = 2.75
⎝ 10 + 82 + 2.598 ⎠
EX12.17 Computer Analysis
EX12.18

9. Vε = −Vt , V0 = AvVε = − AvVt
⎛ R1 || Ri ⎞ ⎛ R1 || Ri ⎞
Vr = ⎜ ⎟ V0 = − ⎜ ⎟ ( AvVt )
⎝ R1 || Ri + R2 ⎠ ⎝ R1 || Ri + R2 ⎠
Vr ⎛ R1 || Ri ⎞
T =− = Av ⎜ ⎟
Vt ⎝ R1 || Ri + R2 ⎠
or
Av
T=
R
1+ 2
R1 Ri
EX12.19
⎛ f′ ⎞
Phase = −180° = −3 tan −1 ⎜ 5 ⎟
⎝ 10 ⎠
⎛ f′ ⎞
or tan −1 ⎜ 5 ⎟ = 60° ⇒ f ′ = 1.732 × 105 Hz
⎝ 10 ⎠
β (100 )
T ( f ′) = 1 = 3
⎡ ⎛ f′ ⎞ ⎤
2
⎢ 1+ ⎜ 5 ⎟ ⎥
⎢ ⎝ 10 ⎠ ⎥
⎣ ⎦
β (100 )
= 3
⇒ β = 0.08
⎡ 1 + (1.732 )2 ⎤
⎢
⎣ ⎥
⎦
EX12.20
1000
Afo = = 7.092
1 + ( 0.140 )(1000 )

10. ( 0.140 )(1000 )
T =1=
2 2
⎛ f ⎞ ⎛ f ⎞ ⎛ f ⎞
1 + ⎜ 3 ⎟. 1 + ⎜ 4 ⎟
1+ ⎜ 6 ⎟
⎝ 10 ⎠ ⎝ 5 × 10 ⎠ ⎝ 10 ⎠
By trial and error, at f = 7.65 × 104 Hz
( 0.140 )(1000 )
T =
1 + ( 76.5 ) 1 + (1.53) 1 + ( 0.0765 )
2 2 2
( 0.140 )(1000 )
= = 1.00
( 76.5 )(1.828 )(1.0 )
Then
φ = − ⎡ tan −1 (76.5) + tan −1 (1.53) + tan −1 (0.0765) ⎤
⎣ ⎦
= − [89.25 + 56.83 + 4.37 ] = −150.45
Phase Marge = 180 − 150.45 = 29.5°
EX12.21
The new loop gain function is
105 1
T ′( f ) = ×
⎛ f ⎞⎛ f ⎞ ⎛1 + j ⋅ f ⎞ ⎛1 + j ⋅ f ⎞
⎜1 + j ⋅ ⎟⎜ 1 + j ⋅ ⎟ ⎜ ⎟⎜ ⎟
5 × 108 ⎠
⎝ f PD ⎠ ⎝ 5 × 105 ⎠ ⎝ 107 ⎠ ⎝
⎧
⎪ ⎛ f ⎞ −1 ⎛ f ⎞ ⎛ f ⎞ ⎛ f ⎞⎫ ⎪
Phase = − ⎨ tan −1 ⎜ ⎟ + tan ⎜ 5 ⎟
+ tan −1 ⎜ 7 ⎟ + tan −1 ⎜ 8 ⎟⎬
⎪
⎩ ⎝ f PD ⎠ ⎝ 5 × 10 ⎠ ⎝ 10 ⎠ ⎝ 5 × 10 ⎠ ⎪
⎭
For a phase margin 45° ⇒ Phase = −135°, the poles are far apart so this will occur at approximately
f ′ = 5 × 105 Hz. Then
105
T ′( f ) = 1 =
2
⎛ 5 × 105 ⎞
1+ ⎜ ⎟ × 1+1× 1× 1
⎝ f PD ⎠
105
1=
2
⎛ 5 × 105 ⎞
(1.414 ) 1+ ⎜ ⎟
⎝ f PD ⎠
2
⎛ 5 × 105 ⎞
1+ ⎜ ⎟ = 5 × 10
9
⎝ f PD ⎠
5 × 105
f PD ≅ ⇒ f PD = 7.07 Hz
5 × 109
EX12.22
A0 2 × 105
Af ( 0 ) = = ⇒ Af (0) ≅ 20
1 + β A0 1 + ( 0.05 ) ( 2 × 105 )
f C = f PD (1 + β A0 ) = 100 ⎡1 + ( 0.05 ) ( 2 × 105 ) ⎤ ⇒ fC ≅ 1 MHz
⎣ ⎦
EX12.23
Phase Margin = 45° ⇒ Phase = −135°
This will occur at approximately f ′ = 107 Hz

11. 105
T ′( f ) = 1 =
2
⎛ 107 ⎞
1+ ⎜ ⎟ × 2× 1
⎝ f PD ⎠
2
⎛ 107 ⎞
1+ ⎜ ⎟ = 5 × 10
9
⎝ f PD ⎠
107
f PD ≅ ⇒ f PD = 141 Hz
5 × 109
TYU12.1
A
Af =
1 + Aβ
A f + A f Aβ = A
Af = A (1 − Af β )
Af 80
A= =
1 − Af β 1 − ( 80 )( 0.0120 )
A = 2000
TYU12.2
dAf 1 dA ⎛ Af ⎞ dA
= ⋅ =⎜ ⎟.
Af (1 + β A) A ⎝ A ⎠ A
dA dAf ⎛ A ⎞ ⎛ 5 × 105 ⎞ dA
= ⋅⎜
⎜A ⎟ = ( 0.001) ⎜
⎟ ⎟⇒ = ±5%
A Af ⎝ f ⎠ ⎝ 100 ⎠ A
TYU12.3
Af ⋅ f H = A0 ⋅ f1
A0 ⋅ f1 (10 ) ( 8 )
6
Af = = ⇒ Af ( 0 ) = 32
fH 250 × 103
TYU12.4
Vε = VS − V fb = 100 − 99 = 1 mV
I 0 5 mA
Ag = = ⇒ Ag = 5 A/V
Vε 1 mV
V fb 99 mV
β= = ⇒ β = 19.8 V/A
I0 5 mA
Ag 5
Agf = = ⇒ Agf = 0.05 A/V = 50 mA/V
1 + β Ag 1 + (19.8 )( 5 )
TYU12.5

12. I ε = I S − I fb = 100 − 99 = 1 μ A
V0 5V
Az = = ⇒ Az = 5 × 106 V/A
Iε 1 μ A
I fb 99 μ A
β= = ⇒ β = 1.98 × 10−5 A/V
V0 5V
Az 5 × 106
Azf = = ⇒ Azf = 5 × 104 V/A = 50 V/mA
1 + β Az 1 + (1.98 × 10−5 )( 5 × 106 )
TYU12.6
hFEVT (100 )( 0.026 )
a. rπ = = = 5.2 kΩ
I CQ 0.5
I CQ 0.5
gm = = = 19.23 mA / V
VT 0.026
⎛1 ⎞ ⎛ 1 ⎞
⎜ + g m ⎟ RE ⎜ + 19.23 ⎟ ( 2 )
rπ
Avf = ⎝ ⎠ = ⎝ ⎠
5.2
⎛1 ⎞ ⎛ 1 ⎞
1 + ⎜ + g m ⎟ RE 1 + ⎜ + 19.23 ⎟ ( 2 )
⎝ rπ ⎠ ⎝ 5.2 ⎠
(19.42 )( 2 )
= ⇒ Avf = 0.97490
1 + (19.42 )( 2 )
Rif = rπ + (1 + hFE ) RE = 5.2 + (101)( 2 ) ⇒ Rif = 207.2 kΩ
rπ 5.2
R0 f = RE =2 ⇒ R0 f = 0.0502 kΩ ⇒ 50.2 Ω
1 + hFE 101
b. hFE = 150 ⇒ rπ = 7.8 kΩ, g m = 19.23mA/V
⎛ 1 ⎞
⎜ + 19.23 ⎟ ( 2 )
(19.36 )( 2 )
Avf = ⎝ ⎠
7.8
=
⎛ 1 ⎞ 1 + (19.36 )( 2 )
1+ ⎜ + 19.23 ⎟ ( 2 )
⎝ 7.8 ⎠
Avf = 0.97482 ⇒ 0.0082% change in Avf
Rif = 7.8 + (101)( 2 ) = 209.8 kΩ ⇒ 1.25% change in Rif
rπ 7.8
R0 f = RE =2 = 2 0.0517
1 + hFE 151
R0 f = 50.36 Ω ⇒ 0.319% change in R0 f
TYU12.7

13. V0 = ( g mVgs ) RS
Vi = Vgs + g m RSVgs
Vi
Vgs =
1 + g m RS
g m = 2 K n I DQ = 2 ( 0.2 )( 0.25 ) = 0.447 mA / V
V0 g m RS
Avf = =
Vi 1 + g m RS
( 0.447 )( 5 )
Avf = ⇒ Avf = 0.691
1 + ( 0.447 )( 5 )
Rif = ∞
VX
I X = g mVgs =
RS
Vgs = −VX
⎛ 1 ⎞
I X = VX ⎜ g m + ⎟
⎝ RS ⎠
1 1
R0 f = RS = 5
gm 0.447
R0 f = 1.55 kΩ
TYU12.8 Computer Analysis
TYU12.9 Computer Analysis
TYU12.10
hFE ⋅ Ag ( 200 ) (103 )
a. Agf = = ⇒ Agf = 10−3 A/V=1 mA/V
1 + ( hFE Ag ) RE 1 + ( 200 ) (103 )(103 )
( 200 ) (104 )
b. Agf = ⇒ Agf ≅ 1 mA/V
1 + ( 200 ) (104 )(103 )

14. Percent change is negligible. ( 4.5 × 10−7 % )
( 200 ) (104 ) ( 200 ) (103 )
−
1 + ( 200 ) (104 )(103 ) 1 + ( 200 ) (103 )(103 )
10−3
( 200 ) (104 ) ⎡1 + ( 200 ) (104 )(103 )⎤
⎣ ⎦
=
(10 )( 2 ×10 )( 2 ×10 )
−3 9 8
(200)(103 )[1 + (200)(104 )(103 )]
−
(10−3 )(2 × 109 )(2 × 108 )
200 × 104 − 200 × 103
= = 4.5 × 10−9
(10−3 )( 2 ×109 )( 2 ×108 )
TYU12.11
T = Ai β =
Ai 0 β
=
(10 ) ( 0.01)
5
⎛ f ⎞ ⎛ f ⎞
⎜ 1 + j ⋅ ⎟ 1 + j ⋅ ⎜ 10 ⎟
⎝ f1 ⎠ ⎝ ⎠
3
10
T ( f1 ) =1=
⎛ f′⎞
2
1+ ⎜ E ⎟
⎝ 10 ⎠
⎛ f′⎞
2
1 + ⎜ E ⎟ = 106
⎝ 10 ⎠
f E′ = 10 106 − 1 ⇒ f E′ ≈ 104 Hz
⎛ f′⎞ ⎛ 104 ⎞
Phase = φ = − tan −1 ⎜ E ⎟ = − tan −1 ⎜ ⎟
⎝ 10 ⎠ ⎝ 10 ⎠
= − tan −1 (103 )
φ ≈ 90°
Phase Margin = 180 − 90 ⇒ Phase Margin = 90°
TYU12.12
Αι 0 β
T = Ai β =
⎛ f ⎞⎛ f ⎞
⎜ 1+ j ⋅ ⎟ ⎜1 + j ⋅ ⎟
⎝ f1 ⎠ ⎝ f2 ⎠
⎡ ⎛ f ⎞ ⎛ f ⎞⎤
Phase = − ⎢ tan −1 ⎜ ⎟ + tan −1 ⎜ ⎟ ⎥
⎣ ⎝ f1 ⎠ ⎝ f2 ⎠⎦
Phase Margin = 60° ⇒ Phase = −120°
⎡ ⎛ f ⎞ ⎛ f ⎞⎤
−120° = − ⎢ tan −1 ⎜ 4 ⎟ + tan −1 ⎜ 5 ⎟ ⎥
⎣ ⎝ 10 ⎠ ⎝ 10 ⎠ ⎦
At f ′ = 7.66 × 104 Hz,
Phase = − ⎡ tan −1 ( 7.66 ) + tan −1 ( 0.766 ) ⎤
⎣ ⎦
= − [82.56 + 37.45]
= −120°

15. T ( f ′) = 1 =
(10 ) β
5
1+ ( 7.66 ) × 1 + ( 0.766 )
2 2
1=
(10 ) β
5
⇒ β = 9.73× 10−5
( 7.725 )(1.26 )
TYU12.13
Phase Margin = 60° ⇒ Phase = −120°
⎛ f′ ⎞
Phase = −120° = −3 tan −1 ⎜ 5 ⎟
⎝ 10 ⎠
⎛ f′ ⎞
tan −1 ⎜ 5 ⎟ = 40° ⇒ f ′ = 0.839 × 105 Hz
⎝ 10 ⎠
β (100 )
T ( f ′) = 1 = 3
⎡ ⎛ f′ ⎞ ⎤
2
⎢ 1+ ⎜ 5 ⎟ ⎥
⎢ ⎝ 10 ⎠ ⎥
⎣ ⎦
β (100 )
= 3
⇒ β = 0.0222
⎡ 1 + ( 0.839 )2 ⎤
⎢
⎣ ⎥
⎦