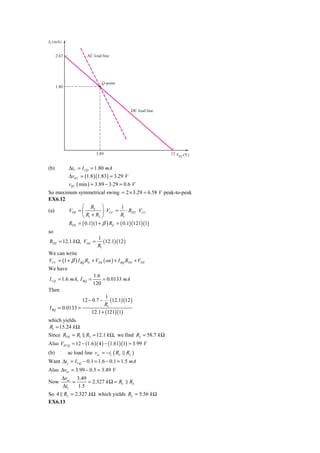
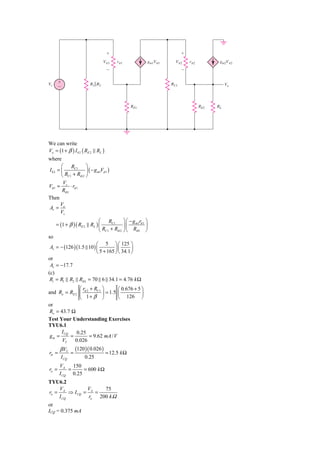
1) The document contains example problems from Chapter 6 of a textbook on exercise problems involving BJT circuit analysis. 2) Problem EX6.1 involves calculating currents, voltages, and gain for a common-emitter amplifier. 3) Problem EX6.12 involves calculating the bias resistor values needed to produce a specified quiescent current and voltage for a common-emitter amplifier.

1. Chapter 6
Exercise Problems
EX6.1
VBB − VBE ( on ) 2 − 0.7
(a) I BQ = = ⇒ 2 μA
RB 650
Then
I CQ = β I BQ = (100 )( 2 μ A ) = 0.20 mA
VCEQ = VCC − I CQ RC = 5 − ( 0.2 )(15 ) = 2 V
(b) Now
I CQ 0.20
gm = = = 7.69 mA / V
VT 0.026
and
β VT (100 )( 0.026 )
rπ = = = 13 k Ω
I CQ 0.20
(c)
We find
⎛ r ⎞
Av = − g m RC ⎜ π ⎟
⎝ rπ + RB ⎠
⎛ 13 ⎞
= − ( 7.69 )(15 ) ⎜ ⎟ = −2.26
⎝ 13 + 650 ⎠
EX6.2
V − VBE ( on ) 0.92 − 0.7
I BQ = BB =
RB 100
or I BQ = 0.0022 mA
and I CQ = β I BQ = (150 )( 0.0022 ) = 0.33 mA
(a)
I CQ 0.33
gm = = = 12.7 mA / V
VT 0.026
β VT (150 )( 0.026 )
rπ = = = 11.8 k Ω
I CQ 0.33
VA 200
ro = = = 606 k Ω
I CQ 0.33
(b)
⎛ rπ ⎞
vo = − g m vπ ( ro RC ) and vπ = ⎜ ⎟ ⋅ vs
⎝ rπ + RB ⎠
so
vo ⎛ rπ ⎞
Av = = − gm ⎜ ⎟ ( ro RC )
vπ ⎝ rπ + RB ⎠
⎛ 11.8 ⎞
= − (12.7 ) ⎜ ⎟ ( 606 15 )
⎝ 11.8 + 100 ⎠
which yields Av = −19.6
EX6.3
(a)
V − VEB ( on ) 1.145 − 0.7
I BQ = BB =
RB 50
or I BQ = 0.0089 mA
Then I CQ = β I BQ = ( 90 )( 0.0089 ) = 0.801 mA

2. Now
I CQ 0.801
gm = = = 30.8 mA / V
VT 0.026
β VT ( 90 )( 0.026 )
rπ = = = 2.92 k Ω
I CQ 0.801
VA 120
ro = = = 150 k Ω
I CQ 0.801
(b) We have Vo = g mVπ ( ro RC )
⎛ r ⎞
and Vπ = − ⎜ π ⎟ Vs
⎝ rπ + RB ⎠
so
V ⎛ rπ ⎞
Av = o = − g m ⎜ ⎟ ( ro RC )
Vs ⎝ rπ + RB ⎠
⎛ 2.92 ⎞
= − ( 30.8 ) ⎜ ⎟ (150 2.5 )
⎝ 2.92 + 50 ⎠
which yields Av = −4.18
EX6.4
Using Figure 6.23
(a) For I CQ = 0.2 mA, 7.8 < hie < 15 k Ω, 60 < h fe < 125, 6.2 × 10−4 < hre < 50 × 10−4 ,
5 < hoe < 13 μ mhos
(b) For I CQ = 5 mA, 0.7 < hie < 1.1 k Ω, 140 < h fe < 210, 1.05 × 10−4 < hre < 1.6 ×10−4 ,
22 < hoe < 35 μ mhos
EX6.5
RTH = R1 R2 = 35.2 || 5.83 = 5 k Ω
⎛ R2 ⎞ ⎛ 5.83 ⎞
VTH = ⎜ ⎟ ⋅ VCC = ⎜ ⎟ (5)
⎝ R1 + R2 ⎠ ⎝ 5.83 + 35.2 ⎠
or
VTH = 0.7105 V
Then
V − VBE ( on ) 0.7105 − 0.7
I BQ = TH =
RTH 5
or
I BQ = 2.1 μ A
and
I CQ = β I BQ = (100 )( 2.1 μ A ) = 0.21 mA
VCEQ = VCC − I CQ RC = 5 − ( 0.21)(10 )
and
VCEQ = 2.9 V
Now
I CQ 0.21
gm = = = 8.08 mA
VT 0.026
VA 100
ro = = = 476 k Ω
I CQ 0.21
And
Av = − g m ( ro RC ) = − ( 8.08 ) ( 476 10 )
so
Av = −79.1
EX6.6

3. RTH = R1 R2 = 250 75 = 57.7 k Ω
⎛ R2 ⎞ ⎛ 75 ⎞
VTH = ⎜ ⎟ (VCC ) = ⎜ ⎟ (5)
⎝ R1 + R2 ⎠ ⎝ 75 + 250 ⎠
or
VTH = 1.154 V
VTH − VBE ( on ) 1.154 − 0.7
I BQ = =
RTH + (1 + β ) RE 57.7 + (121)( 0.6 )
or
I BQ = 3.48 μ A
I CQ = β I BQ = (120 )( 3.38 μ A ) = 0.418 mA
(a)
Now
I CQ 0.418
gm = = = 16.08 mA / V
VT 0.026
βVT (120 )( 0.026 )
rπ = = = 7.46 k Ω
I CQ 0.418
We have
Vo = − g mVπ RC
We find
Rib = rπ + (1 + β ) RE = 7.46 + (121)( 0.6 )
or
Rib = 80.1 k Ω
Also
R1 R2 = 250 75 = 57.7 k Ω
R1 R2 Rib = 57.7 80.1 = 33.54 k Ω
We find
⎛ R1 R2 Rib ⎞ ⎛ 33.54 ⎞
Vs′ = ⎜ ⎟ ⋅ Vs = ⎜ ⎟ ⋅ Vs
⎝ R1 R2 Rib + RS ⎠ ⎝ 33.54 + 0.5 ⎠
or
Vs′ = ( 0.985 ) Vs
Now
⎡ ⎛1+ β ⎞ ⎤ ⎡ ⎛ 121 ⎞ ⎤
Vs′ = Vπ ⎢1 + ⎜ ⎟ RE ⎥ = Vπ ⎢1 + ⎜ ⎟ ( 0.6 ) ⎥
⎢ ⎝
⎣ rπ ⎠ ⎥ ⎦ ⎣ ⎝ 7.46 ⎠ ⎦
or
Vπ = ( 0.0932 ) Vs′ = ( 0.0932 )( 0.985 ) Vs
So
Vo
Av = = − (16.08 )( 0.0932 )( 0.985 )( 5.6 )
Vs
or
Av = −8.27
EX6.7
RTH = R1 R2 = 15 85 = 12.75 k Ω
⎛ R2 ⎞ ⎛ 85 ⎞
VTH = ⎜ ⎟ ⋅ VCC = ⎜ ⎟ (12 )
⎝ R1 + R2 ⎠ ⎝ 15 + 85 ⎠
or
VTH = 10.2 V
Now
VCC = (1 + β ) I BQ RE + VEB ( on ) + I BQ RTH + VTH

4. so
12 = (101) I BQ ( 0.5 ) + 0.7 + I BQ (12.75 ) + 10.2
which yields
I BQ = 0.0174 mA
and
I CQ = β I BQ = (100 )( 0.0174 ) = 1.74 mA
I EQ = (101)( 0.0174 ) = 1.76 mA
VECQ = VCC − I EQ RE − I CQ RC
= 12 − (1.76 )( 0.5 ) − (1.74 )( 4 )
or
VECQ = 4.16 V
Now
β VT (100 )( 0.026 )
rπ = = = 1.49 k Ω
I CQ 1.74
We have
Vo = g mVπ ( RC || RL )
⎛ V ⎞
Vs = −Vπ − ⎜ g mVπ + π ⎟ RE
⎝ rπ ⎠
Solving for Vπ and noting that β = g m rπ , we find
Vo − β ( RC RL )
Av = =
Vs rπ + (1 + β ) RE
− (100 )( 4 2 )
=
1.49 + (101)( 0.5 )
or Av = −2.56
EX6.8
Dc analysis
10 − 0.7
I BQ = = 0.00439 mA
100 + (101)( 20 )
I CQ = 0.439 mA, I EQ = 0.443 mA
Now
(100 )( 0.026 )
rπ = = 5.92 k Ω
0.439
0.439
gm = = 16.88 mA / V
0.026
100
ro = = 228 k Ω
0.439
(a)
Now
Vo = − g mVπ ( ro RC )
⎛ RB rπ ⎞
Vπ = ⎜ ⎟ ⋅ Vs
⎝ RB rπ + RS ⎠
RB rπ = 100 5.92 = 5.59 k Ω
⎛ 5.59 ⎞
Then Vπ = ⎜ ⎟ ⋅ Vs = ( 0.918 ) Vs
⎝ 5.59 + 0.5 ⎠
V
Then Av = o = − (16.88 ) ( 0.918 ) ( 228 10 )
Vs
or Av = −148
(b) Rin = RS + RB rπ = 0.5 + 100 5.92 = 6.09 k Ω

5. and
Ro = RC ro = 10 228 = 9.58 k Ω
EX6.9
(a)
I CQ 0.25
gm = = = 9.615 mA / V
VT 0.026
VA 100
ro = = = 400 k Ω
I CQ 0.25
Av = − g m ( ro rc ) = − ( 9.615 )( 400 100 ) = −769
(b)
Av = − g m ( ro rc rL ) = − ( 9.615 )( 400 100 100 )
Av = −427
EX6.10
5 − 0.7
I BQ = = 0.00672 mA
10 + (126 )( 5 )
I CQ = 0.84 mA, I EQ = 0.847 mA
VCEQ = 10 − ( 0.84 )( 2.3) − ( 0.847 )( 5 )
or
VCEQ = 3.83 V
dc load line
VCE ≅ (V + − V − ) − I C ( RC + RE )
or
VCE = 10 − I C ( 7.3)
ac load line (neglecting ro)
vce = −ic ( RC RL ) = −ic ( 2.3 5 ) = −ic (1.58 )
IC (mA)
1.37 AC load line
Q-point
0.84
DC load line
3.83 10 V
CE (V)
EX6.11
(a)
dc load line
VEC ≅ VCC − I C ( RC + RE ) = 12 − I C ( 4.5 )
ac load line
vec ≅ −ic ( RE + RC RL ) or vec = −ic ( 0.5 + 4 2 ) = −ic (1.83)
Q-point values
12 − 0.7 − 10.2
I BQ = = 0.0150 mA
12.75 + (121)( 0.5 )
I CQ = 1.80 mA, I EQ = 1.82 mA
VECQ = 3.89 V

6. IC (mA)
2.67 AC load line
Q-point
1.80
DC load line
3.89 12 V (V)
EC
(b) ΔiC = I CQ = 1.80 mA
ΔvEC = (1.8 )(1.83) = 3.29 V
vEC ( min ) = 3.89 − 3.29 = 0.6 V
So maximum symmetrical swing = 2 × 3.29 = 6.58 V peak-to-peak
EX6.12
⎛ R2 ⎞ 1
(a) VTH = ⎜ ⎟ ⋅ VCC = ⋅ RTH ⋅ VCC
⎝ R1 + R2 ⎠ R1
RTH = ( 0.1)(1 + β ) RE = ( 0.1)(121)(1)
so
1
RTH = 12.1 k Ω, VTH = (12.1)(12 )
R1
We can write
VCC = (1 + β ) I BQ RE + VEB ( on ) + I BQ RTH + VTH
We have
1.6
I CQ = 1.6 mA, I BQ = = 0.0133 mA
120
Then
1
12 − 0.7 − (12.1)(12 )
R1
I BQ = 0.0133 =
12.1 + (121)(1)
which yields
R1 = 15.24 k Ω
Since RTH = R1 R2 = 12.1 k Ω, we find R2 = 58.7 k Ω
Also VECQ = 12 − (1.6 )( 4 ) − (1.61)(1) = 3.99 V
(b) ac load line vec = −ic ( RC RL )
Want Δic = I CQ − 0.1 = 1.6 − 0.1 = 1.5 mA
Also Δvec = 3.99 − 0.5 = 3.49 V
Δvec 3.49
Now = = 2.327 k Ω = RC RL
Δic 1.5
So 4 RL = 2.327 k Ω which yields RL = 5.56 k Ω
EX6.13

7. RTH = R1 R2 = 25 50 = 16.7 k Ω
⎛ R2 ⎞ ⎛ 50 ⎞
VTH = ⎜ ⎟ ⋅ VCC = ⎜ ⎟ (5)
⎝ R1 + R2 ⎠ ⎝ 25 + 50 ⎠
or
VTH = 3.33 V
VTH − VBE ( on ) 3.33 − 0.7
I BQ = =
RTH + (1 + β ) RE 16.7 + (121)(1)
or
I BQ = 0.0191 mA
Also
I CQ = (120 )( 0.0191) = 2.29 mA
Now
I CQ 2.29
gm = = = 88.1 mA / V
VT 0.026
β VT (120 )( 0.026 )
rπ = = = 1.36 k Ω
I CQ 2.29
VA 100
ro = = = 43.7 k Ω
I CQ 2.29
(a)
⎛ R1 R2 Rib ⎞
Vs′ = ⎜ ⎟ ⋅ Vs
⎝ R1 R2 Rib + RS ⎠
Rib = rπ + (1 + β ) ( RE ro ) = 1.36 + (121)(1 43.7 )
or
Rib = 120 k Ω and R1 R2 = 16.7 k Ω
Then
R1 R2 Rib = 16.7 120 = 14.7 k Ω
Now
⎛ 14.7 ⎞
Vs′ = ⎜ ⎟ ⋅ Vs = ( 0.967 ) Vs
⎝ 14.7 + 0.5 ⎠
and
⎛V ⎞ ⎛ 1+ β ⎞
Vo = ⎜ π + g mVπ ⎟ ( RE ro ) = Vπ ⎜ ⎟ RE ro
⎝ rπ ⎠ ⎝ rπ ⎠
We have
Vs′ = Vπ + Vo
then
Vs′ ( 0.967 )Vs
Vπ = =
⎛ 1+ β ⎞ ⎛1+ β ⎞
1+ ⎜ ⎟ RE ro 1 + ⎜ ⎟ RE ro
⎝ rπ ⎠ ⎝ rπ ⎠
We then obtain
⎛1+ β ⎞
( 0.967 ) ⎜ ⎟ RE ro
V ⎝ rπ ⎠
Av = o =
Vs ⎛1+ β ⎞
1+ ⎜ ⎟ RE ro
⎝ rπ ⎠
( 0.967 )(1 + β ) RE ro
=
rπ + (1 + β ) RE ro
Now
RE ro = 1 43.7 = 0.978 k Ω

8. Then
( 0.967 )(121)( 0.978 )
Av = = 0.956
1.36 + (121)( 0.978 )
(b)
Rib = rπ + (1 + β )( RE ro )
or
Rib = 1.36 + (121)( 0.978 ) = 120 k Ω
EX6.14
For RS = 0, then
r
Ro = RE ro π
1+ β
Using the parameters from Exercise 4.13, we obtain
1.36
Ro = 1 43.7
121
or
Ro = 11.1 Ω
EX6.15
(a) For I CQ = 1.25 mA and β = 100, we find
I EQ = 1.26 mA and I BQ = 0.0125 mA
Now VCEQ = 10 − I EQ RE
Or
4 = 10 − (1.26 ) RE
which yields
RE = 4.76 k Ω
Then
RTH = ( 0.1)(1 + β ) RE = ( 0.1)(101)( 4.76 )
or
RTH = 48.1 k Ω
We have
⎛ R2 ⎞ 1
VTH = ⎜ ⎟ (10 ) − 5 = ⋅ RTH (10 ) − 5
⎝ R1 + R2 ⎠ R1
or
1
VTH = ( 481) − 5
R1
VTH − 0.7 − ( −5 )
We can write I BQ =
RTH + (1 + β ) RE
Or
1
( 481) − 5 − 0.7 + 5
R1
0.0125 =
48.1 + (101)( 4.76 )
which yields
R1 = 65.8 k Ω
Since R1 R2 = 48.1 k Ω, we obtain
R2 = 178.8 k Ω
(b)

9. β VT (100 )( 0.026 )
rπ = = = 2.08 k Ω
I CQ 1.25
VA 125
ro = = = 100 k Ω
I CQ 1.25
We may note that
g mVπ = g m ( I b rπ ) = β I b
Also
Rib = rπ + (1 + β )( RE RL ro )
= 2.08 + (101) ( 4.76 1 100 )
or
Rib = 84.9 k Ω
Now
⎛ RE ro ⎞
⎜ R r + R ⎟(
Io = ⎜ 1 + β ) Ib
⎟
⎝ E o L ⎠
where
⎛ R1 R2 ⎞
Ib = ⎜ ⋅I
⎜R R +R ⎟ s ⎟
⎝ 1 2 ib ⎠
We can then write
I ⎛ RE ro ⎞ ⎛ R1 R2 ⎞
AI = o = ⎜ ⎟ (1 + β ) ⎜ ⎟
I s ⎜ RE ro + RL ⎟
⎝ ⎠
⎜R R +R
⎝ 1 2 ib
⎟
⎠
We have
RE ro = 4.76 100 = 4.54 k Ω
so
⎛ 4.54 ⎞ ⎛ 48.1 ⎞
AI = ⎜ ⎟ (101) ⎜ ⎟
⎝ 4.54 + 1 ⎠ ⎝ 48.1 + 84.9 ⎠
or
AI = 29.9
r 2.08
(c) Ro = RE ro π = 4.76 100
1+ β 101
or Ro = 20.5 Ω
EX6.16
(a)
RTH = R1 R2 = 70 6 = 5.53 k Ω
⎛ R2 ⎞ ⎛ 6 ⎞
VTH = ⎜ ⎟ (10 ) − 5 = ⎜ ⎟ (10 ) − 5
⎝ R1 + R2 ⎠ ⎝ 70 + 6 ⎠
or
VTH = −4.2105 V
We find
−4.2105 − 0.7 − ( −5 )
I BQ1 = ⇒ 2.91 μ A
5.53 + (126 )( 0.2 )
and
I CQ1 = β I BQ1 = (125 )( 2.91 μ A ) = 0.364 mA
I EQ1 = (1 + β ) I BQ1 = 0.368 mA
At the collector of Q1,
5 − VC1 V − 0.7 − ( −5 )
= I CQ1 + C1
RC1 (1 + β )( RE 2 )
or

10. 5 − VC1 V − 0.7 − ( −5 )
= 0.364 + C1
5 (126 )(1.5)
which yields
VC1 = 2.99 V
also
VE1 = I EQ1 RE1 − 5 = ( 0.368 )( 0.2 ) − 5
or
VE1 = −4.93 V
Then
VCEQ1 = VC1 − VE1 = 2.99 − ( −4.93) = 7.92 V
We find
V − 0.7 − ( −5 )
I EQ 2 = C1 = 4.86 mA
1.5
and
⎛ β ⎞ ⎛ 125 ⎞
I CQ 2 = ⎜ ⎟ ⋅ I EQ1 = ⎜ ⎟ ( 4.86 ) = 4.82 mA
⎝ 1+ β ⎠ ⎝ 126 ⎠
We find
VE 2 = VC1 − 0.7 = 2.99 − 0.7 = 2.29 V
and
VCEQ 2 = 5 − VE 2 = 5 − 2.29 = 2.71 V
(b)
The small-signal transistor parameters are:
β VT (125 )( 0.026 )
rπ 1 = = = 8.93 k Ω
I CQ1 0.364
I CQ1 0.364
g m1 = = = 14.0 mA / V
VT 0.026
β VT (125 )( 0.026 )
rπ 2 = = = 0.674 k Ω
I CQ 2 4.82
I CQ 2 4.82
gm2 = = = 185 mA / V
VT 0.026
We find Rib1 = rπ 1 + (1 + β ) RE1 = 8.93 + (126 )( 0.2 )
Or
Rib1 = 34.1 k Ω
and
Rib 2 = rπ 2 + (1 + β )( RE 2 RL )
= 0.674 + (126 )(1.5 10 ) = 165 k Ω
The small-signal equivalent circuit is:

11. ϩ ϩ
V␲1 r␲1 gm1V␲1 V␲2 r␲2 gm2V␲2
Ϫ Ϫ
Vs ϩ R1͉͉R2 RC1 Vo
Ϫ
RE1 RE2 RL
We can write
Vo = (1 + β ) I b 2 ( RE 2 RL )
where
⎛ RC1 ⎞
Ib2 = ⎜ ⎟ ( − g m1Vπ 1 )
⎝ RC1 + Rib 2 ⎠
V
Vπ 1 = s ⋅ rπ 1
Rib1
Then
V
Av = o
Vs
⎛ RC1 ⎞ ⎛ − g m1rπ 1 ⎞
= (1 + β )( RE 2 RL ) ⎜ ⎟⎜ ⎟
⎝ RC1 + Rib 2 ⎠ ⎝ Rib1 ⎠
so
⎛ 5 ⎞ ⎛ 125 ⎞
Av = − (126 )(1.5 10 ) ⎜ ⎟⎜ ⎟
⎝ 5 + 165 ⎠ ⎝ 34.1 ⎠
or
Av = −17.7
(c)
Ri = R1 R2 Rib1 = 70 6 34.1 = 4.76 k Ω
⎛ r + RC1 ⎞ ⎛ 0.676 + 5 ⎞
and Ro = RE 2 ⎜ π 2 ⎟ = 1.5 ⎜ ⎟
⎝ 1+ β ⎠ ⎝ 126 ⎠
or
Ro = 43.7 Ω
Test Your Understanding Exercises
TYU6.1
I CQ 0.25
gm = = = 9.62 mA / V
VT 0.026
β VT (120 )( 0.026 )
rπ = = = 12.5 k Ω
I CQ 0.25
VA 150
ro = = = 600 k Ω
I CQ 0.25
TYU6.2
V V 75
ro = A ⇒ I CQ = A =
I CQ ro 200 k Ω
or
ICQ = 0.375 mA

12. TYU6.3
RC
As a first approximation, Av ≅ −
RE
Resulting gain is always smaller than this value. The effect of RS is very small.
Set
RC
= 10
RE
Now
5 ≅ I C ( RC + RE ) + VCEQ
or
5 = ( 0.5 )( RC + RE ) + 2.5
which yields
RC + RE = 5 k Ω
So
10 RE + RE = 5
or
RE = 0.454 k Ω and RC = 4.54 k Ω
We have
I CQ 0.5
I BQ = = = 0.005 mA
β 100
and
RTH = ( 0.1)(1 + β ) RE = ( 0.1)(101)( 0.454 )
or
RTH = 4.59 k Ω
also
⎛ R2 ⎞ 1
VTH = ⎜ ⎟ ⋅ VCC = ⋅ RTH ⋅ VCC
⎝ R1 + R2 ⎠ R1
or
1 23
VTH = ( 4.59 )( 5 ) =
R1 R1
We can write
VTH = I BQ RTH + VBE ( on ) + (1 + β ) I BQ RE
or
23
= ( 0.005 )( 4.59 ) + 0.7 + (101)( 0.005 )( 0.454 )
R1
which yields
R1 = 24.1 k Ω
and since R1 R2 = 4.59 k Ω
we find R2 = 5.67 k Ω
TYU6.4
dc analysis
RTH = R1 R2 = 15 85 = 12.75 k Ω
⎛ R2 ⎞ ⎛ 85 ⎞
VTH = ⎜ ⎟ ⋅ VCC = ⎜ ⎟ (12 )
⎝ R1 + R2 ⎠ ⎝ 15 + 85 ⎠
or
VTH = 10.2 V
We can write
12 − 0.7 − VTH 12 − 0.7 − 10.2
I BQ = =
RTH + (1 + β ) RE 12.75 + (101)( 0.5 )
or
IBQ = 0.0174 mA

13. and
I CQ = β I BQ = 1.74 mA
ac analysis
Vo = h fe I b ( RC RL )
and
−Vs
Ib =
hie + (1 + h fe ) RE
so
Vo −h fe ( RC RL )
Av = =
Vs hie + (1 + h fe ) RE
For ICQ = 1.74 mA, we find
h fe ( max ) = 110, h fe ( min ) = 70
hie ( max ) = 2 k Ω, hie ( min ) = 1.1 k Ω
We obtain
−110 ( 4 2 )
Av ( max ) = = −2.59
1.1 + (111)( 0.5 )
and
−70 ( 4 2 )
Av ( min ) = = −2.49
2 + ( 71)( 0.5 )
TYU6.5
RC
First approximation, Av ≅ −
RE
RC
This predicts a low value, so set =9
RE
Now
VCC ≅ I CQ ( RC + RE ) + VECQ
or
7.5 = ( 0.6 )( 9 RE + RE ) + 3.75
which yields
RE = 0.625 k Ω and RC = 5.62 k Ω
We have
RTH = ( 0.1)(1 + β ) RE = ( 0.1)(101)( 0.625 )
or
RTH = 6.31 k Ω
Also
1 1
VTH = ⋅ RTH ⋅ VCC = ( 6.31)( 7.5 )
R1 R1
We have
I CQ 0.6
I BQ = = = 0.006 mA
β 100
The KVL equation around the E-B loop gives
VCC = (1 + β ) I BQ RE + VEB ( on ) + I BQ RTH + VTH
or
1
7.5 = (101)( 0.006 )( 0.625 ) + 0.7 + ( 0.006 )( 6.31) + ( 6.31)( 7.5)
R1
which yields
R1 = 7.41 k Ω
Since RTH = R1 R2 = 6.31 k Ω, then R2 = 42.5 k Ω
TYU6.6

14. − β RC ⎛R ⎞
We have Av = = − ( 0.95 ) ⎜ C ⎟
rπ + (1 + β ) RE ⎝ RE ⎠
⎛ 2 ⎞
or Av = − ( 0.95 ) ⎜ ⎟ = −4.75
⎝ 0.4 ⎠
Assume rπ = 1.2 k Ω from Example 4.6.
Then
−β ( 2)
= −4.75
1.2 + (1 + β )( 0.4 )
or
β = 76
TYU6.7
dc analysis: By symmetry, VTH = 0
RTH = R1 R2 = 20 20 = 10 k Ω
We can write
0 − 0.7 − ( −5 )
I BQ = = 0.00672 mA
10 + (126 )( 5 )
I CQ = β I BQ = (125 )( 0.00672 ) = 0.84 mA
Small-signal transistor parameters:
β VT (125 )( 0.026 )
rπ = = = 3.87 k Ω
I CQ 0.84
I CQ 0.84
gm = = = 32.3 mA / V
VT 0.026
VA 200
ro = = = 238 k Ω
I CQ 0.84
(a)
We have
Vo = − g mVπ ( ro RC RL ) and Vπ = Vs
so
Vo
Av = = − g m ( ro RC RL )
Vs
= − ( 32.3)( 238 2.3 5 )
or
Av = −50.5
(b)
Ro = ro RC = 238 2.3 = 2.28 k Ω
TYU6.8
We find I CQ = 0.418 mA, then
⎛ 121 ⎞
VCEQ = 5 − ( 0.418 )( 5.6 ) − ⎜ ⎟ ( 0.418 )( 0.6 )
⎝ 120 ⎠
or
VCEQ = 2.41 V
So
ΔvCE = ( 2.41 − 0.5 ) × 2
or
ΔvCE = 3.82 V peak-to-peak
TYU6.9
dc load line
VCE ≅ (10 + 10 ) − I CQ ( RC + RE )
or

15. VCE = 20 − I C (10 + RE )
ac load line
vce = −ic RC = −ic (10 )
Now
ΔvCE = VCEQ − 0.7 = ΔiC (10 ) = I CQ (10 )
so
VCEQ − 0.7 = I CQ (10 )
We have that
VCEQ = 20 − I CQ (10 + RE )
then
I CQ (10 ) + 0.7 = 20 − I CQ (10 + RE )
or
I CQ ( 20 + RE ) = 19.3 (1)
The base current is found from
10 − 0.7
I BQ =
100 + (101) RE
so
(100 )( 9.3)
I CQ =
100 + (101) RE
Substituting into Equation (1),
⎡ (100 )( 9.3) ⎤
⎢ ⎥ ( 20 + RE ) = 19.3
⎢100 + (101) RE ⎥
⎣ ⎦
which yields
RE = 16.35 k Ω
Then
(100 )( 9.3)
I CQ = = 0.531 mA
100 + (101)(16.35 )
and
VCEQ ≅ 20 − ( 0.531)(10 + 16.35 ) = 6.0 V
Now
ΔvCE = VCEQ − 0.7 = 6 − 0.7 = 5.3 V
or, maximum symmetrical swing = 2 × 5.3 = 10.6 V peak-to-peak
TYU6.10
We can write
0 − 0.7 − ( −10 )
I BQ = ⇒ 6.60 μ A
100 + (131)(10 )
and
I CQ = (130 )( 6.60 μ A ) = 0.857 mA
Assume nominal small-signal parameters of:
hie = 4 k Ω, h fe = 134
1
hre = 0, hoe = 12 μ S ⇒ = 83.3 k Ω
hoe
We find
⎛ 1 ⎞
Rib = hie + (1 + h fe ) ⎜ RE RL ⎟
⎝ hoe ⎠
= 4 + (135 )(10 ||10 || 83.3) = 641 k Ω
To find the voltage gain:

16. RB Rib 100 641
Vs′ = ⋅ Vs = ⋅ Vs
RB Rib + RS 100 641 + 10
or
Vs′ = ( 0.896 ) Vs
Also
Vo
=
(1 + h fe ) R′
Vs′ hie + (1 + h fe ) R′
where
1
R ′ = RE RL = 10 10 83.3 = 4.72 k Ω
hoe
Then
Vo ( 0.896 )(135 )( 4.72 )
Av = = = 0.891
Vs 4 + (135 )( 4.72 )
To find the current gain:
⎛ 1 ⎞
⎜ RE ⎟
Io ⎜ hoe ⎟ ⎛ RB ⎞
⎟(
Ai = = 1 + h fe ) ⎜ ⎟
Ii ⎜ 1 ⎝ RB + Rib ⎠
⎜ RE
⎜ + RL ⎟⎟
⎝ hoe ⎠
⎛ 10 83.3 ⎞ ⎛ 100 ⎞
=⎜ (135 ) ⎜ ⎟
⎝ 10 83.3 + 10 ⎟ ⎠ ⎝ 100 + 641 ⎠
or
Ai = 8.59
To find the output resistance:
1 hie + RS RB
Ro = RE
hoe 1 + h fe
4 + 10 100
= 10 83.3 ⇒ 96.0 Ω
135
TYU6.11
We find
RTH = R1 R2 = 50 50 = 25 k Ω
⎛ R2 ⎞ ⎛1⎞
VTH = ⎜ ⎟ ⋅ VCC = ⎜ ⎟ ( 5 ) = 2.5 V
⎝ R1 + R2 ⎠ ⎝ 2⎠
Now
V − VEB ( on ) − VTH
I BQ = CC
RTH + (1 + β ) RE
5 − 0.7 − 2.5
= = 0.00793 mA
25 + (101)( 2 )
and
I CQ = (100 )( 0.00793) = 0.793 mA
The small-signal transistor parameters:
I CQ 0.793
gm = = = 30.5 mA / V
VT 0.026
β VT (100 )( 0.026 )
rπ = = = 3.28 k Ω
I CQ 0.793
VA 125
ro = = = 158 k Ω
I CQ 0.793
(a)

17. Define R ′ = RE RL ro = 2 0.5 158 ≅ 0.40 k Ω
Now
(1 + β ) R′ (101)( 0.4 )
Av = =
rπ + (1 + β ) R ′ 3.28 + (101)( 0.4 )
or
Av = 0.925
(b)
Rib = rπ + (1 + β ) R ′ = 3.28 + (101)( 0.4 )
or
Rib = 43.7 k Ω
rπ 3.28
Also Ro = RE ro = 2 158
1+ β 101
or Ro = 32.0 Ω
TYU6.12
VCC − VECQ 5 − 2.5
For VECQ = 2.5, I EQ = = = 5 mA
RE 0.5
then
⎛ 75 ⎞
I CQ = ⎜ ⎟ ( 5 ) = 4.93 mA
⎝ 76 ⎠
5
I BQ = = 0.0658 mA
76
Small-signal transistor parmaters:
β VT ( 75 )( 0.026 )
rπ = = = 0.396 k Ω
I CQ 4.93
VA 75
ro = = = 15.2 k Ω
I CQ 4.93
Define the small-signal base current into the base, then
g mVπ = − β I b
Now,
⎛ RE ro ⎞
Io = ⎜ ⎟ (1 + β ) I b
⎝ RE ro + RL ⎠
and
⎛ R1 R2 ⎞
Ib = ⎜ ⎟ ⋅ Ii
⎝ R1 R2 + Rib ⎠
The current gain is
I ⎛ RE ro ⎞ ⎛ R1 R2 ⎞
AI = o = ⎜ ⎟ (1 + β ) ⎜ ⎟
I i ⎝ RE ro + RL ⎠ ⎝ R1 R2 + Rib ⎠
We have
RE = RL = 0.5 k Ω
Rib = rπ + (1 + β )( RE RL ro )
= 0.396 + ( 76 )( 0.5 0.5 15.2 ) = 19.1 k Ω
and
RE ro = 0.5 15.2 = 0.484 k Ω
Then
⎛ 0.484 ⎞ ⎛ R1 R2 ⎞
AI = 10 = ⎜ ⎟ ( 76 ) ⎜ ⎟
⎝ 0.484 + 0.5 ⎠ ⎝ R1 R2 + 19.1 ⎠
which yields
R1 R2 = 6.975 k Ω
Now

18. ⎛ R2 ⎞ 1
VTH = ⎜ ⎟ ⋅ VCC = ⋅ RTH ⋅ VCC
⎝ R1 + R2 ⎠ R1
or
1
VTH = ( 6.975 )( 5 )
R1
We can write
V − VEB ( on ) − VTH
I BQ = CC
RTH + (1 + β ) RE
or
5 − 0.7 − VTH
0.0658 =
6.975 + ( 76 )( 0.5 )
which yields
1
VTH = 1.34 = ( 6.975)( 5 )
R1
or
R1 = 26.0 k Ω and R2 = 9.53 k Ω
TYU6.13
(a)
dc analysis:
V − VEB ( on ) 10 − 0.7
I EQ = EE = = 0.93 mA
RE 10
⎛ β ⎞ ⎛ 100 ⎞
I CQ = ⎜ ⎟ I EQ = ⎜ ⎟ ( 0.93) = 0.921 mA
⎝ 1+ β ⎠ ⎝ 101 ⎠
VECQ = VEE − I EQ RE − I CQ RC − ( −VCC )
= 10 − ( 0.93)(10 ) − ( 0.921)( 5 ) − ( −10 )
or
VECQ = 6.1 V
(b)
Small-signal transistor parameters:
β VT (100 )( 0.026 )
rπ = = = 2.82 k Ω
I CQ 0.921
I CQ 0.921
gm = = = 35.42 mA / V
VT 0.026
Small-signal current gain:
I o = g mVπ and Vπ = Vs
also
Vs ⎛ 1 ⎞
Ii = + g mVπ = Vs ⎜
⎜ R r + gm ⎟ ⎟
RE rπ ⎝ E π ⎠
Then
I g mVπ g m ( RE rπ )
AI = o = =
Ii ⎛ 1 ⎞ 1 + g m ( RE rπ )
Vπ ⎜ + gm ⎟
⎝ RE rπ ⎠
( 35.42 ) (10 2.82 )
=
1 + ( 35.42 ) (10 2.82 )
or
AI = 0.987
(c)
Small-signal voltage gain:

19. Vo = g mVπ RC = g mVs RC
or
V
Av = o = g m RC = ( 35.42 )( 5 )
Vs
or
Av = 177
TYU6.14
(a)
V − VBE ( on ) 10 − 0.7
I BQ = EE =
RB + (1 + β ) RE 100 + (101)(10 )
or
I BQ = 8.38 μ A and I CQ = 0.838 mA
β VT (100 )( 0.026 )
rπ = = = 3.10 k Ω
I CQ 0.838
I CQ 0.838
gm = = = 32.23 mA / V
VT 0.026
VA ∞
ro = = =∞
I CQ 0.838
(b)
Summing currents, we have
V ⎛ −V ⎞ ⎛ −V − Vs ⎞
g mVπ + π = ⎜ π ⎟ + ⎜ π ⎟
rπ ⎝ RE ⎠ ⎝ RS ⎠
or
⎡⎛ 1 + β ⎞ 1 1 ⎤ V
Vπ ⎢⎜ ⎟+ + ⎥=− s
⎢⎝
⎣ rπ ⎠ RE RS ⎥ ⎦ RS
We can then write
V ⎡⎛ r ⎞ ⎤
Vπ = − s ⎢⎜ π ⎟ RE RS ⎥
RS ⎣⎝ 1 + β ⎠ ⎦
Now
Vo = − g mVπ ( RC RL )
So
Av =
Vo
= gm
( RC RL ) ⎡⎛ rπ ⎞ R R ⎤
⎢⎜ ⎟ E S⎥
Vs RS ⎣⎝ 1 + β ⎠ ⎦
( 32.23) (10 1) ⎡ 3.10 ⎤
= ⎢ 101 10 1⎥
(1) ⎣ ⎦
or
Av = 0.870
Now
⎛ RE ⎞ ⎛ 10 ⎞
Ie = ⎜ ⎟ ⋅ Ii = ⎜ ⎟ ⋅ I i = ( 0.763) I i
⎝ RE + rπ ⎠ ⎝ 10 + 3.10 ⎠
⎛ β ⎞ ⎛ 100 ⎞
Ic = ⎜ ⎟ ⋅ Ie = ⎜ ⎟ ⋅ Ie
⎝ 1+ β ⎠ ⎝ 101 ⎠
⎛ RC ⎞ ⎛ 10 ⎞
Io = ⎜ ⎟ ⋅ Ic = ⎜ ⎟ ⋅ I c = ( 0.909 ) I c
⎝ RC + RL ⎠ ⎝ 10 + 1 ⎠
So we have
I ⎛ 100 ⎞
AI = o = ( 0.909 ) ⎜ ⎟ ( 0.763)
Ii ⎝ 101 ⎠

20. or
AI = 0.687
(c)
We have
r 3.10
Ri = RE π = 10
1+ β 101
or
Ri = 30.6 Ω
Also
Ro = RC = 10 k Ω
TYU6.15
dc analysis:
We can write 5 = I BQ RB + VBE ( on ) + I EQ RE
or
5 − 0.7 4.3
I BQ = =
RB + (101) RE RB + (101) RE
(100 )( 4.3)
I CQ =
RB + (101) RE
Also
5 = I CQ RC + VCEQ + I EQ RE − 5
or
⎡ ⎛ 101 ⎞ ⎤
VCEQ = 10 − I CQ ⎢ RC + ⎜ ⎟ RE ⎥
⎣ ⎝ 100 ⎠ ⎦
ac analysis:
Vo = − g mVπ ( RC RL )
and
Vπ ⎛ RB ⎞
Vs = −Vπ − ⋅ RB = −Vπ ⎜1 + ⎟
rπ ⎝ rπ ⎠
or
⎛ r ⎞
Vπ = − ⎜ π ⎟ ⋅ Vs
⎝ rπ + RB ⎠
Then
V β
Av = o =
Vs rπ + RB
( RC RL )
where β = g m rπ
β VT (100 )( 0.026 )
For I CQ = 1 mA, rπ = = = 2.6 k Ω
I CQ 1
Now
(100 ) ( 2 2 )
Av = 20 =
2.6 + RB
which yields
RB = 2.4 k Ω
Also
(100 )( 4.3)
I CQ = 1 =
2.4 + (101) RE
which yields
RE = 4.23 k Ω
TYU6.16
(a)

21. dc analysis:
For I EQ 2 = 1 mA,
⎛ 100 ⎞
I CQ 2 = ⎜ ⎟ (1) = 0.990 mA
⎝ 101 ⎠
I EQ 2 1
I EQ1 = = = 0.0099 mA
1 + β 101
and
I EQ1 0.0099
I BQ1 = = = 0.000098 mA
1+ β 101
and
I CQ1 = (100 )( 0.000098 ) = 0.0098 mA
and
VB1 = − I BQ1 RB = − ( 0.000098 )(10 )
or
VB1 = −0.00098 ≅ 0
so
VE1 = −0.7 V
and
VE 2 = −1.4 V
Now
I1 = I CQ1 + I CQ 2 = 0.0098 + 0.990 ≅ 1 mA
then
VO = 5 − (1)( 4 ) = 1 V
and
VCEQ 2 = 1 − ( −1.4 ) = 2.4 V
VCEQ1 = 1 − ( −0.7 ) = 1.7 V
(b)
Small-signal transistor parameters:
β VT (100 )( 0.026 )
rπ 1 = = = 265 k Ω
I CQ1 0.0098
I CQ1 0.0098
g m1 = = = 0.377 mA
VT 0.026
β VT (100 )( 0.026 )
rπ 2 = = = 2.63 k Ω
I CQ 2 0.990
I CQ 2 0.990
gm2 = = = 38.1 mA / V
VT 0.026
ro1 = ro 2 = ∞
(c)
Small-signal voltage gain: From Figure 4.73 (b)
Vo = − ( g m1Vπ 1 + g m 2Vπ 2 ) RC
Vs = Vπ 1 + Vπ 2
and
⎛V ⎞ ⎛1+ β ⎞
Vπ 2 = ⎜ π 1 + g m1Vπ 1 ⎟ ⋅ rπ 2 = ⎜ ⎟ ⋅ Vπ 1rπ 2
⎝ rπ 1 ⎠ ⎝ rπ 1 ⎠
Then
⎡ ⎛1+ β ⎞ ⎤
Vo = − ⎢ g m1Vπ 1 + g m 2 ⎜ ⎟ ⋅ rπ 2Vπ 1 ⎥ ⋅ RC
⎣ ⎝ rπ 1 ⎠ ⎦
Also

22. ⎛1+ β ⎞
Vs = Vπ 1 + ⎜ ⎟ ⋅ rπ 2Vπ 1
⎝ rπ 1 ⎠
⎡ ⎛ r ⎞⎤
= Vπ 1 ⎢1 + (1 + β ) ⎜ π 2 ⎟ ⎥
⎣ ⎝ rπ 1 ⎠ ⎦
or
Vs
Vπ 1 =
⎛r ⎞
1 + (1 + β ) ⎜ π 2 ⎟
⎝ rπ 1 ⎠
Now
⎡ ⎛ rπ 2 ⎞ ⎤
⎢ g m1 + g m 2 (1 + β ) ⎜ ⎟ ⎥ ⋅ RC
⎝ rπ 1 ⎠ ⎦
Av = o = − ⎣
V
Vs ⎛r ⎞
1 + (1 + β ) ⎜ π 2 ⎟
⎝ rπ 1 ⎠
so
⎡ ⎛ 2.63 ⎞ ⎤
⎢ 0.377 + ( 38.1)(101) ⎜ 265 ⎟ ⎥ ( 4 )
⎝ ⎠⎦
Av = − ⎣
⎛ 2.63 ⎞
1 + (101) ⎜ ⎟
⎝ 265 ⎠
or
Av = −77.0
(d)
Ri = rπ 1 + (1 + β ) rπ 2 = 265 + (101)( 2.63)
or
Ri = 531 k Ω
TYU6.17
(a)
dc analysis:
For R1 + R2 + R3 = 100 k Ω
VCC 12
I1 = = = 0.12 mA
R1 + R2 + R3 100
Now
VE1 = I CQ 2 RE = ( 0.5 )( 0.5 ) = 0.25 V
VC1 = VE1 + VCEQ1 = 0.25 + 4 = 4.25 V
and
VC 2 = VC1 + VCEQ 2 = 4.25 + 4 = 8.25 V
VCC − VC 2 12 − 8.25
So RC = = = 7.5 k Ω
I CQ 0.5
Also
VB1 = VE1 + VBE ( on ) = 0.25 + 0.7 = 0.95 V
And
⎛ R3 ⎞ R3
VB1 = ⎜ ⎟ ⋅ VCC ⇒ 0.95 = (12 )
⎝ R1 + R2 + R3 ⎠ 100
which yields
R3 = 7.92 k Ω
We have
VB 2 = VC1 + VBE ( on ) = 4.25 + 0.7 = 4.95 V
and

23. ⎛ R2 + R3 ⎞
VB 2 = ⎜ ⎟ ⋅ VCC
⎝ R1 + R2 + R3 ⎠
or
⎛ R + 7.92 ⎞
4.95 = ⎜ 2 ⎟ (12 )
⎝ 100 ⎠
which yields
R2 = 33.3 k Ω
Then
R1 = 100 − 33.3 − 7.92 = 58.8 k Ω
(b)
Small-signal transistor parameters:
βV (100 )( 0.026 )
rπ 1 = rπ 2 = T =
I CQ 0.5
or
rπ 1 = rπ 2 = 5.2 k Ω
and
I CQ 0.5
g m1 = g m 2 = =
VT 0.026
or
g m1 = g m 2 = 19.23 mA/V
and
ro1 = ro 2 = ∞
(c)
Small-signal voltage gain:
We have
Vo = − g m 2Vπ 2 ( RC RL )
Also
Vπ 2
+ g m 2Vπ 2 = g m1Vπ 1
rπ 2
or
⎛ r ⎞
Vπ 2 = g m1Vπ 1 ⎜ π 2 ⎟ and Vπ 1 = Vs
⎝ 1+ β ⎠
We find
V ⎛ r ⎞
Av = o = − g m 2 ( RC RL ) g m1 ⎜ π 2 ⎟
Vs ⎝1+ β ⎠
⎛ β ⎞
= − g m 2 ( RC RL ) ⎜ ⎟
⎝ 1+ β ⎠
We obtain
⎛ 100 ⎞
Av = − (19.23) ( 7.5 2 ) ⎜ ⎟
⎝ 101 ⎠
or
Av = −30.1
TYU6.18
(a)
dc analysis: with vs = 0
RTH = R1 R2 = 125 30 = 24.2 k Ω
⎛ R2 ⎞ ⎛ 30 ⎞
VTH = ⎜ ⎟ ⋅ VCC = ⎜ ⎟ (12 )
⎝ R1 + R2 ⎠ ⎝ 125 + 30 ⎠
or
VTH = 2.32 V

24. Now
VTH = I BQ RTH + VBE ( on ) + (1 + β ) I BQ RE
or
2.32 − 0.7
I BQ = = 0.0250 mA
24.2 + ( 81)( 0.5 )
and
I CQ = ( 80 )( 0.025 ) = 2.00 mA
Also
⎡ ⎛1+ β ⎞ ⎤
VCEQ = VCC − I CQ ⎢ RC + ⎜ ⎟ RE ⎥
⎣ ⎝ β ⎠ ⎦
⎡ ⎛ 81 ⎞ ⎤
= 12 − ( 2 ) ⎢ 2 + ⎜ ⎟ ( 0.5 ) ⎥
⎣ ⎝ 80 ⎠ ⎦
or
VCEQ = 6.99 V
Power dissipated in RC:
PRC = I CQ RC = ( 2.0 ) ( 2 ) = 8.0 mW
2 2
Power dissipated in RL:
I LQ = 0 ⇒ PRL = 0
Power dissipated in transistor:
PQ = I BQVBEQ + I CQVCEQ
= ( 0.025 )( 0.7 ) + ( 2.0 )( 6.99 ) = 14.0 mW
(b)
With vs = 18cos ω t ( mV )
β VT (80 )( 0.026 )
rπ = = = 1.04 k Ω
I CQ 2.0
We can write
β
vce =
rπ
( RC RL )VP cos ω t
Power dissipated in RL:
vce ( rms )
2 2
1 1 ⎡β ⎤
pRL = = ⋅ ⋅ ⎢ ( RC RL ) VP ⎥
RL 2 RL ⎣ rπ ⎦
2
⎡ 80
( 2 2 ) ( 0.018)⎤
1 1
= ⋅ ⋅⎢ ⎥
2 2 × 103 ⎣1.04 ⎦
or
pRL = 0.479 mW
Power dissipated in RC:
Since RC = RL = 2 k Ω, we have pRC = 8.0 + 0.479 = 8.48 mW
Power dissipated in transistor: From the text, we have
2
⎛β ⎞ ⎛V ⎞
2
pQ ≅ I CQVCEQ − ⎜ ⎟ ⎜ P ⎟ ( RC RL )
⎝ rπ ⎠ ⎝ 2 ⎠
2 2
⎛ ⎞ ⎛ 0.018 ⎞
= ( 2 × 10−3 ) ( 6.99 ) − ⎜ ⎟ ( 2 × 10 2 × )
80 3 3
3 ⎟ ⎜
⎝ 1.04 × 10 ⎠ ⎝ 2 ⎠
or
pQ = 13.0 mW
TYU6.19
(a)
dc analysis:

25. RTH = R1 R2 = 53.8 10 = 8.43 k Ω
⎛ R2 ⎞ ⎛ 10 ⎞
VTH = ⎜ ⎟ ⋅ VCC = ⎜ ⎟ (5)
⎝ R1 + R2 ⎠ ⎝ 53.8 + 10 ⎠
or
VTH = 0.7837 V
Now
0.7837 − 0.7
I BQ = = 0.00993 mA
8.43
and
I CQ = (100 )( 0.00993) = 0.993 mA
We have
VCEQ = VCC − I CQ RC
or
2.5 = 5 − ( 0.993) RC
which yields
RC = 2.52 k Ω
(b)
Power dissipated in RC:
PRC = I CQ RC = ( 0.993) ( 2.52 )
2 2
or
PRC = 2.48 mW
Power dissipated in transistor:
PQ ≅ I CQVCEQ = ( 0.993)( 2.5 )
or
PQ = 2.48 mW
(c)
ac analysis:
Maximum ac collector current:
ic = ( 0.993) cos ω t ( mA )
average ac power dissipated in RC:
1 1
pRC = ( 0.993) RC = ( 0.993) ( 2.52 )
2 2
2 2
or
pRC = 1.24 mW
Now
pRC 1.24
Fraction = = = 0.25
PRC + PQ 2.48 + 2.48