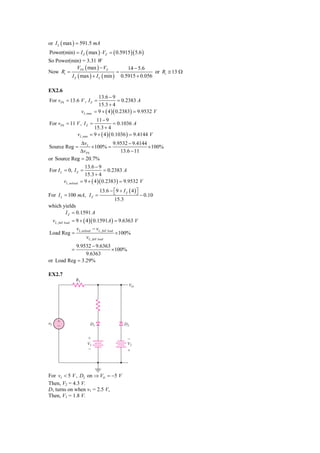
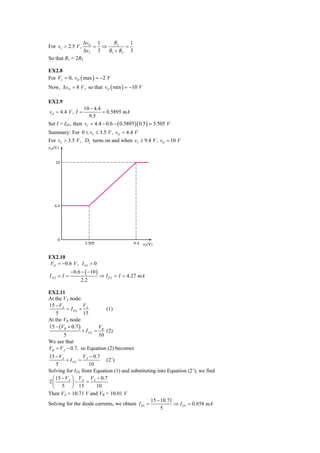
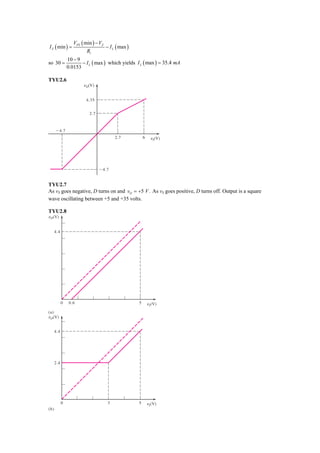
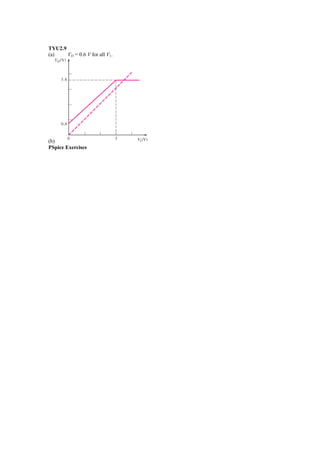
This document contains the solutions to various exercises related to circuit analysis and electronics. Exercise problems cover topics such as diode circuits, rectifiers, filters, and transistor circuits. The solutions involve calculating voltages, currents, power, capacitance values, and other circuit parameters through applying circuit laws and relationships. PSpice simulations are also used to verify some of the circuit responses.

1. Chapter 2
Exercise Problems
EX2.1
30 − 12 − 0.6
iD ( peak ) = = 87 mA
0.2
vR ( max ) = 30 + 12 = 42 V
⎛ 12.6 ⎞
ω t1 = sin −1 ⎜ ⎟ ⇒ 24.8°
⎝ 30 ⎠
By symmetry
ω t2 = 180 − 24.8 = 155.2°
155.2 − 24.8
% time = × 100% = 36.2%
360
EX2.2
(a) vO = 12sin θ1 − 1.4 = 0
1.4
or sin θ1 = = 0.1166
12
which yields
θ1 = 6.7°
By symmetry, θ 2 = 180 − 6.7 = 173.3°
173.3 − 6.7
Then % time = × 100% = 46.3%
360
1.4
(b) sinθ1 = = 0.35
4
which yields
θ1 = 20.5°
By symmetry, θ 2 = 180 − 20.5 = 159.5°
159.5 − 20.5
Then % time = × 100% = 38.6%
360
EX2.3
VM 24
C= = ⇒ or C = 500 μ F
2 fRVr 2 ( 60 ) (103 ) ( 0.4 )
EX2.4
VM VM 75
Vr = ⇒R= or R =
f RC f CVr ( 60 ) ( 50 × 10−6 ) ( 4 )
Then R = 6.25 k Ω
EX2.5
10 ≤ VPS ≤ 14 V , VZ = 5.6 V , 20 ≤ RL ≤ 100 Ω
5.6
I L ( max ) = = 0.28 A,
20
5.6
I L ( min ) = = 0.056 A
100
⎡VPS ( max ) − VZ ⎤ ⋅ I L ( max ) ⎡VPS ( min ) − VZ ⎤ ⋅ I L ( min )
I Z (max) = ⎣ ⎦ − ⎣ ⎦
VPS ( min ) − 0.9VZ − 0.1VPS ( max ) VPS ( min ) − 0.9VZ − 0.1VPS ( max )
(14 − 5.6 )( 280 ) − (10 − 5.6 )( 56 )
or I L ( max ) =
10 − ( 0.9 )( 5.6 ) − ( 0.1)(14 )

2. or I L ( max ) = 591.5 mA
Power(min) = I Z ( max ) ⋅ VZ = ( 0.5915)( 5.6 )
So Power(min) = 3.31 W
VPS ( max ) − VZ 14 − 5.6
Now Ri = = or Ri ≅ 13 Ω
I Z ( max ) + I L ( min ) 0.5915 + 0.056
EX2.6
13.6 − 9
For vPS = 13.6 V , I Z = = 0.2383 A
15.3 + 4
vL ,max = 9 + ( 4 )( 0.2383) = 9.9532 V
11 − 9
For vPS = 11 V , I Z = = 0.1036 A
15.3 + 4
vL ,min = 9 + ( 4 )( 0.1036 ) = 9.4144 V
ΔvL 9.9532 − 9.4144
Source Reg = × 100% = × 100%
ΔvPS 13.6 − 11
or Source Reg = 20.7%
13.6 − 9
For I L = 0, I Z = = 0.2383 A
15.3 + 4
vL , noload = 9 + ( 4 )( 0.2383) = 9.9532 V
13.6 − ⎡9 + I Z ( 4 ) ⎤
⎣ ⎦
For I L = 100 mA, I Z = − 0.10
15.3
which yields
I Z = 0.1591 A
vL , full load = 9 + ( 4 )( 0.1591A ) = 9.6363 V
vL , noload − vL , full load
Load Reg = × 100%
vL , full load
9.9532 − 9.6363
= × 100%
9.6363
or Load Reg = 3.29%
EX2.7
R1
VO
␯I ϩ
Ϫ D1 D2
ϩ Ϫ
V1 V2
Ϫ ϩ
For vI < 5 V , D2 on ⇒ VO = −5 V
Then, V2 = 4.3 V.
D1 turns on when v1 = 2.5 V,
Then, V1 = 1.8 V.

3. ΔvO 1 R2 1
For vI > 2.5 V , = ⇒ =
ΔvI 3 R1 + R2 3
So that R1 = 2R2
EX2.8
For Vγ = 0, vO ( max ) = −2 V
Now, ΔvO = 8 V , so that vO ( min ) = −10 V
EX2.9
10 − 4.4
vO = 4.4 V , I = = 0.5895 mA
9.5
Set I = ID1, then vI = 4.4 − 0.6 − ( 0.5895 )( 0.5 ) = 3.505 V
Summary: For 0 ≤ vI ≤ 3.5 V , vO = 4.4 V
For vI > 3.5 V , D2 turns on and when vI ≥ 9.4 V , vO = 10 V
␯O(V)
10
4.4
0
3.505 9.4 ␯I (V)
EX2.10
VO = −0.6 V , I D1 = 0
−0.6 − ( −10 )
ID2 = I = ⇒ I D 2 = I = 4.27 mA
2.2
EX2.11
At the VA node:
15 − VA V
= ID2 + A (1)
5 15
At the VB node:
15 − (VB + 0.7 ) V
+ I D 2 = B (2)
5 10
We see that
VB = VA − 0.7, so Equation (2) becomes
15 − VA V − 0.7
+ ID2 = A (2’)
5 10
Solving for ID2 from Equation (1) and substituting into Equation (2’), we find
⎛ 15 − VA ⎞ VA VA − 0.7
2⎜ ⎟− =
⎝ 5 ⎠ 15 10
Then VA = 10.71 V and VB = 10.01 V
15 − 10.71
Solving for the diode currents, we obtain I D1 = ⇒ I D1 = 0.858 mA
5

4. 15 − 10.71 10.71
Also I D 2 = − ⇒ I D 2 = 0.144 mA
5 15
EX2.12
Assuming all diodes are conducting, we have VB = −0.7 V and VA = 0
Summing currents, we have
5 − VA
= I D1 + I D 2 (1)
5
V − ( −5 )
I D 2 + I D3 = B (2)
5
V − ( −10 ) 10 − 0.7
I D1 = B = (3)
10 10
From ( 3) , we find
I D1 = 0.93 mA
From (1) , we obtain
I D 2 = 0.07 mA
From ( 2 ) , we have
I D 3 = 0.79 mA
EX2.13
(a) I ph = η eΦ
⎡ 6.4 × 10 −2 ⎤
so I = ( 0.8 ) (1.6 × 10−19 ) ⎢ ⎥ ( 0.5 )
⎢ ( 2 ) (1.6 × 10−19 ) ⎥
⎣ ⎦
or I ph = 12.8 mA
(b) We have vO = (12.8)(1) = 12.8 V .
The diode must be reverse biased so that VPS > 12.8 V
EX2.14
The equivalent circuit is
ϩ5 V
ϩ
Vr ϭ 1.7 V
Ϫ
rf ϭ 15 ⍀
I
R
0.2 V
5 − 1.7 − 0.2
So I = = 15 mA
rf + R
15 − 1.7 − 0.2 3.1
Or rf + R = = = 0.207 kΩ
15 15
Then R = 207 − 15 ⇒ R = 192 Ω
2.15
40 − 12
(a) IZ = = 0.233 A
120
P = ( 0.233)(12 ) = 2.8 W

5. (b) I R = 0.233 A, I L = ( 0.9 )( 0.233) = 0.21 A
12
So 0.21 = ⇒ RL = 57.1 Ω
RL
(c) P = ( 0.1)( 0.233)(12 ) ⇒ P = 0.28 W
Test Your Understanding Exercises
TYU2.1
vI = 120sin ( 2π 60t ) , Vγ = 0.7 V , and R = 2.5 kΩ
Full-wave rectifier: Turns ratio 1:2 so that
vS = v I
VM = 120 − 0.7 = 119.3 V
Vr = 119.3 − 100 = 19.3 V
VM 119.3
So C = = or C = 20.6 μ F
2 f RVr 2 ( 60 ) ( 2.5 x103 ) (19.3)
TYU2.2
vI = 50sin ( 2π 60t ) , Vγ = 0.7 V , and R = 10 kΩ. Full-wave rectifier
VM ( 50 − 1.4 )
C= =
2 f RVr 2 ( 60 ) (10 × 103 ) ( 2 )
or C = 20.3 μ F
TYU2.3
Using Equation (2.10)
2Vr 2 ( 4)
(a) ω Δt = = = 0.327
VM 75
⎛ 0.327 ⎞
Percent time = ⎜ ⎟ × 100% = 5.2%
⎝ 2π ⎠
2Vr 2 (19.3)
(b) ω Δt = = = 0.569
VM 119.3
⎛ 0.569 ⎞
Percent time = ⎜ ⎟ × 100% = 18.1%
⎝ π ⎠
2Vr 2 ( 2)
(c) ω Δt = = = 0.287
VM 48.6
⎛ 0.287 ⎞
Percent time = ⎜ ⎟ × 100% = 9.14%
⎝ π ⎠
TYU2.4
V − VZ
I Z = PS − IL
Ri
11 − 9
For VPS (min) and IL (max), then I Z ( min ) = − 0.1 = 0 (Minimum Zener current is zero.)
20
13.6 − 9
For VPS (max) and IL (min), then I Z ( max ) = − 0 ⇒ I Z ( max ) = 230 mA
20
The characteristic of the minimum Zener current being one-tenth of the maximum value is violated.
The proper circuit operation is questionable.
TYU2.5

6. VPS ( min ) − VZ
I Z ( min ) = − I L ( max )
Ri
10 − 9
so 30 = − I L ( max ) which yields I L ( max ) = 35.4 mA
0.0153
TYU2.6
␯O(V)
4.35
2.7
Ϫ4.7
2.7 6 ␯I (V)
Ϫ4.7
TYU2.7
As vS goes negative, D turns on and vO = +5 V . As vS goes positive, D turns off. Output is a square
wave oscillating between +5 and +35 volts.
TYU2.8
␯O(V)
4.4
0 0.6 5 ␯I (V)
(a)
␯O(V)
4.4
2.4
0 3 5 ␯I (V)
(b)

7. TYU2.9
(a) VO = 0.6 V for all V1.
VO (V)
3.6
0.6
0 3 VI (V)
(b)
PSpice Exercises