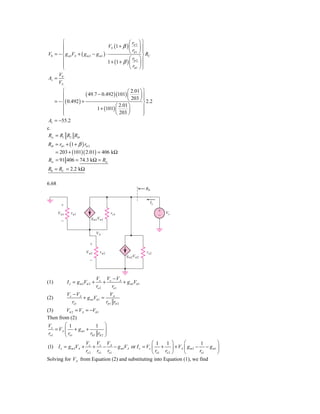
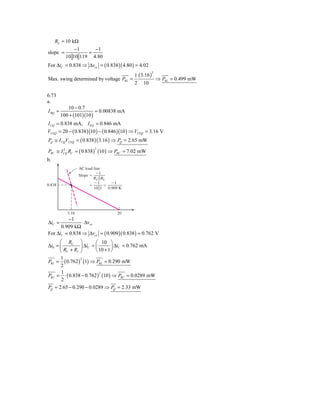
This document contains solutions to problems involving BJT amplifier circuit analysis. Problem 6.1 calculates key transistor parameters like transconductance (gm) and output resistance (ro) for two common-emitter amplifiers. Problem 6.2 repeats this calculation for different bias currents. Subsequent problems analyze additional amplifier circuits, determining voltage gains and component values needed to meet specified conditions. Calculations involve setting up and solving equations relating bias currents, voltages, transistor parameters and circuit resistances.

1. Chapter 6
Problem Solutions
6.1
a.
I CQ 2
gm = = ⇒ g m = 76.9 mA/V
VT 0.026
β VT (180 )( 0.026 )
rπ = = ⇒ rπ = 2.34 kΩ
I CQ 2
VA 150
r0 = = ⇒ r0 = 75 kΩ
I CQ 2
b.
0.5
gm = ⇒ g m = 19.2 mA/V
0.026
(180 )( 0.026 )
rπ = ⇒ rπ = 9.36 kΩ
0.5
150
r0 = ⇒ r0 = 300 kΩ
0.5
6.2
(a)
I CQ 0.8
gm = = = 30.8 mA/V
VT 0.026
β VT (120 )( 0.026 )
rπ = = = 3.9 K
I CQ 0.8
VA 120
ro = = = 150 K
I CQ 0.8
(b)
0.08
gm = = 3.08 mA/V
0.026
(120 )( 0.026 )
rπ = = 39 K
0.08
120
ro = = 1500 K
0.08
6.3
I CQ I CQ
gm = ⇒ 200 = ⇒ I CQ = 5.2 mA
VT 0.026
β VT (125)( 0.026 )
rπ = = ⇒ rπ = 0.625 kΩ
I CQ 5.2
VA 200
r0 = = ⇒ r0 = 38.5 kΩ
I CQ 5.2
6.4

2. I CQ I CQ
gm = ⇒ 80 = ⇒ I CQ = 2.08 mA
VT 0.026
β VT β ( 0.026 )
rπ = ⇒ 1.20 = ⇒ β = 96
I CQ 2.08
6.5
(a)
2 − 0.7
I BQ = = 0.0052 mA
250
I C = (120 )( 0.0052 ) = 0.624 mA
0.624
gm = ⇒ g m = 24 mA / V
0.026
(120 )( 0.026 )
rπ = ⇒ rπ = 5 k Ω
0.624
ro = ∞
⎛ r ⎞ ⎛ 5 ⎞
(b) Av = − g m RC ⎜ π ⎟ = − ( 24 )( 4 ) ⎜ ⎟ ⇒ Av = −1.88
⎝ rπ + RB ⎠ ⎝ 5 + 250 ⎠
v v
(c) vS = O = O ⇒ vS = −0.426sin100t V
Av −1.88
6.6
I CQ
gm = , 1.08 ≤ I CQ ≤ 1.32 mA
VT
1.08 1.32
≤ gm ≤ ⇒ 41.5 ≤ g m ≤ 50.8 mA/V
0.026 0.026
β VT (120 )( 0.026 )
rπ = ; rπ ( max ) = = 2.89 kΩ
I CQ 1.08
(80 )( 0.026 )
rπ ( min ) = = 1.58 kΩ
1.32
1.58 ≤ rπ ≤ 2.89 kΩ
6.7
a.
β VT (120 )( 0.026 )
rπ = 5.4 = = ⇒ I CQ = 0.578 mA
I CQ I CQ
1 1
VCEQ = VCC = ( 5 ) = 2.5 V
2 2
VCEQ = VCC − I CQ RC ⇒ 2.5 = 5.0 − ( 0.578 ) RC ⇒ RC = 4.33 kΩ
I CQ 0.578
I BQ = = = 0.00482 mA
β 120
VBB = I BQ RB + VBE ( on )
= ( 0.00482 )( 25 ) + 0.70 ⇒ VBB = 0.820 V
b.

3. β VT (120 )( 0.026 )
rπ = = = 5.40 kΩ
I CQ 0.578
I CQ 0.578
gm = = = 22.2 mA/V
VT 0.026
VA 100
r0 = = = 173 kΩ
I CQ 0.578
⎛ r ⎞
V0 = − g m ( r0 RC ) Vπ , Vπ = ⎜ π ⎟ VS
⎝ rπ + RB ⎠
⎛ r ⎞ β ( r0 RC )
Av = − g m ⎜ π ⎟ ( r0 RC ) = −
⎝ rπ + RB ⎠ rπ + RB
(120 ) ⎡173
⎣ 4.33⎤
⎦ (120 )( 4.22 )
Av = − =− ⇒ Av = −16.7
5.40 + 25 30.4
6.8
a.
1
VECQ = VCC = 5 V
2
VECQ = 10 − I CQ RC ⇒ 5 = 10 − ( 0.5 ) RC ⇒ RC = 10 kΩ
I CQ 0.5
I BQ = = = 0.005
β 100
VEB ( on ) + I BQ RB = VBB = ( 0.70 ) + ( 0.005 )( 50 ) ⇒ VBB = 0.95 V
b.
I CQ 0.5
gm = = ⇒ g m = 19.2 mA/V
VT 0.026
β VT (100 )( 0.026 )
rπ = = ⇒ rπ = 5.2 kΩ
I CQ 0.5
VA ∞
r0 = = ⇒ r0 = ∞
I CQ 0.5
c. Av = −
β RC
=−
(100 )(10 ) ⇒ A = −18.1
v
rπ + RB 5.2 + 50
6.9
10 − 4
I CQ = = 1.5 mA
4
1.5
I BQ = = 0.015 mA
100
(100 )( 0.026 )
rπ = = 1.73 K
1.5
v 5sin ω t ( mV )
ib = be = = 2.89sin ω t ( μ A )
rπ 1.73 kΩ
So

4. iB ( t ) = I BQ + iEb = 15 + 2.89sin ω t ( μ A )
iC1 ( t ) = β iB ⇒ iC1 ( t ) = 1.5 + 0.289sin ω t ( mA )
vC ( t ) = 10 − iC1 ( t ) RC = 10 − [1.5 + 0.289sin ω t ] (γ )
vC1 ( t ) = 4 − 1.156sin ω t ( v )
vC ( t ) −1.156
Av = = ⇒ Av = −231
vbe ( t ) 0.005
6.10
vo = 1.2sin ω t ( V )
−1.2sin ω t
iC ( t ) RC + vo = 0 ⇒ iC ( t ) =
2
iC ( t ) = −0.60sin ω t ( mA )
iC ( t )
ib ( t ) = = −6sin ω t ( μ A )
β
vbe ( t ) = ib ( t ) ⋅ rπ g m rπ = β
100
rπ = =2K
50
vbe ( t ) = −12sin ω t ( mV )
6.11
a.
I CQ ≈ I EQ
VCEQ = 5 = 10 − I CQ ( RC + RE )
= 10 − I CQ (1.2 + 0.2)
I CQ = 3.57 mA
3.57
I BQ = = 0.0238 mA
150
R1 R2 = RTH = ( 0.1)(1 + β ) RE
= ( 0.1)(151)( 0.2 ) = 3.02 kΩ
1
VTH = ⋅ RTH ⋅ (10) − 5
R1
VTH = I BQ RTH + VBE ( on ) + (1 + β ) I BQ RE − 5
1
(3.02)(10) − 5 = ( 0.0238)(3.02) + 0.7 + (151)( 0.0238)( 0.2) − 5
R1
1
( 30.2 ) = 1.50 ⇒ R1 = 20.1 k Ω
R1
20.1R2
= 3.02 ⇒ R2 = 3.55 kΩ
20.1 + R2
b.
(150 )( 0.026 )
rp = = 1.09 kΩ
3.57
3.57
gm = = 137 mA/V
0.026

5. V0
ϩ
V␲ r␲ gmV␲
Ϫ
ϩ
VS R1͉͉R2 RC
Ϫ
RE
2 β RC (150 )(1.2 )
Av = =2 ⇒ Av = 2 5.75
rp + (1 + β ) RE 1.09 + (151)( 0.2 )
6.12
a.
⎛ R2 ⎞ ⎛ 50 ⎞
VTH = ⎜ ⎟ VCC = ⎜ ⎟ (12 ) = 10 V
⎝ R1 + R2 ⎠ ⎝ 50 + 10 ⎠
RTH = R1 R2 = 50 10 = 8.33 kΩ
12 − 0.7 − 10
I BQ = = 0.0119 mA
8.33 + (101)(1)
I CQ = 1.19 mA, I EQ = 1.20 mA
VECQ = 12 − (1.20 )(1) − (1.19 )( 2 )
VECQ = 8.42 V
iC
4
1.19
8.42 12 ␯EC
b.
V0
Ϫ
V␲ r␲ gmV␲
ϩ
ϩ
VS R1͉͉R2 RC
Ϫ
RE

6. (100 )( 0.026 )
rp = = 2.18 kΩ
1.19
V0 = g mVp RC
⎛V ⎞
VS = 2 Vp − ⎜ p + g mVp ⎟ RE
⎝ rp ⎠
⎡ rπ + (1 + β ) RE ⎤
= −Vp ⎢ ⎥
⎣ rp ⎦
2 β RC 2 (100 )( 2 )
Av = = ⇒ Av = 2 1.94
rp + (1 + β ) RE 2.18 + (101)(1)
c. Approximation: Assume rp does not vary significantly.
RC = 2 kΩ ± 5% = 2.1 kΩ or 1.9 kΩ
RE = 1 kΩ ± 5% = 1.05 kΩ or 0.95 kΩ
For RC ( max ) = 2.1 kΩ and RE ( min )
− (100 )( 2.1)
Av = = −2.14
2.18 + (101)( 0.95 )
For RC ( min ) = 1.9 kΩ and RE ( max ) = 1.05 kΩ
− (100 )(1.9 )
Av = = −1.76
2.18 + (101)(1.05 )
So 1.76 ≤ Av ≤ 2.14
6.13
(a)
VCC = ⎜ 1+ β ⎟ I CQ RE + VECQ + I CQ RC
⎛ ⎞
⎜ ⎟
β
⎝ ⎠
⎛ 101 ⎞
12 = ⎜ ⎟ I CQ (1) + 6 + I CQ ( 2 )
⎝ 100 ⎠
so that I CQ = 1.99 mA
1.99
I BQ = = 0.0199 mA
100
RTH = ( 0.1)(1 + β ) RE = ( 0.1)(101)(1) = 10.1 k Ω
⎛ R2 ⎞ 1 1
VTH = ⎜ ⎟ V = ⋅ R ⋅ V = (10.1)(12 )
⎝ R1 + R2 ⎠ CC R1 TH CC R1
VCC = (1 + β ) I BQ RE + VEB ( on ) + I BQ RTH + VTH
121.2
12 = (101)( 0.0199)(1) + 0.7 + ( 0.0199)(10.1) +
R1
which yields R1 = 13.3 k Ω and R2 = 41.6 k Ω
2 β RC 2 (100 )( 2 )
(b) Av = = ⇒ Av = 2 1.95
rp + (1 + β ) RE 1.31 + (101)(1)
6.14

7. I CQ = 0.25 mA, I EQ = 0.2525 mA
I BQ = 0.0025 mA
I BQ RB + VBE ( on ) + I EQ ( RS + RE ) − 5 = 0
( 0.0025)( 50 ) + 0.7 + ( 0.2525)( 0.1 + RE ) = 5
RE = 16.4 kΩ
VE = − ( 0.0025 )( 50 ) − 0.7 = −0.825 V
VC = VCEQ + VE = 3 − 0.825 = 2.175 V
5 − 2.175
RC = ⇒ RC = 11.3 kΩ
0.25
− β RC
Av =
rπ + (1 + β ) RS
(100 )( 0.026 )
rπ = = 10.4 kΩ
0.25
− (100 )(11.3)
Av = ⇒ Av = −55.1
10.4 + (101)( 0.1)
Ri = RB ⎡ rπ + (1 + β ) RS ⎤
⎣ ⎦
= 50 ⎡10.4 + (101)( 0.1) ⎤
⎣ ⎦
Ri = 50 20.5 ⇒ Ri = 14.5 kΩ
6.15
(a)
VCC > I CQ ( RC + RE ) + VCEQ
9 = I CQ ( 2.2 + 2 ) + 3.75 So that
I CQ = 1.25 mA
Assume circuit is to be designed to be bias stable.
RTH = R1 R2 = ( 0.1)(1 + β ) RE = ( 0.1)(121)( 2 ) = 24.2 Ω
1.25
I BQ = = 0.01042 mA
120
1
VTH = ⋅ RTH ⋅ VCC = I BQ RTH + VBE ( on ) + I BQ (121)( RE )
R1
1
( 24.2 )( 9 ) = ( 0.01042 )( 24.2 ) + 0.7 + ( 0.01042 )(121)( 2 )
R1
= 0.2522 + 0.7 + 2.5216
= 3.474
62.7 R2
R1 = 62.7 K = 24.2
62.7 + R2
R2 = 39.4 K
(b)

8. 1.25
gm = = 48.08 mA / V
0.026
(120 )( 0.026 )
rp = = 2.50 k Ω
1.25
100
ro = = 80 k Ω
1.25
Vo
ϩ
IS V␲ r␲ ro RC RL
R1͉͉R2Ϫ gmV␲
Vo = 2 g mVp ( ro RC RL )
Vp = I S ( R1 R2 rp )
Then
Vo
Rm = = 2 g m ( R1 R2 rp )( ro RC RL )
Is
Rm = 2 48.08 ( 24.2 2.5 )( 80 2.2 1) = 2 48.08 ( 2.266 )( 0.6816 )
or
Vo
Rm = = −74.3 k Ω = −74.3 V / mA
Is
6.16
a.
0.80
I EQ = 0.80 mA, I BQ = = 0.0121 mA
66
I CQ = 0.788 mA
0.3
VB = I BQ RB ⇒ RB = ⇒ RB = 24.8 kΩ
0.0121
V − ( −5 ) 5 − 3
RC = C = ⇒ RC = 2.54 kΩ
I CQ 0.788
b.
0.788
gm = = 30.3 mA / V
0.026
( 65)( 0.026)
rπ = = 2.14 kΩ
0.788
75
r0 = = 95.2 kΩ
0.788
⎛ RC r0 ⎞
i0 = ⎜ g V , V = − vS
⎜R r +R ⎟ m π π⎟
⎝ C 0 L ⎠
i0 ⎛ RC r0 ⎞
Gf = = − gm ⎜ ⎟
vS ⎜R r +R ⎟
⎝ C 0 L ⎠
⎛ 2.54 95.2 ⎞
= − ( 30.3) ⎜
⎜ 2.54 95.2 + 4 ⎟
⎟
⎝ ⎠
G f = −11.6 mA/V

9. 6.17
(a)
I CQ = 0.8 mA ⇒ I BQ = 0.00667 mA
I BQ RS + 0.7 + (121) I BQ RE − 15 = 0
( 0.01667 )( 2.5) + 0.7 + (121)( 0.00667 ) RE = 15
RE = 17.7 K
VE = − ( 0.00667 )( 2.5 ) − 0.7 = −0.717 V
VC = −0.717 + 7 = 6.283 V
15 − 6.283
RC = = 10.9 K
0.8
0.8 (120 )( 0.026 )
gm = = 30.77 mA/V rπ = = 3.9 K
0.026 0.8
⎛ r ⎞
vo = − g m ( RC RL ) ⋅ vπ vπ = ⎜ π ⎟ vS
⎝ rπ + RS ⎠
− β ( RC RL ) − (120 ) (10.9 5 )
Av = =
rπ + RS 3.9 + 2.5
Av = −64.3
(b) For RS = 0
0.7 + (121)( 0.00667 ) RE = 15
RE = 17.7 K
VE = −0.7 ⇒ VC = −0.7 + 7 = 6.3
15 − 6.3
RC = ⇒ RC = 10.9 K
0.8
− β ( RC RL )
Av = = −30.77 (10.9 5 )
rπ
Av = −105
6.18
(a)
15 = ( 81) I BQ (10 ) + 0.7 + I BQ ( 2.5 )
15 − 0.7
I BQ = = 0.0176 mA
2.5 + ( 81)(10 )
I CQ = 1.408 mA
1.408 (80 )( 0.026 )
gm = = 54.15 mA/V rπ =
0.026 1.408
rπ = 1.48 K
RS
V0
IS
ϩ
VS ϩ V␲ r␲ RC Io RL
Ϫ gmV␲
Ϫ

10. − β ( RC RL ) − ( 80 ) ( 5 5 )
Vo = − g mVσ ( RC RL ) ⇒ Av = = ⇒ Av = −50.3
rπ + RS 1.48 + 2.5
⎛ RC ⎞
− g mVπ ⎜ ⎟
i
AI = o = ⎝ RC + RL ⎠ = − β ⎛ RC ⎞
V ⎜ ⎟
iS π ⎝ RC + RL ⎠
r
π
AI = −40
vo ( t ) = ( −50.3)( 4sin ω t )
vo ( t ) = −0.201sin ω t ( V )
4 sin ω t ( mV )
is = = 1.005sin ω t ( μA )
2.5 + 1.48
io = −40.2 sin ω t ( μA )
(b)
15 − 0.7
I EQ = = 1.43 mA
10
⎛ 80 ⎞
I CQ = ⎜ ⎟ (1.43) = 1.412 mA
⎝ 81 ⎠
1.412 (80 )( 0.026 )
gm = = 54.3 mA/V rπ = = 1.47 K
0.026 1.412
Av = − g m ( RC RL ) = − ( 54.3) ( 5 5 ) ⇒ Av = −136
⎛ RC ⎞ ⎛ 5 ⎞
AI = − β ⎜ ⎟ = −80 ⎜ ⎟ ⇒ AI = −40
⎝ RC + RL ⎠ ⎝5+5⎠
vo ( t ) = ( −136 )( 4sin ω t ) ⇒ vo ( t ) = −544sin ω t ⇒ vo ( t ) = −0.544sin ω t ( V )
4sin ω t ( mV )
is ( t ) = = 2.72sin ω t ( μA )
1.47 k
io ( t ) = ( −40 )( 2.72sin ω t )
io ( t ) = −109sin ω t ( μA )
6.19
RTH = R1 R2 = 27 15 = 9.64 K
⎛ R2 ⎞ ⎛ 15 ⎞
VTH = ⎜ ⎟ VCC = ⎜ ⎟ ( 9 ) = 3.214 V
⎝ R1 + R2 ⎠ ⎝ 15 + 27 ⎠
V − VBE ( on ) 3.214 − 0.7 2.514
I BQ = TH = =
RTH + (1 + β ) RE 9.64 + (101)(1.2 ) 130.84
I BQ = 0.0192 mA I CQ = 1.9214 mA
1.92 (100 )( 0.026 )
gm = = 73.9 mA/V rπ = = 1.35 K
0.026 1.92

11. RS
V0
IS
ϩ
VS ϩ RTH V␲ r␲ r0 RC I0 RL
Ϫ gmV␲
Ϫ
100
ro = = 52.1 K
1.92
⎛ r R ⎞
(
Vo = − g mVπ r0 RC RL ) Vπ = ⎜ π TH
⎜r R +R ⎟ VS
⎟
⎝ π TH S ⎠
rπ RTH = 1.35 9.64 = 1.184 K
⎛ 1.184 ⎞
Vπ = ⎜ ⎟ VS
⎝ 1.184 + 10 ⎠
= 0.1059VS
(
Av = − ( 73.9 ) ( 0.1059 ) 52.1 2.2 2 )
= − ( 73.9 ) ( 0.1059 ) ( 52.1 1.0476 )
= − ( 73.9 ) ( 0.1059 ) (1.027 )
Av = −8.04
⎛ ro RC ⎞
− g mVπ ⎜
⎜r R +R ⎟
⎟
I ⎝ o C L ⎠
AI = o =
IS Vπ
RTH rπ
⎛ ro RC ⎞
AI = − g m ( RTH rπ ) ⎜
⎜r R +R ⎟ ⎟
⎝ o C L ⎠
ro RC = 52.1 2.2 = 2.11 K
RTH rπ = 9.64 1.35 = 1.184 K
⎛ 2.11 ⎞
AI = − ( 73.9 ) (1.184 ) ⎜ ⎟
⎝ 2.11 + 2 ⎠
AI = −44.9
Ri = RTH rπ = 9.64 1.35
Ri = 1.184 K
6.20
a.
0.35
I E = 0.35 mA, I B = = 0.00347 mA
101
VB = 2 I B RB = 2 ( 0.00347 )(10 ) ⇒ VB = 2 0.0347 V
VE = VB − VBE ( on ) ⇒ VE = 2 0.735 V
b.

12. VC = VCEQ + VE = 3.5 − 0.735 = 2.77 V
⎛ b ⎞ ⎛ 100 ⎞
IC = ⎜ ⎟ IE = ⎜ ⎟ ( 0.35 ) = 0.347 mA
⎝ 1+ b ⎠ ⎝ 101 ⎠
V 1 − VC 5 − 2.77
RC = = ⇒ RC = 6.43 kΩ
IC 0.347
(c)
⎛ RB rp ⎞
⎜ R r + R ⎟( C o )
Av = 2 g m ⎜ R r
⎟
⎝ B π S ⎠
0.347 100
gm = = 13.3 mA/V , ro = = 288 k Ω
0.026 0.347
(100 )( 0.026 )
rp = = 7.49 k Ω
0.347
RB rp = 10 7.49 = 4.28 k Ω
⎛ 4.28 ⎞
Av = 2 (13.3) ⎜ ⎟ ( 6.43 288 ) ⇒ Av = 2 81.7
⎝ 4.28 + 0.1 ⎠
d.
⎛ RB rp ⎞
⎜ R r + R ⎟( C 0 )
Av = 2 g m ⎜ R r
⎟
⎝ B p S ⎠
RB rp = 10 7.49 = 4.28 kΩ
⎛ 4.28 ⎞
Av = 2 (13.3) ⎜ ⎟ ( 6.43 288 ) ⇒ Av = 2 74.9
⎝ 4.28 + 0.5 ⎠
6.21
a.
RTH = R1 R2 = 6 1.5 = 1.2 kΩ
⎛ R2 ⎞ + ⎛ 1.5 ⎞
VTH = ⎜ ⎟V = ⎜ ⎟ ( 5 ) = 1.0 V
⎝ R1 + R2 ⎠ ⎝ 1.5 + 6 ⎠
V − VBE ( on ) 1.0 − 0.7
I BQ = TH = = 0.0155 mA
RTH + (1 + β ) RE 1.2 + (181)( 0.1)
I CQ = 2.80 mA, I EQ = 2.81
VCEQ = V + − I CQ RC − I EQ RE
= 5 − ( 2.8 )(1) − ( 2.81)( 0.1) ⇒ VCEQ = 1.92 V
b.
(180 )( 0.026 )
rp = ⇒ rp = 1.67 kΩ
2.80
2.80
gm = ⇒ g m = 108 mA/V, r0 =`
0.026
(c)
⎛ R1 R2 rp ⎞
Av = 2 g m ⎜ ⎟ ( RC RL )
⎝ R1 R2 rp + RS ⎠
R1 R2 rp = 6 1.5 1.67 = 0.698 k V
⎛ 0.698 ⎞
Av = 2 (108 ) ⎜ ⎟ (1 1.2 ) ⇒ Av = 2 45.8
⎝ 0.698 + 0.2 ⎠

13. 6.22
a.
9 = I EQ RE + VEB ( on ) + I BQ RS
0.75
I EQ = 0.75 mA, I BQ = = 0.00926 mA
81
I CQ = 0.741 mA
9 = ( 0.75 ) RE + 0.7 + ( 0.00926 )( 2 ) ⇒ RE = 11.0 kΩ
b.
VE = 9 − ( 0.75 )(11) = 0.75 V
VC = VE − VECQ = 0.75 − 7 = −6.25 V
VC − ( −9 ) 9 − 6.25
RC = = ⇒ RC = 3.71 kΩ
I CQ 0.741
c.
⎛ rp ⎞
Av = 2 g m ⎜ ⎟ ( RC || RL || r0 )
⎝ rp + RS ⎠
(80 )( 0.026 )
rp = = 2.81 kΩ
0.741
80
r0 = = 108 kV
0.741
2 80
Av = ( 3.71||10 ||108 )
2.81 + 2
Av = 2 43.9
d.
Ri = RS + rp = 2 + 2.81 ⇒ Ri = 4.81 kΩ
6.23
4 − 0.7
I BQ = = 0.00647
5 + (101)( 5 )
I CQ = 0.647 mA
a. 80 ≤ h fe ≤ 120, 10 ≤ h0e ≤ 20 mS
2.45 kΩ ≤ hie ≤ 3.7 kΩ
low gain high gain
RS
V0
IS
ϩ
VS ϩ V␲ r␲ RC Io RL
Ϫ gmV␲
Ϫ

14. ⎛ 1 ⎞
V0 = 2 h fe I b ⎜ RC RL ⎟
⎝ hoe ⎠
RB
V
?S
R + RS
Ib = B
RTH + hie
RTH = RB RS = 5 1 = 0.833 kΩ
High-gain
⎛ 5 ⎞
⎜ ⎟ VS
5 +1⎠
Ib = ⎝ = 0.1838VS
0.833 + 3.7
Low-gain
⎛ 5 ⎞
⎜ ⎟ VS
Ib = ⎝ 5 +1⎠ = 0.2538VS
0.833 + 2.45
1 1
For hoe = 10 ⇒ || Rc || RL = || 4 || 4
hoe 0.010
= 100 || 2 = 1.96 kΩ
1
For hoe = 20 ⇒ || 4 || 4 = 50 || 2 = 1.92 kΩ
0.020
Av max
= (120 )( 0.1838 )(1.96 ) = 43.2
Av min
= ( 80 )( 0.2538 )(1.92 ) = 39.0
39.0 ≤ Av ≤ 43.2
b.
Ri = RB hie = 5 3.7 = 2.13 kV or Ri = 5 2.45 = 1.64 kΩ
1.64 ≤ Ri ≤ 2.13 kΩ
1 1
R0 = RC = 4 = 100 || 4 = 3.85 kΩ
hoe 0.010
1
or R0 = || 4 = 50 || 4 = 3.70 kΩ
0.020
3.70 ≤ R0 ≤ 3.85 kΩ
6.24
VCC ϭ 10 V
RC
R1
␯o
RS ϭ 1 k⍀
CC
␯s ϩ R2
Ϫ
RE CE

15. Assume an npn transistor with b = 100 and VA = ∞. Let VCC = 10 V .
0.5
Av = = 50
0.01
Bias at I CQ = 1 mA and let RE = 1 k Ω
For a bias stable circuit
RTH = ( 0.1)(1 + b ) RE = ( 0.1)(101)(1) = 10.1 k Ω
1 1 101
VTH = ⋅ RTH ⋅ VCC = (10.1)(10 ) =
R1 R1 R1
1
I BQ = = 0.01 mA
100
VTH = I BQ RTH + VBE ( on ) + (1 + b ) I BQ RE
101
= ( 0.01)(10.1) + 0.7 + (101)( 0.01)(1)
R1
which yields R1 = 55.8 k Ω and R2 = 12.3 k Ω
Now
(100 )( 0.026 )
rp = = 2.6 k Ω
1
1
gm = = 38.46 mA/V
0.026
Vo = − g mVp RC
⎛ R1} R2 } rp ⎞ ⎛ 10.1} 2.6 ⎞
where Vp = ⎜ ⎟ ⋅ Vs = ⎜ ⎟ .Vs
⎝ R1} R2 } rp + RS ⎠ ⎝ 10.1} 2.6 + 1 ⎠
or Vp = 0.674 Vs
V
Then Av = o = − ( 0.674 ) g m RC = − ( 0.674 )( 38.46 ) RC = −50
Vs
which yields RC = 1.93 k Ω
With this RC, the dc bias is OK.
Finish Design, Set RC = 2 K RE = 1 K
R1 = 56 K
R2 = 12 K
RTH = R1 R2 = 9.88 K
⎛ R2 ⎞ ⎛ 12 ⎞
VTH = ⎜ ⎟ VCC = ⎜ ⎟ (10 ) = 1.765 V
⎝ R1 + R2 ⎠ ⎝ 12 + 56 ⎠
1.765 − 0.7
I BQ = = 9.60 μ A
9.88 + (101)(1)
I CQ = 0.9605 mA
(100 )( 0.026 ) 0.9605
rπ = = 2.707 K gm = = 36.94
0.9605 0.026
RTH rπ = 2.125 K
⎛ RTH rπ ⎞ ⎛ 2.125 ⎞
Vπ = ⎜ ⎟ Vi = ⎜ ⎟ Vi = ( 0.680 ) Vi
⎝ RTH rπ + RS ⎠ ⎝ 2.125 + 1 ⎠
Av = − ( 0.680 ) g m RC = − ( 0.680 )( 36.94 )( 2 ) = −50.2

16. Design specification met.
6.25
a.
6 − 0.7
I BQ = = 0.0169 mA
10 + (101)( 3)
I CQ = 1.69 mA, I EQ = 1.71 mA
VCEQ = (16 + 6 ) − (1.69 )( 6.8 ) − (1.71)( 3)
VCEQ = 5.38 V
b.
1.69
gm = ⇒ g m = 65 mA/V
0.026
(100 )( 0.026 )
rp = ⇒ rp = 1.54 kV , r0 = ∞
1.69
(c)
− β ( RC RL ) RB Rib
Av = ⋅
rπ + (1 + β ) RE RB Rib + RS
Rib = rπ + (1 + β ) RE = 1.54 + (101)(3) = 304.5 k Ω
RB Rib = 10 304.5 = 9.68 k Ω
Then
− (100 )( 6.8 6.8 ) ⎛ 9.68 ⎞
Av = ⋅⎜ ⎟ ⇒ Av = −1.06
1.54 + (101)( 3) ⎝ 9.68 + 0.5 ⎠
⎛ RC ⎞
i0 = ⎜ ⎟ ( − β ib )
⎝ RC + RL ⎠
⎛ RB ⎞
ib = ⎜ ⎟ iS
⎝ RB + rπ + (1 + β ) RE ⎠
⎛ RC ⎞⎛ RB ⎞
Ai = − ( β ) ⎜ ⎟⎜⎜ R + r + (1 + β ) R ⎟ ⎟
⎝ RC + RL ⎠⎝ B π E ⎠
⎛ 6.8 ⎞ ⎛ 10 ⎞
= − (100 ) ⎜ ⎟⎜⎜ 10 + 1.54 + (101)( 3) ⎟ ⇒ Ai = −1.59
⎟
⎝ 6.8 + 6.8 ⎠ ⎝ ⎠
(d) Ris = RS + RB Rib = 0.5 + 10 304.5 = 10.2 k Ω
(e)
2 b ( RC RL )
Av =
rp + (1 + b ) RE
2 (100 ) ( 6.8} 6.8 )
Av = ⇒ Av = 2 1.12
1.54 + (101)( 3)
Ai = same as ( c ) ⇒ Ai = 2 1.59
6.26

17. ie
ϩ ϩ
vCE
ϩ vCE ris gmv␲ ␲o
vbe Ϫ
Ϫ
Ϫ
ϩ
vCE gmv␲
Ϫ
vCe 1
r= =
g m vCe g m
⎛ 1 ⎞
So re = rp ⎜ ⎟ r0
⎝ gm ⎠
6.27
Let b = 100, VA = ∞
VCC
RC
R1
␯o
RS ϭ 100 ⍀
CC
␯s ϩ R2
Ϫ
RE
Let VCC = 2.5 V
P = ( I R + I C ) VCC ⇒ 0.12 = ( I R + I C )( 2.5 ) ⇒ I R + I C = 48 mA, Let I R = 8mA, I C = 40 mA
VCC 2.5
R1 + R2 > = ⇒ 312.5 k Ω
IR 8
40
I BQ = = 0.4 mA
100

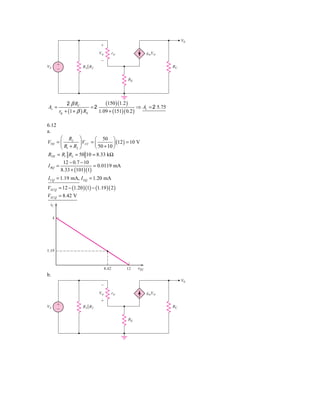
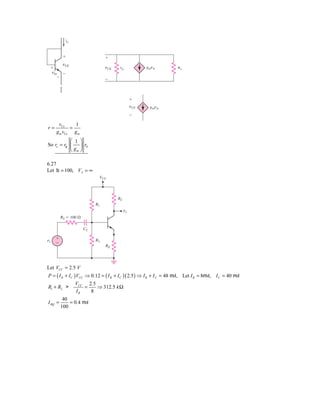
18. Let RE = 2 k Ω. For a bias stable circuit
RTH = ( 0.1)(1 + b ) RE = ( 0.1)(101)( 2 ) = 20.2 k Ω
1
VTH = ⋅ RTH ⋅ VCC = I BQ RTH + VBE ( on ) + (1 + b ) I BQ RE
R1
1
( 20.2 )( 2.5 ) = ( 0.0004 )( 20.2 ) + 0.7 + (101)( 0.0004 )( 2 )
R1
which yields R1 = 64 k V and R2 = 29.5 k Ω
(100 )( 0.026 )
rπ = = 65 k Ω Neglect RS
0.04
Vo 2 b RC
Av = >
Vs rπ + (1 + b ) RE
2 100 RC
−10 = ⇒ RC = 26.7 k Ω
65 + (101)( 2 )
With this RC , dc biasing is OK.
6.28
100
Need a voltage gain of = 20.
5
Assume a sign inversion from a common-emitter is not important. Use the configuration for Figure 6.31.
Let RS = 0. Need an input resistance of
5 × 102 3
Ri = = 25 × 103 = 25 k Ω
0.2 × 102 6
Ri = RTH Rib . Let RTH = 50 k Ω, Rib = 50 k Ω
Rib = rp + (1 + b ) RE > (1 + b ) RE
Rib 50
For b = 100, RE = = = 0.495 k Ω
1 + b 101
Let RE = 0.5 k V , VCC = 10 V , I CQ = 0.2 mA
0.2
Then I BQ = = 0.002 mA
100
VTH = I BQ RTH + VBE ( on ) + (1 + β ) I BQ RE
1 1
⋅ RTH ⋅ VCC = ( 50)(10) = ( 0.002)(50) + 0.7 + (101)( 0.002 )( 0.5)
R1 R1
which yields R1 = 555 k Ω and R2 = 55 k Ω
− β RC (100)( 0.026)
Now Av = , rπ = = 13 k Ω
rπ + (1 + β ) RE 0.2
So
− (100 ) RC
−20 = ⇒ RC = 12.7 k Ω
13 + (101)( 0.5)
[Note: I CQ RC = ( 0.2 )(12.7 ) = 2.54 V. So dc biasing is OK.]
6.29

19. VCC ϭ 10 V
R1 RE
CC
␯o
␯s ϩ R2
Ϫ
RC
2 b RC
b = 80, Av =
rp + (1 + b ) RE
First approximation:
R
( Av ) ≈ C = 10 ⇒ RC = 10 RE
RE
Set RC = 12 RE
VEC ≈ VCC − I C ( RC + RE ) = 10 − I C (13RE )
1
For VEC = VCC = 5
2
5 = 10 − I C (13RE )
For I C = 0.7 mA
I E = 0.709, I B = 0.00875 mA ⇒ RE = 0.55 kΩ − RC = 6.6 kΩ
Bias stable ⇒
R1 R2 = RTH = ( 0.1)(1 + β ) RE
= ( 0.1)(81)( 0.55 ) = 4.46 kΩ
1
10 = ( 0.709 )( 0.55 ) + 0.7 + ( 0.00875 )( 4.46 ) + ( 4.46 )(10 )
R1
1
8.87 = ( 4.46 ) ⇒ R1 = 5.03 kΩ
R1
5.03R2
= 4.46 ⇒ R2 = 39.4 kΩ
5.03 + R2
10 10
= = 0.225 mA
R1 + R2 5.03 + 39.4
0.7 + 0.225 ≅ 0.925 mA from VCC source.
(80 ) ( 0.026 )
Now rπ = = 2.97 kΩ
0.7
(80 )( 6.6 )
Av = = 11.1
2.97 + ( 81)( 0.55 )
6.30

20. ϩ5V
R1 RC
CC2
CC1 ␯o
RL ϭ 10 K
␯s ϩ
Ϫ R2 CE
RE
Ϫ5V
β = 120
Let I CQ = 0.35 mA, I EQ = 0.353 mA
I BQ = 0.00292 mA
Let RE = 2 kΩ. For VCEQ = 4 V ⇒ 10 = 4 + ( 0.35) RC + ( 0.353)( 2)
(120 )( 0.026 )
RC = 15.1 kΩ, rπ = = 8.91 kΩ
0.35
− β ( RC RL ) (120 ) (15.1 10 )
Av = =−
rπ 8.91
Av = −81.0
For bias stable circuit:
R1 R2 = RTH = ( 0.1)(1 + β ) RE
= ( 0.1)(121)( 2 ) = 24.2 kΩ
⎛ R2 ⎞ 1
VTH = ⎜ ⎟ (10) − 5 = ⋅ RTH ⋅ (10 ) − 5
⎝ R1 + R2 ⎠ R1
VTH = I BQ RTH + VBE ( on ) + (1 + β ) I BQ RE − 5
1
( 24.2 )(10 ) − 5 = ( 0.00292 )( 24.2 ) + 0.7 + (121)( 0.00292 )( 2 ) − 5
R1
1
( 242 ) = 1.477, R1 = 164 kΩ
R1
164 R2
= 24.2 ⇒ R2 = 28.4 kΩ
164 + R2
10
= 0.052, 0.35 + 0.052 = 0.402 mA
164 + 28.4
So bias current specification is met.
6.31
From Prob. 6.12,

21. RTH = R1} R2 = 10}50 = 8.33 kΩ
⎛ R2 ⎞ ⎛ 50 ⎞
VTH = ⎜ ⎟ (12 ) = ⎜ ⎟ (12 ) = 10 V
⎝ R1 + R2 ⎠ ⎝ 50 + 10 ⎠
12 − 0.7 − 10
I BQ = = 0.0119 mA
8.33 + (101)(1)
I CQ = 1.19 mA, I EQ = 1.20 mA
VECQ = 12 − (1.19 )( 2 ) − (120 )(1) = 8.42 V
1.19
1 8.42 11 12
For 1 ≤ vEC ≤ 11
DvEC = 11 − 8.42 = 2.58
⇒ Output voltage swing = 5.16 V (peak-to-peak)
6.32
5 − 0.7
I BQ = = 0.00315 mA
50 + (101)( 0.1 + 12.9)
I CQ = 0.315 mA, I EQ = 0.319 mA
VCEQ = ( 5 + 5 ) − ( 0.315 )( 6 ) − ( 0.319 )(13)
VCEQ = 3.96 V
AC load line
Ϫ1
Slope ϭ
6.1 K
0.315
3.96 10
1
ΔiC = − Δv
6.1 eC
For ΔiC = 0.315 − 0.05 = 0.265 ⇒ ΔvEC = 1.62
vEC ( min ) = 3.96 − 1.62 = 2.34
Output signal swing determined by current:

22. Max. output swing = 3.24 V peak-to-peak
6.33
From Problem 4.18, I CQ = 1.408 mA, I EQ = 1.426 mA
(a) VECQ = 30 − (1.408 )( 5 ) − (1.426 )(10 ) = 8.7 V
IC (mA)
AC load line
Ϫ1
Slope ϭ
RC ͉͉RL
Ϫ1
1.408 ϭ
2.5 kΩ
8.7 ␯EC (V)
vEC ( max ) = 8.7 + ΔI C ⋅ ( 2.5 ) = 8.7 + (1.408 )( 2.5 ) = 12.22
Set vEC ( max ) = 12 = 8.7 + ΔI C ( 2.5 ) ⇒ ΔI C = 1.32 mA
So ΔvEC (peak-to-peak) = 2(12 − 8.7) = 6.6 V
(b) ΔiC (peak-to-peak) = 2(1.32) = 2.64 mA
6.34
I EQ = 0.80 mA, I CQ = 0.792 mA
I BQ = 0.00792 mA
VE = 0.7 + ( 0.00792 )(10 ) = 0.779 V
VC = I CQ RC − 5 = ( 0.792 )( 4 ) − 5 = 2 1.83 V
VECQ = 0.779 − ( −1.83) = 2.61 V
Load line: Assume VE remains constant at ≈ 0.78 V
IC (mA)
AC load line
Ϫ1
Slope ϭ
RC ͉͉RL
Ϫ1
1.408 ϭ
2.5 kΩ
8.7 ␯EC (V)
21
DiC = v
? ec
2 kV
Collector current swing = 0.792 − 0.08
= 0.712 mA
Dvec = ( 0.712 )( 2 ) = 1.424 V
Output swing determined by current.
Max. output swing = 2.85 V peak-to-peak
2.85
Swing in i0 current =
4
= 0.712 mA peak-to-peak

23. 6.35
6 − 0.7
I BQ = = 0.0169 mA
10 + (101)( 3)
I CQ = 1.69 mA, I EQ = 1.71 mA
VCEQ = (16 + 6 ) − (1.69 )( 6.8 ) − (1.71)( 3)
VCEQ = 5.38 V
AC load line
Ϫ1
Slope ϭ
3.4 ϩ 3
1.69 Ϫ1
ϭ
6.4 K
5.38 22
1
DiC = 2 Dvce
6.4
4.38
For vce ( min ) = 1 V, Dvce = 5.38 − 1 = 4.38 V ⇒ DiC = = 0.684 mA
6.4
Output swing limited by voltage:
Δvce = Max. swing in output voltage
= 8.76 V peak-to-peak
1
Δi0 = ΔiC ⇒ Δi0 = 0.342 mA
2
or Δi0 = 0.684 mA (peak-to-peak)
6.36
AC load line
Ϫ1
Slope ϭ
1.05 K
2.65
Q-point
ICQ
VCEQ 9
100
ro =
I CQ
Neglect ro as (E) approx. dc load line VCE = 9 − I C ( 3.4 )

24. ΔI C = I CQ − 0.1
ΔVCE = VCEQ − 1
Also ΔVCE = ΔI C ( RC RL ) = ΔI C (1.05 )
Or VCEQ − 1 = ( I CQ − 0.1) (1.05 )
Substituting the expression for the dc load line.
⎡9 − I CQ ( 3.4 ) − 1⎤ = ( I CQ − 0.1) (1.05 )
⎣ ⎦
8.105 = I CQ ( 4.45 ) ⇒ I CQ = 1.821 mA
VCEQ = 2.81 V
1.821
I BQ = = 0.01821
100
RTH = ( 0.1)(101)(1.2 ) = 12.12 K
1 1
VTH = ⋅ RTH ⋅ VCC = (12.12 ) ( 9 ) = ( 0.01821) (12.12 ) + 0.7 + (101)( 0.01821)(1.2 )
R1 R1
= 0.2207 + 0.7 + 2.20705
R1 = 34.9 K
R2 = 18.6 K
34.9 R2
= 12.12
34.9 + R2
6.37
dc load line
5
ϭ 4.55 mA
1 ϩ 0.1
AC load line
Ϫ1
Slope ϭ
ICQ 1͉͉1.2
Ϫ1
ϭ
0.545 K
VCEQ 5
For maximum symmetrical swing
ΔiC = I CQ − 0.25
1
ΔvCE = VCEQ − 0.5 and ΔiC = ⋅ | ΔvCE |
0.545 kΩ
VCEQ − 0.5
I CQ − 0.25 =
0.545
VCEQ = 5 − I CQ (1.1)
0.545 ( I CQ − 0.25 ) = ⎡5 − I CQ (1.1) ⎤ − 0.5
⎣ ⎦
( 0.545 + 1.1) I CQ = 5 − 0.5 + 0.136
I CQ = 2.82 mA, I BQ = 0.0157 mA
RTH = R1 R2 = ( 0.1)(1 + β ) RE
= ( 0.1)(181)( 0.1) = 1.81 kΩ
1
VTH = ⋅ RTH ⋅ V + = I BQ RTH + VBE ( on ) + (1 + β ) I BQ RE
R1

25. 1
(1.81)( 5 ) = ( 0.0157 )(1.81) + 0.7 + (181)( 0.0157 )( 0.1)
R1
1
( 9.05 ) = 1.013 ⇒ R1 = 8.93 kΩ
R1
8.93R2
= 1.81 ⇒ R2 =2.27 kΩ
8.93 + R2
6.38
I CQ = 0.647 mA , VCEQ > 10 − ( 0.647 )( 9 ) = 4.18 V
DiC = I CQ = 0.647 mA
So DvCE = DiC ( 4} 4 ) = ( 0.647 )( 2 ) = 1.294 V
Voltage swing is well within the voltage specification. Then DvCE = 2 (1.294 ) = 2.59 V peak-to-peak
6.39
a.
RTH = R1} R2 = 10}10 = 5 kΩ
⎛ R2 ⎞ ⎛ 10 ⎞
VTH = ⎜ ⎟ (18 ) − 9 = ⎜ ⎟ (18 ) − 9 = 0
⎝ R1 + R2 ⎠ ⎝ 10 + 10 ⎠
0 − 0.7 − ( −9 )
I BQ = = 0.0869 mA
5 + (181)( 0.5 )
I CQ = 15.6 mA, I EQ = 15.7 mA
VCEQ = 18 − (15.7 )( 0.5 ) ⇒ VCEQ = 10.1 V
b.
AC load line
Ϫ1
Slope ϭ
0.5͉͉0.3
Ϫ1
15.6 ϭ
0.188 K
10.1 18
c.
(180 )( 0.026 )
rπ = = 0.30 kΩ
15.6
(1 + β )( RE RL ) ⎛ R1 R2 Rib ⎞
Av = ⋅⎜ ⎟
rπ + (1 + β ) ( RE RL ) ⎝ R1 R2 Rib + RS ⎠
Rib = rπ + (1 + β )( RE RL ) = 0.30 + (181)( 0.5 0.3) or Rib = 34.2 k Ω
R1 R2 Rib = 5 34.2 = 4.36 k Ω
(181)( 0.5 0.3) ⎛ 4.36 ⎞
Av = ⋅⎜ ⎟ ⇒ Av = 0.806
0.3 + (181)( 0.5 0.3) ⎝ 4.36 + 1 ⎠
d.

26. Rib = rp + (1 + b ) ( RE } RL )
Rib = 0.30 + (181)( 0.188 ) ⇒ Rib = 34.3 kΩ
rp + R1} R2 } RS 0.3 + 5}1
Ro = RE = 0.5 ⇒ Ro = 6.18 Ω
1+ b 181
6.40
a.
RTH = R1} R2 = 10}10 = 5 kΩ
⎛ R2 ⎞
VTH = ⎜ ⎟ ( −10 ) = 2 5 V
⎝ R1 + R2 ⎠
VTH = I BQ RTH + VBE ( on ) + (1 + b ) I BQ RE − 10
2 5 − 0.7 − ( −10 )
I BQ = = 0.0174 mA
5 + (121)( 2 )
I CQ = 2.09 mA, I EQ = 2.11 mA
VCEQ = 10 − ( 2.09 )(1) − ( 2.11)( 2 ) ⇒ VCEQ = 3.69 V
b.
AC load line
Ϫ1
Slope ϭ
2͉͉2
Ϫ1
2.09 ϭ
1K
3.69 10
c.
(120 )( 0.026 )
rπ = = 1.49 kΩ
2.09
(1 + β ) ( RE RL ) ⎛ R1 R2 Rib ⎞
Av = ⋅⎜ ⎟
rπ + (1 + β ) ( RE RL ) ⎜ R1 R2 Rib + RS ⎟
⎝ ⎠
Rib = rπ + (1 + β ) ( RE RL ) = 1.49 + (121) ( 2 2)
Rib = 122.5 k Ω, R1 R2 Rib = 5 122.5 = 4.80 k Ω
(121) ( 2 2) ⎛ 4.80 ⎞
Av = ⋅⎜ ⎟ ⇒ Av = 0.484
1.49 + (121) ( 2 2) ⎝ 4.80 + 5 ⎠
d.
Rib = rπ + (1 + b ) ( RE } RL )
Rib = 1.49 + (121) ( 2} 2 ) 1 Rib = 122 kΩ
rπ + R1} R2 } RS 1.49 + 5}5
Ro = RE =2 1 Ro = 32.4 Ω
1+ b 121
6.41
a.

27. RTH = R1 R2 = 60 40 = 24 kΩ
⎛ R2 ⎞ ⎛ 40 ⎞
VTH = ⎜ ⎟ VCC = ⎜ ⎟ ( 5) = 2 V
⎝ R1 + R2 ⎠ ⎝ 40 + 60 ⎠
5 − 0.7 − 2
I BQ = = 0.0130 mA
24 + ( 51)( 3)
I CQ = 0.650 mA, I EQ = 0.663 mA
VECQ = 5 − I EQ RE = 5 − ( 0.663)(3) ⇒ VECQ = 3.01 V
b.
1.63
AC load line
Ϫ1
Slope ϭ 51
Θ 50 Ι Θ3͉͉4Ι
0.65 Ϫ1
ϭ
1.75 K
3.01 5
c.
( 50 )( 0.026 ) 80
rπ = = 2 kΩ, r0 = = 123 kΩ
0.650 0.65
′
Define RL = RE RL r0 = 3 4 123 = 1.69 kΩ
(1 + β ) RL
′ ( 51)(1.69 )
Av = = ⇒ Av = 0.977
rπ (1 + β ) RL′ 2 + ( 51)(1.69 )
⎛ RE r0 ⎞
Ai = (1 + β ) I b ⎜ ⎟
⎜R r +R ⎟
⎝ E 0 L ⎠
⎛ RTH ⎞
Ib = I S ⎜ ⎟
⎝ RTH + Rib ⎠
Rib = rπ + (1 + β ) RL = 2 + ( 51)(1.69 ) = 88.2
′
RE r0 = 3 r0 = 3 123 = 2.93
⎛ 2.93 ⎞ ⎛ 24 ⎞
Ai = ( 51) ⎜ ⎟⎜ ⎟ ⇒ Ai = 4.61
⎝ 2.93 + 4 ⎠ ⎝ 24 + 88.2 ⎠
d.
Rib = rπ + (1 + β ) RE RL r0 = 2 + ( 51)(1.69 ) ⇒ Rib = 88.2 kΩ
rπ ⎛ 2⎞
R0 = RE = ⎜ ⎟ 3 = 0.0392 3
1+ β ⎝ 51 ⎠
R0 = 38.7 Ω
e. Assume variations in rπ and r0 have negligible effects
R1 = 60 ± 5% R1 = 63 kΩ, R1 = 57 kΩ
R2 = 40 ± 5% R2 = 42 kΩ, R2 = 38 kΩ
RE = 3 ± 5% RE = 3.15 kΩ, RE = 2.85 kΩ
RL = 4 ± 5% RL = 4.2 kΩ, RL = 3.8 kΩ

28. ⎛ RE r0 ⎞ ⎛ RTH ⎞
Ai = (1 + β ) ⎜
⎜ R r + R ⎟⎜ R + R ⎟
⎟
⎝ E 0 L ⎠ ⎝ TH ib ⎠
Rib = rπ + (1 + β ) ( RE RL r0 )
RTH ( max ) = 25.2 kΩ, RTH ( min ) = 22.8 kΩ
Rib ( max ) = 92.5 kΩ, Rib ( min ) = 84.0 kΩ
RE ( max ) , RL ( min ) , Rib = 88.6 kΩ
RE ( min ) , RL ( max ) , Rib = 87.4 kΩ
RE ( max ) r0 = 3.07 kΩ
RE ( min ) r0 = 2.79 kΩ
For RE ( min ) , RL ( max ) , RTH ( min )
⎛ 2.79 ⎞ ⎛ 22.8 ⎞
Ai = ( 51) ⎜ ⎟⎜ ⎟ ⇒ Ai = 4.21
⎝ 2.79 + 4.2 ⎠ ⎝ 22.8 + 87.4 ⎠
For RE ( max ) , RL ( min ) , RTH ( max )
⎛ 3.07 ⎞⎛ 25.2 ⎞
Ai = ( 51) ⎜ ⎟⎜ ⎟ ⇒ Ai = 5.05
⎝ 3.07 + 3.8 ⎠⎝ 25.2 + 88.6 ⎠
6.42
(a)
0.5
I BQ = = 0.00617 mA
81
VB = I BQ RB = ( 0.00617 )(10 ) ⇒ VB = 0.0617 V
VE = VB + 0.7 ⇒ VE = 0.7617 V
(b)
⎛ 80 ⎞
I CQ = ( 0.5 ) ⎜ ⎟ = 0.494 mA
⎝ 81 ⎠
I CQ 0.494
gm = = ⇒ g m = 19 mA / V
VT 0.026
β VT (80 )( 0.026 )
rπ = = ⇒ rπ = 4.21 k Ω
I CQ 0.494
VA 150
ro = = ⇒ ro = 304 k Ω
I CQ 0.494
(c)
RS VЈ
S
Ϫ
IS
Vs ϩ RB V␲ r␲ ro
Ϫ
gmV␲
ϩ
Vo
RL
Io
For RS = 0
⎛V ⎞
Vo = − ⎜ π + g mVπ ⎟ ( RL ro )
⎝ rπ ⎠

29. −Vo
so that Vπ =
⎛1+ β ⎞
⎜ ⎟ ( RL ro )
⎝ rπ ⎠
Now Vs + Vπ = Vo
Vo
or Vs = Vo − Vπ = Vo +
⎛ 1+ β ⎞
⎜ ⎟ ( RL ro )
⎝ rπ ⎠
We find
Vo (1 + β )( RL ro ) (81)( 0.5 304 )
Av = = =
Vs rπ + (1 + β )( RL ro ) 4.21 + ( 81)( 0.5 304 )
(81)( 0.5 )
≅ ⇒ Av = 0.906
4.21 + ( 81)( 0.5 )
Rib = rπ + (1 + β )( RL ro ) ≅ 4.21 + ( 81)( 0.5 ) = 44.7 k Ω
⎛ RB ⎞ ⎛ ro ⎞
Ib = ⎜ ⎟ ⋅ I s and I o = ⎜ ⎟ (1 + β ) I b
⎝ RB + Rib ⎠ ⎝ ro + RL ⎠
Then
Io ⎛ RB ⎞⎛ ro ⎞
Ai = = (1 + β ) ⎜ ⎟⎜ ⎟
Is ⎝ RB + Rib ⎠⎝ ro + RL ⎠
⎛ 10 ⎞
Ai ≅ ( 81) ⎜ ⎟ (1) ⇒ Ai = 14.8
⎝ 10 + 44.7 ⎠
(d)
⎛ RB + Rib ⎞ ⎛ 10 44.7 ⎞
⎜ R R + R ⎟ s ⎜ 10 44.7 + 2 ⎟ s (
Vs′ = ⎜ ⋅V = ⋅ V = 0.803) Vs
⎟ ⎜ ⎟
⎝ B ib s ⎠ ⎝ ⎠
Then Av = ( 0.803)( 0.906 ) ⇒ Av = 0.728
Ai = 14.8 (Unchanged)
6.43
(a)
(100 )( 0.026 )
I CQ = 1.98 mA rπ = = 1.313 K
1.98
VA 100
ro = =
I CQ 1.98
= 50.5 K
rπ + RS 1.31 + 10
Ro = ro = 50.5 ⇒ Ro = 112 Ω
1+ β 101
0.112 50.5 ⇒ Ro ≅ 112 Ω
(b) From Equation 4.68
(1 + β ) ( ro RL ) 100
Av = ro = = 50.5 K
rπ + (1 + β ) ( ro RL ) 1.98
(i)

30. RL = 0.5 K
(101) ( 50.5 0.5)
Av =
1.31 + (101) ( 50.5 0.5 )
(101)( 0.4951)
Av = ⇒ Av = 0.974
1.31 + (101)( 0.4951)
(ii)
RL = 5 K ro RL = 50.5 5 = 4.5495
(101)( 4.55)
Av = ⇒ Av = 0.997
1.31 + (101)( 4.55 )
6.44
5 − 0.7
I EQ = = 1.303 I CQ = 1.293 mA
3.3
(125 )( 0.026 )
rπ = = 2.51 K
1.293
1.293
gm = = 49.73 mA/V
0.026
(a)
Rib = rπ + (1 + β ) ( RE RL ) = 2.51 + (126 ) ( 3.3 1)
Rib = 99.2 K
rπ 2.51
Ro = RE = 3.3 = 3.3 0.01992
1+ β 126
Ro = 19.8 Ω
(b)
v 2sin ω t
is = s = ⇒ is ( t ) = 20.2sin ω t ( μ A )
Rib 99.2
veb ( t ) = −is ( t ) rπ = ( −20.2 )( 2.51) sin ω t
veb ( t ) = −50.6sin ω t ( mV )
(1 + β ) ( RE RL ) (126 ) ( 3.3 1) (126 )( 0.7674 )
Av = = =
rπ + (1 + β ) ( RE RL ) 2.51 + (126 ) ( 3.3 1) 2.51 + (126 )( 0.7674 )
Av = 0.9747 ⇒ vo ( t ) = 1.95sin ω t ( V )
v (t )
io ( t ) = o ⇒ io ( t ) = 1.95sin ω t ( mA )
RL
6.45
a.
I EQ = 1 mA , VCEQ = VCC − I EQ RE
5 = 10 − (1)( RE ) ⇒ RE = 5 kΩ
1
I BQ = = 0.0099 mA
101
10 = I BQ RB + VBE ( on ) + I EQ RE
10 = ( 0.0099 ) RB + 0.7 + (1)( 5 ) ⇒ RB = 434 kΩ
b.

31. ␯b
␯0
RB
RE
(100 )( 0.026 )
rπ = = 2.63 kΩ
0.99
v0 (1 + β ) RE(101)( 5 )
= = = 0.995
vb rπ + (1 + β ) RE 2.63 + (101)( 5 )
v0 4
⇒ vb = = ⇒ vb = 4.02 V peak-to-peak at base
0.995 0.995
RS
␯b
ϩ
␯S RB͉͉Rib
Ϫ
Rib = rπ + (1 + β ) RE = 508 kΩ
RB Rib = 434 508 = 234 kΩ
RB Rib 234vS 234
vb = ⋅ vS = = vS
RB Rib + RS 234 + 0.7 234.7
4.02
vb = 0.997vS ⇒ vS = ⇒ vS = 4.03 V peak-to-peak
0.997
c.
Rib = rπ + (1 + β ) ( RE RL )
Rib = 2.63 + (101) ( 5 1) = 86.8 kΩ
RB Rib = 434 86.8 = 72.3 kΩ
⎛ 72.3 ⎞
vb = ⎜ ⎟ vS = 0.99vS = ( 0.99 )( 4.03)
⎝ 72.3 + 0.7 ⎠
vb = 3.99 V peak-to-peak
(1 + β )( RE RL )
v0 = ⋅ vb
rπ + (1 + β )( RE RL )
(101)( 0.833)
= ( 3.99 )
2.63 + (101)( 0.833)
v0 = 3.87 V peak-to-peak
6.46

32. RTH = R1 R2 = 40 60 = 24 kΩ
⎛ 60 ⎞
VTH = ⎜ ⎟ (10 ) = 6 V
⎝ 60 + 40 ⎠
6 − 0.7
β = 75 I BQ = = 0.0131 mA
24 + ( 76 )( 5 )
I CQ = 0.984 mA
6 − 0.7
β = 150 I BQ = = 0.00680 mA
24 + (151)( 5 )
I CQ = 1.02 mA
( 75 )( 0.026 )
β = 75 rπ = = 1.98 kΩ
0.984
β = 150 rπ = 3.82 kΩ
β = 75 Rib = rπ + (1 + β )( RE RL ) = 65.3 kΩ
β = 150 Rib = 130 kΩ
(1 + β )( RE RL ) R1 R2 Rib
Av = ⋅
rπ + (1 + β )( RE RL ) R1 R2 Rib + RS
For β = 75, R1 R2 Rib = 40 60 65.3 = 17.5 k Ω
( 76 )( 0.833) 17.5
Av = ⋅ ⇒ Av = 0.789
1.98 + ( 76 )( 0.833) 17.5 + 4
For β = 150, R1 R2 Rib = 40 60 130 = 20.3 k Ω
(151)( 0.833) 20.3
Av = ⋅ ⇒ Av = 0.811
3.82 + (151)( 0.833) 20.3 + 4
So 0.789 ≤ Av ≤ 0.811
⎛ RE ⎞ ⎛ RTH ⎞
Ai = (1 + β ) ⎜ ⎟⎜ ⎟
⎝ RE + RL ⎠ ⎝ RTH + Rib ⎠
β = 75
⎛ 5 ⎞⎛ 24 ⎞
Ai = ( 76 ) ⎜ ⎟⎜ ⎟ ⇒ Ai = 17.0
⎝ 5 + 1 ⎠ ⎝ 24 + 65.3 ⎠
β = 150
⎛ 5 ⎞ ⎛ 24 ⎞
Ai = (151) ⎜ ⎟ ⎜ ⎟ ⇒ Ai = 19.6
⎝ 6 ⎠ ⎝ 24 + 130 ⎠
17.0 ≤ Ai ≤ 19.6
6.47
(a)

33. ⎛ I ⎞
9 = ⎜ E ⎟ (100 ) + VBE ( on ) + I E RE
⎝ 1+ β ⎠
9 − 0.7
IE =
⎛ 100 ⎞
⎜ ⎟ + RE
⎝ 1+ β ⎠
8.3
β = 50 I E = = 2.803 mA
⎛ 100 ⎞
⎜ ⎟ +1
⎝ 51 ⎠
8.3
β = 200 I E = = 5.543 mA
⎛ 100 ⎞
⎜ ⎟ +1
⎝ 201 ⎠
2.80 ≤ I E ≤ 5.54 mA
VE = I E RE , β = 50, VE = 2.80 V
β = 200, VE = 5.54 V
(b) β = 50, I CQ = 2.748 mA, rπ = 0.473 K
β = 200, I CQ = 5.515 mA, rπ = 0.943 K
Ri = RB ⎡ rπ + (1 + β ) RE
⎣ RL ⎤
⎦
β = 50 ⇒ Ri = 100 ⎡ 0.473 + ( 51)(1 1) ⎤ = 100 25.97 = 20.6 K
⎣ ⎦
β = 200 ⇒ Ri = 100 ⎡0.943 + ( 201)(1 1) ⎤ = 100 101.4 = 50.3 K
⎣ ⎦
From Fig. (4.68)
(1 + β ) ( RE RL ) ⎛ Ri ⎞
Av = ⋅⎜ ⎟
rπ + (1 + β ) ( RE RL ) ⎝ Ri + RS ⎠
( 51) (1 1) ⎛ 20.6 ⎞
= ⋅⎜ ⎟
0.473 + ( 51) (1 1) ⎝ 20.6 + 10 ⎠
β = 50 ⇒ Av = 0.661
( 201) (1 1) ⎛ 50.3 ⎞
β = 200 ⇒ Av = ⎜ ⎟
0.943 + ( 201) (1 1) ⎝ 50.3 + 10 ⎠
Av = 0.826
6.48
Vo = (1 + β ) I b RL
Vs
Ib =
rπ + (1 + β ) RL
(1 + β ) RL
so Av =
rπ + (1 + β ) RL
For β = 100, RL = 0.5 k Ω
(100 )( 0.026 )
rπ = = 5.2 k Ω
0.5

34. (101)( 0.5 )
Then Av ( min ) = = 0.9066
5.2 + (101)( 0.5 )
Then β = 180, RL = 500 k Ω
(180 )( 0.026 )
rπ = = 9.36 k Ω
0.5
(181)( 500 )
Then Av ( max ) = = 0.9999
9.36 + (181)( 500 )
6.49
Rib
IS Ib ϩ
V␲ r␲ gmV␲ ϭ ␤Ib
Ϫ
␯S ϩ R1͉͉R2
Ϫ
RE RL
I0
⎛ RE ⎞
I 0 = (1+ β ) I b ⎜ ⎟
⎝ RE + RL ⎠
⎛ R1 R2 ⎞
Ib = I S ⎜ ⎟
⎝ R1 R2 + Rib ⎠
Rib = rπ + (1 + β )( RE RL )
VCC = 10 V, For VCEQ = 5 V
⎛1+ β ⎞
5 = 10 − ⎜ ⎟ I CQ RE
⎝ β ⎠
β = 80, For RE = 0.5 kΩ
I CQ = 9.88 mA, I EQ = 10 mA, I BQ = 0.123 mA
(80 )( 0.026 )
rπ = = 0.211 kΩ
9.88
Rib = 0.211 + ( 81)( 0.5 0.5 ) ⇒ Rib = 20.46 kΩ
I0 ⎛ RE ⎞ ⎛ R1 R2 ⎞
Ai = = (1 + β ) ⎜ ⎟⎜ ⎟
IS ⎝ RE + RL ⎠⎝ R1 R2 + Rib ⎠
⎛ 1 ⎞⎛ R1 R2 ⎞
8 = ( 81) ⎜ ⎟ ⎜ ⎟
⎝ 2 ⎠ ⎝ R1 R2 + 20.46 ⎠
0.1975 ⎡ R1} R2 + 20.46 ⎤ = R1} R2
⎣ ⎦
R1} R2 ⇒ 5.04 kΩ

35. VTH = I BQ RTH + VBE ( on ) + (1 + b ) I BQ RE
1
( 5.04 )(10 ) = ( 0.123)( 5.04 ) + 0.7 + (10 )( 0.5 ) ⇒ R1 = 7.97 kΩ
R1
7.97 R2
= 5.04 ⇒ R2 = 13.7 kΩ
7.97 + R2
rπ 0.211
Now Ro = RE = 0.5 or Ro = 2.59 Ω
1+ b 81
(b)
Rib = 0.211 + (81) ( 0.5 2) = 32.6 k Ω
⎛ 0.5 ⎞ ⎛ 5.04 ⎞
Ai = ( 81) ⎜ ⎟⎜ ⎟ = ( 81)( 0.2 )( 0.134 )
⎝ 0.5 + 2 ⎠ ⎝ 5.04 + 32.6 ⎠
Ai = 2.17
6.50
Ri = RTH Rib where Rib = rπ + (1 + β ) RE
5 − 3.5
VCEQ = 3.5, I CQ = 0.75 mA
2
(120 )( 0.026 )
rπ = = 4.16 k Ω
0.75
Rib = 4.16 + (121) ( 2 ) = 246 k Ω
Then Ri = 120 = RTH 246 ⇒ RTH = 234 k Ω
0.75
I BQ = = 0.00625 mA
120
VTH = I BQ RTH + VBE ( on ) + (1+ β ) I BQ RE
1 1
⋅ RTH ⋅ VCC = ( 234)(5) = ( 0.00625) ( 234) + 0.7 + (121)( 0.00625 )( 2 )
R1 R1
which yields R1 = 318 k Ω and R2 = 886 k Ω
6.51
a.
12
Let RE = 24 Ω and VCEQ = 1 VCC = 12 V ⇒ I EQ = = 0.5 A
2 24
I CQ = 0.493 A, I BQ = 6.58 mA
( 75)( 0.026 )
rπ = = 3.96 Ω
0.493
Reb
Is Ib ϩ
V␲ r␲ gmV␲ ϭ ␤Ib
Ϫ
VS ϩ R1 ͉͉ R2
Ϫ
ϭ Rrn
RE RL
Io

36. ⎛ RE ⎞
I 0 = (1 + β ) I b ⎜ ⎟
⎝ RE + RL ⎠
⎛ RTH ⎞
Ib = I S ⎜ ⎟
⎝ RTH + Rib ⎠
Rib = rπ + (1 + β ) ( RE RL )
= 3.96 + ( 76 )( 24 8 ) ⇒ Rib = 460 Ω
I0 ⎛ RE ⎞ ⎛ RTH ⎞
Ai = = (1 + β ) ⎜ ⎟⎜ ⎟
IS ⎝ RE + RL ⎠ ⎝ RTH + Rib ⎠
⎛ 24 ⎞ ⎛ RTH ⎞
8 = ( 76) ⎜ ⎟⎜ ⎟
⎝ 24 + 8 ⎠ ⎝ RTH + 460 ⎠
RTH
0.140 = ⇒ RTH = 74.9 Ω (Minimum value)
RTH + 460
dc analysis:
1
VTH = ⋅ RTH ⋅ VCC
R1
= I BQ RTH + VBE ( on ) + I EQ RE
1
( 74.9 )( 24 ) = ( 0.00658)( 74.9 ) + 0.70 + ( 0.5 )( 24 )
R1
= 13.19
136 R2
R1 = 136 Ω, = 74.9 ⇒ R2 = 167 Ω
136 + R2
b.
AC load line
Ϫ1
Slope ϭ
24͉͉8
Ϫ1
0.493 ϭ
6⍀
12 24
1
ΔiC = − Δvce
6
For ΔiC = 0.493 ⇒ Δvce = ( 0.493)( 6 ) ⇒ Max. swing in output voltage for this design
= 5.92 V peak-to-peak
c.
rπ 3.96
R0 = RE = 24 = 0.0521 24 ⇒ R0 = 52 mΩ
1+ β 76
6.52
The output of the emitter follower is
⎛ RL ⎞
vo = ⎜ ⎟ ⋅ vTH
⎝ RL + Ro ⎠

37. Ro
ϩ
␯TH ϩ
␯O RL
Ϫ
Ϫ
For vO to be within 5% for a range of RL , we have
RL ( min ) RL ( max )
= ( 0.95 )
RL ( min ) + Ro RL ( max ) + Ro
4 10
= ( 0.95 ) which yields Ro = 0.364 k Ω
4 + Ro 10 + Ro
⎛ r + R1 R2 RS ⎞
We have Ro = ⎜ π ⎟ RE ro
⎝ 1+ β ⎠
The first term dominates
Let R1 R2 RS ≅ RS , then
rπ + RS r +4
Ro ≅ ⇒ 0.364 = π
1+ β 1+ β
rπ 4 β VT 4
or 0.364 = + = +
1 + β 1 + β I CQ (1 + β ) 1 + β
VT 4
0.364 ≅ +
I CQ 1 + β
4 4 4 V
The factor is in the range of = 0.044 to = 0.0305. We can set Ro ≅ 0.32 = T
1+ β 91 131 I CQ
Or I CQ = 0.08125 mA. To take into account other factors, set I CQ = 0.15 mA,
0.15
I BQ = = 0.00136 mA
110
5
For VCEQ ≅ 5 V , set RE = = 33.3 k Ω
0.15
Design a bias stable circuit.
⎛ R2 ⎞ 1
VTH = ⎜ ⎟ (10) − 5 = ( RTH )(10) − 5
⎝ R1 + R2 ⎠ R1
RTH = ( 0.1)(1 + β ) RE = ( 0.1)(111)(33.3) = 370 k Ω
VTH = I BQ RTH + VBE ( on ) + (1 + β ) I BQ RE − 5
1
So ( 370 )(10 ) − 5 = ( 0.00136 )( 370 ) + 0.7 + (111)( 0.00136 )( 33.3) − 5
R
1
which yields R1 = 594 k Ω and R2 = 981 k Ω
(1 + β ) ( RE RL ) ⎛ RTH Rib ⎞
Now Av = ⋅⎜ ⎟
rπ + (1 + β ) ( RE RL ) ⎝ RTH Rib + RS ⎠
β VT
Rib = rπ + (1 + β ) ( RE RL ) and rπ =
I CQ
For β = 90, RL = 4 k Ω,
rπ = 15.6 k Ω, Rib = 340.6 k Ω
( 91)( 33.3 4 ) 370 340.6
Av = ⋅ ⇒ Av = 0.9332
15.6 + ( 91)( 33.3 4 ) 370 340.6 + 4

38. For β = 90, RL = 10 k Ω
Rib = 715.4 k Ω
( 91)( 33.3 10 ) 370 715.4
Av = ⋅ ⇒ Av = 0.9625
15.6 + ( 91)( 33.3 10 ) 370 715.4 + 4
For β = 130, RL = 4 k Ω
rπ = 22.5 k Ω, Rib = 490 k Ω
(131)( 33.3 4 ) 370 490
Av = ⋅ ⇒ Av = 0.9360
22.5 + (131)( 33.3 4 ) 370 490 + 4
For β = 130, RL = 10 k Ω
Rib = 1030 k Ω
(131)( 33.3 10 ) 370 1030
Av = ⋅ ⇒ Av = 0.9645
22.5 + (131)( 33.3 10 ) 370 1030 + 4
Now vO ( min ) = Av ( min ) .vS = 3.73sin ω t
vO ( max ) = Av ( max ) .vS = 3.86sin ω t
ΔvO
= 3.5%
vO
6.53
PAVG = iL ( rms ) RL ⇒ 1 = iL ( rms )(12 )
2 2
so iL ( rms ) = 0.289 A ⇒ iL ( peak ) = 2 ( 0.289 )
iL ( peak ) = 0.409 A
vL ( peak ) = iL ( peak ) ⋅ RL = ( 0.409 )(12 ) = 4.91 V
4.91
Need a gain of = 0.982
5
With RS = 10 k Ω, we will not be able to meet this voltage gain requirement. Need to insert a buffer or an
op-amp voltage follower (see Chapter 9) between RS and CC1 .
1
Set I EQ = 0.5 A, VCEQ = (12 − ( −12 ) ) = 8 V
3
24 = I EQ RE + VCEQ = ( 0.5 ) RE + 8 ⇒ RE = 32 Ω
50
Let β = 50, I CQ = ( 0.5 ) = 0.49 A
51
β VT ( 50 )( 0.026 )
rπ = = = 2.65 Ω
I CQ 0.49
Rib = rπ + (1 + β ) ( RE RL ) = 2.65 + ( 51) ( 32 12 )
Rib = 448 Ω
(1 + β ) ( RE RL ) ( 51) ( 32 12 )
Av = = = 0.994
rπ + (1 + β ) ( RE RL ) 2.65 + ( 51) ( 32 12 )
So gain requirement has been met.

39. 0.49
I BQ = = 0.0098 A = 9.8 mA
50
24
Let I R ≅ ≅ 10 I B = 98 mA
R1 + R2
So that R1 + R2 = 245 Ω
R2
VTH = ( 24 ) − 12 = I BQ RTH + VBE ( on ) + I EQ RE − 12
R1 + R2
⎛ R2 ⎞ ( 0.0098) R1 R2
⎜ 245 ⎟ ( 24 ) = 245
+ 0.7 + ( 0.5 )( 32 )
⎝ ⎠
Now R1 = 245 − R2
So we obtain
4 × 10−5 R2 + 0.0882 R2 − 16.7 = 0 which yields R2 = 175 Ω and R1 = 70 Ω
2
6.54
(a)
RTH = R1 R2 = 25.6 10.4 = 7.40 k Ω
⎛ R2 ⎞ ⎛ 10.4 ⎞
VTH = ⎜ ⎟ (VCC ) = ⎜ ⎟ (18 ) = 5.2 V
⎝ R1 + R2 ⎠ ⎝ 10.4 + 25.6 ⎠
VTH = I BQ RTH + VBE ( on ) + (1 + β ) I BQ RE
5.2 − 0.7
I BQ = = 0.0117 mA
7.40 + (126 )( 3)
Then I CQ = 1.46 mA and I EQ = 1.47 mA
VCEQ = VCC − I CQ RC − I EQ RE
VCEQ = 18 − (1.46 )( 4 ) − (1.47 )( 3) ⇒ VCEQ = 7.75 V
(b)
(125) ( 0.026 )
rπ = = 2.23 k Ω
1.46
1.46
gm = = 56.2 mA / V
0.026
Re
Vo
Ie r␲ ␤Ib
Is RS RE RC RL
Ib
RTH

40. rπ + RTH 2.23 + 7.40
Re = = = 0.0764 k Ω
1+ β 126
− ( RS RE ) − (100 3)
Ie = ⋅ Is = ⋅ Is
(R S RE ) + Re (100 3) + 0.0764
or I e = − ( 0.974 ) I s
⎛ β ⎞
Vo = − I c ( RC RL ) = − ⎜ ⎟ I e ( RC RL )
⎝ 1+ β ⎠
Vo ⎛ β ⎞ ⎛ 125 ⎞
Then = −⎜ ⎟ ( −0.974 )( RC RL ) = ⎜ ⎟ ( 0.974 )( 4 4 )
Is ⎝ 1+ β ⎠ ⎝ 126 ⎠
V
Then Rm = o = 1.93 k Ω = 1.93 V / mA
Is
(c)
( ) (
Vs = I s RS R E Re = I s 100 3 0.0764 = I s ( 0.0744 ))
Vs
or I s =
0.0744
V V
which yields o = o ( 0.0744 ) = 1.93
I s Vs
Vo
or Av = = 25.9
Vs
6.55
(a)
β ( RC RL )
Av = , RL = 12 k Ω, β = 100
rπ + R1 R2
Let R1 R2 = 50 k Ω, I CQ = 0.5 mA
VTH = I BQ RTH + VBE ( on ) + (1+ β ) I BQ RE
0.5 (100 )( 0.026 )
I BQ = = 0.005 mA, rπ = = 5.2 k Ω
100 0.5
1 1
⋅ RTH ⋅ VCC = ( 50 )(12 ) = ( 0.005 )( 50 ) + 0.7 + (101)( 0.005 )( 0.5 )
R1 R1
which yields R1 = 500 k Ω
and R2 = 55.6 k Ω
(100 )(12 12 )
Av = = 10.9, Design criterion is met.
5.2 + 50
(b)
I CQ = 0.5 mA, I EQ = 0.505 mA
VCEQ = 12 − ( 0.5)(12) − ( 0.505)( 0.5) ⇒ VCEQ = 5.75 V
0.5
Av = g m ( RC RL ) , g m = = 19.23 mA / V
0.026
Av = (19.23) (12 12 ) ⇒ Av = 115
6.56
a. Emitter current

41. I EQ = I CC = 0.5 mA
0.5
I BQ = = 0.00495 mA
101
VE = I EQ RE = ( 0.5 )(1) ⇒ VE = 0.5 V
VB = VE + VBE ( on ) = 0.5 + 0.7 ⇒ VB = 1.20 V
VC = VB + I BQ RB = 1.20 + ( 0.00495 )(100 ) ⇒ VC = 1.7 V
b.
(100 )( 0.026 )
rπ = = 5.25 kΩ
(100 )( 0.00495 )
(100 )( 0.00495 )
gm = = 19.0 mA/V
0.026
Ri
gmV␲
V0
RS Ϫ
VS ϩ RE V␲ r␲ RB RL
Ϫ
ϩ
gmV␲
RS ͉͉RE Ϫ
΂ ΃
RE ϩ
V Ϫ V␲ r␲
RE ϩ RS S
ϩ
Vo = − g mVπ ( RB RL )
RE Rie
Vπ = − ⋅ VS = − ( 0.4971) VS
RE Rie + RS
Vo = (19 )( 0.4971) VS (100 1)
Av = 9.37
c.
gmV␲
IX Ϫ
VX ϩ
Ϫ RE V␲ r␲
ϩ
VX VX
IX = + − g mVπ , Vπ = −VX
RE rπ
IX 1 1 1
= = + + gm
VX Ri RE rπ
1 1
or Ri = RE rπ = 1 5.253
gm 19
Ri = 0.84 0.05252 ⇒ Ri = 49.4 Ω
6.57
(a) I EQ = 1 mA, I CQ = 0.9917 mA

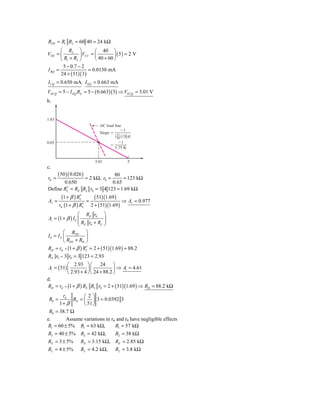
42. VC = 5 − ( 0.9917 )( 2 ) = 3.017 V
VE = −0.7 V
VCEQ = 3.72 V
(b)
Av = g m ( RC RL )
0.9917
gm = = 38.14 mA/V
0.026
Av = ( 38.14 ) ( 2 10 ) ⇒ Av = 63.6
6.58
(a)
10 − 0.7
I EQ = = 0.93 mA
10
I CQ = 0.921 mA
VECQ = 20 − ( 0.93)(10 ) − ( 0.921)( 5 )
VECQ = 6.10 V
(b)
0.921
gm = = 35.42 mA/V
0.026
Av = g m ( RC RL ) = ( 35.42 ) ( 5 50 )
Av = 161
6.59
(a) I EQ = 0.93 mA, I CQ = 0.921 mA
VECQ = 6.10 V
0.921
(b) gm = = 35.42 mA/V rπ = 2.82 K
0.026
From Eq. 6.90
Av = g m
( RC RL ) ⎡ rπ R R ⎤
RS ⎢1 + β E S ⎥
⎣ ⎦
( 35.42 ) ( 50 5 ) ⎡ 2.82 ⎤
= ⎢ 101 10 0.1⎥
0.1 ⎣ ⎦
( 35.42 )( 4.545 )
Av = [0.0218]
0.1
Av = 35.1
6.60
(a)
⎛ 60 ⎞
I CQ = ⎜ ⎟ (1) ⇒ I CQ = 0.984 mA
⎝ 61 ⎠
⎛ 1⎞
VCEQ = I BQ RB + VBE ( on ) = ⎜ ⎟ (100 ) + 0.7
⎝ 61 ⎠
VCEQ = 2.34 V
(b)

43. Av = g m
(RB RL ) ⎡ rπ ⎤
RS ⎥
⎢
RS ⎣1 + β ⎦
0.984
gm = = 37.85 mA/V
0.026
rπ = 1.59 K
( 37.85) (100 2 ) ⎡1.59
⎤
Av = ⎢ 61 0.05⎥
0.05 ⎣ ⎦
= 1484 ⎡ 0.0261 0.05⎤
⎣ ⎦
Av = 25.4
6.61
is ( peak ) = 2.5 mA, Vo ( peak ) = 5 mV
vo 5 × 102 3
So we need Rm = = = 2 × 103 = 2 k Ω
is 2.5 × 102 6
From Problem 4.54
Vo ⎛ β ⎞ ⎛ RS RE ⎞
=⎜ ⎟ ( RC RL ) ⎜
⎜R R +R ⎟ ⎟
Is ⎝ 1+ β ⎠ ⎝ S E ie ⎠
Let RC = 4 k Ω, RL = 5 k Ω, RE = 2 k Ω
Now β = 120, so we have
⎛ 120 ⎞ ⎛ RS RE ⎞ ⎛ RS RE ⎞
2=⎜ ⎟ ( 4 5) ⎜
⎜R R +R ⎟ = 2.204 ⎜
⎟ ⎜R R +R ⎟ ⎟
⎝ 121 ⎠ ⎝ S E ie ⎠ ⎝ S E ie ⎠
RS RE
Then = 0.9075
RS RE + Re
RS RE = 50 2 = 1.923 k Ω, so that Rie = 0.196 k Ω
Assume VCEQ = 3 V
VCC ≅ I CQ ( RC + RE ) + VCEQ
5 = I CQ ( 4 + 2 ) + 3 ⇒ I CQ = 0.333 mA
(120 )( 0.026 )
rπ = = 9.37 k Ω
0.333
r + RTH 9.37 + RTH
Rie = π ⇒ 0.196 =
1+ β 121
which yields RTH = 14.35 k Ω
Now VTH = I BQ RTH + VBE ( on ) + I EQ RE
1 ⎛ 121 ⎞
I BQ = = 0.00833 mA, I EQ = ⎜ ⎟ (1) = 1.008 mA
120 ⎝ 120 ⎠
1 1
VTH = ⋅ RTH ⋅ VCC = (14.35 )( 5 ) = ( 0.00833)(14.35 ) + 0.7 + (1.008 )( 2 )
R1 R1
which yields R1 = 25.3 k Ω
and R2 = 33.2 k Ω
6.62
a.

44. 20 − 0.7
I EQ = = 1.93 mA
10
I CQ = 1.91 mA
VECQ = VCC + VEB ( on ) − I C RC
= 25 + 0.7 − (1.91)( 6.5 ) ⇒ VECQ = 13.3 V
b.
Rie
RS h fe Ib
V0
IS Ie
VS ϩ RE RC RL
Ϫ hie
Ib
Neglect effect hoe
From Problem 6-16, assume
2.45 ≤ hie ≤ 3.7 kΩ
80 ≤ h fe ≤ 120
Vo = ( h fe I b ) ( RC RL )
hie ⎛ RE ⎞
Rie = , Ie = ⎜ ⎟ IS
1 + h fe ⎝ RE + Rie ⎠
⎛ I ⎞ VS
Ib = ⎜ e ⎟ , I S =
⎜ 1+ h ⎟ RS + RE Rie
⎝ fe ⎠
⎛ h fe ⎞ ⎛ RE ⎞ ⎛ 1 ⎞
⎜ 1+ h ⎟( C
Av = ⎜ R RL ) ⎜ ⎟×⎜ ⎟
⎟
⎝ fe ⎠ ⎝ RE + Rie ⎠ ⎝ RS + RE Rie ⎠
High gain device: hie = 3.7 kΩ, h fe = 120
3.7
Rie = = 0.0306 kΩ
121
RE Rie = 10 0.0306 = 0.0305
⎛ 120 ⎞ ⎛ 10 ⎞⎛ 1 ⎞
Av = ⎜ ⎟ ( 6.5 5 ) ⎜ ⎟⎜ ⎟ ⇒ Av = 2.711
⎝ 121 ⎠ ⎝ 10 + 0.0306 ⎠ ⎝ 1 + 0.0305 ⎠
Low gain device: hie = 2.45 kΩ, h fe = 80
2.45
Rie = = 0.03025 kΩ
81
RE Rie = 10 0.03025 = 0.0302
⎛ 80 ⎞ ⎛ 10 ⎞⎛ 1 ⎞
Av = ⎜ ⎟ ( 6.5 5 ) ⎜ ⎟⎜ ⎟ ⇒ Av = 2.70 So Av ≈ constant
⎝ 81 ⎠ ⎝ 10 + 0.03025 ⎠ ⎝ 1 + 0.0302 ⎠
2.70 ≤ Av ≤ 2.71
c.
Ri = RE Rie
We found 0.0302 ≤ Ri ≤ 0.0305 kΩ
Neglecting hoe , Ro = RC = 6.5 kΩ
6.63
a. Small-signal voltage gain

45. Av = g m ( RC RL ) ⇒ 25 = g m ( RC 1)
For VECQ = 3 V ⇒ VC = −VECQ + VEB ( on ) = −3 + 0.7 ⇒ VC = −2.3
5 − 2.3 2.7
VCC − I CQ RC + VC = 0 ⇒ I CQ = = = I CQ
RC RC
For I CQ = 1 mA, RC = 2.7 kΩ
1
gm = = 38.5 mA/V
0.026
Av = ( 38.5 )( 2.7 1) = 28.1
Design criterion satisfied and VECQ satisfied.
⎛ 101 ⎞
IE = ⎜ ⎟ (1) = 1.01 mA
⎝ 100 ⎠
5 − 0.7
VEE = I E RE + VEB ( on ) ⇒ RE = ⇒ RE = 4.26 kΩ
1.01
b.
β VT (100)( 0.026)
rπ = = ⇒ rπ = 2.6 kΩ, g m = 38.5 mA/V, ro = ∞
I CQ 1
6.64
a.
⎛ R2 ⎞ ⎛ 20 ⎞
VTH 1 = ⎜ ⎟ VCC = ⎜ ⎟ (10 ) ⇒ VTH 1 = 2.0 V
⎝ R1 + R2 ⎠ ⎝ 20 + 80 ⎠
RTH 1 = R1 R2 = 20 80 = 16 kΩ
2 − 0.7
I B1 = = 0.0111 mA
16 + (101)(1)
1.11
I C1 = 1.11 mA ⇒ g m1 = ⇒ g m1 = 42.74 mA/V
0.026
(100)( 0.026)
rπ 1 = ⇒ rπ 1 = 2.34 kΩ
1.11
∞
r01 = ⇒ r01 = ∞
1.11
⎛ R4 ⎞ ⎛ 15 ⎞
VTH 2 = ⎜ ⎟ VCC = ⎜ ⎟ (10 ) = 1.50 V
⎝ R3 + R4 ⎠ ⎝ 15 + 85 ⎠
RTH 2 = R3 R4 = 15 85 = 12.75 kΩ
1.50 − 0.70
IB2 = = 0.01265 mA
12.75 + (101)( 0.5 )
1.265
I C 2 = 1.265 mA ⇒ g m 2 = ⇒ g m2 = 48.65 mA/V
0.026
(100 )( 0.026 )
rπ 2 = ⇒ rπ 2 = 2.06 kΩ
1.26
r02 = ∞
b.
Av1 = − g m1 RC1 = − ( 42.7 )( 2 ) ⇒ Av1 = −85.48
Av 2 = − g m 2 ( RC 2 RL ) = − ( 48.5) ( 4 4) ⇒ Av 2 = −97.3
c. Input resistance of 2nd stage

46. Ri 2 = R3 R4 rπ 2 = 15 85 2.06
= 12.75 2.06 ⇒ Ri 2 = 1.773 kΩ
Av′1 = − g m1 ( RC1 Ri 2 ) = − ( 42.7 ) ( 2 1.77B)
Av′1 = −40.17
Overall gain: Av = ( −40.17 )( −97.3) ⇒ Av = 3909
If we had Av1 ⋅ Av 2 = ( −85.48)( −97.3) = 8317
Loading effect reduces overall gain
6.65
a.
⎛ R2 ⎞ ⎛ 12.7 ⎞
VTH 1 = ⎜ ⎟ VCC = ⎜ ⎟ (12) ⇒ VTH 1 = 1.905 V
⎝ R1 + R2 ⎠ ⎝ 12.7 + 67.3 ⎠
RTH 1 = R1 R2 = 12.7 67.3 = 10.68 kΩ
1.905 − 0.70
I B1 = = 0.00477 mA
10.68 + (121)( 2 )
I C1 = 0.572 mA
0.572
g m1 = ⇒ g m1 = 22 mA/V
0.026
(120 )( 0.026 )
rπ 1 = ⇒ rπ 1 = 5.45 kΩ
0.572
∞
r01 = ⇒ r01 = ∞
0.572
⎛ R4 ⎞ ⎛ 45 ⎞
VTH 2 = ⎜ ⎟ VCC = ⎜ ⎟ (12) ⇒ VTH 2 = 9.0 V
⎝ R3 + R4 ⎠ ⎝ 45 + 15 ⎠
RTH 2 = R3 R4 = 15 45 = 11.25 kΩ
9.0 − 0.70
I B2 = = 0.0405 mA
11.25 + (121)(1.6)
I C2 = 4.86 mA
4.86
gm2 = ⇒ g m 2 = 187 mA/V
0.026
(120 )( 0.026 )
rπ 2 = ⇒ rπ 2 = 0.642 kΩ
4.86
r02 = ∞
b.
I E1 = 0.577 mA
VCEQ1 = 12 − ( 0.572 ) (10 ) − ( 0.577 ) ( 2 ) ⇒ VCEQ1 = 5.13 V
I E 2 = 4.90
VCEQ 2 = 12 − ( 4.90 )(1.6 ) ⇒ VCEQ 2 = 4.16 V

47. Q1
AC load line
Ϫ1
Slope ϭ
10͉͉7.92
Ϫ1
ϭ
4.42 K
0.572
5.13 12
Q2
AC load line
Ϫ1
Slope ϭ
1.6͉͉0.25
Ϫ1
4.86 ϭ
0.216 K
4.16 12
Ri 2 = R3 R4 Rib
Rib = rπ 2 + (1 + β ) ( RE 2 RL )
= 0.642 + (121) (1.6 0.25 )
Rib = 26.8
Ri 2 = 15 45 26.8
Ri 2 = 7.92 kΩ
c.
Av1 = − g m1 ( RC1 Ri 2 ) = − ( 22 )(10 7.92 ) ⇒ Av 2 = −97.2
(1 + β )( RE 2 RL )
Av 2 =
rπ 2 + (1 + β )( RE 2 RL )
(121)( 0.216 )
= = 0.976
0.642 + (121)( 0.216 )
Overall gain = ( −97.2 )( 0.976 ) = −94.9
d.
RiS = R1 R2 rπ 1 = 67.3 12.7 5.45 ⇒ RiS = 3.61 kΩ
rπ 2 + RS
Ro = RE 2 where
1+ β
RS = R3 R4 RC1
= 15 45 10 ⇒ RS = 5.29 kΩ
0.642 + 5.29
Ro = 1.6 ⇒ 0.049 1.6 ⇒ Ro = 47.6 Ω
121
e.
−1
ΔiC = ⋅ Δvce , ΔiC = 4.86
0.216 kΩ
Δvce = ( 4.86 )( 0.216 ) = 1.05 V
Max. output voltage swing = 2.10 V peak-to-peak
6.66
(a)

48. 5 − 2 ( 0.7 )
I R1 = = 72 mA
0.050
0.7
IR2 = = 1.4 mA
0.5
⎛ β ⎞
IC 2 =⎜ ⎟ ( 72 − 1.4 ) ⇒ I C 2 = 69.9 mA
⎝ 1+ β ⎠
69.9
IB2 = = 0.699 mA
100
⎛ β ⎞
I C1 =⎜ ⎟ (1.4 + 0.699 ) ⇒ I C1 = 2.08 mA
⎝ 1+ β ⎠
(b)
ϩ
Vs ϩ
Ϫ V␲1 r␲1
gm1V␲1 gm2V␲2
Ϫ
r␲2 ϩ
0.5 k⍀ V␲2
Ϫ
Vo
50 Ω
Vs = Vπ 1 + Vπ 2 + Vo
(1)
⎛V V ⎞
Vo = ⎜ π 2 + π 2 + g m 2Vπ 2 ⎟ ( 0.05 )
⎝ 0.5 rπ 2 ⎠
(100 )( 0.026 )
rπ 2 = = 0.0372 k Ω
69.9
69.9
gm2 = = 2688 mA / V
0.026
⎛ 1 1 ⎞ V
Vo = Vπ 2 ⎜ + + 2688 ⎟ ( 0.05 ) so that (1) Vπ 2 = o
⎝ 0.5 0.0372 ⎠ 135.8
(2)

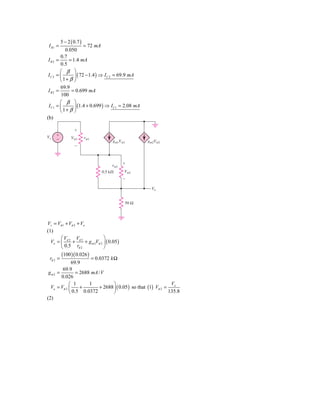
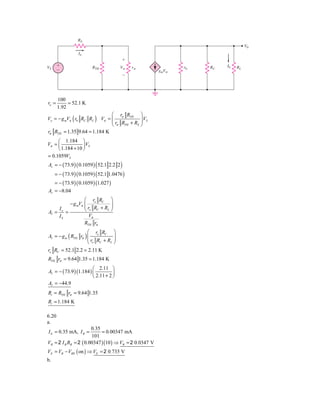
49. Vπ 1 V V
+ g m1Vπ 1 = π 2 + π 2
rπ 1 0.5 rπ 2
(100 )( 0.026 )
rπ 1 = = 1.25 k Ω
2.08
2.08
g m1 = = 80 mA / V
0.026
⎛ 1 ⎞ ⎛ 1 1 ⎞
Vπ 1 ⎜ + 80 ⎟ = Vπ 2 ⎜ + ⎟
⎝ 1.25 ⎠ ⎝ 0.5 0.0372 ⎠
⎛ V ⎞
Vπ 1 ( 80.8 ) = Vπ 2 ( 28.88 ) = ⎜ o ⎟ ( 28.88 ) or (2) Vπ 1 = Vo ( 0.00261)
⎝ 136.7 ⎠
V V
Then Vs = Vo ( 0.00261) + o + Vo = Vo (1.00993) or Av = o = 0.990
136.7 Vs
(c)
Rib = rπ 1 (1 + β ) [ Rx ]
Ix
ϩ
Vx ϩ
Ϫ 0.5 k⍀ V␲2 r␲2
gm2V␲2
Ϫ
Vo
50 ⍀
Vπ 2 Vπ 2 ⎛ 1 1 ⎞
Ix = + = Vπ 2 ⎜ + ⎟
0.5 rπ 2 ⎝ 0.5 rπ 2 ⎠
Vo V − Vπ 2
= x = I x + g m 2Vπ 2
0.05 0.05
⎛ 1 ⎞
Ix ⎜ + gm2 ⎟
Vx ⎛ 1 ⎞ ⎝ 0.05 ⎠
− I x = Vπ 2 ⎜ + gm2 ⎟ =
0.05 ⎝ 0.05 ⎠ ⎛ 1 1 ⎞
⎜ + ⎟
⎝ 0.5 rπ 2 ⎠
Vx
We find = Rx = 4.74 k Ω
Ix
Then Rib = 1.25 + (101) ( 2.89 ) ⇒ Rib = 480 k Ω

50. ϩ
V␲1 r␲1
gm1V␲1 gm2V␲2
Ϫ
r␲2 ϩ
0.5 k⍀ V␲2
Ϫ
Ix
ϩ
50 ⍀ Ϫ
Vx
To find Ro:
Vx V
(1) Ix = − g m 2Vπ 2 − π 2
0.05 0.5 rπ 2
⎛V ⎞ ⎛ 1 ⎞
(2) Vπ 2 = ⎜ π 1 + g m1Vπ 1 ⎟ ( 0.5 rπ 2 ) = Vπ 1 ⎜ + 80 ⎟ ( 0.5 0.0372 ) or Vπ 2 = ( 2.77 ) Vπ 1
⎝ rπ 1 ⎠ ⎝ 1.25 ⎠
(3) Vπ 1 + Vπ 2 + Vx = 0 ⇒ Vπ 1 + ( 2.77 ) Vπ 1 + Vx = 0
so that Vπ 1 = − ( 0.2653) Vx
and Vπ 2 = ( 2.77 ) ⎡ − ( 0.2653) Vx ⎤ = − ( 0.735 ) Vx
⎣ ⎦
Vx ⎛ 1 ⎞
Now I x = − Vπ 2 ⎜ g m 2 + ⎟
0.05 ⎜ 0.5 rπ 2 ⎟
⎝ ⎠
Vx ⎡ 1 ⎤ Vx
So that I x = + ( 0.735 ) Vx ⎢ 2688 + ⎥ which yields Ro = = 0.496 Ω
0.05 ⎢
⎣ 0.5 0.0372 ⎥
⎦ Ix
6.67
a.
RTH = R1 R2 = 335 125 = 91.0 kΩ
⎛ R2 ⎞
VTH = ⎜ ⎟ VCC
⎝ R1 + R2 ⎠
⎛ 125 ⎞
=⎜ ⎟ (10 ) = 2.717 V
⎝ 125 + 335 ⎠
VTH = I B1 RTH + VBE1 + VBE 2 + I E 2 RE 2
I E 2 = (1 + β ) I E1 = (1 + β ) I B1
2
2.717 − 1.40
I B1 = ⇒ I B1 = 0.128 μΑ
91.0 + (101) (1)
2
I C1 = 12.8 μΑ
I C 2 = β I E1 = β (1 + β ) I B1 = (100 )(101)( 0.128 μΑ )
I C 2 = 1.29 mΑ, I E 2 = 1.31 mΑ
I RC = I C 2 + I C1 = 1.29 + 0.0128 = 1.30 mΑ

51. VC = 10 − I RC RC = 10 − (1.30 )( 2.2 ) = 7.14 V
VE = I E 2 RE 2 = (1.30 )(1) = 1.30 V
VCE 2 = 7.14 − 1.30 = 5.84 V
VCE1 = VCE 2 − VBE 2 = 5.84 − 0.7
VCE1 = 5.14 V
Summary:
I C1 = 12.8 μΑ I C 2 = 1.29 mΑ
VCE1 = 5.14 V VCE 2 = 5.84 V
b.
0.0128
g m1 = = 0.492 mΑ / V
0.026
1.292
gm2 = = 49.7 mΑ / V
0.026
Rib
V0
ϩ
Ib
V␲1 r␲1
gm1V␲1
ϩ Ϫ
VS ϩ RC
Ϫ
gm2V␲2
R1͉͉ R2 V␲2 r␲2
Ϫ
V0 = − ( g m1Vπ 1 + g m 2Vπ 2 ) RC
VS = Vπ 1 + Vπ 2 , Vπ 1 = VS − Vπ 2
⎛V ⎞
Vπ 2 = ⎜ π 1 + g m1Vπ 1 ⎟ rπ 2
⎝ rπ 1 ⎠
⎛1+ β ⎞
Vπ 2 = Vπ 1 ⎜ ⎟ rπ 2
⎝ rπ 1 ⎠
V0 = − ⎡ g m1 (VS − Vπ 2 ) + g m 2Vπ 2 ⎤ RC
⎣ ⎦
V0 = − ⎡ g m1VS + ( g m 2 − g m1 ) Vπ 2 ⎤ RC
⎣ ⎦
⎛r ⎞
Vπ 2 = (VS − Vπ 2 )(1 + β ) ⎜ π 2 ⎟
⎝ rπ 1 ⎠
⎡ ⎛ r ⎞⎤ ⎛r ⎞
Vπ 2 ⎢1 + (1 + β ) ⎜ π 2 ⎟ ⎥ = VS (1 + β ) ⎜ π 2 ⎟
⎣ ⎝ rπ 1 ⎠ ⎦ ⎝ rπ 1 ⎠

52. ⎧ ⎛r ⎞⎫
⎪ VS (1 + β ) ⎜ π 2 ⎟ ⎪
⎪
V0 = − ⎨ g m1VS + ( g m 2 − g m1 ) ⋅ ⎝ rπ 1 ⎠ ⎪ R
⎬ C
⎪ ⎛r ⎞
1 + (1 + β ) ⎜ π 2 ⎟ ⎪
⎪ ⎝ rπ 1 ⎠ ⎪
⎩ ⎭
V0
Av =
VS
⎧ 2.01 ⎞ ⎫
⎪ ( 49.7 − 0.492 )(101) ⎛
⎜ ⎟⎪
⎪ ⎝ 203 ⎠ ⎪ 2.2
= − ⎨( 0.492 ) + ⎬
⎪ ⎛ 2.01 ⎞ ⎪
1 + (101) ⎜ ⎟
⎪
⎩ ⎝ 203 ⎠ ⎪
⎭
Av = −55.2
c.
Ris = R1 R2 Rib
Rib = rπ 1 + (1 + β ) rπ 2
= 203 + (101)( 2.01) = 406 kΩ
Ris = 91 406 = 74.3 kΩ = Ris
R0 = RC = 2.2 kΩ
6.68
R0
Ix
ϩ
ϩ Vx
V␲1 r␲1 ro1
Ϫ
gm1V␲1
Ϫ
VA
ϩ
V␲2 r␲2 ro2
gm2V␲2
Ϫ
Vx Vx − VA
(1) I x = g m 2Vπ 2 + + + g m1Vπ 1
ro 2 ro1
Vx − VA VA
(2) + g m1Vπ 1 =
ro1 rπ 1 rπ 2
(3) Vπ 2 = VA = −Vπ 1
Then from (2)
Vx ⎛ 1 1 ⎞
= VA ⎜ + g m1 + ⎟
ro1 ⎜r rπ 1 rπ 2 ⎟
⎝ o1 ⎠
Vx Vx VA ⎛ 1 1 ⎞ ⎛ 1 ⎞
(1) I x = g m 2VA + + − − g m1VA or I x = Vx ⎜ + ⎟ + VA ⎜ g m 2 − − g m1 ⎟
ro 2 ro1 ro1 ⎝ ro1 ro 2 ⎠ ⎝ ro1 ⎠
Solving for VA from Equation (2) and substituting into Equation (1), we find

53. 1 1
+ g m1 +
V ro1 rπ 1 rπ 2
Ro = x =
Ix 1 ⎛ 1 1 ⎞ 1 ⎛ 1 ⎞
⎜ + g m1 + ⎟+ ⎜ + gm2 ⎟
ro 2 ⎝ ro1 rπ 1 rπ 2 ⎠ ro1 ⎝ rπ 1 rπ 2 ⎠
For β = 100, VA = 100 V , I C1 = I Bias = 1 mA
100
ro1 = ro 2 = = 100 k Ω
1
(100 )( 0.026 )
rπ 1 = rπ 2 = = 2.6 k Ω
1
1
g m1 = g m 2 = = 38.46 mA/V
0.026
1 1
+ 38.46 +
100 2.6 2.6
Then Ro =
1 ⎛ 1 1 ⎞ 1 ⎛ 1 ⎞
⎜ + 38.46 + ⎟+ ⎜ + 38.46 ⎟
100 ⎜ 100
⎝ 2.6 2.6 ⎟ 100 ⎜ 2.6 2.6
⎠ ⎝
⎟
⎠
or Ro = 50.0 k Ω
Now I C 2 = 1 mA, I Bias = 0
IC 2 β I
Replace I Bias by ⋅ = C 2 , I C1 ≅ 0.01 mA
β 1+ β 1+ β
100 100
ro 2 = = 100 k Ω, ro1 = = 10, 000 k Ω
1 0.01
1
gm2 = = 38.46 mA/V , g m1 = 0.3846 mA/V
0.026
(100 )( 0.026 )
rπ 2 = = 2.6 k Ω, rπ 1 = 260 k Ω
1
Then Ro = 66.4 k Ω
6.69
a.
RTH = R1 R2 = 93.7 6.3 = 5.90 k Ω
⎛ R2 ⎞
VTH = ⎜ ⎟ VCC
⎝ R1 + R2 ⎠
⎛ 6.3 ⎞
=⎜ ⎟ (12 ) = 0.756 V
⎝ 6.3 + 93.7 ⎠
0.756 − 0.70
I BQ = = 0.00949 mA
5.90
I CQ = 0.949 mA
VCEQ = 12 − ( 0.949 )( 6 ) ⇒ VCEQ = 6.305 V
Transistor:
PQ ≈ I CQVCEQ = ( 0.949 )( 6.305 ) ⇒ PQ = 5.98 mW
RC : PR = I CQ RC = ( 0.949 ) ( 6 ) ⇒ PR = 5.40 mW
2 2
b.

54. 2 AC load line
Ϫ1
Slope ϭ
6͉͉105
Ϫ1
ϭ
0.949 5.68 K
6.31 12
100
r0 = = 105 kΩ
0.949
Peak signal current = 0.949 mA
V0 ( max ) = ( 5.68 )( 0.949 ) = 5.39 V
1 V0 ( max ) 1 ⎡ ( 5.39 ) ⎤
2 2
PRC = ⋅ = ⎢ ⎥ ⇒ PRC = 2.42 mW
2 RC 2⎢ 6 ⎥
⎣ ⎦
6.70
(a)
10 = I BQ RB + VBE ( on ) + (1 + β ) I BQ RE
10 − 0.7
I BQ = = 0.00369 mA
100 + (121)( 20 )
I CQ = 0.443 mA, I EQ = 0.447 mA
For RC : PRC = ( 0.443) (10 ) ⇒ PRC = 1.96 mW
2
For RE : PRE = ( 0.447 ) ( 20 ) ⇒ PRE = 4.0 mW
2
(b)
ΔiC = 0.667 − 0.443 = 0.224 mA
1 1
( ΔiC ) RC = ( 0.224 ) (10 )
2 2
Then P RC =
2 2
P RC = 0.251 mW
6.71
a.
10 − 0.7
I BQ = = 0.00596 mA
50 + (151)(10 )
I CQ = 0.894 mA, I EQ = 0.90 mA
VECQ = 20 − ( 0.894 )( 5 ) − ( 0.90 )(10 ) ⇒ VECQ = 6.53 V
PQ ≅ I CQVECQ = ( 0.894 )( 6.53) ⇒ PQ = 5.84 mW
PRC ≅ I CQ RC = ( 0.894 ) ( 5 ) ⇒ PRC = 4.0 mW
2 2
PRE ≅ I EQ RE = ( 0.90 ) (10 ) ⇒ PRE = 8.1 mW
2 2
b.

55. AC load line
Ϫ1
Slope ϭ
5͉͉2
Ϫ1
ϭ
0.894 1.43 K
6.53 20
−1
ΔiC = ⋅ Δvec
1.43 kΩ
ΔiC = 0.894 ⇒ Δvec = ( 0.894 )(1.43) = 1.28 V
⎛ 5 ⎞
Δi0 = ⎜ ⎟ ΔiC = 0.639 mA
⎝5+2⎠
1
PRL = ( 0.639 ) ( 2 ) ⇒ PRL = 0.408 mW
2
2
1
PRC = ⋅ ( 0.894 − 0.639 ) ( 5 ) ⇒ PRC = 0.163 mW
2
2
PRE = 0
PQ = 5.84 − 0.408 − 0.163 ⇒ PQ = 5.27 mW
6.72
10 − 0.70
I BQ = = 0.00838 mA
100 + (101)(10 )
I CQ = 0.838 mA, I EQ = 0.846 mA
VCEQ = 20 − ( 0.838 )(10 ) − ( 0.846 )(10 ) ⇒ VCEQ = 3.16 V
AC load line
Ϫ1
Slope ϭ
RE ͉͉RL͉͉r0
0.838
3.16 20
100
r0 = = 119 kΩ
0.838
Neglecting base currents:
a.
RL = 1 kΩ
−1 −1
slope = =
10 1 119 0.902 kΩ
−1
ΔiC = ⋅ ΔVce
0.902 kΩ
ΔiC = 0.838 ⇒ ΔVce = ( 0.902 )( 0.838 ) = 0.756 V
1 ( 0.756 )
2
PRL = ⇒ PRL = 0.286 mW
2 1
b.

56. RL = 10 kΩ
−1 −1
slope = =
10 10 119 4.80
For ΔiC = 0.838 ⇒ Δvce = ( 0.838 )( 4.80 ) = 4.02
1 ( 3.16 )
2
Max. swing determined by voltage PRL = ⇒ PRL = 0.499 mW
2 10
6.73
a.
10 − 0.7
I BQ = = 0.00838 mA
100 + (101)(10 )
I CQ = 0.838 mA, I EQ = 0.846 mA
VCEQ = 20 − ( 0.838 )(10 ) − ( 0.846 )(10 ) ⇒ VCEQ = 3.16 V
PQ ≅ I CQVCEQ = ( 0.838 )( 3.16 ) ⇒ PQ = 2.65 mW
PRC ≅ I CQ RC = ( 0.838 ) (10 ) ⇒ PRC = 7.02 mW
2 2
b.
AC load line
Ϫ1
Slope ϭ
RC ͉͉RL
Ϫ1 Ϫ1
0.838 ϭ ϭ
10͉͉1 0.909 K
3.16 20
−1
ΔiC = ⋅ Δvce
0.909 kΩ
For ΔiC = 0.838 ⇒ Δvce = ( 0.909 )( 0.838 ) = 0.762 V
⎛ RC ⎞ ⎛ 10 ⎞
Δi0 = ⎜ ⎟ ΔiC = ⎜ ⎟ ΔiC = 0.762 mA
⎝ RC + RL ⎠ ⎝ 10 + 1 ⎠
1
PRL = ( 0.762 ) (1) ⇒ PRL = 0.290 mW
2
2
1
PRC = ⋅ ( 0.838 − 0.762 ) (10 ) ⇒ PRC = 0.0289 mW
2
2
PQ = 2.65 − 0.290 − 0.0289 ⇒ PQ = 2.33 mW