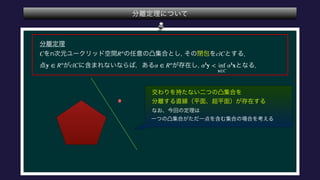
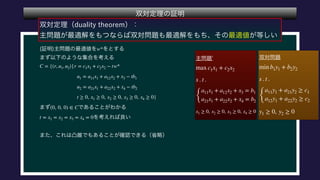
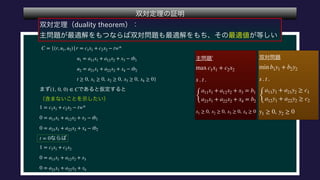
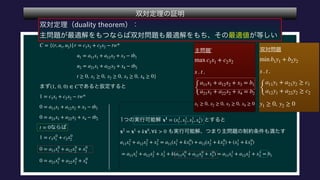
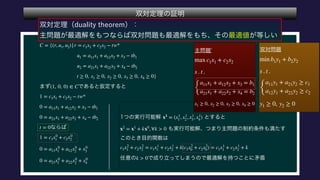
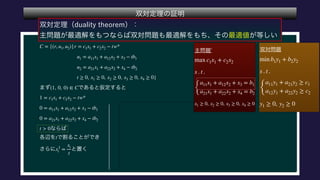
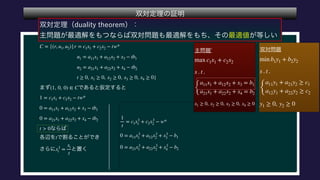
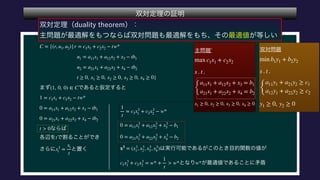
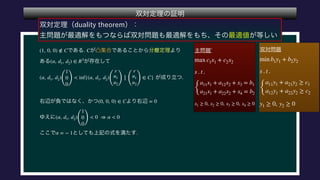
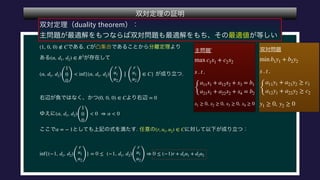
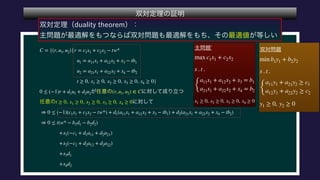
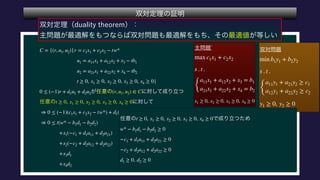
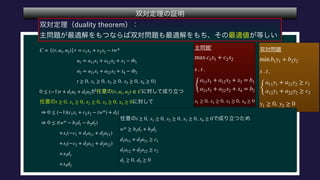
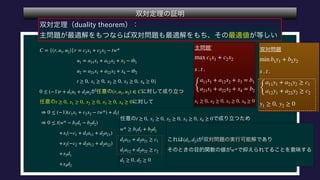
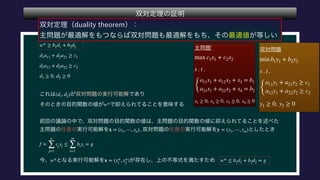
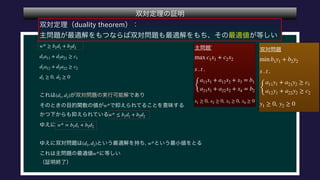
The document describes a set C, defined as a collection of points (r,u1,u2) satisfying certain constraints. It is shown that (1,0,0) does not belong to C by finding values for α, d1, d2 such that αr + d1u1 + d2u2 is always less than 0 for points in C. Specifically, it is shown that for α = -1, this inequality holds. Optimization problems are also described that involve maximizing and minimizing linear functions over C.

1. 5

2. 1.

3. 1.
(a)
(b)
2.
(a)

5.
ℜn
C
∀x ∈ C, ∀α ≥ 0, αx ∈ C
C
ℜn
C
∀x ∈ C, ∀y ∈ C, ∀α ∈ [0,1], αx + (1 − α)y ∈ C
C
C

6.
C Rn
clC
y ∈ Rn
clC α ∈ Rn
αt
y < inf
x∈C
αt
x

8.
w*
C = {(r, u1, u2)|r = c1x1 + c2x2 − tw*
u1 = a11x1 + a12x2 + x3 − tb1
u2 = a21x1 + a22x2 + x4 − tb2
t ≥ 0, x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0}
(0, 0, 0) ∈ C
t = x1 = x2 = x3 = x4 = 0
min b1y1 + b2y2
s . t .
{
a11y1 + a21y2 ≥ c1
a12y1 + a22y2 ≥ c2
y1 ≥ 0, y2 ≥ 0
max c1x1 + c2x2
s . t .
{
a11x1 + a12x2 + x3 = b1
a21x1 + a22x2 + x4 = b2
x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0

9.
w*
C = {(r, u1, u2)|r = c1x1 + c2x2 − tw*
u1 = a11x1 + a12x2 + x3 − tb1
u2 = a21x1 + a22x2 + x4 − tb2
t ≥ 0, x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0}
(1, 0, 0) ∈ C
1 = c1x1 + c2x2 − tw*
0 = a11x1 + a12x2 + x3 − tb1
0 = a21x1 + a22x2 + x4 − tb2
t = 0
1 = c1x1 + c2x2
0 = a11x1 + a12x2 + x3
0 = a21x1 + a22x2 + x4
max c1x1 + c2x2
s . t .
{
a11x1 + a12x2 + x3 = b1
a21x1 + a22x2 + x4 = b2
x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0
min b1y1 + b2y2
s . t .
{
a11y1 + a21y2 ≥ c1
a12y1 + a22y2 ≥ c2
y1 ≥ 0, y2 ≥ 0

10.
C = {(r, u1, u2)|r = c1x1 + c2x2 − tw*
u1 = a11x1 + a12x2 + x3 − tb1
u2 = a21x1 + a22x2 + x4 − tb2
t ≥ 0, x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0}
(1, 0, 0) ∈ C
1 = c1x1 + c2x2 − tw*
0 = a11x1 + a12x2 + x3 − tb1
0 = a21x1 + a22x2 + x4 − tb2
t = 0
1 = c1x0
1 + c2x0
2
0 = a11x0
1 + a12x0
2 + x0
3
0 = a21x0
1 + a22x0
2 + x0
4
x1
= (x1
1, x1
2, x1
3, x1
4)
x2
= x1
+ kx0
, ∀k > 0
a11x2
1 + a12x2
2 + x2
3 = a11(x1
1 + kx0
1) + a12(x1
2 + kx0
2) + (x1
3 + kx0
3)
= a11x1
1 + a12x1
2 + x1
3 + k(a11x0
1 + a12x0
2 + x0
3) = a11x1
1 + a12x1
2 + x1
3 = b1
max c1x1 + c2x2
s . t .
{
a11x1 + a12x2 + x3 = b1
a21x1 + a22x2 + x4 = b2
x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0
min b1y1 + b2y2
s . t .
{
a11y1 + a21y2 ≥ c1
a12y1 + a22y2 ≥ c2
y1 ≥ 0, y2 ≥ 0

11.
C = {(r, u1, u2)|r = c1x1 + c2x2 − tw*
u1 = a11x1 + a12x2 + x3 − tb1
u2 = a21x1 + a22x2 + x4 − tb2
t ≥ 0, x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0}
(1, 0, 0) ∈ C
1 = c1x1 + c2x2 − tw*
0 = a11x1 + a12x2 + x3 − tb1
0 = a21x1 + a22x2 + x4 − tb2
t = 0
1 = c1x0
1 + c2x0
2
0 = a11x0
1 + a12x0
2 + x0
3
0 = a21x0
1 + a22x0
2 + x0
4
x1
= (x1
1, x1
2, x1
3, x1
4)
x2
= x1
+ kx0
, ∀k > 0
c1x2
1 + c2x2
2 = c1x1
1 + c2x1
2 + k(c1x2
0 + c2x2
0) = c1x1
1 + c2x1
2 + k
k > 0
max c1x1 + c2x2
s . t .
{
a11x1 + a12x2 + x3 = b1
a21x1 + a22x2 + x4 = b2
x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0
min b1y1 + b2y2
s . t .
{
a11y1 + a21y2 ≥ c1
a12y1 + a22y2 ≥ c2
y1 ≥ 0, y2 ≥ 0

12.
C = {(r, u1, u2)|r = c1x1 + c2x2 − tw*
u1 = a11x1 + a12x2 + x3 − tb1
u2 = a21x1 + a22x2 + x4 − tb2
t ≥ 0, x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0}
(1, 0, 0) ∈ C
1 = c1x1 + c2x2 − tw*
0 = a11x1 + a12x2 + x3 − tb1
0 = a21x1 + a22x2 + x4 − tb2
t > 0
t
x3
i =
xi
t
max c1x1 + c2x2
s . t .
{
a11x1 + a12x2 + x3 = b1
a21x1 + a22x2 + x4 = b2
x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0
min b1y1 + b2y2
s . t .
{
a11y1 + a21y2 ≥ c1
a12y1 + a22y2 ≥ c2
y1 ≥ 0, y2 ≥ 0

13.
C = {(r, u1, u2)|r = c1x1 + c2x2 − tw*
u1 = a11x1 + a12x2 + x3 − tb1
u2 = a21x1 + a22x2 + x4 − tb2
t ≥ 0, x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0}
(1, 0, 0) ∈ C
1 = c1x1 + c2x2 − tw*
0 = a11x1 + a12x2 + x3 − tb1
0 = a21x1 + a22x2 + x4 − tb2
t > 0
t
x3
i =
xi
t
1
t
= c1x3
1 + c2x3
2 − w*
0 = a11x3
1 + a12x3
2 + x3
3 − b1
0 = a21x3
1 + a22x3
2 + x3
4 − b2
max c1x1 + c2x2
s . t .
{
a11x1 + a12x2 + x3 = b1
a21x1 + a22x2 + x4 = b2
x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0
min b1y1 + b2y2
s . t .
{
a11y1 + a21y2 ≥ c1
a12y1 + a22y2 ≥ c2
y1 ≥ 0, y2 ≥ 0

14.
C = {(r, u1, u2)|r = c1x1 + c2x2 − tw*
u1 = a11x1 + a12x2 + x3 − tb1
u2 = a21x1 + a22x2 + x4 − tb2
t ≥ 0, x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0}
(1, 0, 0) ∈ C
1 = c1x1 + c2x2 − tw*
0 = a11x1 + a12x2 + x3 − tb1
0 = a21x1 + a22x2 + x4 − tb2
t > 0
t
x3
i =
xi
t
1
t
= c1x3
1 + c2x3
2 − w*
0 = a11x3
1 + a12x3
2 + x3
3 − b1
0 = a21x3
1 + a22x3
2 + x3
4 − b2
x3
= (x3
1, x3
2, x3
3, x3
4)
c1x3
1 + c2x3
2 = w* +
1
t
> w* w*
max c1x1 + c2x2
s . t .
{
a11x1 + a12x2 + x3 = b1
a21x1 + a22x2 + x4 = b2
x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0
min b1y1 + b2y2
s . t .
{
a11y1 + a21y2 ≥ c1
a12y1 + a22y2 ≥ c2
y1 ≥ 0, y2 ≥ 0

15.
(1, 0, 0) ∉ C C
(α, d1, d2) ∈ R3
(α, d1, d2)
(
1
0
0)
< inf{(α, d1, d2)
(
r
u1
u2
) (
r
u1
u2
)
∈ C}
(
r
u1
u2
)
∈ C
αr + d1u1 + d2u2 < 0 C k > 0
kr
ku1
ku2
∈ C
α(kr) + d1(ku1) + d2(ku2) < 0
k(αr + d1u1 + d2u2) < α
max c1x1 + c2x2
s . t .
{
a11x1 + a12x2 + x3 = b1
a21x1 + a22x2 + x4 = b2
x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0
min b1y1 + b2y2
s . t .
{
a11y1 + a21y2 ≥ c1
a12y1 + a22y2 ≥ c2
y1 ≥ 0, y2 ≥ 0

16.
(1, 0, 0) ∉ C C
(α, d1, d2) ∈ R3
(α, d1, d2)
(
1
0
0)
< inf{(α, d1, d2)
(
r
u1
u2
) (
r
u1
u2
)
∈ C}
(0, 0, 0) ∈ C = 0
(α, d1, d2)
(
1
0
0)
< 0 ⇒ α < 0
α = − 1
max c1x1 + c2x2
s . t .
{
a11x1 + a12x2 + x3 = b1
a21x1 + a22x2 + x4 = b2
x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0
min b1y1 + b2y2
s . t .
{
a11y1 + a21y2 ≥ c1
a12y1 + a22y2 ≥ c2
y1 ≥ 0, y2 ≥ 0

17.
(1, 0, 0) ∉ C C
(α, d1, d2) ∈ R3
(α, d1, d2)
(
1
0
0)
< inf{(α, d1, d2)
(
r
u1
u2
) (
r
u1
u2
)
∈ C}
(0, 0, 0) ∈ C = 0
(α, d1, d2)
(
1
0
0)
< 0 ⇒ α < 0
α = − 1 (r, u1, u2) ∈ C
inf{(−1, d1, d2)
(
r
u1
u2
)
} = 0 ≤ (−1, d1, d2)
(
r
u1
u2
)
⇒ 0 ≤ (−1)r + d1u1 + d2u2
max c1x1 + c2x2
s . t .
{
a11x1 + a12x2 + x3 = b1
a21x1 + a22x2 + x4 = b2
x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0
min b1y1 + b2y2
s . t .
{
a11y1 + a21y2 ≥ c1
a12y1 + a22y2 ≥ c2
y1 ≥ 0, y2 ≥ 0

18.
C = {(r, u1, u2)|r = c1x1 + c2x2 − tw*
u1 = a11x1 + a12x2 + x3 − tb1
u2 = a21x1 + a22x2 + x4 − tb2
t ≥ 0, x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0}
0 ≤ (−1)r + d1u1 + d2u2 (r, u1, u2) ∈ C
t ≥ 0, x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0
⇒ 0 ≤ (−1)(c1x1 + c2x2 − tw*) + d1(a11x1 + a12x2 + x3 − tb1) + d2(a21x1 + a22x2 + x4 − tb2)
⇒ 0 ≤ t(w* − b1d1 − b2d2)
+x1(−c1 + d1a11 + d2a21)
+x2(−c2 + d2a12 + d2a22)
+x3d1
+x4d2
max c1x1 + c2x2
s . t .
{
a11x1 + a12x2 + x3 = b1
a21x1 + a22x2 + x4 = b2
x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0
min b1y1 + b2y2
s . t .
{
a11y1 + a21y2 ≥ c1
a12y1 + a22y2 ≥ c2
y1 ≥ 0, y2 ≥ 0

19.
C = {(r, u1, u2)|r = c1x1 + c2x2 − tw*
u1 = a11x1 + a12x2 + x3 − tb1
u2 = a21x1 + a22x2 + x4 − tb2
t ≥ 0, x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0}
0 ≤ (−1)r + d1u1 + d2u2 (r, u1, u2) ∈ C
t ≥ 0, x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0
⇒ 0 ≤ (−1)(c1x1 + c2x2 − tw*) + d1(a11x1 + a12x2 + x3 − tb1) + d2(a21x1 + a22x2 + x4 − tb2)
⇒ 0 ≤ t(w* − b1d1 − b2d2)
+x1(−c1 + d1a11 + d2a21)
+x2(−c2 + d2a12 + d2a22)
+x3d1
+x4d2
min b1y1 + b2y2
s . t .
{
a11y1 + a21y2 ≥ c1
a12y1 + a22y2 ≥ c2
y1 ≥ 0, y2 ≥ 0
t ≥ 0, x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0
w* − b1d1 − b2d2 ≥ 0
−c1 + d1a11 + d2a21 ≥ 0
−c2 + d2a12 + d2a22 ≥ 0
d1 ≥ 0 d2 ≥ 0
max c1x1 + c2x2
s . t .
{
a11x1 + a12x2 + x3 = b1
a21x1 + a22x2 + x4 = b2
x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0

20.
C = {(r, u1, u2)|r = c1x1 + c2x2 − tw*
u1 = a11x1 + a12x2 + x3 − tb1
u2 = a21x1 + a22x2 + x4 − tb2
t ≥ 0, x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0}
0 ≤ (−1)r + d1u1 + d2u2 (r, u1, u2) ∈ C
t ≥ 0, x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0
⇒ 0 ≤ (−1)(c1x1 + c2x2 − tw*) + d1(a11x1 + a12x2 + x3 − tb1) + d2(a21x1 + a22x2 + x4 − tb2)
⇒ 0 ≤ t(w* − b1d1 − b2d2)
+x1(−c1 + d1a11 + d2a21)
+x2(−c2 + d2a12 + d2a22)
+x3d1
+x4d2
min b1y1 + b2y2
s . t .
{
a11y1 + a21y2 ≥ c1
a12y1 + a22y2 ≥ c2
y1 ≥ 0, y2 ≥ 0
t ≥ 0, x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0
w* ≥ b1d1 + b2d2
d1a11 + d2a21 ≥ c1
d1a12 + d2a22 ≥ c2
d1 ≥ 0 d2 ≥ 0
max c1x1 + c2x2
s . t .
{
a11x1 + a12x2 + x3 = b1
a21x1 + a22x2 + x4 = b2
x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0

21.
C = {(r, u1, u2)|r = c1x1 + c2x2 − tw*
u1 = a11x1 + a12x2 + x3 − tb1
u2 = a21x1 + a22x2 + x4 − tb2
t ≥ 0, x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0}
0 ≤ (−1)r + d1u1 + d2u2 (r, u1, u2) ∈ C
t ≥ 0, x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0
⇒ 0 ≤ (−1)(c1x1 + c2x2 − tw*) + d1(a11x1 + a12x2 + x3 − tb1) + d2(a21x1 + a22x2 + x4 − tb2)
⇒ 0 ≤ t(w* − b1d1 − b2d2)
+x1(−c1 + d1a11 + d2a21)
+x2(−c2 + d2a12 + d2a22)
+x3d1
+x4d2
t ≥ 0, x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0
w* ≥ b1d1 + b2d2
d1a11 + d2a21 ≥ c1
d1a12 + d2a22 ≥ c2
d1 ≥ 0 d2 ≥ 0
max c1x1 + c2x2
s . t .
{
a11x1 + a12x2 + x3 = b1
a21x1 + a22x2 + x4 = b2
x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0
(d1, d2)
w*
min b1y1 + b2y2
s . t .
{
a11y1 + a21y2 ≥ c1
a12y1 + a22y2 ≥ c2
y1 ≥ 0, y2 ≥ 0

22.
w* ≥ b1d1 + b2d2
d1a11 + d2a21 ≥ c1
d1a12 + d2a22 ≥ c2
d1 ≥ 0 d2 ≥ 0
(d1, d2)
w*
x = (x1, ⋯, xn) y = (y1, ⋯, ym)
f =
n
∑
j=1
cjxj ≤
m
∑
i=1
biyi = g
w* x = (x*1
, x*2
) w* ≤ b1d1 + b2d2 = g
max c1x1 + c2x2
s . t .
{
a11x1 + a12x2 + x3 = b1
a21x1 + a22x2 + x4 = b2
x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0
min b1y1 + b2y2
s . t .
{
a11y1 + a21y2 ≥ c1
a12y1 + a22y2 ≥ c2
y1 ≥ 0, y2 ≥ 0

23.
w* ≥ b1d1 + b2d2
d1a11 + d2a21 ≥ c1
d1a12 + d2a22 ≥ c2
d1 ≥ 0 d2 ≥ 0
(d1, d2)
w*
w* ≤ b1d1 + b2d2
w* = b1d1 + b2d2
(d1, d2) w*
w*
max c1x1 + c2x2
s . t .
{
a11x1 + a12x2 + x3 = b1
a21x1 + a22x2 + x4 = b2
x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0
min b1y1 + b2y2
s . t .
{
a11y1 + a21y2 ≥ c1
a12y1 + a22y2 ≥ c2
y1 ≥ 0, y2 ≥ 0

25. See you next time
5