This document contains solutions to problems related to MOSFET circuits. Section 16.1 calculates threshold voltage shift for an n-channel MOSFET under different gate-source voltages. Section 16.2 determines transistor parameters from output characteristics. Section 16.3 finds the transistor operating point for a different load resistance. Sections 16.4 through 16.9 solve additional problems involving MOSFET biasing, power calculations, and logic gate output voltages.

1. Chapter 16
Problem Solutions
16.1
(a)
2e ∈s N a
ΔVTN = ⎡ 2φ fp + VSB − 2φ fp ⎤
Cax ⎣ ⎦
∈ax (3.9)(8.85 × 10 −14 )
Cax = = = 7.67 × 10−8
tax 450 × 10−8
2e ∈s N a = ⎡ 2 (1.6 × 10 −19 ) (11.7 ) ( 8.85 × 10−14 )( 8 × 1015 ) ⎤
1/ 2
⎣ ⎦ = 5.15 × 10 −8
Then
5.15 × 10−8 ⎡ ⎤
ΔVTN = ⋅ 2(0.343) + VSB − 2(0.343) ⎦
7.67 × 10−8 ⎣
For VSB = 1 V :
ΔVTN = 0.671 ⎡ 1.686 − 0.686 ⎤ ⇒ ΔVTN = 0.316 V
⎣ ⎦
For VSB = 1 V :
⎡ ⎤
ΔVTN = 0.671 ⎣ 2.686 − 0.686 ⎦ ⇒ ΔVTN = 0.544 V
(b) For VGS = 2.5 V, VDS = 5 V, transistor biased in the saturation region.
ID = K n (VGS − VTN ) 2
For VSB = 0,
ID = 0.2(2.5 − 0.8) 2 = 0.578 mA
For VSB = 1,
I D = 0.2 ( 2.5 − [ 0.8 + 0.316]) = 0.383 mA
2
For VSB = 2,
I D = 0.2 ( 2.5 − [ 0.8 + 0.544]) = 0.267 mA
2
16.2
(a)
VDD − vO
ID = = K n ⎡ 2(VGS − VTN )vO − vO ⎤
⎣
2
⎦
RD
5 − (0.1)
= K n ⎡ 2 ( 5 − 0.8 )( 0.1) − ( 0.1) ⎤
2
40 × 10 3 ⎣ ⎦
−5
8 × 10 ⎛ W ⎞
or K n = 1.476 × 10−4 A / V 2 = ⎜ ⎟
2 ⎝L⎠
⎛W ⎞
So that ⎜ ⎟ = 3.69
⎝L⎠
b. From Equation (16.10).
K n RD [VIt − VTN ] + [VIt − VTN ] − VDD = 0
2
(0.1476)(40) [VIt − 0.8] + [VIt − 0.8] − 5 = 0
2
−1 ± (1) 2 + 4(0.1476)(40)(5)
or [VIt − 0.8] =
2(0.1476)(40)
or [VIt − 0.8] = 0.839

2. So that VIt = 1.64 V
P = I D (max) ⋅ VDD
5 − (0.1)
and I D (max) = = 0.1225 mA
40
or P = 0.6125 mW
16.3
a. From Equation (16.10), the transistor point is found from
K n RD (VIt − VTN ) 2 + (VIt − VTN ) − VDD = 0
K n = 50 μ A / V 2 , RD = 20 k Ω, VTN = 0.8 V
(0.05)(20)(VIt − VTN ) 2 + (VIt − VTN ) − 5 = 0
−1 ± 1 + 4(0.05)(20)(5)
VIt − VTN = = 1.79 V So VIt = 2.59 V
2(0.05)(20)
V0t = 1.79 V
Output voltage for vI = 5 V is determined from Equation (16.12):
v0 = 5 − (0.05)(20) ⎡ 2(5 − 0.8)v0 − v0 ⎤
⎣
2
⎦
2
v0 − 9.4v0 + 5 = 0
9.4 ± (9.4) 2 − 4(1)(5)
So v0 = = 0.566 V
2(1)
b. For RD = 200 kΩ,
−1 ± 1 + 4(0.05)(200)(5)
(VIt − VTN ) = = 0.659 V So VIt = 1.46 V
2(0.05)(200)
V0t = 0.659 V
v0 = 5 − (0.05)(200) ⎡ 2 ( 5 − 0.8 ) v0 − v0 ⎤
⎣
2
⎦
2
or 10v0 − 85v0 + 5 = 0
(85 ) − 4 (10 )( 5 )
2
85 ±
v0 = = 0.0592 V
2 (10 )
16.4
(a) P = IV

3. 0.25 = I (33) ⇒ I = 75.76 μA
3.3 − 0.15
R= ⇒ R = 41.6 K
0.07576
⎛ k ′ ⎞⎛ W ⎞
I = ⎜ n ⎟ ⎜ ⎟ (VGS − VTN )
2
⎝ 2 ⎠⎝ L ⎠
⎛ 80 ⎞ ⎛ W ⎞ ⎛W ⎞
75.76 = ⎜ ⎟ ⎜ ⎟ ( 3.3 − 0.8 ) ⇒ ⎜ ⎟ = 0.303
2
⎝ 2 ⎠⎝ L ⎠ ⎝L⎠
(b)
VDS (sat) = VGS − VTN
V − VDS (sat)
I D = K n (VGS − VTN ) = DD
2
R
⎛ 0.08 ⎞ 3.3 − (VGS − 0.8 )
⎟ ( 0.303) (VGS − 1.6VGS + 0.64 ) =
2
⎜
⎝ 2 ⎠ 41.6
0.504 (VGS − 1.6VGS + 0.64 ) = 4.1 − VGS
2
2
0.504VGS + 0.1936VGS − 3.777 = 0
−0.1936 ± 0.03748 + 4(0.504)(3.777)
VGS =
2(0.504)
VGS = 2.55 V
For 0.8 ≤ VGS ≤ 2.55 V
Transistor biased in saturation region
16.5
(a)
P = I ⋅ VDD
0.25 = I (3.3) ⇒ I = 75.76 μA
For Sat Load
⎛ 80 ⎞ ⎛ W ⎞ ⎛W ⎞
I = 75.76 = ⎜ ⎟ ⎜ ⎟ ( 3.3 − 0.15 − 0.8 ) ⇒ ⎜ ⎟ = 0.343
2
⎝ 2 ⎠ ⎝ L ⎠L ⎝ L ⎠L
⎛ 80 ⎞ ⎛ 80 ⎞ ⎛ W ⎞
⎜ ⎟ ( 0.343)( 3.3 − 0.15 − 0.8 ) = I = 75.76 = ⎜ ⎟ ⎜ ⎟ ⎡ 2 ( 2.5 − 0.8 )( 0.15 ) − ( 0.15 ) ⎤
2 2
⎝ 2⎠ ⎝ 2 ⎠ ⎝ L ⎠D ⎣ ⎦
⎛W ⎞
⎜ ⎟ = 3.89
⎝ L ⎠D
Eq 16.21
⎛ 3.89 ⎞
3.3 − 0.8 + 0.8 ⎜1 +
⎜ ⎟
⎝ 0.343 ⎟ 5.994
⎠=
VIt =
3.89 4.3677
1+
0.343
0.8 ≤ VGS ≤ 1.372 V
16.6
(a) From Equation (16.23)
KD ⎡ K
2 3 − 0.5 )( 0.25 ) − ( 0.25 ) ⎤ = ( 3 − 0.25 − 0.5 ) ⇒ D = 4.26
⎣ (
2 2
KL ⎦ KL

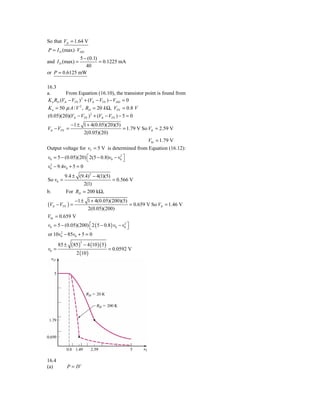
4. KD ⎡ K
2 2.5 − 0.5 )( 0.25 ) − ( 0.25 ) ⎤ = ( 3 − 0.25 − 0.5 ) ⇒ D = 5.4
⎣ (
2 2
(b)
KL ⎦ KL
iD = K L (VGSL − VTNL ) = K L (VDD − vO − VTNL ) 2
2
(c) ⎛ 0.080 ⎞
⎟ (1)(3 − 0.25 − 0.5) ⇒ iD = 0.203 mA
2
=⎜
⎝ 2 ⎠
P = iD ⋅ VDD = (0.203)(3) ⇒ P = 0.608 mW
for both parts (a) and (b).
16.7
P = 0.4 mW = iD ⋅ VDD = iD (3) ⇒ iD = 0.1333 mA
iD = K L (VDD − vO − VTNL ) 2
⎛ 0.080 ⎞ ⎛ W ⎞ ⎛W ⎞
⎟ ⎜ ⎟ ( 3 − 0.1 − 0.5 ) = ( 0.2304 ) ⎜ ⎟
2
0.1333 = ⎜
⎝ 2 ⎠ ⎝ L ⎠L ⎝ L ⎠L
⎛W ⎞
So ⎜ ⎟ = 0.579
⎝ L ⎠L
KD ⎡
2 2.5 − 0.5 )( 0.1) − ( 0.1) ⎤ = ( 3 − 0.1 − 0.5 )
⎣ (
2 2
KL ⎦
KD ⎛W ⎞
⇒ = 14.8 so that ⎜ ⎟ = 8.55
KL ⎝ L ⎠D
VIt =
(
3 − 0.5 + 0.5 1 + 14.8 )
1 + 14.8
or
VIt = 1.02 V , VOt = 0.52 V
16.8
We have
KD
⎣ 2 ( vI − VTND ) vO − vO ⎦ = (VDD − vO − VTNL )
2
⎡ 2
⎤
KL
(W / L )D ⎡
2 V − V − VTN )( 0.08VDD ) − ( 0.08VDD ) ⎤ = (VDD − 0.08VDD − VTN )
⎣ ( DD TN
2 2
(W / L )L ⎦
(W / L )D ⎡
⎣ 2 (VDD − 2 ( 0.2 )VDD ) ( 0.08VDD ) − 0.0064VDD ⎤ = ⎡( 0.92 − 0.2 )VDD ⎤ = 0.5184VDD
2 2 2
(W / L )L ⎦ ⎣ ⎦
(W / L )D (W / L )D
[0.096] = 0.5184 ⇒ = 5.4
(W / L )L (W / L )L
16.9
VOH = VB − VTN = Logic 1
So
(a) VB = 4 V ⇒ VOH = 3V
(b) VB = 5 V ⇒ VOH = 4V
(c) VB = 6 V ⇒ VOH = 5V
(d) VB = 7 V ⇒ VOH = 5 V ,since VDS = 0
For vI = VOH

5. K D ⎡ 2 ( vI − VT ) vO − vO ⎤ = K L [VB − vO − VT ]
2 2
⎣ ⎦
Then
(1) ⎡ 2 ( 3 − 1)VOL − VOL ⎤ = ( 0.4 ) [ 4 − VOL − 1]
2
(a) ⎣
2
⎦ ⇒ VOL = 0.657 V
(1) ⎣ 2 ( 4 − 1)VOL − V ⎦ = ( 0.4 ) [5 − VOL − 1] ⇒ VOL = 0.791 V
2
(b) ⎡ 2
OL
⎤
(1) ⎡ 2 ( 5 − 1)VOL − VOL ⎤ = ( 0.4 ) [6 − VOL − 1]
2
(c) ⎣
2
⎦ ⇒ VOL = 0.935 V
(d) Load in non-sat region
iDD = iOL
(1) ⎡ 2 ( 5 − 1) VOL − VOL ⎤ = ( 0.4 ) ⎡ 2 ( 7 − VOL − 1)( 5 − VOL ) − ( 5 − VOL ) ⎤
2 2
⎣ ⎦ ⎣ ⎦
8VOL − VOL = ( 0.4 ) ⎡ 2 ( 6 − VOL )( 5 − VOL ) − ( 25 − 10VOL + VOL ) ⎤
2
⎣
2
⎦
= ( 0.4 ) ⎡ 2 ( 30 − 11VOL + VOL ) − 25 + 10VOL − VOL ⎤
⎣
2 2
⎦
= ( 0.4 ) ⎡60 − 22VOL + 2VOL − 25 + 10VOL − VOL ⎤
⎣
2 2
⎦
2 2
8VOL − VOL = 14 − 4.8VOL + 0.4VOL
2
1.4VOL − 12.8VOL + 14 = 0
12.8 ± 163.84 − 4 (1.4 )(14 )
VOL =
2 (1.4 )
VOL = 1.27V
For load
VDS ( sat ) = 7 − 1.27 − 1 = 4.73V
VDS = 5 − 1.27 = 3.73 non-sat
16.10
a. For load VOt = VDD + VTNL = 5 − 2 = 3 V
KD
⋅ (VIt − VTND ) = −VTNL
KL
500
(VIt − 0.8 ) = − ( −2 )
100
⇒ VIt = 1.69 V ⎫
⎬ Load
VOt = 3 V ⎭
Driver: VOt = VIt − VTND = 1.69 − 0.8 = 0.89 V
VIt = 1.69 V ⎫
⎬ Driver
V0t = 0.89 V ⎭
b. From Equation (16.29(b)):
500 2
⋅ ⎣ 2(5 − 0.8)v0 − v0 ⎦ = ⎡ − ( −2 ) ⎤
⎡ 2
⎤ ⎣ ⎦
100
2
5v0 − 42v0 + 4 = 0
( 42 ) − 4 ( 5)( 4 )
2
42 ±
v0 = ⇒ v0 = 0.0963 V
2 (5)
2
iD = K L ( −VTNL ) = 100 ⎣ − ( −2 ) ⎦ ⇒ iD = 400 μ A
2
c. ⎡ ⎤

6. 16.11
⎛ 500 ⎞ ⎡
⎟ ⎣ 2 ( 3 − 0.5 )( 0.1) − ( 0.1) ⎤ = ( −VTNL )
2 2
⎜ ⎦
⎝ 50 ⎠
So
( −VTNL )
2
= 4.9 ⇒ VTNL = −2.21 V
16.12
(a)
P = iD ⋅ VDD
150 = iD ⋅ ( 3) ⇒ iD = 50 μ A
iD = K L (−VTNL ) 2
⎛ 80 ⎞ ⎛ W ⎞ 2 ⎛W ⎞
50 = ⎜ ⎟ ⎜ ⎟ ⎡ − ( −1) ⎤ ⇒ ⎜ ⎟ = 1.25
⎝ 2 ⎠ ⎝ L ⎠L ⎣ ⎦
⎝ L ⎠L
KD ⎡
2 ( 3 − 0.5 )( 0.1) − ( 0.1) ⎤ = ⎡ − ( −1) ⎤
2 2
KL ⎣ ⎦ ⎣ ⎦
K D (W / L ) D ⎛W ⎞
= = 2.04 ⇒ ⎜ ⎟ = 2.55
K L (W / L ) L ⎝ L ⎠D
For the Load:
VOt = VDD + VTNL = 3 − 1 ⇒ VOt = 2 V
2.04 (VIt − 0.5 ) = ⎡ − ( −1) ⎤ ⇒ VIt = 1.20 V
⎣ ⎦
For the Driver:
VOt = VIt − VTND = 1.20 − 0.5 ⇒ VOt = 0.70 V
VIt = 1.20 V
(b) NM L = VIL − VOLU
NM H = VOHU − VIH
⎡ − ( −1) ⎤
⎣ ⎦
VIL = 0.5 + = 0.902 V
( 2.04 )(1 + 2.04 )
2 ⎡ − ( −1) ⎤
VIH = 0.5 + ⎣ ⎦ = 1.31 V
3 ( 2.04 )
Then VOHU = ( 3 − 1) + ( 2.04 )( 0.902 − 0.5 ) = 2.82 V
(1.31 − 0.5)
VOLU = = 0.405 V
2
NM L = 0.902 − 0.405 ⇒ NM L = 0.497 V
NM H = 2.82 − 1.31 ⇒ NM H = 1.51 V
16.13
a. From Equation (16.29(b)):
⎛W ⎞ ⎡ ⎛W ⎞
⎜ ⎟ ⎣ 2 ( 2.5 − 0.5 )( 0.05 ) − ( 0.05 ) ⎤ = ⎜ ⎟ [− ( −1)]
2 2
⎝ L ⎠D ⎦ ⎝ L ⎠L
⎛W ⎞
⎜ ⎟ =1
⎝ L ⎠L

7. ⎛W ⎞
Then ⎜ ⎟ = 5.06
⎝ L ⎠D
⎛ 80 ⎞ 2
b. iD = ⎜ ⎟ (1) ⎡ − ( −1) ⎤
⎣ ⎦
⎝ 2⎠
or iD = 40 μ A
P = iD ⋅ VDD = ( 40 )( 2.5 ) ⇒ P = 100 μ W
16.14
a. i. vI = 0.5 V ⇒ iD = 0 ⇒ P = 0
ii. vI = 5 V, From Equation (16.12),
v0 = 5 − ( 0.1)( 20 ) ⎡ 2 ( 5 − 1.5 ) v0 − v0 ⎤
⎣
2
⎦
2
2v0 − 15v0 + 5 = 0
(15 ) − 4 ( 2 )( 5 )
2
15 ±
v0 = ⇒ v0 = 0.35 V
2 ( 2)
5 − 0.35
iD = = 0.2325 mA
20
P = iD ⋅ VDD = ( 0.2325 )( 5 ) ⇒ P = 1.16 mW
b. i. vI = 0.25 V ⇒ iD = 0 ⇒ P = 0
ii. vI = 4.3 V, From Equation (16.23),
100 ⎣ 2 ( 4.3 − 0.7 ) v0 − v0 ⎦ = 10 [5 − v0 − 0.7 ]
2
⎡ 2
⎤
10 ⎡7.2v0 − v0 ⎤ = 18.49 − 8.6v0 + v0
⎣
2
⎦
2
Then
2
11v0 − 80.6v0 + 18.49 = 0
(80.6 ) − 4 (11)(18.49 )
2
80.6 ±
v0 = ⇒ v0 = 0.237 V
2 (11)
Then
iD = 10 [5 − 0.237 − 0.7 ] = 165 μ A
2
P = iD ⋅ VDD = (165 )( 5 ) ⇒ P = 825 μ W
c. i. vI = 0.03 V ⇒ iD = 0 ⇒ P = 0
ii. vI = 5 V
2
iD = K L ( −VTNL ) = (10 ) ⎡ − ( −2 ) ⎤ = 40 μ A
2
⎣ ⎦
P = iD ⋅ VDD = ( 40 )( 5 ) ⇒ P = 200 μ W
16.15
vo1 = 3.8V
Load & Driver in Sat, region, ML1, MD1

8. iDL = iDD
⎛W ⎞ ⎛W ⎞
⎜ ⎟ ( vGSL − VTNL ) = ⎜ ⎟ ( vGSD − VTND )
2 2
⎝ L ⎠L ⎝ L ⎠D
(1) ( 5 − vo1 − 0.8 ) = (10 )( vI − 0.8 )
2 2
0.16 = 10 ( vI − 0.8 )
2
vI = 0.9265V
Now MD2: Non Sat and ML2: Sat
iDL = iDD
⎛W ⎞ ⎛W ⎞
⎜ ⎟ ( vGSL − VTNL ) = ⎜ ⎟ ⎡ 2 ( vo1 − VTND ) vo 2 − vo 2 ⎤
2 2
⎣ ⎦
⎝ L ⎠L ⎝ L ⎠D
(1)( 5 − vo 2 − 0.8 ) = (10 ) ⎡ 2 ( 3.8 − 0.8 ) vo 2 − vo 2 ⎤
2 2
⎣ ⎦
( 4.2 − vo 2 )
2
= 10 ⎡ 6vo 2 − vo 2 ⎤
⎣
2
⎦
2 2
17.64 − 8.4vo 2 + vo 2 = 60vo 2 − 10vo 2
2
11vo 2 − 68.4vo 2 + 17.64 = 0
68.4 ± 4678.56 − 4 (11)(17.64 )
vo 2 =
2 (11)
vo 2 = 0.270 V
16.16
a. From Equation (16.41),
2 ⎡ − ( −2 ) ⎤
VIH = 0.8 + ⎣ ⎦ ⇒ V = 1.95 V = v
01
3( 4)
IH
M D 2 in non-saturation and M L 2 in saturation.
K D ⎡ 2 ( v01 − VTND ) v02 − v02 ⎤ = K L ( −VTNL )
2 2
⎣ ⎦
2
4 ⎣ 2 (1.95 − 0.8 ) v02 − v02 ⎦ = (1) ⎡ − ( −2 ) ⎤
⎡ 2
⎤ ⎣ ⎦
2
4v02 − 9.2v02 + 4 = 0
( 9.2 ) − 4 ( 4 )( 4 )
2
9.2 ±
v02 = ⇒ v02 = 0.582 V
2 ( 4)
Both M D1 and M L1 in saturation region. From Equation (16.28(b)).
4 ⋅ ( vI − 0.8 ) = − ( −2 )
or vI = 1.8 V
( +2 )
b. VIL = 0.8 + = 1.25 V = v01
4 (1 + 4 )
M D 2 in saturation, M L 2 in non-saturation

9. K D [ vO1 − VTND ] = K L ⎡ 2 ( −VTNL )( 5 − vO 2 ) − ( 5 − vO 2 ) ⎤
2 2
⎣ ⎦
4 (1.25 − 0.8 ) = 2 ( 2 )( 5 − v02 ) − ( 5 − v02 )
2 2
( 5 − v02 ) − 4 ( 5 − v02 ) + 0.81 = 0
2
( 4) − 4 (1)( 0.81)
2
4±
5 − v02 = = 0.214 V
2 (1)
so
v02 = 4.786 V
To find vI :
4 ( v01 − 0.8 ) = (1) ( − ( −2 ) )
2 2
v01 − 0.8 = 1
v01 − 1.8 = V
c. VIH = 1.95 V, VIL = 1.25 V
16.17
a. i. Neglecting the body effect,
v0 = VDD − VTN
Assume VDD = 5 V, then v0 = 4.2 V
ii. Taking the body effect into account: From Problem 16.1.
VTN = VTN 0 + 0.671 ⎡ 0.686 + VSB − 0.686 ⎤
⎣ ⎦
and VSB = v0
Then
(
v0 = 5 − ⎡ 0.8 + 0.671 0.686 + v0 − 0.686 ⎤
⎣ ⎦ )
v0 = 4.756 − 0.671 0.686 + v0
0.671 0.686 + v0 = 4.756 − v0
0.450 ( 0.686 + v0 ) = 22.62 − 9.51v0 + v0
2
2
v0 − 9.96v0 + 22.3 = 0
( 9.96 ) − 4 ( 22.3)
2
9.96 ±
v0 = ⇒ v0 = 3.40 V
2
b. PSpice results similar to Figure 16.13(a).
16.18
Results similar to Figure 16.13(b).
16.19
a. M X on, M Y cutoff.
From Equation (16.29(b)):
KD ⎡
2 5 − 0.8 )( 0.2 ) − ( 0.2 ) ⎤ = ⎡ − ( −2 ) ⎤
2
⎣ (
2
KL ⎦ ⎣ ⎦
KD
or = 2.44
KL
b. For v X = vY = .5 V

10. 2
2 ( 2.44 ) ⎣ 2 ( 5 − 0.8 ) v0 − v0 ⎤ = ⎡ − ( −2 ) ⎤
⎡ 2
⎦ ⎣ ⎦
2
4.88v0 − 41.0v0 + 4 = 0
( 41) − 4 ( 4.88 )( 4 )
2
41 ±
v0 =
2 ( 4.88 )
or
v0 = 0.0987 V
c.
⎛ 80 ⎞ 2
iD = ⎜ ⎟ (1) ⎡ − ( −2 ) ⎤ = 160 μ A
⎝ 2⎠ ⎣ ⎦
P = (160 )( 5 ) ⇒ P = 800 μ W
for both parts (a) and (b).
16.20
(a) Maximum value of vO in low state- when only one input is high, then,
KD ⎡
2 ( 3 − 0.5 )( 0.1) − ( 0.1) ⎤ = ⎡ − ( −1) ⎤
2 2
KL ⎣ ⎦ ⎣ ⎦
KD
= 2.04
KL
(b)
P = iD ⋅ VDD
0.1 = iD (3) ⇒ iD = 33.3 μ A
⎛ k′ ⎞⎛ W ⎞
iD = ⎜ n ⎟ ⎜ ⎟ ( −VTNL )
2
⎝ 2 ⎠ ⎝ L ⎠L
⎛ 80 ⎞⎛ W ⎞ 2 ⎛W ⎞
33.3 = ⎜ ⎟⎜ ⎟ ⎡ − ( −1) ⎤ ⇒ ⎜ ⎟ = 0.8325
⎣ ⎦
⎝ 2 ⎠⎝ L ⎠ L ⎝ L ⎠L
⎛W ⎞
Then ⎜ ⎟ = 1.70
⎝ L ⎠D
2
(c) 3 ( 2.04 ) ⎡ 2 ( 3 − 0.5 ) vO − vO ⎤ = ⎡ − ( −1) ⎤ ⇒ vO = 0.0329 V
⎣
2
⎦ ⎣ ⎦
16.21
(a) One driver in non-sat,
I D = K L ( −VTNL ) = K D ⎡ 2 (VGS − VTND ) VDSD − VDSD ⎤
2 2
⎣ ⎦
K
⎡ − ( −1) ⎤ = D ⎡ 2 ( 3.3 − 0.5 )( 0.1) − ( 0.1) ⎤
2 2
⎣ ⎦ KL ⎣ ⎦
KD
= 1.82
KL
(b)

11. P = ± VDD
0.1 = ± ( 3.3) ⇒ I = 30.3 μ A
⎛ 80 ⎞ ⎛ W ⎞ 2 ⎛W ⎞
30.3 = I = ⎜ ⎟ ⎜ ⎟ ⎡ − ( −1) ⎤ ⇒ ⎜ ⎟ = 0.7575
⎣ ⎦
⎝ 2 ⎠ ⎝ L ⎠L ⎝ L ⎠L
⎛W ⎞
⎜ ⎟ = 1.38
⎝ L ⎠D
(c)
0.1
(i) Two inputs High, vo ≈ = 0.05 V
2
0.1
(ii) Three inputs High, vo ≈ = 0.0333 V
3
0.1
(iii) Four inputs High, vo ≈ = 0.025 V
4
16.22
a.
P = iD ⋅ VDD
250 = iD ( 5 ) ⇒ iD = 50 μΑ
⎛ k' ⎞⎛W ⎞
iD = ⎜ n ⎟ ⎜ ⎟ [ −VTNL1 ]
2
⎝ 2 ⎠ ⎝ L ⎠ ML1
⎛ 60 ⎞ ⎛ W ⎞ 2
50 = ⎜ ⎟ ⎜ ⎟ ⎡ − ( −2 ) ⎤
⎣ ⎦
⎝ 2 ⎠ ⎝ L ⎠ ML1
⎛W ⎞
So that ⎜ ⎟ = 0.417
⎝ L ⎠ ML1
KD
⎡ 2 ( vI − VTND ) vO − vO ⎤ = [ −VTNL ]
2 2
KL ⎣ ⎦
KD ⎡
2 5 − 0.8 )( 0.15 ) − ( 0.15 ) ⎤ = ⎡ − ( −2 ) ⎤
2
⎣ (
2
KL ⎦ ⎣ ⎦
KD ⎛W ⎞
or = 3.23 ⇒ ⎜ ⎟ = 1.35
KL ⎝ L ⎠ MD1
b. For v X = vY = 0 ⇒ v01 = 5 and v03 = 4.2
Then
K D 2 ⎡ 2 ( vO1 − VTND ) vO 2 − vO 2 ⎤ + K D 3 ⎡ 2 ( vO 3 − VTND ) vO 2 − vO 2 ⎤ = K L 2 [ −VTNL 2 ]
2 2 2
⎣ ⎦ ⎣ ⎦
K D 2 ∝ 8, K D 3 ∝ 8, K L 2 ∝ 1
2
8 ⎡ 2 ( 5 − 0.8 ) v02 − v02 ⎤ + 8 ⎡ 2 ( 4.2 − 0.8 ) v02 − v02 ⎤ = (1) ⎡ − ( −2 ) ⎤
⎣
2
⎦ ⎣
2
⎦ ⎣ ⎦
2 2
67.2v02 − 8v02 + 54.4v02 − 8v02 = 4
Then
2
16v0 − 121.6v0 + 4 = 0
(121.6 ) − 4 (16 )( 4 )
2
121.6 ±
v02 =
2 (16 )
So v02 = 0.0330 V
16.23

12. a. We can write
K x ⎡ 2 ( v X − VTN ) vDSX − vDSX ⎤ = K y ⎡ 2 ( vY − vDSX − VTN ) vDSY − vDSY ⎤ = K L [VDD − vO − VTN ]
2 2 2
⎣ ⎦ ⎣ ⎦
where v0 = vDSX + vDSY
We have
v X = vY = 9.2 V , VDD = 10 V , VTN = 0.8 V
2 2
As a good first approximation, neglect the vDSX and vDSY terms. Let v0 ≈ 2vDSX . Then from the first and
third terms in the above equation.
9 ⎡ 2 ( 9.2 − 0.8 ) vDSX ⎤ ≅ (1)(10 − 2vDSX − 0.8 )
2
⎣ ⎦
(151.2 ) vDSX ≅ 84.64 − 36.8vDSX
So that vDSX = 0.450 V
From the first and second terms of the above equation.
9 ⎡ 2 ( 9.2 − 0.8 ) vDSX ⎤ ≅ 9 ⎡ 2 ( 9.2 − vDSX − 0.8 ) vDSY ⎤
⎣ ⎦ ⎣ ⎦
or
(16.8)( 0.45) = 2 ( 9.2 − 0.45 − 0.8) vDSY
which yields vDSY = 0.475 V
Then v0 = vDSX + vDSY = 0.450 + 0.475
or v0 = 0.925 V
We have vGSX = 9.2 V
and vGSY = 9.2 − vDSX = 9.2 − 0.45
or vGSY = 8.75 V
b. Since v0 is close to ground potential, the body effect will have minimal effect on the results. From
a PSpice analysis:
For part (a):
vDSX = 0.462 V, vDSY = 0.491 V, v0 = 0.9536 V, vGSX = 9.2 V, and vGSY = 8.738 V
For part (b):
vDSX = 0.441 V, vDSY = 0.475 V, v0 = 0.9154 V, vGSX = 9.2 V, and vGSY = 8.759 V
16.24
a. We can write
K x ⎡ 2 ( v X − VTNX ) vDSX − vDSX ⎤ = K y ⎡ 2 ( vY − vDSX − VTNY ) vDSY − vDSY ⎤ = K L [ −VTNL ]
2 2 2
⎣ ⎦ ⎣ ⎦
2
From the first and third terms, (neglect vDSX ),
2
4 ⎡ 2 ( 5 − 0.8 ) vDSX ⎤ = (1) ⎡ − ( −1.5 ) ⎤
⎣ ⎦ ⎣ ⎦
or vDSX = 0.067 V
2
From the second and third terms, (neglect vDSY ),
2
4 ⎡ 2 ( 5 − 0.067 − 0.8 ) vDSY ⎤ = (1) ⎡ − ( −1.5 ) ⎤
⎣ ⎦ ⎣ ⎦
or vDSY = 0.068 V
Now
vGSX = 5, vGSY = 5 − 0.067 ⇒ vGSY = 4.933 V
and v0 = vDSX + vDSY ⇒ v0 = 0.135 V
Since v0 is close to ground potential, the body-effect has little effect on the results.
16.25

13. 0.2
(a) We have VDS of each driver ≈ = 0.05 V
4
K L [ −VTNL ] = K D ⎡ 2 (VGSD − VTN ) VDSD
2
⎣ − VDSD ⎤
2
⎦
K
⎡ − ( −1) ⎤ = D ⎡ 2 ( 3.3 − 0.4 )( 0.05 ) − ( 0.05 ) ⎤
2 2
⎣ ⎦ KL ⎣ ⎦
KD
= 3.478
KL
(b)
P = I VDD
0.15 = I ( 3.3) ⇒ I = 45.45 μ A
⎛ 80 ⎞ ⎛ W ⎞ 2 ⎛W ⎞
45.45 = ⎜ ⎟ ⎜ ⎟ ⎡ − ( −1) ⎤ ⇒ ⎜ ⎟ = 1.14
⎣ ⎦
⎝ 2 ⎠ ⎝ L ⎠L ⎝ L ⎠L
⎛W ⎞
⎜ ⎟ = 3.95
⎝ L ⎠D
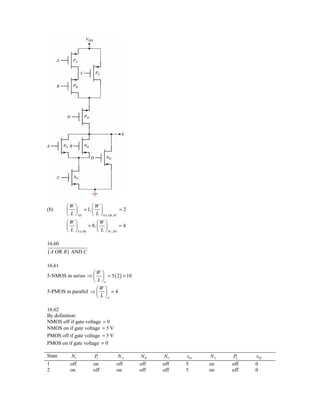
16.26
Complement of (B AND C) OR A ⇒ ( B ⋅ C ) + A
16.27
Considering a truth table, we find
A B Y
0 0 0
0 1 1
1 0 1
1 1 0
which shows that the circuit performs the exclusive-OR function.
16.28
( A + B )(C + D)
16.29
(a) Carry-out = A • ( B + C ) + B • C

14. (b) For vO1 = Low = 0.2 V
KD ⎡
2 ( 5 − 0.8 )( 0.2 ) − ( 0.2 ) ⎤ = ⎡ − ( −1.5 ) ⎤ ⇒
2 2
KL ⎣ ⎦ ⎣ ⎦
⎛W ⎞ ⎛W ⎞
For ⎜ ⎟ = 1, then ⎜ ⎟ = 1.37
⎝ L ⎠L ⎝ L ⎠D
⎛W ⎞
So, for M 6 : ⎜ ⎟ = 1.37
⎝ L ⎠6
To achieve the required composite conduction parameter,
⎛W ⎞
For M 1 − M 5 : ⎜ ⎟ = 2.74
⎝ L ⎠1− 5
16.30
AE: VDS ≈ 0.075
⎛W ⎞
(1) ⎡ − ( −1) ⎤ ≅ ⎜ ⎟ ⎡ 2 ( 3.3 − 0.4 )( 0.075 ) − ( 0.075 ) ⎤
2 2
⎣ ⎦ L ⎠D ⎣ ⎦
⎝
⎛W ⎞ ⎛W ⎞ ⎛W ⎞ ⎛W ⎞ ⎛W ⎞
⎜ ⎟ = ⎜ ⎟ = 2.33 ⇒ ⎜ ⎟ = ⎜ ⎟ = ⎜ ⎟ = 4.66
⎝ L ⎠ A ⎝ L ⎠E ⎝ L ⎠ B ⎝ L ⎠C ⎝ L ⎠ D
16.31
Not given

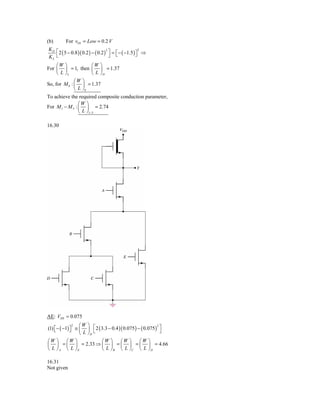
15. 16.32
a. From Equation (16.43),
5 − 0.8 + 0.8
vI = VIt = = VIt = 2.5 V
1+1
p − channel, V0 Pt = 2.5 − ( −0.8 ) ⇒ V0 Pt = 3.3 V
n − channel, V0 Nt = 2.5 − 0.8 ⇒ V0 Nt = 1.7 V
c For vI = 2 V, NMOS in saturation and PMOS in nonsaturation. From Equation (16.49),
( 2 − 0.8)= ⎡ 2 ( 5 − 2 − 0.8 )( 5 − v0 ) − ( 5 − v0 ) ⎤
2 2
⎣ ⎦
1.44 = 4.4(5 − v0 ) − (5 − v0 ) 2
So ( 5 − v0 ) − 4.4 ( 5 − v0 ) + 1.44 = 0
2
( 4.4 ) − 4 (1)(1.44 )
2
4.4 ±
( 5 − v0 ) =
2
or
5 − v0 = 0.356 ⇒ v0 = 4.64 V
By symmetry, for vI = 3 V, v0 = 0.356 V
16.33
⎛ 80 ⎞
(a) K n = ⎜ ⎟ ( 2 ) = 80 μ A / V 2
⎝ 2⎠
⎛ 40 ⎞
K p = ⎜ ⎟ ( 4 ) = 80 μ A / V 2
⎝ 2 ⎠
Kn
VDD + VTP + ⋅ VTN
Kp 3.3 − 0.4 + (1)(0.4)
(i) VIt = =
Kn 1+1
1+
Kp
VIt = 1.65 V
PMOS:
VOt = VIt − VTP = 1.65 − ( −0.4 ) ⇒ VOt = 2.05 V
NMOS:
VOt = VIt − VTN = 1.65 − ( 0.4 ) ⇒ VOt = 1.25 V
(iii) For vO = 0.4 V : NMOS: Non-sat: PMOS:Sat
K n ⎡ 2 (VGSN − VTN )VDS − VDS ⎤ = K p [VSGP + VTP ]
2 2
⎣ ⎦
2 ( vI − 0.4 )( 0.4 ) − ( 0.4 ) = ( 3.3 − vI − 0.4 ) ⇒ vI = 1.89 V
2 2
For vO = 2.9 V , By symmetry
vI = 1.65 − (1.89 − 1.65 ) ⇒ vI = 1.41 V
⎛ 80 ⎞
(b) K n = ⎜ ⎟ ( 2 ) = 80 μ A/V 2
⎝ 2⎠
⎛ 40 ⎞
K p = ⎜ ⎟ ( 2 ) = 40 μ A/V 2
⎝ 2 ⎠

16. 80
3.3 − 0.4 + ⋅ ( 0.4 )
(i) VIt = 40 ⇒ VIt = 1.44 V
80
1+
40
PMOS:
VOt = 1.44 − ( −0.4 ) ⇒ VOt = 1.84 V
NMOS:
VOt = 1.44 − 0.4 ⇒ VOt = 1.04 V
(iii) For vO = 0.4 V
⎦ ( )[
⎡ ⎤ = 40 3.3 − vI − 0.4]2 ⇒ vI = 1.62 V
(80 ) ⎣ 2 ( vI − 0.4 )( 0.4 ) − ( 0.4 )
2
For vO = 2.9 V : NMOS: Sat, PMOS: Non-sat
(80 ) [vI − 0.4] = ( 40 ) ⎡ 2 ( 3.3 − vI − 0.4 )( 0.4 ) − ( 0.4 ) ⎤ ⇒ vI = 1.18 V
2 2
⎣ ⎦
16.34
(a) From Eq. (16.43), switching voltage
(i)
VDD + VTP +
Kn
⋅ VTN 2 ( 4)
Kp 3.3 + ( −0.4 ) + ( 0.4 ) 3.2266
vI t = = 12 = ⇒ vIt = 1.776 V
Kn 2 ( 4) 1.8165
1+ 1+
Kp 12
(ii) v0 = 3.1 V , PMOS, non-sat; NMOS, sat
′
⎛ kp ⎞⎛ W ⎞ ′
⎛ kn ⎞ ⎛ W ⎞
⎜ ⎟ ⎜ ⎟ ⎣ 2 (VSG + VTP ) VSD − VSD ⎦ = ⎜ ⎟ ⎜ ⎟ (VGS − VTN )
2
⎡ 2
⎤
⎝ 2 ⎠⎝ L ⎠p ⎝ 2 ⎠ ⎝ L ⎠n
⎛ 40 ⎞ ⎛ 80 ⎞
⎜ ⎟ (12 ) ⎡ 2 ( 3.3 − vI − 0.4 )( 3.3 − 3.1) − ( 3.3 − 3.1) ⎤ = ⎜ ⎟ ( 4 ) [ vI − 0.4]
2 2
⎝ 2 ⎠ ⎣ ⎦ ⎝ 2⎠
12 [1.16 − 0.4vI − 0.04] = 8 ⎣ vI2 − 0.8vI + 0.16 ⎤
⎡ ⎦
8vI2 − 1.6vI − 12.16 = 0
1.6 ± 2.56 + 4 ( 8 ) (12.16 )
vI = ⇒ vI = 1.337 V
2 (8)
(iii) v0 = 0.2 V PMOS: sat, NMOS, non-sat.
⎛ 40 ⎞ ⎛ 80 ⎞
⎜ ⎟ (12 ) [3.3 − vI − 0.4] = ⎜ ⎟ ( 4 ) ⎡ 2 ( vI − 0.4 )( 0.2 ) − ( 0.2 ) ⎤
2 2
⎝ 2 ⎠ ⎝ 2⎠ ⎣ ⎦
12 ⎡8.41 − 5.8vI + vI2 ⎤ = 8 [ 0.4vI − 0.2]
⎣ ⎦
12vI2 − 72.8vI + 102.52 = 0
72.8 ± 5299.84 − 4 (12 )(102.52 )
vI =
2 (12 )
vI = 2.222 V
(b)

17. 2 ( 6)
3.3 + ( −0.4 ) + ( 0.4 ) 3.5928
(i) vIt = 4 =
2 (6) 2.732
1+
4
vIt = 1.315 V
(ii) From (a), (ii)
4 [1.16 − 0.4vI − 0.04] = 12 ⎡vI2 − 0.8vI + 0.16 ⎤
⎣ ⎦
12vI2 − 8vI − 2.56 = 0
8 ± 64 + 4 (12 )( 2.56 )
vI = ⇒ vI = 0.903 V
2 (12 )
(iii) From (a), (iii)
4⎣⎡8.41 − 5.8vI + vI2 ⎤ = 12 [ 0.4vI − 0.2]
⎦
4vI2 − 28vI + 36.04 = 0
28 ± 784 − 4 ( 4 )( 36.04 )
vI = ⇒ vI = 1.70 V
2 ( 4)
16.35
a. For vO1 = 0.6 < VTN ⇒ vO 2 = 5 V
N1 in nonsaturation and P in saturation. From Equation (16.45),
1
⎡ 2 ( vI − 0.8 )( 0.6 ) − ( 0.6 )2 ⎤ = [5 − vI − 0.8]2
⎣ ⎦
1.2vI − 1.32 = 17.64 − 8.4vI + vI2
or
vI2 − 9.6vI + 18.96 = 0
( 9.6 ) − 4 (1)(18.96 )
2
9.6 ±
vI =
2
or
vI = 2.78 V
b. V0 Nt ≤ v02 ≤ V0 Pt
From symmetry, VIt = 2.5 V
V0 Pt = 2.5 + 0.8 = 3.3 V
and V0 Nt = 2.5 − 0.8 = 1.7 V
So 1.7 ≤ v02 ≤ 3.3 V
16.36
a. V0 Nt ≤ v01 ≤ V0 Pt
By symmetry, VIt = 2.5 V
V0 Pt = 2.5 + 0.8 = 3.3 V
and V0 Nt = 2.5 − 0.8 = 1.7 V
So 1.7 ≤ v01 ≤ 3.3 V
b. For vO 2 = 0.6 < VTN ⇒ vO 3 = 5 V
N 2 in nonsaturation and P2 in saturation. From Equation (16.57),

18. ⎡ 2 ( vI 2 − 0.8 )( 0.6 ) − ( 0.6 )2 ⎤ = [5 − vI 2 − 0.8]2
⎣ ⎦
1.2vI 2 − 1.32 = 17.64 − 8.4vI 2 + vI22
or
vI22 − 9.6vI 2 + 18.96 = 0
So vI 2 = v01 = 2.78 V
For v01 = 2.78, both N1 and P in saturation. Then
1
vI = 2.5 V
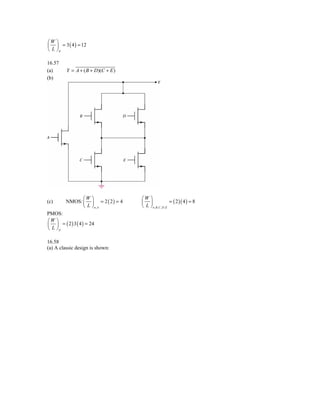
16.37
a.
iPeak = K n ( vI − VTN )
iPeak = 0.1 ⋅ ( 2.5 − 0.8 ) = 0.538 ( mA )
1/ 2
iPeak = 0.1 ⋅ (1.65 − 0.8 ) = 0.269 ( mA )
1/ 2
b.
16.38
⎛ 50 ⎞
(a) K n = ⎜ ⎟ ( 2 ) = 50 μ A / V 2
⎝ 2⎠
⎛ 25 ⎞
K p = ⎜ ⎟ ( 4 ) = 50 μ A / V 2
⎝ 2 ⎠
I D , peak = K n ( v1 − VTN ) = 50 ( 2.5 − 0.8 )
2 2
or I D , peak = 144.5 μ A
(b) K n = 50 μ A / V 2 , K p = 25 μ A/V 2
From Equation (16.55),
50
5 − 0.8 + (0.8)
vIt = 25 = 2.21 V
50
1+
25
Then
I D , peak = K n (VIt − VTN ) 2 = 50 ( 2.21 − 0.8 )
2
or I D , peak = 99.4 μ A
16.39

19. (a) Switching Voltage, Eq. (16.43)
2 ( 4)
3.3 − 0.4 + ( 0.4 )
vIt = 8 = 1.65 V = vIt
2 ( 4)
1+
8
⎛ 80 ⎞
iD, peak = ⎜ ⎟ ( 4 )(1.65 − 0.4 ) ⇒ iD , peak = 250 μA
2
⎝ 2⎠
(b)
2 ( 4)
3.3 − 0.4 + ( 0.4 )
vIt = 4 = 1.436 V = vIt
2 ( 4)
1+
4
⎛ 80 ⎞
iD , peak = ⎜ ⎟ ( 4 )(1.436 − 0.4 ) ⇒ iD , peak = 172 μA
2
⎝ 2⎠
(c)
2 ( 4)
3.3 − 0.4 + ( 0.4 )
vIt = 12 ⇒ vIt = 1.776 V
2 ( 4)
1+
12
⎛ 80 ⎞
iD , peak = ⎜ ⎟ ( 4 )(1.776 − 0.4 ) ⇒ iD , peak = 303 μA
2
⎝ 2⎠
16.40
2
a. P = fCLVDD
For VDD = 5 V, P = (10 × 106 )(0.2 ×10−12 )(5) 2
or P = 50 μ W
For VDD = 15 V, P = (10 × 106 )(0.2 × 10−12 )(15) 2
or P = 450 μ W
b. For VDD = 5 V, P = (10 × 106 )(0.2 ×10−12 )(5) 2
or P = 50 μ W
16.41
(a)
P = fCLVDD = (150 × 106 )( 0.4 ×10−12 ) ( 5 ) = 1.5 × 10 −3 W / inverter
2 2
Total power: PT = ( 2 × 106 )(1.5 × 10−3 ) ⇒ PT = 3000 W !!!!
(b) For f = 300 MHz
1.5 ×10 = ( 300 ×106 )( 0.4 × 10−12 ) VDD ⇒ VDD = 3.54 V
−3 2
16.42
3
(a) P= 7
= 3 × 10−7 W
10
P
(b) P = fCLVDD ⇒ CL =
2
2
fVDD

20. 3 × 10−7
(i) CL = ⇒ CL = 0.0024 pF
( 5 ×10 ) ( 5)
6 2
3 × 10−7
(ii) CL = ⇒ CL = 0.00551pF
( 5 ×10 ) ( 3.3)
6 2
3 × 10−7
(iii) CL = ⇒ CL = 0.0267 pF
( 5 ×10 ) (1.5)
6 2
16.43
10
(a) P= = 2 × 10−6 W
5 × 106
P
(b) CL = 2
fVDD
2 × 10−6
(i) CL = ⇒ CL = 0.01 pF
(8 ×10 ) ( 5)
6 2
2 × 10−6
(ii) CL = ⇒ CL = 0.023 pF
(8 ×10 ) ( 3.3)
6 2
2 × 10−6
(iii) CL = ⇒ CL = 0.111 pF
(8 ×10 ) (1.5)
6 2
16.44
(a) For vI ≅ VDD , NMOS in nonsaturation
iD = K n ⎡ 2 ( vI − VTN ) vDS − vDS ⎤ and vDS ≅ 0
⎣
2
⎦
1 di
So = D ≅ K n ⎡ 2 (VDD − VTN ) ⎤
⎣ ⎦
rds dvDS
Or
1
rds =
′
⎛ kn ⎞ ⎛ W ⎞
⎜ 2 ⎟ ⎜ L ⎟ ⋅ 2 (VDD − VTN )
⎝ ⎠ ⎝ ⎠n
or
1
rds =
′⎛ ⎞
W
kn ⎜ ⎟ ⋅ (VDD − VTN )
⎝L ⎠n
For vI ≅ 0, PMOS in nonsaturation
iD = K p ⎡ 2 (VDD − vI + VTP ) vSD − vSD ⎤
⎣
2
⎦
and vSD ≅ 0 for vI ≅ 0.
So
1 di ⎛ k′ ⎞⎛ W ⎞
= D ≅ ⎜ ⎟ ⎜ ⎟ ⋅ 2 (VDD + VTP )
p
rsd dvSD ⎝ 2 ⎠ ⎝ L ⎠ p
or
1
rsd =
1 ⎛W ⎞
⎜
⎜ Lp ⎟ ⋅ (VDD + VTP )
⎟
k′
p ⎝ ⎠

21. ⎛W ⎞ ⎛W ⎞
(b) For ⎜ ⎟ = 2, ⎜ ⎟ = 4
⎝ L ⎠n ⎝ L ⎠p
1
rds = ⇒ rds = 2.38 k Ω
( 50 )( 2 )( 5 − 0.8 )
1
rsd = ⇒ rsd = 2.38 k Ω
( 25 )( 4 )( 5 − 0.8 )
⎛W ⎞
For ⎜ ⎟ = 2,.
⎝ L ⎠p
1
rsd = ⇒ rsd = 4.76 k Ω
( 25 )( 2 )( 5 − 0.8 )
Now, for NMOS:
vds 0.5
vds = id rds or id = = ⇒ id = 0.21 mA
rds 2.38
For PMOS:
For rsd = 2.38 k Ω,
vsd 0.5
id = = ⇒ id = 0.21 mA
rsd 2.38
For rsd = 4.76 k Ω ,
vsd 0.5
id = = ⇒ id = 0.105 mA
rsd 4.76
16.45
From Equation (16.63)
3
VIL = 1.5 + ⋅ (10 − 1.5 − 1.5 ) ⇒ VIL = 4.125 V
8
and Equation (16.62)
1
V0 HU = ⋅ ⎡ 2 ( 4.125 ) + 10 − 1.5 + 1.5⎤
2 ⎣ ⎦
or V0 HU = 9.125 V
From Equation (16.69)
5
VIH = 1.5 + ⋅ (10 − 1.5 − 1.5 ) ⇒ VIH = 5.875 V
8
and Equation (16.68)
1
V0 LU = ⋅ ⎡ 2 ( 5.875 ) − 10 − 1.5 + 1.5⎤
2 ⎣ ⎦
or V0 LU = 0.875 V
Now
NM L = VIL − V0 LU = 4.125 − 0.875 ⇒ NM L = 3.25 V
NM H = V0 HU − VTH = 9.125 − 5.875 ⇒ NM H = 3.25 V
16.46
From Equation (16.71)
⎡ 100 ⎤
(10 − 1.5 − 1.5 ) ⎢
⎢
⎥
50 − 1 ⎥ = 1.5 + 7 ⎡ 2 ( 0.632 ) − 1⎤
VIL = 1.5 + 2 ⎣ ⎦
⎛ 100 ⎞
− 1⎟ ⎢ 100 + 3 ⎥
⎜ ⎢ 50 ⎥
⎝ 50 ⎠ ⎣ ⎦

22. or
VIL = 3.348 V
From Equation (16.70)
1 ⎧⎛ 100 ⎞ ⎛ 100 ⎞ ⎫
V0 HU = ⋅ ⎨⎜1 + ⎟ ( 3.348 ) + 10 − ⎜ ⎟ (1.5 ) + 1.5⎬
2 ⎩⎝ 50 ⎠ ⎝ 50 ⎠ ⎭
or V0 HU = 9.272 V
From Equation (16.77)
⎡ ⎛ 100 ⎞ ⎤
⎢ 2⎜ ⎟ ⎥
(10 − 1.5 − 1.5 ) ⎢ ⎝ 50 ⎠
VIH = 1.5 + − 1⎥ = 1.5 + 7 [1.51 − 1]
⎛ 100 ⎞ ⎢ ⎛ 100 ⎞ ⎥
⎜ − 1⎟ ⎢ 3 ⎜ ⎟ +1 ⎥
⎝ 50 ⎠ ⎢ ⎝ 50 ⎠
⎣ ⎥
⎦
or
VIH = 5.07 V
From Equation (16.76)
( 5.07 ) ⎛1 + ⎞ − 10 − ⎛ ⎞ (1.5 ) + 1.5
100 100
⎜ ⎟ ⎜ ⎟
V0 LU = ⎝ 50 ⎠ ⎝ 50 ⎠
⎛ 100 ⎞
2⎜ ⎟
⎝ 50 ⎠
or V0 LU = 0.9275 V
Now NM L = VIL − V0 LU = 3.348 − 0.9275
or NM L = 2.42 V
NM H = V0 HU − VIH = 9.272 − 5.07
or NM H = 4.20 V
16.47
(a)
Kn = KP
3
VIL = VTN + (VDD + VTP − VTN )
8
3
= 0.4 + ( 3.3 − 0.4 − 0.4 ) ⇒ VIL = 1.3375 V
8
1
VOHu = {2 (1.3375 ) + 3.3 − 0.4 + 0.4}
2
VOHu = 2.9875 V
5
VIH = 0.4 + ( 3.3 − 0.4 − 0.4 ) ⇒ VIH = 1.9625 V
8
1
VOLu =
2
{2 (1.9625) − 3.3 − 0.4 + 0.4}
VOLu = 0.3125 V
NM H = VOHu − VIH = 2.9875 − 1.9625 ⇒ NM H = 1.025 V
NM L = VIL − VOLu = 1.3375 − 0.3125 ⇒ NM L = 1.025 V
(b)

23. ⎡ 2 ( 4) ⎤
⎢
( 3.3 − 0.4 − 0.4 ) ⎢ ⎥
12 2.5
VIL = 0.4 + 2 − 1⎥ = 0.4 + ⎡( −0.147 ) ⎤
⎛ ( 2 )( 4 ) ⎞ ⎢ 2 ( 4)
+3 ⎥
⎥ ( −0.333) ⎣ ⎦
⎜ − 1⎟ ⎢
⎝ 12 ⎠ ⎣ 12 ⎦
VIL = 1.505 V
1 ⎧⎛ ( 2 )( 4 ) ⎞
⎪ ⎛ 2 ( 4) ⎞ ⎫
⎪ 1
VOHu = ⎨⎜1 + ⎟ (1.505 ) + 3.3 − ⎜ ⎟ ( 0.4 ) + 0.4 ⎬ = {2.5083 + 3.3 − 0.2667 + 0.4}
2 ⎪⎝
⎩ 12 ⎠ ⎝ 12 ⎠ ⎪ 2
⎭
VOHu = 2.9708 V
⎡ ⎛ 2 ( 4) ⎞ ⎤
⎢ 2⎜ ⎟ ⎥
( 3.3 − 0.4 − 0.4 ) ⎢ ⎝ 12 ⎠ 2.5
VIH = 0.4 + − 1⎥ = 0.4 + [ −0.2302] ⇒ VIH = 2.1282 V
⎛ 2 ( 4) ⎞ ⎢ ⎥ ( −0.333)
− 1⎟ ⎢ 3
( 2 )( 4 ) + 1 ⎥
⎜
⎝ 12 ⎠ ⎢ ⎣ 12 ⎥
⎦
⎛ 2 ( 4) ⎞ ⎛ 2 ( 4) ⎞
( 2.1282 ) ⎜1 + ⎟ − 3.3 − ⎜ ⎟ ( 0.4 ) + 0.4
⎝ 12 ⎠ ⎝ 12 ⎠ 3.547 − 3.3 − 0.2667 + 0.4
VOLu = = ⇒ VOLu = 0.2853 V
⎛ 2 ( 4) ⎞ 1.333
2⎜ ⎟
⎝ 12 ⎠
NM H = VOHu − VIH = 2.9708 − 2.1282 ⇒ NM H = 0.8426 V
NM L = VIL − VOLu = 1.505 − 0.2853 ⇒ NM L = 1.22 V
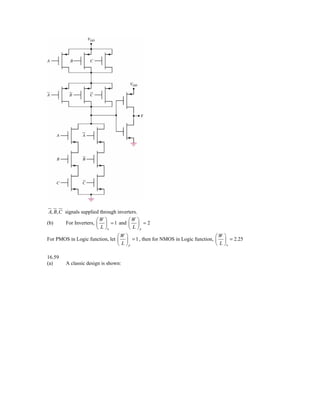
16.48
a. v A = vB = 5 V
N1 and N 2 on, so vDS1 ≈ vDS 2 ≈ 0 V
P and P2 off
1
So we have a P3 − N 3 CMOS inverter. By symmetry, vC = 2.5 V (Transition Point).
b. For v A = vB = vC ≡ vI
Want K n ,eff = K p ,eff
′
kn ⎛ W ⎞ k ′ ⎛ 3W ⎞
⋅⎜ ⎟ = P ⋅⎜ ⎟
2 ⎝ 3L ⎠ n 2 ⎝ L ⎠ P
′ ′
With kn = 2k P , then
2 1 ⎛W ⎞ 1 ⎛W ⎞
⋅ ⋅⎜ ⎟ = ⋅3⋅⎜ ⎟
2 3 ⎝ L ⎠n 2 ⎝ L ⎠ P
⎛W ⎞ 9 ⎛W ⎞
Or ⎜ ⎟ = ⋅ ⎜ ⎟
⎝ L ⎠n 2 ⎝ L ⎠ P
c. We have
⎛ k ′ ⎞ ⎛ W ⎞ ⎛ 2k ′ ⎞ ⎛ 9 ⎞ ⎛ W ⎞
Kn = ⎜ n ⎟ ⎜ ⎟ = ⎜
p
⎟⎜ ⎟⎜ ⎟
⎝ 2 ⎠ ⎝ L ⎠n ⎝ 2 ⎠ ⎝ 2 ⎠ ⎝ L ⎠ p
⎛ k′ ⎞⎛ W ⎞
Kp = ⎜ ⎟⎜ ⎟
p
⎝ 2 ⎠⎝ L ⎠p
Then from Equation (16.55)

24. Kn
5 + ( −0.8 ) + ⋅ ( 0.8 )
Kp
VIt =
Kn
1+
Kp
Now
Kn ⎛9⎞
= ( 2) ⎜ ⎟ = 9
Kp ⎝ 2⎠
Then
5 + ( −0.8 ) + 3 ( 0.8 )
VIt = ⇒ VIt = 1.65 V
1+ 3
16.49
By definition, NMOS is on if gate voltage is 5 V and is off if gate voltage is 0 V.
State N1 N2 N3 N4 N5 v0
1 off on off on on 0
2 off off on on off 0
3 on on off off on 5
4 on on off on on 0
Logic function ( v X OR vY ) ⊗ ( v X AND vZ )
Exclusive OR of ( vX OR vY ) with ( vX AND vZ )
16.50
⎛W ⎞
NMOS in Parallel ⇒ ⎜ ⎟ = 2
⎝ L ⎠n
⎛W ⎞
4-PMOS in series ⇒ ⎜ ⎟ = 4 ( 4 ) = 16
⎝ L ⎠p
(b) CL doubles ⇒ current must double to maintain switching speed.
⎛W ⎞
⇒⎜ ⎟ =4
⎝ L ⎠n
⎛W ⎞
⎜ ⎟ = 32
⎝ L ⎠p
16.51
⎛W ⎞
4-NMOS in series ⎜ ⎟ = 4 ( 2 ) = 8
⎝ L ⎠n
⎛W ⎞
4-PMOS in parallel ⎜ ⎟ = 4
⎝ L ⎠p
⎛W ⎞
(b) ⎜ ⎟ = 16
⎝L ⎠n
⎛W ⎞
⎜ ⎟ =8
⎝L ⎠p
16.52

25. ⎛W ⎞
(a) NMOS in parallel ⇒ ⎜ ⎟ = 2
⎝ L ⎠n
⎛W ⎞
3-PMOS in series ⇒ ⎜ ⎟ = 3 ( 4 ) = 12
⎝ L ⎠P
⎛W ⎞
(b) ⎜ ⎟ =4
⎝L ⎠n
⎛W ⎞
⎜ ⎟ = 24
⎝L ⎠p
16.53
⎛W ⎞
(a) 3-NMOS in series ⎜ ⎟ = 3 ( 2 ) = 6
⎝ L ⎠n
⎛W ⎞
3-PMOS in parallel ⎜ ⎟ = 4
⎝ L ⎠p
⎛W ⎞
(b) ⎜ ⎟ = 12
⎝L ⎠n
⎛W ⎞
⎜ ⎟ =8
⎝L ⎠p
16.54
(a) Y = A( B + C )( D + E )
(b)
⎛W ⎞
(c) For NMOS in pull down mode, 3 in series ⇒ ⎜ ⎟ = 3 ( 2 ) = 6
⎝ L ⎠n
For PMOS
⎛W ⎞
⎜ ⎟ =4
⎝ L ⎠P, A
⎛W ⎞
⎜ ⎟ = 2 ( 4) = 8
⎝ L ⎠ P , B ,C , D , E

26. 16.55
(a) Y = A( BD + CE )
(b)
(c) NMOS: 3 transistors in series for pull down mode.
⎛W ⎞
For twice the speed: ⎜ ⎟ = 2 ( 3)( 2 ) = 12
⎝ L ⎠n
⎛W ⎞
PMOS: ⎜ ⎟ = 2 ( 4 ) = 8
⎝ L ⎠P, A
⎛W ⎞
⎜ ⎟ = 2 ( 2 )( 4 ) = 16
⎝ L ⎠ P , B ,C , D , E
16.56
(a) Y = A + BC + DE
(b)
⎛W ⎞ ⎛W ⎞
(c) NMOS: ⎜ ⎟ = 2 ⎜ ⎟ =4
⎝ L ⎠n, A ⎝ L ⎠ n , B ,C , D , E
PMOS: 3 transistors in series for the pull-up mode

27. ⎛W ⎞
⎜ ⎟ = 3 ( 4 ) = 12
⎝ L ⎠p
16.57
(a) Y = A + ( B + D)(C + E )
(b)
⎛W ⎞ ⎛W ⎞
(c) NMOS: ⎜ ⎟ = 2 ( 2 ) = 4 ⎜ ⎟ = ( 2 )( 4 ) = 8
⎝ L ⎠n, A ⎝ L ⎠ n , B ,C , D , E
PMOS:
⎛W ⎞
⎜ ⎟ = ( 2 ) 3 ( 4 ) = 24
⎝ L ⎠p
16.58
(a) A classic design is shown:

28. A, B, C signals supplied through inverters.
⎛W ⎞ ⎛W ⎞
(b) For Inverters, ⎜ ⎟ = 1 and ⎜ ⎟ = 2
⎝ L ⎠n ⎝ L ⎠p
⎛W ⎞ ⎛W ⎞
For PMOS in Logic function, let ⎜ ⎟ = 1 , then for NMOS in Logic function, ⎜ ⎟ = 2.25
⎝ L ⎠p ⎝ L ⎠n
16.59
(a) A classic design is shown:

29. ⎛W ⎞ ⎛W ⎞
(b) ⎜ ⎟ = 1, ⎜ ⎟ =2
⎝ L ⎠ ND ⎝ L ⎠ NA, NB , NC
⎛W ⎞ ⎛W ⎞
⎜ ⎟ = 8, ⎜ ⎟ =4
⎝ L ⎠ PA, PB ⎝ L ⎠ PC , PD
16.60
( A OR B ) AND C
16.61
⎛W ⎞
5-NMOS in series ⇒ ⎜ ⎟ = 5 ( 2 ) = 10
⎝ L ⎠n
⎛W ⎞
5-PMOS in parallel ⇒ ⎜ ⎟ = 4
⎝ L ⎠p
16.62
By definition:
NMOS off if gate voltage = 0
NMOS on if gate voltage = 5 V
PMOS off if gate voltage = 5 V
PMOS on if gate voltage = 0
State N1 P1 NA NB NC v01 N2 P2 v02
1 off on off off off 5 on off 0
2 on off on off off 5 on off 0

30. 3 off on off off off 5 on off 0
4 on off off off on 5 on off 0
5 off on off off off 5 on off 0
6 on off off on on 0 off on 5
Logic function is
v02 = ( v A OR vB ) AND vC
16.63
State v01 v02 v03
1 5 5 0
2 0 0 5
3 5 5 0
4 5 0 5
5 5 5 0
6 0 5 0
Logic function:
v03 = ( vX OR vZ ) AND vY
16.64

31. 16.65

32. 16.66

33. 16.67
dVC
2 I = −C
dt
So
1
ΔVC = − ( 2I ) ⋅ t
C
For ΔVC = −0.5 V

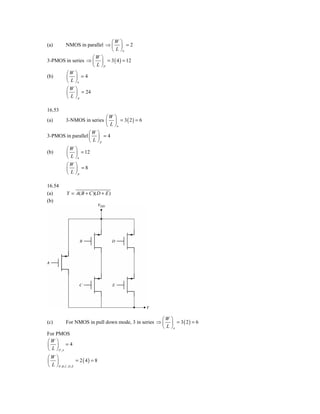
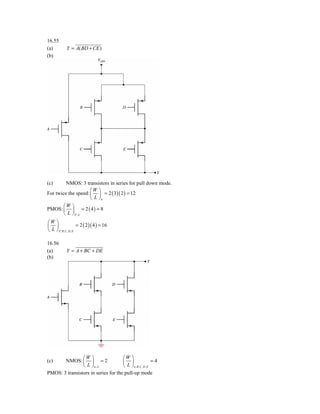
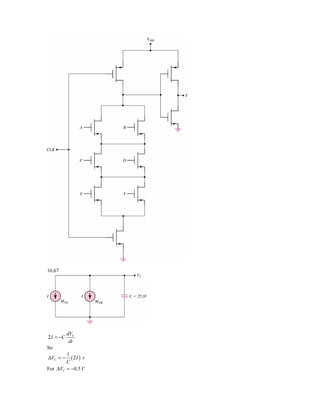
34. 2 ( 2 x 10−12 ) ⋅ t
−0.5 = − ⇒ t = 3.125 ms
25 x 10−15
16.68
(a)
(i) vO = 0
(ii) vO = 4.2 V
(iii) vO = 2.5 V
(b)
(i) vO = 0
(ii) vO = 3.2 V
(iii) vO = 2.5 V
16.69
(a)
(i) vo = 0
(ii) vo = 2.9 V
(iii) vo = 2.4 V
(b)
(i) vo = 0
(ii) vo = 2.0 V
(iii) vo = 2.0 V
16.70
Neglect the body effect.
a. v01 (logic 1) = 4.2 V , v02 (logic 1) = 5 V
b. vI = 5 V ⇒ vGS 1 = 4.2 V
M 1 in nonsaturation and M 2 in saturation. From Equation (16.23)
⎛W ⎞ ⎛W ⎞
⎟ ⎡ 2 ( vGS 1 − VTND ) vO1 − vO1 ⎤ = ⎜ ⎟ (VDD − vO1 − VTNL )
2 2
⎜ ⎣ ⎦
⎝L ⎠D ⎝ L ⎠L
⎛W ⎞ ⎡
⎟ ⎣ 2 ( 4.2 − 0.8 )( 0.1) − ( 0.1) ⎤ = (1) [5 − 0.1 − 0.8]
2 2
⎜ ⎦
⎝L ⎠D
Or
⎛W ⎞ ⎛W ⎞
⎜ ⎟ ( 0.67 ) = 16.81 ⇒ ⎜ ⎟ = 25.1
⎝L ⎠D ⎝ L ⎠D
Now
v01 = 4.2 V ⇒ vGS 3 = 4.2 V
M 3 in nonsaturation and M 4 in saturation. From Equation (16.29(b)).
⎛W ⎞ ⎛W ⎞
⎟ ⎡ 2 ( vGS 3 − VTND ) vO 2 − vO 2 ⎤ = ⎜ ⎟ [ −VTNL ]
2 2
⎜ ⎣ ⎦
⎝L ⎠D ⎝ L ⎠L
⎛W ⎞
⎟ ⎡ 2 ( 4.2 − 0.8 )( 0.1) − ( 0.1) ⎤ = ( 2 ) ⎡ − ( −1.5 ) ⎤
2 2
⎜ ⎣ ⎦ ⎣ ⎦
⎝L ⎠D
⎛W ⎞
⎜ ⎟ (0.67) = 2.25
⎝ L ⎠D

35. ⎛W ⎞
Or ⎜ ⎟ = 3.36
⎝ L ⎠D
16.71
A B Y
0 0 1
0 1 0
1 0 0
1 1 0.1 ⇒ indeterminate
Without the top transistor, the circuit performs the exclusive-NOR function.
16.72
A A B B Y Z
0 1 0 1 0 1
0 1 1 0 1 0
1 0 0 1 1 0
1 0 1 0 1 0
Y = A + AB = A + B
Z = Y or Z = AB
16.73
16.74
For φ = 1, φ = 0, then Y = B. And for φ = 0, φ = 1, then Y = A .
A multiplexer.
16.75
Y = AC + BC
16.76
Y = AB + AB = A ⊗ B
16.77

36. A B Y
0 0 0
1 0 1
0 1 1
1 1 0
Exclusive-OR function.
16.78
This circuit is referred to as a two-phase ratioed circuit. The same width-to-length ratios between the driver
and load transistors must be maintained as discussed previously with the enhancement load inverter.
When φ1 is high, v01 becomes the complement of vI . When φ2 goes high, then v0 becomes the
complement of v01 or is the same as vI . The circuit is a shift register.
16.79
Let Q = 0 and Q = 1 ; as S increases, Q decreases. When Q reaches the transition point of the M 5 − M 6
inverter, the flip-flop with change state. From Equation (16.28(b)),
KL
VIt = ⋅ ( −VTNL ) + VTND
KD
where K L = K 6 and K D = K 5 .
Then
30
VIt = ⋅ ⎡ − ( −2 ) ⎤ + 1 ⇒ VIt = Q = 2.095 V
100 ⎣ ⎦
This is the region where both M 1 and M 3 are biased in the saturation region. Then
K3 30
S= ⋅ ( −VTNL ) + VTND = ⋅ ⎡ − ( −2 ) ⎤ + 1
K1 200 ⎣ ⎦
or S = 1.77 V
This analysis neglects the effect of M 2 starting to turn on at the same time.
16.80
Let vY = R, v X = S , v02 = Q, and v01 = Q. Assume VThN = 0.5 V and VThP = −0.5 V. For S = 0, we have
the following:

37. If we want the switching to occur for R = 2.5 V, then because of the nonsymmetry between the two
circuits, we cannot have Q and Q both equal to 2.5 V.
Set R = Q = 2.5 V and assume Q goes low.
For the M 1 − M 5 inverter, M 1 in nonsaturation and M 5 in saturation. Then
K n ⎡ 2 ( 2.5 − 0.5 ) Q − Q ⎤ = K p [ 2.5 − 0.5]
2 2
⎢
⎣ ⎥
⎦
Or
2 ⎛ Kp ⎞
4Q − Q = 4 ⎜ ⎟
⎝ Kn ⎠
For the other circuit, M 2 − M 4 in saturation and M 6 in nonsaturation. Then
2
⎣ ( )
K n ( 2.5 − 0.5 ) + K n (Q − 0.5) 2 = K p ⎡ 2 5 − Q − 0.5 ( 2.5 ) − ( 2.52 ) ⎤
⎦
Combining these equations and neglecting the Q 3 term, we find
Kp
Q = 1.4 V and = 0.9
kn
16.81
3.3 + ( −0.4 ) + 0.5
vIt = = 1.7 V
1+1
vI = 1.5 V NMOS Sat; PMOS Non Sat
= ⎡ 2 ( 3.3 − vI − 0.4 )( 3.3 − vo1 ) − ( 3.3 − vo1 ) ⎤ ⇒ vo1 = 2.88 V
( vI − 0.5)
2 2
⎣ ⎦
vI = 1.6 V vo1 = 2.693 V
vI = 1.7 V vo1 = variable (switching region)
vI = 1.8 V NMOS Non Sat; PMOS Sat
( 3.3 − VI − 0.4 ) = ⎡ 2 ( vI − 0.5 ) vo1 − vo1 ⎤ ⇒ vo1 = 0.607 V
2 2
⎣ ⎦
Now
vI = 1.5 V, vo1 = 2.88 V ⇒ vo ≈ 0V
vI = 1.6 V, vo1 = 2.693 V
NMOS Non Sat; PMOS Sat
( 3.3 − vo1 − 0.4 ) = ⎡ 2 ( vo1 − 0.5 ) vo − vo2 ⎤
2
⎣ ⎦
vo = 0.00979 V
vI = 1.7 V, v o1 = Switching Mode ⇒ v0 = Switching Mode.
vI = 1.8 V, vo1 = 0.607 V NMOS Sat; PMOS Non Sat
( v01 − 0.5) = ⎡ 2 ( 3.3 − v01 − 0.4 )( 3.3 − v0 ) − ( 3.3 − v0 ) ⎤ ⇒ v0 = 3.298 V
2 2
⎣ ⎦
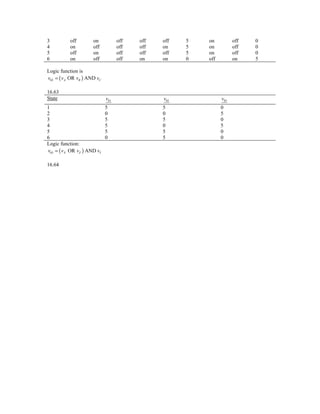
16.82
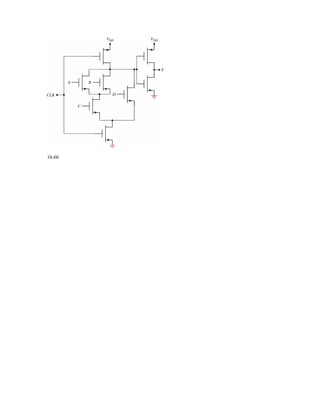
For R = φ = VDD and S = 0 ⇒ Q = 0, Q = 1
For S = φ = VDD and R = 0 ⇒ Q = 1, Q = 1
The signal φ is a clock signal.
For φ = 0, The output signals will remain in their previous state.
16.83
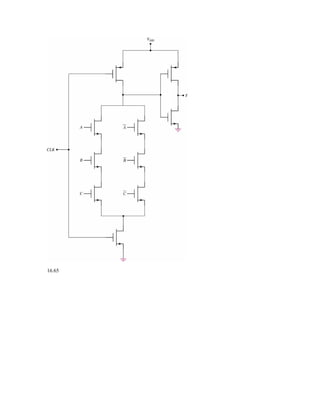
a. Positive edge triggered flip-flop when CLK = 1, output of first inverter is D and then Q = D = D .

38. b. For example, put a CMOS transmission gate between the output and the gate of M 1 driven by a
CLK pulse.
16.84
For J = 1, K = 0, and CLK = 1; this makes Q = 1 and Q = 0 .
For J = 0, K = 1, and CLK = 1 , and if Q = 1, then the circuit is driven so that Q = 0 and Q = 1.
If initially, Q = 0, then the circuit is driven so that there is no change and Q = 0 and Q = 1.
J = 1, K = 1, and CLK = 1, and if Q = 1, then the circuit is driven so that Q = 0.
If initially, Q = 0 , then the circuit is driven so that Q = 1.
So if J = K = 1, the output changes state.
16.85
For J = v X = 1, K = vY = 0, and CLK = vZ = 1, then v0 = 0.
For J = v X = 0, K = vY = 1, and CLK = vZ = 1, then v0 = 1.
Now consider J = K = CLK = 1. With v X = vZ = 1, the output is always v0 = 0, So the output does not
change state when J = K = CLK = 1. This is not actually a J − K flip-flop.
16.86
64 K ⇒ 65,536 transistors arranged in a 256 × 256 array.
(a) Each column and row decoder required 8 inputs.
(b)
(i) Address = 01011110 so input = a7 a6 a5 a4 a3 a2 a1a0
(ii) Address = 11101111 so input = a7 a6 a5 a4 a3 a2 a1a0
(c)
(i) Address = 00100111 so input = a7 a6 a5 a4 a3 a2 a1a0
(ii) Address = 01111011 so input = a7 a6 a5 a4 a3 a2 a1a0
16.87
(a) 1-Megabit memory ⇒
= 1, 048,576 ⇒ 1024 × 1024
Nuclear & input row and column decodes lines necessary = 10
(b) 250K × 4 bits ⇒ 262,144 × 4 bits ⇒ 512 × 512
For 512 lines ⇒ 9 row and column decoder lines necessary.
16.88
Put 128 words in a 8 × 16 array, which means 8 row (or column) address lines and 16 column (or row)
address lines.
16.89
Assume the address line is initially uncharged, then
dV 1 I
I = C C or VC = ∫ Idt = ⋅ t
dt C C
VC ⋅ C ( 2.7 ) ( 5.8 × 10 )
−12
Then t = = ⇒
I 250 × 10−6
t = 6.26 × 10 −8 s ⇒ 62.6 ns
16.90

39. 5 − 0.1 ⎛ 35 ⎞⎛ W ⎞⎡
⎟ ⎣ 2 ( 5 − 0.7 )( 0.1) − ( 0.1) ⎤
2
(a) = ⎜ ⎟⎜
1 ⎝ 2 ⎠⎝ L ⎠ ⎦
⎛W ⎞
or ⎜ ⎟ = 0.329
⎝L ⎠
(b) 16 K ⇒ 16,384 cells
2
iD ≅ = 2 μA
1
Power per cell = (2 μ A)(2 V ) = 4 μW
Total Power = PT = (4 μW )(16,384) ⇒ PT = 65.5 mW
Standby current = (2 μ A)(16,384) ⇒ IT = 32.8 mA
16.91
16 K ⇒ 16,384 cells
200
PT = 200 mW ⇒ Power per cell = ⇒ 12.2 μW
16,384
P 12.2 V 2.5
iD = = = 4.88 μ A ≅ DD = ⇒ R = 0.512 M Ω
VDD 2.5 R R
If we want vO = 0.1 V for a logic 0, then
⎛ k′ ⎞⎛ W ⎞
iD = ⎜ n ⎟ ⎜ ⎟ ⎡ 2 (VDD − VTN ) vO − vO ⎤
2
⎝ 2 ⎠⎝ L ⎠ ⎣ ⎦
⎛ 35 ⎞ ⎛ W ⎞
4.88 = ⎜ ⎟ ⎜ ⎟ ⎡ 2 ( 2.5 − 0.7 )( 0.1) − ( 0.1) ⎤
2
⎝ 2 ⎠⎝ L ⎠ ⎣ ⎦
⎛W ⎞
So ⎜ ⎟ = 0.797
⎝L⎠
16.92
Q = 0, Q = 1
So D = Logic 1 = 5 V
A very short time after the row has been addressed, D remains charged at VDD = 5 V . Then M p 3, M A, and
M N 1 begin to conduct and D decreases. In steady-state, all three transistors are biased in the nonsaturation
region. Then
K p 3 ⎡ 2 (VSG 3 + VTP 3 ) VSD 3 − VSD 3 ⎤ = K nA ⎡ 2 (VGSA − VTNA ) VDSA − VDSA ⎤ = K n1 ⎡ 2 (VGS 1 − VTN 1 ) VDS 1 − VDS 1 ⎤
⎣
2
⎦ ⎣
2
⎦ ⎣
2
⎦
Or
K p 3 ⎡ 2 (VDD + VTP 3 )(VDD − D ) − (VDD − D ) ⎤ = K nA ⎡ 2 (VDD − Q − VTNA )( D − Q ) − ( D − Q ) ⎤
2 2
⎣ ⎦ ⎣ ⎦
= K n1 ⎡ 2 (VDD − VTN 1 ) Q − Q 2 ⎤ (1)
⎣ ⎦
Equating the first and third terms:
⎛ 20 ⎞ ⎡ ⎤ ⎛ 40 ⎞
⎜ ⎟ (1) ⎣ 2 ( 5 − 0.8 )( 5 − D ) − ( 5 − D ) ⎦ = ⎜ ⎟ ( 2 ) ⎣ 2 ( 5 − 0.8 ) Q − Q ⎦ (2)
2
⎡ 2
⎤
⎝ 2 ⎠ ⎝ 2 ⎠
As a first approximation, neglect the ( 5 − D ) and Q 2 terms. We find
2
Q = 1.25 − 0.25 D (3)
Then, equating the first and second terms of Equation (1):
⎛ 20 ⎞ ⎡ ⎛ 40 ⎞
⎜ ⎟ (1) ⎣ 2 ( 5 − 0.8 )( 5 − D ) − ( 5 − D ) ⎤ = ⎜ ⎟ (1) ⎡ 2 ( 5 − Q − 0.8 )( D − Q ) − ( D − Q ) ⎤
2 2
⎝ 2 ⎠ ⎦ ⎝ 2 ⎠ ⎣ ⎦

40. Substituting Equation (3), we find as a first approximation: D = 2.14 V
Substituting this value of D into equation (2), we find
8.4 ( 5 − 2.14 ) − ( 5 − 2.14 ) = 4 ⎡8.4Q − Q 2 ⎤
2
⎣ ⎦
We find Q = 0.50 V
Using this value of Q, we can find a second approximation for D by equating the second and third terms of
equation (1). We have
20 ⎡ 2 ( 4.2 − Q )( D − Q ) − ( D − Q ) ⎤ = 40 ⎡ 2 ( 4.2Q ) − Q 2 ⎤
2
⎣ ⎦ ⎣ ⎦
Using Q = 0.50 V , we find D = 1.79 V
16.93
Initially M N 1 and M A turn on.
M N 1, Nonsat; M A , sat.
K nA [VDD − Q − VTN ] = K n1 ⎡ 2 (VDD − VTN 1 ) Q − Q 2 ⎤
2
⎣ ⎦
⎛ 40 ⎞ ⎛ 40 ⎞
⎜ ⎟ (1) [5 − Q − 0.8] = ⎜ ⎟ ( 2 ) ⎣ 2 ( 5 − 0.8 ) Q − Q ⎦
2
⎡ 2
⎤
⎝ 2 ⎠ ⎝ 2 ⎠
which yields
Q = 0.771 V
Initially M P 2 and M B turn on
Both biased in nonsaturation reagion
( ) ( )
K P 2 ⎡ 2 (VDD + VTP 3 ) VDD − Q − VDD − Q ⎤ = K nB ⎡ 2 (VDD − VTNB ) Q − Q ⎤
2 2
⎢
⎣ ⎥
⎦ ⎢
⎣ ⎥
⎦
⎛ 20 ⎞ ⎤ ⎛ 40 ⎞ ⎡
⎡
( ) ( ) ⎤
2 2
⎜ ⎟ ( 4 ) ⎢ 2 ( 5 − 0.8 ) 5 − Q − 5 − Q ⎥ = ⎜ ⎟ (1) ⎢ 2 ( 5 − 0.8 ) Q − Q ⎥
⎣ ⎦ ⎝ 2 ⎠ ⎣ ⎦
⎝ 2 ⎠
which yields Q = 3.78 V
Note: (W / L) ratios do not satisfy Equation (16.86)
16.94
For Logic 1, v1:
( 5 )( 0.05 ) + ( 4 )(1) = (1 + 0.05 ) v1 ⇒ v1 = 4.0476 V
v2 :
(5)(0.025) + (4)(1) = (1 + 1.025)v2 ⇒ v2 = 4.0244 V
For Logic 0, v1:
(0)(0.05) + (4)(1) = (1 + 0.05)v1 ⇒ v1 = 3.8095 V
v2 :
(0)(0.025) + (4)(1) = (1 + 0.025)v2 ⇒ v2 = 3.9024 V
16.95
Not given
16.96
Not given
16.97
Not given

41. 16.98
1
(a) Quantization error = LSB ≤ 1% ≤ 0.05 V
2
Or LSB ≤ 0.10 V
5
For a 6-bit word , LSB = = 0.078125 V
64
5
(b) 1 − LSB = = 0.078125 V
64
3.5424
(c) × 64 = 45.34 ⇒ n = 45
5
Digital Output = 101101
45 × 5
= 3.515625
64
.
1
Δ = 3.5424 − 3.515625 = 0.026775 < LSB.
2
16.99
1
(a) Quantization error = LSB ≤ 0.5% ≤ 0.05 V
2
1 − LSB = 0.10 V
10
For a 7-beit word, LSB = = 0.078125 V
128
(b) 1 − LSB = 0.078125 V
3.5424
(c) ×128 = 45.34272 ⇒ n = 45
10
Digital output = 0101101
45 × 10
Now = 3.515625
128
1
Δ = 3.5424 − 3.515625 = 0.026775 V < LSB
2
16.100
⎛0 1 0 1 ⎞
(a) vo = ⎜ + + + ⎟ ( 5 )
⎝ 2 4 8 16 ⎠
vo = 1.5625 V
⎛1 0 1 0 ⎞
(b) vo = ⎜ + + + ⎟ ( 5 )
⎝ 2 4 8 16 ⎠
vo = 3.125 V
16.101
⎛1⎞
(a) LSB = ⎜ ⎟ ( 5 ) = 0.3125 V
⎝ 16 ⎠
1
LSB = 0.15625 V
2
⎛ 10 ⎞
Now vo = ⎜ ⎟ (5)
⎝ 20 + ΔR1 ⎠

42. For vo = 2.5 + 0.15625 = 2.65625 V
(10 )( 5)
20 + ΔR1 = ⇒ ΔR1 = −1.176 K
2.65625
For vo = 2.5 − 0.15625 = 2.34375 V
(10 )( 5 )
20 + ΔR1 =
2.34375 V
ΔR1 = +1.333 K
For ΔR1 = 1.176 K ⇒ ΔR1 = 5.88%
⎛ 10 ⎞
(b) For R4 : vo = ⎜ ⎟ ( 5)
⎝ 160 + ΔR4 ⎠
vo = 0.3125 + 0.15625 = 0.46875 V
(10 )( 5 )
160 + ΔR4 = ⇒ ΔR4 = −53.33K
0.46875
Or vo = 0.3125 − 0.15625 = 0.15625 V
(10 )( 5 )
160 + ΔR4 = ⇒ ΔR4 = 160 K
0.15625
For ΔR4 = 53.33K ⇒ ΔR4 = 33.33%
16.102
(a) R5 = 320 kΩ
R6 = 640 kΩ
R7 = 1280 kΩ
R8 = 2560 kΩ
⎛ 10 ⎞
(b) vo = ⎜ ⎟ ( 5 ) = 0.01953125 V
⎝ 2560 ⎠
16.103
(a)
V −5
I1 = REF = ⇒ I1 = −0.50 mA
2 R 10
I
I 2 = 1 = −0.25 mA
2
I2
I 3 = = −0.125 mA
2
I3
I 4 = = −0.0625 mA
2
I4
I 5 = = −0.03125 mA
2
I
I 6 = 5 = −0.015625 mA
2
(b) Δvo = I 6 RF = ( 0.015625 )( 5 )
Δvo = 0.078125 V
(c) vo = − [ I 2 + I 5 + I 6 ] RF = [ 0.25 + 0.03125 + 0.015625] ( 5 )
vo = 1.484375 V

43. (d) For 101010; vo = ( 0.50 + 0.125 + 0.03125 )( 5 ) = 3.28125 V
For 010101; vo = ( 0.25 + 0.0625 + 0.015625 )( 5 ) = 1.640625 V
Δvo = 1.640625 V
16.104
1 ⎛V ⎞⎛ R ⎞ V 5
LSB = ⎜ REF ⎟ ⎜ ⎟ = REF = = 0.3125 V
2 ⎝ 8 R ⎠ ⎝ 2 ⎠ 16 16
Ideal
⎛ 3V ⎞ 3
v A for 011 ⇒ ⎜ REF ⎟ ( R ) = VREF = 1.875 V
⎝ 8R ⎠ 8
1
Range of v A = 1.875 ± LSB
2
or 1.5625 ≤ vA ≤ 2.1875 V
16.105
6-bits ⇒ 26 = 64 resistors
26 − 1 = 63 comparators
16.106
(a) 10- bit output ⇒ 1024 clock periods
1 1
1 clock period = = 6 = 1 μS
f 10
May conversion time = 1024 μS = 1.024 mS
(b)
1 1⎛ 5 ⎞
LSB = ⎜ ⎟ = 0.002441406 V
2 2 ⎝ 1024 ⎠
⎛ 5 ⎞
v′ = (128 + 16 + 2 ) ⎜
A ⎟ = 0.712890625 V
⎝ 1024 ⎠
1
So range of v A = v′ ± LSB
A
2
0.710449219 ≤ v A ≤ 0.715332031 V
(c) 0100100100 ⇒ 256 + 32 + 4 = 292 clock pulses
16.107
N ×5
(a) 3.125 = ⇒ N = 640 ⇒ 512 + 128
1024
Output = 1010000000
(b)
N ×5
1.8613 = ⇒ N = 381.19 ⇒ N = 381 ⇒ 256 + 64 + 32 + 16 + 8 + 4 + 1
1024
Output = 0101111101