The document provides solutions to various problems involving the analysis and design of transistor amplifiers and power supplies. It examines concepts such as maximum power transfer, voltage gain, efficiency, heat dissipation, and voltage/current characteristics. Diagrams and calculations are presented to determine operating voltages and currents, power outputs, temperature rises, and efficiency for different circuit configurations under varying conditions.

1. Chapter 8
Problem Solutions
8.1
a.
b. i. VD D = 80 V
VD D
Maximum power at VDS = = 40 V
2
PT 25
ID = = = 0.625 A
VD S 40
80 − 40
RD = ⇒ RD = 64 Ω
0.625
ii. VD D = 50 V
VD D
Maximum power at VD S = = 25 V
2
PT 25
ID = = =1 A
VDS 25
50 − 25
RD = ⇒ RD = 25 Ω
1
8.2
a.

2. VC C
PQ (max) = I C Q ⋅
2
2 PQ (max) 2(20)
So I C Q = = = 1.67 A
VCC 24
VCC − (VCC / 2) 24 − 12
RL = = ⇒ RL = 7.2 Ω
I CQ 1.67
I CQ1.67
IB = = ⇒ 20.8 mA
β 80
24 − 0.7
RB = ⇒ RB = 1.12 kΩ
20.8
b.
I CQ ⋅ RL (1.67 )( 7.2 )
Av = g m RL = = = 462
VT 0.026
V0 (max) 12
V0 (max) = 12 V ⇒ VP = = ⇒ VP ≅ 26 mV
Av 462
8.3
VC C
a. For maximum power delivered to the load, set VC EQ =
2
Set VC C = 25 V = VCE ( sus )
VCC 25
Then I Cm = =
RL 0.1
I Cm = 250 mA < I C ,max
25 − 12.5
I CQ = = 125 mA
0.1
V
PQ ( max ) = I CQ ⋅ CC = ( 0.125 )(12.5 )
2
= 1.56 W < PD,max
125
I BQ = = 1.25 mA
100
25 − 0.7
RB = ⇒ RB = 19.4 kΩ
1.25
1 2 1
PL ( max ) = ⋅ I CQ ⋅ RL = ( 0.125 ) (100 ) ⇒ PL ( max ) = 0.781 W ( rms )
2
b.
2 2
8.4
Point (b): Maximum power delivered to load.
Point (a): Will obtain maximum signal current output.
Point (c): Will obtain maximum signal voltage output.

3. 8.5
a.
b.
VGG = 5 V, I D = 0.25 ( 5 − 4 ) = 0.25 A, VD S = 37.5 V, P = 9.375 W
2
VGG = 6 V, I D = 0.25 ( 6 − 4 ) = 1.0 A, VD S = 30 V, P = 30 W
2
VGG = 7 V, I D = 0.25 ( 7 − 4 ) = 2.25 A, VD S = 17.5 V, P = 39.375 W
2
VGG = 8 V, I D = 0.25 ⎡ 2 ( 8 − 4 )VD S − VD S ⎤
⎣
2
⎦
40 − VD S
= ⇒ VD S = 2.92
10
I D = 3.71 A, P = 10.8 W
VGG = 9 V, I D = 0.25 ⎡ 2 ( 9 − 4 ) VD S − VD S ⎤
⎣
2
⎦
40 − VD S
= ⇒ VD S = 1.88 V
10
I D = 3.81 A, P = 7.16 W
c. Yes, at VGG = 7 V, P = 39.375 W > PD ,max = 35 W
8.6
a.
VDD
Set VDSQ = = 25 V
2
50 − 25
I DQ = = 1.25 A
20
I DQ = K n (VGS − VTN )
2
1.25
+ 4 = VGS = 6.5 V
0.2
⎛ R2 ⎞
VGS = ⎜ ⎟ VDD
⎝ R1 + R2 ⎠
Let R1 + R2 = 100 kΩ
⎛ R ⎞
6.5 = ⎜ 2 ⎟ ( 50 ) ⇒ R2 = 13 kΩ
⎝ 100 ⎠
R1 = 87 kΩ
b. PD = I DQVDSQ = (1.25 )( 25 ) ⇒ PD = 31.25 W
c.
I D ,max = 2 I DQ ⇒ I D ,max = 2.5 A
VDS ,max = VDD ⇒ VDS ,max = 50 V
PD ,max = 31.25 W
d.

4. V0
= g m RL
Vi
g m = 2 K n I DQ = 2 ( 0.2 )(1.25) = 1 A / V
V0 = (1)( 20 )( 0.5 ) = 10 V
1 V02 1 (10 )
2
PL = ⋅ = ⋅ ⇒ PL = 2.5 W
2 RL 2 20
PQ = 31.25 − 2.5 ⇒ PQ = 28.75 W
8.7
(a)
(b) PD = PD ,max − ( Slope ) (T j − 25 )
60
At PD = 0, T j ,max = + 25 ⇒ T j ,max = 145°C
0.5
T j ,max − Tcase 145 − 25
(c) PD ,max = or θ dev − amb = ⇒ θ dev − amb = 2°C/W
θ dev − amb 60
8.8
T j ,max − Tamb
PD ,rated =
θ dev − case
T j ,max − Tamb
or θ dev − case =
PD ,rated
150 − 25
= = 2.5°C/W
50
Then Tdev − Tamb = PD (θ dev − case + θ case − amb )
150 − 25 = PD ( 2.5 + θ case − amb ) ⇒ 125 = PD ( 2.5 + θ case − amb )
8.9
PD = I D ⋅ VDS = ( 4 )( 5 ) = 20 W
Tdev − Tamb = PD (θ dev − case + θ case − snk + θ snk − amb )
Tdev − 25 = 20 (1.75 + 0.8 + 3) = 111 ⇒ Tdev = 136°C
Tdev − Tcase = PD ⋅θ dev − case = ( 20 )(1.75 ) = 35
Tcase = Tdev − 35 = 136 − 35 ⇒ Tcase = 101°C
Tcase − Tsink = PD ⋅θ case − snk = ( 20 )( 0.8 ) = 16°C
Tsink = Tcase − 16 = 101 − 16 ⇒ Tsink = 85°C
8.10

5. Tdev − Tamb = PD (θ dev − case + θ case − amb )
200 − 25 = 25 ( 3 + θ case − amb ) ⇒ θ case − amb = 4°C/W
8.11
T j ,max − Tamb 175 − 25
θ dev − case = = = 10°C/W
PD ,rated 15
T j ,max − Tamb
PD =
θ dev − case + θ case −snk + θ snk − amb
175 − 25
= ⇒ PD = 10 W
10 + 1 + 4
8.12
PL
η=
PS
PS = VCC ⋅ I Q
⎛V ⎞
PL = VP ⋅ I P = ⎜ CC ⎟ ( I Q )
⎝ 2 ⎠
1
⋅ VCC ⋅ I Q
η= 2 ⇒ η = 50%
VCC ⋅ I Q
8.13
vo ( max ) = 4.8 V
−0.7 − ( −5 )
iC 3 = iC 2 = = 4.3 mA
1
vS ( min )
vI = vo + 0.7 iL ( max ) = −4.3 mA =
1
so − 3.6 ≤ vI ≤ 5.5 V vo ( min ) = −4.3 V
8.14

6. 0 − VGS 3 − ( −5 )
I D 3 = K (VGS 3 − VTN ) =
2
R
12 (VGS 3 − 0.5 ) = 5 − VGS 3
2
2
2VGS 3 − 11VGS − 2 = 0
(11) + 4 (12 )( 2 )
2
11 ±
VGS 3 =
2 (12 )
VGS 3 = VGS 2 = 1.072 V
I D 3 = I D 2 = 12 (1.072 − 0.5 ) = 3.93 mA
2
VDS 2 ( sat ) = VGS 2 − VTN = 1.072 − 0.5 = 0.572 V
V0 ( min )
vo ( min ) : i2 ( max ) = −3.93 = ⇒ V0 ( min ) = −3.93 V
1
vI ( min ) = vo ( min ) + VTN = −3.93 + 0.5
vI ( min ) = −3.43 V
vo ( max ) = 5 − VDS ( sat ) = 5 − 0.572
vo ( max ) = 4.43 V
4.43
I D1 ( max ) = 3.93 + = 8.36 mA
1
I D1 = 8.36 = 12 (VGS 1 − 0.5 ) ⇒ VGS 1 = 1.33 V
2
vI ( max ) = vo + VGS1 = 4.43 + 1.33 ⇒ vI ( max ) = 5.76 V
8.15
a. Neglect base currents.
v0 ( max ) = V + − VCE (sat) = 10 − 0.2 = 9.8 V
9.8 9.8
iL (max) = I Q = = ⇒ I Q = 9.8 mA
RL 1
0 − 0.7 − ( −10 )
R= ⇒ R = 949 Ω
9.8
iE1 ( max ) = 2 I Q ⇒ iE1 ( max ) = 19.6 mA
iE1 ( min ) = 0
iL ( max ) = I Q = 9.8 mA
iL ( min ) = − I Q = −9.8 mA
b.
1 1
( iL ( max ) ) RL = 2 ( 9.8)2 (1) ⇒ PL = 48.02 mW
2
PL =
2
PS = I Q (V + − V − ) + I Q ( 0 − V − )
= 9.8 ( 20 ) + 9.8 (10 ) ⇒ PS = 294 mW
PL 48.02
η= = ⇒ η = 16.3%
PS 294
8.16
a.
v0 ( max ) 10
I Q ( min ) = = ⇒ I Q ( min ) = 100 mA
RL 0.1
0 − 0.7 − ( −12 )
R= ⇒ R = 113 Ω
100
b.

7. PQ1 = I Q ⋅ VCE1 = (100 )(12 ) ⇒ PQ1 = 1.2 W
P (source) = 2 I Q (12 ) = 2.4 W
c.
(10 )
2
1 VP2
PL = ⋅ = = 0.5 W
2 RL 2 (100 )
PS = 1.2 + 2.4 = 3.6 W
PL 0.5
η= = ⇒ η = 13.9%
PS 3.6
8.17
I D1 = K n (VGS − VTN ) = 12 ( 0 − ( −1.8 ) )
2 2
I D1 = 38.9 mA
(a)
For RL = ∞
vo ( max ) = 4.8 V
VDS ( sat ) = VGS − VTN = 1.8 V
vo ( min ) = −5 + 1.8 = −3.2 V
vI = vo + 0.7 ⇒ −2.5 ≤ vI ≤ 5.5 V
(b) For RL = 500 Ω vo ( max ) = 4.8 V
vo −3.2
For vo < 0, vo ( min ) = −3.2 V ′
I2 = = = −6.4 mA
RL 0.5
−2.5 ≤ vI ≤ 5.5 V
(c)
For vo = −2V , I 2 ( max ) = −38.9 mA
′
−2
R2 ( min ) = ⇒ RL ( min ) = 51.4 Ω
−38.9
1 v2 1 ( 2)
2
PL = ⋅ o = ⋅ ⇒ PL = 38.9 mW
2 RL 2 51.4
38.9
PL = 10 ( 38.9 ) = 389 mW % = = 10%
389
8.18
V 2 (V )
+ 2
PL = P =
RL RL
1 (V ) 1 (V )
+ 2 − 2
PS = ⋅ + ⋅ , V − = −V +
2 RL 2 RL
So PS =
(V )
+ 2
RL
PL
η= ⇒ η = 100%
PS
8.19
(a)

8. As maximum conversion efficiency
π V
η = , P = 0.785
4 VCC
⎛4⎞
So V p ( max ) = ( 0.785 )( 5 ) ⎜ ⎟
⎝π ⎠
V p ( max ) = 5 V
2VCC 2 ( 5)
(b) Maximum power dissipation occurs when V p = = = 3.183 V
π π
2
VCC
(c) P ( max ) =
θ
π RL
2
( 5)
2
2= ⇒ RL = 1.27 Ω
π 2 RL
8.20
2
1 Vp
(a) P= ⋅
2 RL
2
1 Vp
50 = ⋅ ⇒ V p = 49 V ⇒ V + = 52 V, V − = −52 V
2 24
V 49
(b) IP = P = = 2.04 A
RL 24
π VP π ⎛ 49 ⎞
(c) η= ⋅ = ⎜ ⎟
4 VCC 4 ⎝ 52 ⎠
η = 74.0%
8.21
(a)
VDS ≥ VDS ( sat ) = VGS − VTN = VGS
VDS = 10 − Vo ( max ) and I D = I L = K n (VGS )
2
Vo ( max )
= K n (VGS )
2
RL
Vo ( max )
VGS =
RL ⋅ K n
Vo ( max ) Vo ( max )
So 10 − Vo ( max ) = =
RL ⋅ K n ( 5 )( 0.4 )
2 V0 ( max )
⎡10 − V0 ( max ) ⎤ =
⎣ ⎦ 2
V0 ( max )
100 − 20V0 ( max ) + V02 ( max ) =
2
V02 ( max ) − 20.5V0 ( max ) + 100 = 0
( 20.5 ) − 4 (100 )
2
20.5 ±
V0 ( max ) = ⇒ V0 ( max ) = 8 V
2
8
iL = ⇒ iL = 1.6 mA
5
i 1.6
VGS = L = = 2 V ⇒ VI = 10 V
Kn 0.4
b.

9. 1 (8)
2
PL = ⋅ = 6.4 mW
2 5
20 (1.6 )
PS = = 10.2 mW
π
PL 6.4
η= = ⇒ η = 62.7%
PS 10.2
8.22
vO = iL RL and iL = iD = K n ( vGS − VTN ) or iL = K n ( vGS ) and vGS = vI − vO
2 2
Then
vO = K n RL ( vI − vO ) or vO = 2 ( vI − vO )
2 2
dv0 ⎛ dv ⎞
= ( 2 )( 2 )( vI − v0 ) ⎜ 1 − 0 ⎟
dvI ⎝ dvI ⎠
dv0
⎡1 + 4 ( vI − v0 ) ⎤ = 4 ( vI − v0 )
dvI ⎣ ⎦
dv0 4 ( vI − v0 )
or =
dvI 1 + 4 ( vI − v0 )
dv0 4 (10 − 8 ) dv
For vI = 10 V, v0 = 8 V ⇒ = ⇒ 0 = 0.889
dvI 1 + 4 (10 − 8 ) dvI
dv0
At vI = 0, v0 = 0 ⇒ =0
dvI
dv0
At vI = 1, v0 = 0.5 ⇒ = 0.667
dvI
8.23
a.
⎛i ⎞ ⎛ 5 × 10−3 ⎞
VBE = VT ln ⎜ C ⎟ = ( 0.026 ) ln ⎜ −13 ⎟
⎝ IS ⎠ ⎝ 5 × 10 ⎠
V
VBE = BB = 0.5987 V ⇒ VBB = 1.1973 V
2
PQ = iC ⋅ vCE = ( 5 )(10 ) ⇒ PQ = 50 mW
b.

10. v0 = −8 V
−8
iL = ⇒ iL = −80 mA
0.1
iCp ≈ 80 mA
⎛ iCp ⎞ ⎛ 80 × 10−3 ⎞
vEB = VT ln ⎜ ⎟ = ( 0.026 ) ln ⎜ −13 ⎟
⎝ IS ⎠ ⎝ 5 × 10 ⎠
vEB = 0.6708 V
VBB
vI = − vEB + v0 = 0.5987 − 0.6708 − 8⇒ vI = −8.072 V
2
VBE = VBB − vEB = 1.1973 − 0.6708 = 0.5265 V
⎛v ⎞ ⎛ 0.5265 ⎞
iCn = I S exp ⎜ BE ⎟ = 5 × 10−13 exp ⎜ ⎟ ⇒ iCn = 0.311 mA
⎝ VT ⎠ ⎝ 0.026 ⎠
PL = iL RL = ( 80 ) ( 0.1) ⇒ PL = 640 mW
2 2
PQn = iCn ⋅ vCE = ( 0.311) (10 − ( −8 ) ) ⇒ PQn = 5.60 mW
PQp = iCp ⋅ vEC = ( 80 )( 2 ) ⇒ PQp = 160 mW
8.24
iDn = K n ( vGSn − VTN )
2
(a)
0.5 V
+ 2 = vGSn = 2.5 V = BB ⇒ VBB = 5.0 V
2 2
Pn = ( 0.5 )(10 ) ⇒ Pn = Pp = 5 mW
(b) VDS = VGS − VTN ⇒ VDS = VGS − 2 VDS = 10 − vo ( max )
and
iL v ( max ) v ( max )
VGS = + VTN = O +2 = O +2
Kn RL K n ( 2 )(1)
so
v0 ( max ) v0 ( max )
10 − v0 ( max ) = +2−2 =
2 2
so v0 ( max ) = 8 V
8
iDn = iL = ⇒ iDn = iL = 8 mA
1
8
VGS = + 2 ⇒ VGS = 4 V
2
V
Then vI = vo + VGS − BB = 8 + 4 − 2.5 ⇒ vI = 9.5 V
2
⎛ VBB ⎞
vSGp = vo − ⎜ vI − ⎟ = 8 − ( 9.5 − 2.5 )
⎝ 2 ⎠
vSGp = 1 V ⇒ M p cutoff ⇒ iDp = 0
PL = iL RL = ( 8 ) (1) ⇒ PL = 64 mW
2 2
PMn = iDn ⋅ vDS = ( 8 )(10 − 8 ) ⇒ PMn = 16 mW
PMp = iDp ⋅ vSD ⇒ PMp = 0
8.25
a.

11. 24
v0 = 24 V ⇒ iL = ⇒ iL ≈ iN = 3 A
8
3
iBn = ⇒ iBn = 73.2 mA
41
For iD = 25 mA ⇒ iR1 = 25 + 73.2 = 98.2 mA
⎛i ⎞ ⎛ 3 ⎞
VBE = VT ln ⎜ N ⎟ = ( 0.026 ) ln ⎜ −12 ⎟
⎝ IS ⎠ ⎝ 6 × 10 ⎠
= 0.7004 V
30 − ( 24 + 0.7 ) 5.3
Then 98.2 = ⇒ R1 = ⇒ R1 = 53.97 Ω
R1 98.2
⎛ 25 × 10−3 ⎞
VD = ( 0.026 ) ln ⎜ −12 ⎟
= 0.5759 V
⎝ 6 × 10 ⎠
VEB = 2VD − VBE = 2 ( 0.5759 ) − 0.7004
= 0.4514 V
⎛V ⎞ ⎛ 0.4514 ⎞
iP = I S exp ⎜ EB ⎟ = ( 6 × 10−12 ) exp ⎜ ⎟ ⇒ iP = 0.208 mA
⎝ VT ⎠ ⎝ 0.026 ⎠
b. Neglecting base current
30 − 0.6 30 − 0.6
iD ≈ = ⇒ iD ≈ 545 mA
R1 53.97
⎛ 0.545 ⎞
VD = ( 0.026 ) ln ⎜ −12 ⎟
= 0.656 V
⎝ 6 × 10 ⎠
Approximation for iD is okay.
Diodes and transistors matched ⇒ iN = iP = 545 mA
8.26
(a)
I D1 = K1 (VGS 1 − VTN )
2
5
VGS1 = +1 = 2 V
5
I D 3 = K 3 (VGS 3 − VTN )
2
200 = K 3 ( 2 − 1) ⇒ K n3 = K p 4 = 200 μ A / V 2
2
(b)
vI + VSG 4 + VGS 3 − VGS1 = vO
For vo large, iL = i1 = K n1 (VGS1 − VTN )
2
iL vo
VGS1 = + VTN = + VTN
K n1 RL K n1
⎛ vo ⎞
So vI + 2 + 2 − ⎜ + 1⎟ = v0
⎜ ( 0.5)( 5) ⎟
⎝ ⎠
v0
vI = v0 + −3
2.5
dvI dv 1 1 dv
=1= 0 + ⋅ ⋅ 0
dvI dvI 2 2.5v0 dvI
⎡
dv0 1 ⎤
1= ⎢1 + ⎥
⎢ 2 2.5v0 ⎥
dvI
⎣ ⎦
For vO = 5 V :

12. dv0 ⎡ 1 ⎤ dv dv
1= ⎢1 + ⎥ = 0 (1.1414 ) ⇒ 0 = 0.876
dvI ⎢ 2 2.5 ( 5 ) ⎥ dvI dvI
⎣ ⎦
8.27
VBB I Dn
vO = vI + − VGS and VGS = + VTN
2 Kn
vO
For vO ≈ 0, I Dn = I DQ + iL = I DQ +
RL
VBB I DQ + ( vO / RL ) V I DQ v
Then vO = vI + − VTN − or vO = vI + BB − VTN − ⋅ 1+ O
2 Kn 2 Kn I DQ RL
VBB I DQ 1 v
For vO small, vO ≅ vI + − VTN − ⋅ 1+ ⋅ O
2 Kn 2 I DQ RL
⎡ 1 I DQ 1 ⎤ V I DQ
vO ⎢1 + ⋅ ⋅ ⎥ = vI + BB − VTN −
⎢ 2 Kn
⎣ I DQ RL ⎥
⎦ 2 Kn
Now
dvO 1
= = 0.95
dvI ⎡ 1 I DQ 1 ⎤
⎢1 + ⋅ ⋅ ⎥
⎢ 2
⎣ K n I DQ RL ⎥
⎦
1 I DQ 1 1
So ⋅ ⋅ = − 1 = 0.0526
2 K n I DQ RL 0.95
1
For RL = 0.1 k Ω, then = 0.01052
K n I DQ
Or K n I DQ = 95.1
We can write g m = 2 K n I DQ = 190 mA/V
This is the required transconductance for the output transistor. This implies a very large transistor.
8.28
Av = − g m RL
I CQ
So −12 = − g m ( 2 ) ⇒ g m = 6 mA/V=
VT
I CQ = ( 6 )( 0.026 ) ⇒ I CQ = 0.156 mA
VCC 10
But for maximum symmetrical swing, set I CQ = = = 5 mA ⇒ Av > 12
RL 2
Maximum power to the load:
1 VCC (10 )
2 2
PL ( max ) = ⋅ = ⇒ PL ( max ) = 25 mW
2 RL 2 ( 2)
PS = VCC ⋅ I CQ = (10 )( 5 ) = 50 mW
So η = 50%

13. 5
I CQ
I BQ = =
= 0.0278 mA
β 180
R1 = RTH = 6 kΩ
VTH = I BQ RTH + VBE ( on ) + (1 + β ) I BQ RE
Set RE = 20 Ω
VTH = ( 0.0278 )( 6 ) + 0.7 + (181)( 0.0278 )( 0.020 )
VTH = 0.967 V
1
VTH = ⋅ RTH ⋅ VCC
R1
1
0.967 = ( 6 )(10 ) ⇒ R1 = 62.0 kΩ
R1
R2 = 6.64 kΩ
8.29
VCC 15
I CQ = = = 15 mA
RL 1
15
I BQ = = 0.15 mA
100
(15)
2
1 V2
PL ( max ) = ⋅ CC = ⇒ PL ( max ) = 112.5 mW
2 RL 2 (1)
Let RTH = 10 kΩ
VTH = I BQ RTH + VBE + (1 + β ) I BQ RE
= ( 0.15 )(10 ) + 0.7 + (101)( 0.15 )( 0.1)
1 1
VTH = 3.715 = ⋅ RTH ⋅ VCC = ⋅ (10 )(15 )
R1 R1
R1 = 40.4 kΩ
R2 = 13.3 kΩ
8.30
⎛ R2 ⎞ ⎛ 1.55 ⎞
VTH = ⎜ ⎟ VCC = ⎜ ⎟ (10 )
⎝ R1 + R2 ⎠ ⎝ 1.55 + 0.73 ⎠
= 6.80 V
RTH = R1 R2 = 0.73 1.55 = 0.496 kΩ
VTH − VBE 6.80 − 0.70
I BQ = =
RTH + (1 + β ) RE 0.496 + ( 26 )( 0.02 )
I BQ = 6.0 mA, I CQ = 150 mA
Av = − g m RL and RL = a 2 RL = ( 3) ( 8 ) = 72 Ω
2
′ ′
I CQ 150
gm = = ⇒ 5.77 A/V
VT 0.026

14. Av = − ( 5.77 )( 72 ) = −415
Vo ′ = Av ⋅ Vi = ( 415 )( 0.017 ) = 7.06 V
7.06
Vo = = 2.35 V
3
7.06
Vo = = 2.35 V
3
7.06
Vo = = 2.35 V
3
PS = I CQ ⋅ VCC = ( 0.15 )(10 ) = 1.5 W
PL 0.345
η= = ⇒ η = 23%
PS 1.5
8.31
a. Assuming the maximum power is being delivered, then
36 9
Vo′ ( peak ) = 36 V ⇒ Vo = = 9 V ⇒ Vrms = ⇒ Vrms = 6.36 V
4 2
36
b. Vo = ⇒ Vo = 25.5 V
2
PL 2
c. Secondary I rms = = ⇒ I rms = 0.314 A
Vrms 6.36
0.314
Primary I P = ⇒ I P = 78.6 mA
4
d.
PS = I CQ .VCC = ( 0.15 )( 36 ) = 5.4 W
2
η= ⇒ η = 37%
5.4
8.32
a.

15. ⎛V ⎞ ⎛1 ⎞
ve = ⎜ π + g mVπ ′
⎟ RE = Vπ ′
⎜ + g m ⎟ RE
⎝ rπ ⎠ ⎝ rπ ⎠
⎛1+ β ⎞
= Vπ ⎜ ′
⎟ RE
⎝ rπ ⎠
vi = Vπ + ve ⇒ Vπ = vi − ve
⎛ 1+ β ⎞
ve = (vi − ve ) ⎜ ′
⎟ RE
⎝ rπ ⎠
1+ β
⋅ RE′
(1 + β ) RE
2
ve rπ ′ v ⎛n ⎞
= = ′
= e where RE = ⎜ 1 ⎟ RL
vi 1 + 1 + β ⋅ R ′ rπ + (1 + β ) RE vi ′ ⎝ n2 ⎠
E
rπ
ve ⎛n ⎞
v0 = so ve − v0 ⎜ 1 ⎟
⎛ n1 ⎞ ⎝ n2 ⎠
⎜ ⎟
⎝ n2 ⎠
v 1 (1 + β ) RE′
so 0 = ⋅
vi ⎛ n1 ⎞ rπ + (1 + β ) RE ′
⎜ ⎟
⎝ n2 ⎠
b.
1 2 n1 I 1
PL = ⋅ I P RL , a = , I CQ = P so PL = .a 2 I CQ RL
2
2 n2 a 2
PS = I CQ .VCC
For η = 50% :
1 2 2
⋅ a I CQ RL a 2 I R
PL VCC VCC V
= 0.5 = 2 = so a 2 = = ⇒ a 2 = CC
CQ L
PS I CQ ⋅ VCC 2VCC I CQ ⋅ RL ( 0.1)( 50 ) 5
c.
r β VT 49 ( 0.026 )
R0 = π = = ⇒ R0 = 0.255 Ω
1 + β (1 + β ) I CQ ( 50 )( 0.1)
8.33
a. With a 10:1 transformer ratio, we need a current gain of 8 through the transistor.
⎛ R1 R2 ⎞ ie ⎛ R1 R2 ⎞
ie = (1 + β ) ib and ib = ⎜ ⎟ ii so we need = 8 = (1 + β ) ⎜ ⎟ where
⎜R R +R ⎟ ii ⎜R R +R ⎟
⎝ 1 2 ib ⎠ ⎝ 1 2 ib ⎠
Rib = rπ + (1 + β ) RL ≈ (1 + β ) RL = (101)( 0.8 ) = 80.8
′ ′

16. ⎛ R1 R2 ⎞
Then 8 = (101) ⎜
⎜ R R + 80.8 ⎟
⎟
⎝ 1 2 ⎠
R1 R2
= 0.0792 or R1 R2 = 6.95 kΩ
R1 R2 + 80.8
2VCC V 12
Set = RL ⇒ I CQ = CC =
′ = 15 mA
2 I CQ ′
RL 0.8
15
I BQ = = 0.15 mA
100
VTH = I BQ RTH + VBE
1
⋅ RTH ⋅ VCC = I BQ RTH + VBE
R1
1
( 6.95)(12 ) = ( 0.15)( 6.95) + 0.7 ⇒ R1 = 47.9 kΩ then R2 = 8.13 kΩ
R1
b.
I
I e = 0.9 I CQ = 13.5 mA = L ⇒ I L = 135 mA
a
1
PL = ( 0.135 ) ( 8 ) ⇒ PL = 72.9 mW
2
2
PS = VCC I CQ = (12 )(15 ) ⇒ PS = 180 mW
PL
η= ⇒ η = 40.5%
PS
8.34
a.
VP = 2 RL PL
VP = 2 ( 8 )( 2 ) = 5.66 V = peak output voltage
VP 5.66
IP = = = 0.708 A = peak output current
RL 8
Set Ve = 0.9VCC = aVP to minimize distortion
( 0.9 )(18)
Then a = ⇒ a = 2.86
5.66
b.
1 ⎛ I P ⎞ 1 ⎛ 0.708 ⎞
Now I CQ = = ⎜ ⎟ ⇒ I CQ = 0.275 A
0.9 ⎜ a ⎟ 0.9 ⎝ 2.86 ⎠
⎝ ⎠
Then PQ = VCC I Q = (18 )( 0.275 ) ⇒ PQ = 4.95 W Power rating of transistor
8.35
a. Need a current gain of 8 through the transistor.

17. ib ⎛ R1 R2 ⎞
= 8 = (1 + β ) ⎜ ⎟ where Rib ≈ (1 + β )( 0.9 ) = 90.9 kΩ
ii ⎜R R +R ⎟
⎝ 1 2 ib ⎠
8 ⎛ R1 R2 ⎞
=⎜ = 0.0792 or R1 R2 = 7.82 kΩ
⎜ R R + 90.9 ⎟
101 ⎝ 1 2 ⎟
⎠
2VCC 12
Set = 0.9 kΩ ⇒ I CQ = = 13.3 mA
2 I CQ 0.9
13.3
I BQ = = 0.133 mA
100
1
Then ( 7.82 )(12 ) = ( 0.133)( 7.82 ) + 0.7 ⇒ R1 = 53.9 kΩ and R 2 = 9.15 kΩ
R1
b.
I
I e = ( 0.9 ) I CQ = 12 mA = L ⇒ I L = 120 mA
a
1
PL = ( 0.12 ) ( 8 ) ⇒ PL = 57.6 mW
2
2
PS = VCC I CQ = (12 )(13.3) ⇒ PS = 159.6 mW
PL 57.6
η= = ⇒ η = 36.1%
PS 159.6
8.36
a. All transistors are matched.
⎛1+ β ⎞ iC
3 mA = iE1 + iB 3 = ⎜ ⎟ iC +
⎝ β ⎠ β
⎛ 61 1 ⎞
3 = ⎜ + ⎟ iC ⇒ iC = 2.90 mA
⎝ 60 60 ⎠
b.
For vo = 6 V , let RL = 200 Ω.
6
io = = 0.03 A = 30 mA ≅ iE 3
200
30
iB 3 = = 0.492 mA
61
iE1 = 3 − 0.492 = 2.508 mA
2.508
iB1 = ⇒ iB1 = 41.11 μ A
61
3
iE 2 ≅ 3 mA ⇒ iB 2 = ⇒ 49.18 μ A
61
iI = iB 2 − iB1 = 49.18 − 41.11 ⇒ iI = 8.07 μ A
Current gain
30 × 10−3
Ai = ⇒ Ai = 3.72 × 103
8.07 × 10−6
⎛i ⎞ ⎛ 30 × 10−3 ⎞
VBE 3 = VT ln ⎜ E 3 ⎟ = ( 0.026 ) ln ⎜ −13 ⎟
⎝ IS ⎠ ⎝ 5 × 10 ⎠
VBE 3 = 0.6453 V
⎛i ⎞ ⎛ 2.508 × 10−3 ⎞
VEB1 = VT ln ⎜ E1 ⎟ = ( 0.026 ) ln ⎜ −13 ⎟
⎝ IS ⎠ ⎝ 5 × 10 ⎠
VEB1 = 0.5807 V

18. vI = v0 + VBE 3 − VEB1 = 6 + 0.6453 − 0.5807
vI = 6.0646 V
Voltage gain
v0 6
Av = = ⇒ Av = 0.989
vI 6.0646
8.37
1
a. For i0 = 1 A, I B 3 ≅ ⇒ 20 mA
50
10 − VEB1 ⎡10 − ( v0,max + VBE 3 ) ⎤
We can then write = 2⎢ − 20 ⎥
R1 ⎢
⎣ R1 ⎥
⎦
10 − VBE 2vo,max
If, for simplicity, we assume VEB1 = VBE 3 = 0.7 V, then = + 40
R1 R1
9.3 2 ( 4 )
If we assume v0,max = 4 V, then = + 40 which yields R1 = R2 = 32.5 Ω
R1 R1
9.3
b. For vI = 0, I E1 = ⇒ I E1 = 0.286 A = I E 2
32.5
Since I S 3,4 = 10 I S1,2 , then I E 3 = I E 4 = 2.86 A
c.
We can write
⎧ rπ 1 ⎫
⎪ rπ 3 + R1 ⎪
1⎪ 1 + β1 ⎪
R0 = ⎨ ⎬
2⎪ 1 + β3 ⎪
⎪ ⎪
⎩ ⎭
βV ( 50 )( 0.026 )
Now rπ 3 = 3 T = = 0.4545 Ω
IC 3 2.86
β1VT (120 )( 0.026 )
rπ 1 = = = 10.91 Ω
I C1 0.286
So
⎧ 10.91 ⎫
0.4545 + 32.5
1⎪⎪ 121 ⎪⎪
R0 = ⎨ ⎬
2⎪ 51 ⎪
⎪
⎩ ⎪
⎭
10.91
32.5 = 32.5 0.0902 = 0.0900
121
1 ⎧ 0.4545 + 0.0900 ⎫
Then R0 = ⎨ ⎬ or R 0 = 0.00534 Ω
2⎩ 51 ⎭
8.38

19. Ri =
1
2
{ ⎣ }
rπ 1 + (1 + β ) ⎡ R1 ( rπ 3 + (1 + β ) 2 RL ) ⎤
⎦
iC1 ≈ 7.2 mA and iC 3 ≈ 7.2 mA
( 60 )( 0.026 )
Then rπ = = 0.217 kΩ
7.2
So Ri =
1
2
{
0.217 + ( 61) ⎡ 2 ( 0.217 + ( 61)( 0.2 ) ) ⎤
⎣ ⎦ }
1
2
{ ⎣ ⎦ }
= 0.217 + 61 ⎡ 2 12.4 ⎤ or Ri = 52.6 kΩ
8.39
a.
b.
V + − VSG
I1 = K1 (VSG + VTP ) =
2
R1
5 = 10 (VSG − 2 ) ⇒ VSG = 2.707 V
2
10 − 2.707
5= ⇒ R1 = R2 = 1.46 kΩ
R1
c. RL = 100 Ω For a sinusoidal output signal:

20. 1 (v ) 1 ( 5)
2 2
PL = ⋅ o = ⋅ ⇒ PL = 125 mW
2 RL 2 0.1
( vo ) ( 5 )
iD 3 ≈ = ⇒ iD 3 = 50 mA
RL 0.1
50
VGS 3 = + 2 = 4.236 V
10
10 − ( 4.236 + 5 )
I1 = ⇒ I D1 = 0.523 mA
1.46
0.523
VSG1 = + 2 = 2.229 V
10
vI = 5 + 4.236 − 2.229 ⇒ vI = 7.007 V
(VI − VGS ) − ( −10 )
= 10 (VGS − 2 )
2
I D2 =
1.46
17.007 − VGS
= 10 (VGS − 4VGS + 4 )
2
1.46
2
14.6VGS − 57.4VGS + 41.4 = 0
( 57.4 ) − 4 (14.6 )( 41.4 )
2
57.4 ±
VGS =
2 (14.6 )
VGS 2 = 2.98 V
I D 2 = 10 ( 2.98 − 2 ) ⇒ I D 2 = 9.60 mA
2
VG 4 = vI − VGS 2 = 7 − 2.98 = 4.02 V
VSG 4 = 5 − 4.02 = 0.98 V ⇒ I D 4 = 0
8.40
For v0 = 0
I Q = I C 3 + I C 2 + I E1
⎛ 1+ βn ⎞ IC 3
I B3 = I E 2 = ⎜ ⎟ IC 2 =
⎝ βn ⎠ βn
I C 3 = (1 + β n ) I C 2
⎛ β ⎞ I
I B 2 = I C 1 = ⎜ P ⎟ I E1 = C 2
⎝ 1+ βP ⎠ βn
⎛ β ⎞
I C 2 = β n ⎜ P ⎟ I E1
⎝ 1+ βP ⎠
⎛ β ⎞
I C 3 = (1 + β n ) β n ⎜ P ⎟ I E1
⎜1+ β ⎟
⎝ p ⎠
⎛ β ⎞ ⎛ β ⎞
I Q = (1 + β n ) β n ⎜ P ⎟ I E1 + β n ⎜ P ⎟ I E1 + I E1
⎝1+ βP ⎠ ⎝ 1+ βP ⎠
⎛ 10 ⎞ ⎛ 10 ⎞
= ( 51)( 50 ) ⎜ ⎟ I E1 + ( 50 ) ⎜ ⎟ I E1 + I E1
⎝ 11 ⎠ ⎝ 11 ⎠
I Q = 2318.18I E1 + 45.45 I E1 + I E1
I E1 = 1.692 μ A ⇒ I C1 = 1.534 μ A
⎛ 10 ⎞
I C 2 = ( 50 ) ⎜ ⎟ (1.692 ) ⇒ I C 2 = 76.9 μ A
⎝ 11 ⎠
⎛ 10 ⎞
I C 3 = ( 51)( 50 ) ⎜ ⎟ (1.692 ) ⇒ I C 3 = 3.92 mA
⎝ 11 ⎠

21. Because of rπ 1 and Z, neglect effect of r0. Then neglecting r01, r02 and r03, we find
VX
I X = g m 3Vπ 3 + g m 2Vπ 2 + g m1Vπ 1 +
rπ 1 + Z
Now
⎛ r ⎞
Vπ 1 = ⎜ π 1 ⎟ VX , Vπ 2 ≅ g m1Vπ 1rπ 2
⎝ rπ 1 + Z ⎠
and
Vπ 3 = ( g m1Vπ 1 + g m 2Vπ 2 ) rπ 3
= ⎡ g m1Vπ 1 + g m 2 ( g m1Vπ 1rπ 2 ) ⎤ rπ 3
⎣ ⎦
⎛ r ⎞
Vπ 3 = ⎜ π 1 ⎟ [ g m1 + g m1 g m 2 rπ 2 ] rπ 3 ⋅ VX
⎝ rπ 1 + Z ⎠
( β + β1 β 2 ) rπ 3
Vπ 3 = 1 ⋅ VX
rπ 1 + Z
⎛ r ⎞ ⎛ βr ⎞
and Vπ 2 = g m1 ⎜ π 1 ⎟ rπ 2VX = ⎜ 1 π 2 ⎟ VX
⎝ rπ 1 + Z ⎠ ⎝ rπ 1 + Z ⎠
( β + β1 β 2 ) β 3 ββ β1 VX
Then I X = 1 ⋅ V X + 1 2 ⋅ VX + ⋅ VX +
rπ 1 + Z rπ 1 + Z rπ 1 + Z rπ 1 + Z
Then
VX rπ 1 + Z
R0 = =
I X 1 + β1 + β1 β 2 + ( β1 + β1 β 2 ) β 3
(10 )( 0.026 )
rπ 1 = = 0.169 MΩ
1.534
Z = 25 kΩ
Then
169 + 25
R0 =
1 + (10 ) + (10 )( 50 ) + ⎡10 + (10 )( 50 ) ⎤ ( 50 )
⎣ ⎦
194
R0 = = 0.00746 kΩ or Ro = 7.46 Ω
26, 011
8.41
a Neglect base currents.
⎛I ⎞
VBB = 2VD = 2VT ln ⎜ Bias ⎟
⎝ IS ⎠
⎛ 5 × 10−3 ⎞
= 2 ( 0.026 ) ln ⎜ −13 ⎟
⇒ VBB = 1.281 V
⎝ 10 ⎠

22. VBE1 + VEB 3 = VBB
I E1 = I E 3 + I C 2
⎛ β ⎞
I B2 = IC 3 = ⎜ P ⎟ I E 3
⎝ 1+ βP ⎠
⎛ β ⎞
IC 2 = β n I B 2 = β n ⎜ P ⎟ I E 3
⎝ 1+ βP ⎠
⎛ β ⎞
I E1 = I E 3 + β n ⎜ P ⎟ IE3
⎝ 1+ βP ⎠
⎡ ⎛ β ⎞⎤
I E1 = I E 3 ⎢1 + β n ⎜ P ⎟⎥
⎣ ⎝ 1+ βP ⎠⎦
⎛ 1+ βn ⎞ ⎛ 1+ βP ⎞ ⎡ ⎛ βP ⎞⎤
⎜ ⎟ I C1 = ⎜ ⎟ I C 3 ⎢1 + β n ⎜ ⎟⎥
⎝ βn ⎠ ⎝ βP ⎠ ⎣ ⎝ 1+ βP ⎠⎦
⎡I ⎤ ⎡I ⎤
VBE1 = VT ln ⎢ C1 ⎥ , VEB 3 = VT ln ⎢ C 3 ⎥
⎣ IS ⎦ ⎣ IS ⎦
⎡ ⎛ 20 ⎞ ⎤
(1.01) I C1 = ⎛
21 ⎞
⎜ ⎟ IC 3 ⎢1 + (100 ) ⎜ 21 ⎟ ⎥
⎝ 20 ⎠ ⎣ ⎝ ⎠⎦
⎡ 21 ⎤
= I C 3 ⎢ + 100 ⎥ = 101.05 I C 3
⎣ 20 ⎦
I C1 = 100.05 I C 3
⎛ 100.05 I C 3 ⎞ ⎛ IC 3 ⎞
VT ln ⎜ ⎟ + VT ln ⎜ ⎟ = VBB
⎝ IS ⎠ ⎝ IS ⎠
⎛ 100.05 I C 3 ⎞
2
VT ln ⎜ 2 ⎟ = VBB
⎝ IS ⎠
2
100.05 I C 3 ⎛V ⎞
2
= exp ⎜ BB ⎟
I S ⎝ VT ⎠
IS ⎛V ⎞
IC 3 = exp ⎜ BB ⎟ = 0.4995 mA = I C3
100.05 ⎝ VT ⎠
Then I E 3 = 0.5245 mA
Now I C1 = 100.05 I C 3 = 49.97 mA = I C1
⎛ 20 ⎞
I C 2 = (100 ) ⎜ ⎟ ( 0.5245 ) = 49.95 mA = I C 2
⎝ 21 ⎠
⎛I ⎞ ⎛ 49.97 × 10−3 ⎞
VBE1 = VT ln ⎜ C1 ⎟ = 0.026 ln ⎜ −13 ⎟
⎝ IS ⎠ ⎝ 10 ⎠
= 0.70037
⎛I ⎞ ⎛ 0.4995 × 10−3 ⎞
VEB 3 = VT ln ⎜ C 3 ⎟ = 0.026 ln ⎜ ⎟
⎝ IS ⎠ ⎝ 10−13 ⎠
= 0.58062
Note: VBE1 + VEB 3 = 0.70037 + 0.58062 = 1.28099
= VBB
b.

23. 10
v0 = 10 V ⇒ iE1 ≈ = 0.10 A = iC1
100
100
iB1 = = 1 mA
100
⎛ 4 × 10−3 ⎞
VBB = 2 ( 0.026 ) ln ⎜ −13 ⎟
= 1.2694 V
⎝ 10 ⎠
⎛ 0.1 ⎞
VBE1 = ( 0.026 ) ln ⎜ −13 ⎟ = 0.7184
⎝ 10 ⎠
VEB 3 = 1.2694 − 0.7184 = 0.55099 V
⎛ 0.55099 ⎞
I C 3 = 10−13 exp ⎜ ⎟ = 0.1598 mA
⎝ 0.026 ⎠
V 2 (10 )
2
PL = 0 = ⇒ PL = 1 W
RL 100
PQ1 = iC1 ⋅ vCE1 = ( 0.1)(12 − 10 ) ⇒ PQ1 = 0.2 W
PQ 3 = iC 3 ⋅ vEC 3 = ( 0.1598 ) (10 − [ 0.7 − 12]) ⇒ PQ 3 = 3.40 mW
iC 2 = (100 )( iC 3 ) = (100 )( 0.1598 ) = 15.98 mA
PQ 2 = iC 2 ⋅ vCE 2 = (15.98 ) (10 − [ −12]) ⇒ PQ 2 = 0.352 W
8.42
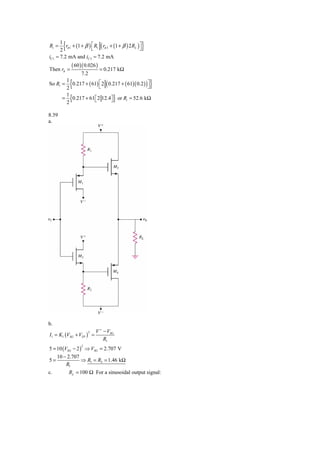
a.
⎛ 10 × 10−3 ⎞
VBB = 3 ( 0.026 ) ln ⎜ −12 ⎟
⇒ VBB = 1.74195 V
⎝ 2 × 10 ⎠
VBE1 + VBE 2 + VEB 3 = VBB
IC 2 IC 2
I C1 ≈ , IC 3 ≈
βn β n2
⎛I ⎞ ⎛I ⎞ ⎛I ⎞
VT ln ⎜ C1 ⎟ + VT ln ⎜ C 2 ⎟ + VT ln ⎜ C 3 ⎟ = VBB
⎝ IS ⎠ ⎝ IS ⎠ ⎝ IS ⎠
⎡ IC ⎤
3
VT ln ⎢ 3 2 3 ⎥ = VBB
⎣ βn IS ⎦
⎛V ⎞
I C 2 = β n I S 3 exp ⎜ BB ⎟
⎝ VT ⎠
⎛ 1.74195 ⎞
= ( 20 ) ( 20 × 10−12 ) 3 exp ⎜ ⎟
⎝ 0.026 ⎠
I C 2 = 0.20 A, I C1 ≈ 10 mA, I C 3 ≈ 0.5 mA
⎛ 10 × 10−3 ⎞
VBE1 = ( 0.026 ) ln ⎜ −12 ⎟
⇒ VBE1 = 0.58065 V
⎝ 2 × 10 ⎠
⎛ 0.2 ⎞
VBE 2 = ( 0.026 ) ln ⎜ −12 ⎟
⇒ VBE 2 = 0.6585 V
⎝ 2 × 10 ⎠
⎛ 0.5 × 10−3 ⎞
VEB 3 = ( 0.026 ) ln ⎜ −12 ⎟
⇒ VEB 3 = 0.50276 V
⎝ 2 × 10 ⎠
b.
1 V2 1 V2
PL = 10 W= ⋅ 0 = ⋅ 0 ⇒ V0 ( max ) = 20 V
2 RL 2 20
For v0 ( max ) :

24. v0 ( 20 )
2 2
PL = = ⇒ PL = 20 W
RL 20
20
i0 ( max ) = − = −1 A
20
iC 5 + iC 4 + iE 3 = −io ( max ) = 1 A
iC 5 ⎛ β n ⎞ iC 4 ⎛ 1 + β p
⎞
iC 5 + ⋅⎜ ⎟+ ⎜ ⎟ =1
βn ⎝ 1 + βn ⎠ βn ⎜ β p
⎝
⎟
⎠
i ⎛ β ⎞ i ⎛ β ⎞ ⎡ 1 ⎛ 1+ β p ⎞⎤
iC 5 + C 5 ⎜ n ⎟ + C 5 ⎜ n ⎟ ⎢ ⎜ ⎟⎥ = 1
βn ⎝ 1 + βn ⎠ βn ⎝ 1 + βn ⎠ ⎣ βn ⎜ β p
⎢ ⎝ ⎟⎥
⎠⎦
⎡ 1 ⎛ 20 ⎞ ⎤ ⎛ 1 ⎞ ⎡ 1 ⎛ 6 ⎞ ⎤
iC 5 ⎢1 + ⎜ ⎟ ⎥ + ⎜ ⎟ ⎢ ⎜ ⎟ ⎥ = 1
⎣ 20 ⎝ 21 ⎠ ⎦ ⎝ 21 ⎠ ⎣ 20 ⎝ 5 ⎠ ⎦
iC 5 (1.05048 ) = 1 iC 5 = 0.952 A
iC 4 = 0.0453 A
iE 3 = 0.00272 A
⎛5⎞
iC 3 = 0.00272 ⎜ ⎟
⎝6⎠
= 0.002267 A
⎛ 2.267 × 10−3 ⎞
VEB 3 = ( 0.026 ) ln ⎜ −12 ⎟ = 0.54206 V
⎝ 2 × 10 ⎠
VBE1 + VBE 2 = 1.74195 − 0.54206 = 1.19989
⎛ I ⎞ ⎛I ⎞
VT ln ⎜ C 2 ⎟ + VT ln ⎜ C 2 ⎟ = 1.19989
⎝ βn IS ⎠ ⎝ IS ⎠
⎛ 1.19989 ⎞
iC 2 = β n ⋅ I S exp ⎜ ⎟
⎝ 0.026 ⎠
= 20 (18.83) mA
iC 2 = 93.9 mA
iC 2 ⎛ β n ⎞ 93.9
iC1 = ⎜ ⎟= = 4.47 mA
β n ⎝ 1 + β n ⎠ 21
PQ 2 = I C 2 ( 24 − ( −20 ) ) = ( 0.0939 ) ( 44 ) = 4.13 W
PQ 5 = ( 0.952 ) ( −10 − ( −24 ) ) = 13.3 W