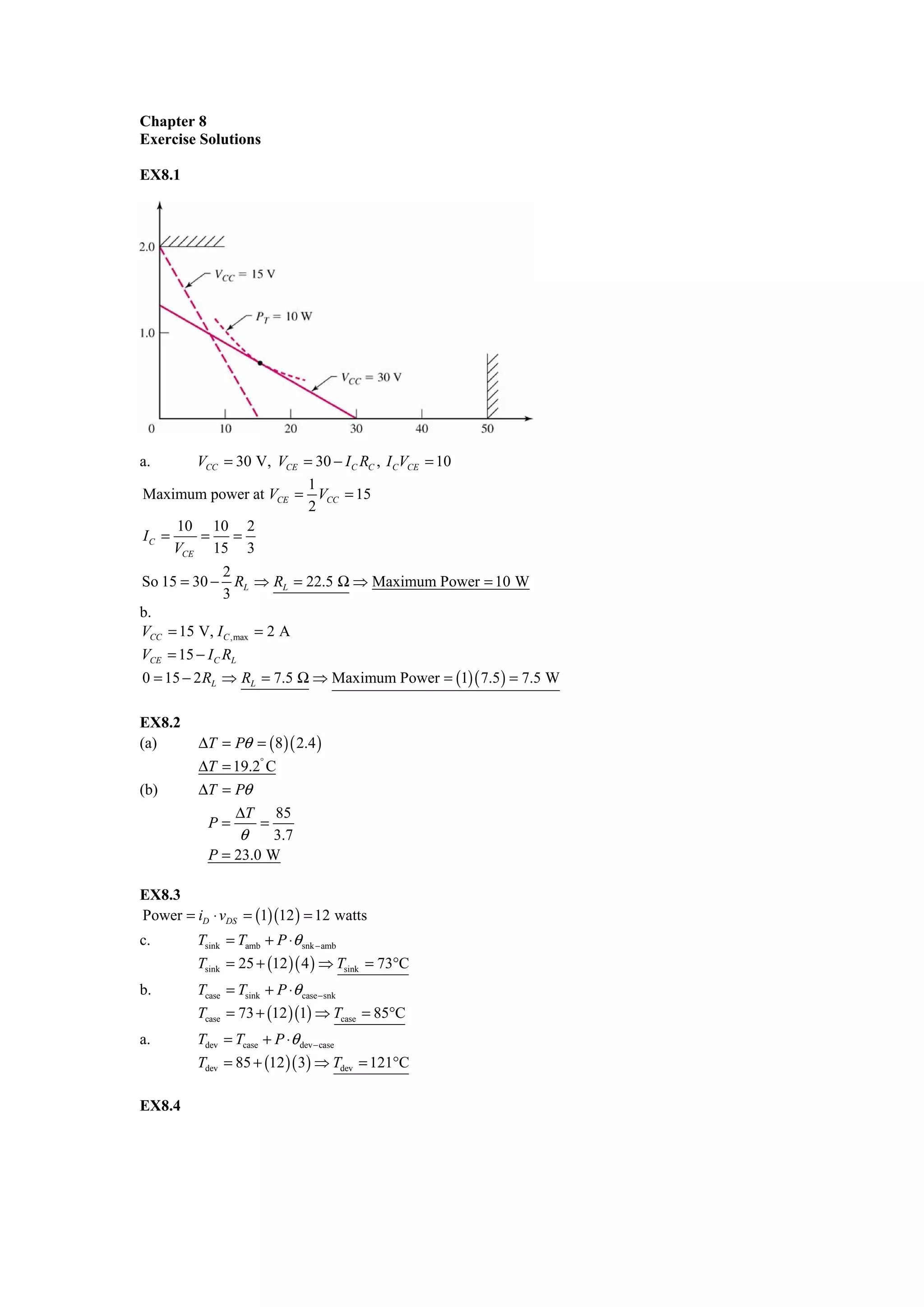
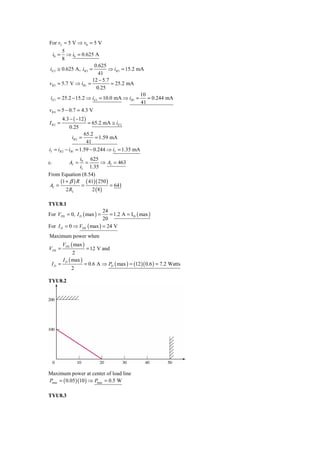
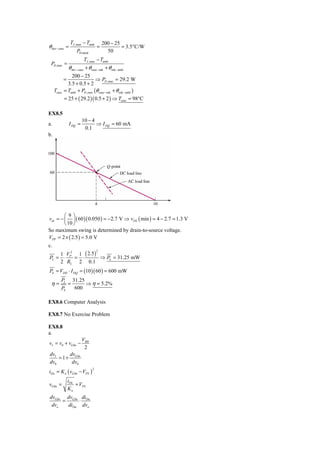
This document contains solutions to exercises from Chapter 8. The summaries are: 1) The first exercise calculates the maximum power transfer for a common emitter amplifier circuit under different voltage supply conditions. 2) The second exercise calculates temperature increases for different components in a circuit based on power dissipation. 3) The third exercise similarly calculates temperature rises for different components based on known power and thermal resistances.

1. Chapter 8
Exercise Solutions
EX8.1
a. VCC = 30 V, VCE = 30 − I C RC , I CVCE = 10
1
Maximum power at VCE = VCC = 15
2
10 10 2
IC = = =
VCE 15 3
2
So 15 = 30 − RL ⇒ RL = 22.5 Ω ⇒ Maximum Power = 10 W
3
b.
VCC = 15 V, I C ,max = 2 A
VCE = 15 − I C RL
0 = 15 − 2 RL ⇒ RL = 7.5 Ω ⇒ Maximum Power = (1)( 7.5 ) = 7.5 W
EX8.2
(a) ΔT = Pθ = ( 8 )( 2.4 )
ΔT = 19.2° C
(b) ΔT = Pθ
ΔT 85
P= =
θ 3.7
P = 23.0 W
EX8.3
Power = iD ⋅ vDS = (1)(12 ) = 12 watts
c. Tsink = Tamb + P ⋅θ snk − amb
Tsink = 25 + (12 )( 4 ) ⇒ Tsink = 73°C
b. Tcase = Tsink + P ⋅θ case − snk
Tcase = 73 + (12 )(1) ⇒ Tcase = 85°C
a. Tdev = Tcase + P ⋅θ dev − case
Tdev = 85 + (12 )( 3) ⇒ Tdev = 121°C
EX8.4

2. TJ ,max − Tamb 200 − 25
θ dev − case = = = 3.5°C/W
PD,rated 50
TJ ,max − Tamb
PD ,max =
θ dev − case + θ case −snk + θ snk − amb
200 − 25
= ⇒ PD ,max = 29.2 W
3.5 + 0.5 + 2
Tcase = Tamb + PD ,max (θ case −snk + θ snk − amb )
= 25 + ( 29.2 )( 0.5 + 2 ) ⇒ Tcase = 98°C
EX8.5
10 − 4
a. I DQ = ⇒ I DQ = 60 mA
0.1
b.
⎛9⎞
vds = − ⎜ ⎟ ( 60 )( 0.050 ) = −2.7 V ⇒ vDS ( min ) = 4 − 2.7 = 1.3 V
⎝ 10 ⎠
So maximum swing is determined by drain-to-source voltage.
VPP = 2 × ( 2.5 ) = 5.0 V
c.
1 VP2 1 ( 2.5 )
2
PL = ⋅ = ⋅ ⇒ PL = 31.25 mW
2 RL 2 0.1
PS = VDD ⋅ I DQ = (10 )( 60 ) = 600 mW
PL 31.25
η= = ⇒ η = 5.2%
PS 600
EX8.6 Computer Analysis
EX8.7 No Exercise Problem
EX8.8
a.
VBB
vI = v0 + vGSn −
2
dvI dv
= 1 + GSn
dv0 dv0
iDn = K n ( vGSn − VTN )
2
iDn
vGSn = + VTN
Kn
dvGSn dvGSn diDn
= ⋅
dvo diDn dvo

3. dvGSn 1 1 1
So = ⋅ ⋅
diDn K n 2 iDn
At v0 = 0, iDn = 0.050 A
dvGSn 1 1 1
So = ⋅ ⋅ =5
diDn 0.2 2 0.050
iDn = iL + iDp
For a small change in v0 → Δ iL = Δ iDn − ( −Δ iDp )
1
So Δ iDn =Δ iL
2
di 1 di 1 1 1 1
or Dn = ⋅ L = ⋅ = ⋅ = 0.025
dv0 2 dv0 2 RL 2 20
dvGSn
Then = ( 5 )( 0.025 ) = 0.125
dv0
dvI dv 1
Then = 1 + 0.125 = 1.125 and Av = 0 = ⇒ Av = 0.889
dv0 dvI 1.125
b. For v0 = 5 V, iL = 0.25 A = iDn , and iDp = 0
dvGSn dvGSn diDn
= ⋅
dv0 diDn dv0
dvGSn 1 1 1 1 1 1
= ⋅ ⋅ = ⋅ ⋅ = 2.24
diDn K n 2 iDn 0.2 2 0.25
diDn diL 1
= = = 0.05
dv0 dv0 20
dvGSn
= ( 2.24 )( 0.05 ) = 0.112
dv0
dvI
= 1 + 0.112 = 1.112
dv0
dv0 1
Av = = ⇒ Av = 0.899
dvI 1.112
EX8.9
a.
Rb = rπ + (1 + β ) RE and RE = a 2 RL = (10 ) ( 8 ) = 800 Ω
2
′ ′
Ri = 1.5 kΩ = RTH Rb
V 18
I Q = 2CC = = 22.5 mA
a RL (10 )2 ( 8 )
(100 )( 0.026 )
rπ = = 0.116 kΩ
22.5
Rb = 0.116 + (101)( 0.8 ) = 80.9 kΩ
RTH ( 80.9 )
1.5 = RTH 80.9 = ⇒ ( 80.9 − 1.5 ) RTH = (1.5 )( 80.9 ) ⇒ RTH = 1.53 kΩ
RTH + ( 80.9 )
⎛ R2 ⎞ 1
VTH = ⎜ ⎟ VCC = ⋅ RTH ⋅ VCC
⎝ R1 + R2 ⎠ R1

4. IQ 22.5
I BQ = = = 0.225 mA
β 100
V − 0.7 1
I BQ = TH ⇒ (1.53)(18 ) = ( 0.225 )(1.53) + 0.7 ⇒ R1 = 26.4 kΩ
RTH R1
26.4 R2
= 1.53
26.4 + R2
( 26.4 − 1.53) R2 = (1.53)( 26.4 ) ⇒ R2 = 1.62 kΩ
b.
vE = 0.9VCC = ( 0.9 )(18 ) = 16.2 V
iE = 0.9 I CQ = ( 0.9 )( 22.5 ) = 20.25 mA
v 16.2
v0 = E = ⇒ VP = 1.62 V
a 10
i0 = aiE = (10 )( 20.25 ) ⇒ I P = 203 mA
1
PL = (1.62 )( 0.203) ⇒ PL = 0.164 W
2
EX8.10
a.
⎛V ⎞ ⎛ IC ⎞
I C = I SQ exp ⎜ BE ⎟ ⇒ VBE = VT ln ⎜⎜ ⎟
⎟
⎝ VT ⎠ ⎝ I SQ ⎠
⎛ 5 × 10−3 ⎞
VBE = ( 0.026 ) ln ⎜ −13 ⎟
= 0.6225 V ⇒ VD1 = VD 2 = 0.6225
⎝ 2 × 10 ⎠
⎛ 0.6225 ⎞
I Bias = I D = I SD exp ⎜ ⎟
⎝ 0.026 ⎠
⎛ 0.6225 ⎞
= 5 × 10−13 exp ⎜ ⎟
⎝ 0.026 ⎠
I Bias = 12.5 mA
2
b. V0 = 2 V, iL = = 26.7 mA
0.075
1st approximation:
iCn ≅ 26.7 mA, iBn = 0.444 mA
⎛ 26.7 × 10−3 ⎞
VBE = ( 0.026 ) ln ⎜ −13 ⎟
= 0.6661
⎝ 2 × 10 ⎠
I D = 12.5 − 0.444 = 12.056 mA
⎛ 12.056 × 10−3 ⎞
VD = ( 0.026 ) ln ⎜ −13 ⎟ = 0.6216
⎝ 5 × 10 ⎠
2VD = 1.243 V
VEB = 2VD − VBE = 0.5769
⎛ 0.5769 ⎞
icP = 2 × 10−13 exp ⎜ ⎟ = 0.866 mA
⎝ 0.026 ⎠
2nd approximation:
iEn = iL + iCP = 26.7 + 0.866 ≅ 27.6 mA = iEn
⎛ 60 ⎞
iCn = ⎜ ⎟ ( 27.6 ) ⇒ iCn = 27.1 mA
⎝ 61 ⎠
iBn = 0.452 mA
I D = 12.5 − 0.452 ⇒ I D = 12.05 mA

5. ⎛ 27.1× 10−3 ⎞
VBEn = ( 0.026 ) ln ⎜ −13 ⎟
⇒ VBEn = 0.6664 V
⎝ 2 × 10 ⎠
⎛ 12.05 × 10−3 ⎞
VD = ( 0.026 ) ln ⎜ −13 ⎟ = 0.6215 V
⎝ 5 × 10 ⎠
2VDD = 1.243 V
VEB = 1.243 − 0.6664 ⇒ VEBp = 0.5766 V
⎛ 0.5766 ⎞
iCP = 2 × 10−13 exp ⎜ ⎟ ⇒ iCP = 0.856 mA
⎝ 0.026 ⎠
c.
10
V0 = 10 V, iL = = 133 mA
0.075
iEn ≅ iL = 133 mA ⇒ iCN = 131 mA
iBn = 2.18 mA ⇒ I D = 12.5 − 2.18 ⇒ I D = 10.3 mA
⎛ 10.3 × 10−3 ⎞
VD = ( 0.026 ) ln ⎜ −13 ⎟
= 0.6175
⎝ 5 × 10 ⎠
2VDD = 1.235 V
⎛ 131× 10−3 ⎞
VBEn = ( 0.026 ) ln ⎜ −13 ⎟
⇒ VBEn = 0.7074 V
⎝ 2 × 10 ⎠
VEBp = 1.235 − 0.7074 ⇒ VEBp = 0.5276 V
⎛ 0.5276 ⎞
iCP = 2 × 10−13 exp ⎜ ⎟ ⇒ iCP = 0.130 mA
⎝ 0.026 ⎠
EX8.11 No Exercise Problem
EX8.12
a.
vI = 0 = v0 , vB 3 = 0.7 V
12 − 0.7 11.3
I R1 = = ⇒ I R1 = 45.2 mA
R1 0.25
If transistors are matched, then
iE1 = iE 3
i
iR1 = iE1 + iB 3 = iE1 + E 3
1+ β
⎛ 1 ⎞ ⎛ 1⎞
iR1 = iE1 ⎜ 1 + ⎟ = iE1 ⎜ 1 + ⎟
⎝ 1+ β ⎠ ⎝ 41 ⎠
45.2
iE1 = ⇒ iE1 = iE 2 = 44.1 mA
1.024
i 44.1
iB1 = iB 2 = E1 = ⇒ iB1 = iB 2 = 1.08 mA
1+ β 41
b.

6. For vI = 5 V ⇒ v0 = 5 V
5
i0 =⇒ i0 = 0.625 A
8
0.625
iE 3 ≅ 0.625 A, iB 3 = ⇒ iB 3 = 15.2 mA
41
12 − 5.7
vB 3 = 5.7 V ⇒ iR1 = = 25.2 mA
0.25
10
iE1 = 25.2 − 15.2 ⇒ iE1 = 10.0 mA ⇒ iB1 = = 0.244 mA
41
vB 4 = 5 − 0.7 = 4.3 V
4.3 − ( −12 )
I R2 = = 65.2 mA ≅ iE 2
0.25
65.2
iB 2 = = 1.59 mA
41
iI = iB 2 − iB1 = 1.59 − 0.244 ⇒ iI = 1.35 mA
i0 625
c. AI =
= ⇒ AI = 463
iI 1.35
From Equation (8.54)
(1 + β ) R ( 41)( 250 )
AI = = = 641
2 RL 2 (8)
TYU8.1
24
For VDS = 0, I D ( max ) = = 1.2 A = I D ( max )
20
For I D = 0 ⇒ VDS ( max ) = 24 V
Maximum power when
VDS ( max )
VDS = = 12 V and
2
I D ( max )
ID = = 0.6 A ⇒ PD ( max ) = (12 )( 0.6 ) = 7.2 Watts
2
TYU8.2
Maximum power at center of load line
Pmax = ( 0.05 )(10 ) ⇒ Pmax = 0.5 W
TYU8.3

7. a. PQ = VCEQ ⋅ I CQ = ( 7.5 )( 7.5 )
PQ = 56.3 mW
1 VP2 1 ( 6.5 )
2
b. PL = ⋅ = ⋅ ⇒ PL = 21.1 mW
2 RL 2 1
PS = (15 )( 7.5 ) ⇒ PS = 113 mW
PL 21.1
η= = ⇒ η = 18.7%
PS 113
PQ = 56.3 − 21.1 = 35.2 mW
TYU8.4
1 VP2 20
a. PL = ⋅ ⇒ VP = 2 RL PL = 2 ( 8 )( 25 ) ⇒ VP = 20 V ⇒ VCC = ⇒ VCC = 25 V
2 RL 0.8
VP 20
b. IP = = ⇒ I P = 2.5 A
RL 8
VCCVP VP2
c. PQ = −
π RL 4 RL
( 25 )( 20 ) ( 20 )
2
PQ = − = 19.9 − 12.5 ⇒ PQ = 7.4 W
π (8) 4 (8)
π VP π 20
d. η= = ⋅ ⇒ η = 62.8%
4VCC 4 25
TYU8.5
( 4)
2
1 VP2
a. PL = ⋅ = ⇒ PL = 80 mW
2 RL 2 ( 0.1)
VP 4
b. IP = = ⇒ I P = 40 mA
RL 0.1
VCCVP VP2
c. PQ = −
π RL 4 RL
( 5 )( 4 ) ( 4 )
2
PQ = − = 63.7 − 40 ⇒ PQ = 23.7 mW
π ( 0.1) 4 ( 0.1)
π VP π 4
d. η= = ⋅ ⇒ η = 62.8%
4VCC 4 5
TYU8.6
a.
1 ⎛ 2V ⎞ VCC 12
I CQ ≅ ⋅ ⎜ CC ⎟= = = 8 mA
2 ⎝ RL ⎠ RL 1.5
RTH = R1 R2
⎛ R2 ⎞ 1
VTH = ⎜ ⎟ VCC = ⋅ RTH ⋅ VCC
⎝ R1 + R2 ⎠ R1
I CQ 8 VTH − VBE
I BQ = = = 0.107 mA =
β 75 RTH + (1 + β ) RE

8. Let RTH = (1 + β ) RE = ( 76 )( 0.1) = 7.6 kΩ
1
⋅ ( 7.6 )(12 ) − 0.7
R1
0.107 =
7.6 + 7.6
1
⋅ ( 91.2 ) = 2.33 ⇒ R1 = 39.1 kΩ
R1
39.1R2
= 7.6 ⇒ ( 39.1 − 7.6 ) R2 = ( 7.6 )( 39.1) ⇒ R2 = 9.43 kΩ
39.1 + R2
b.
1 1
PL = ⋅ ( 0.9 I CQ ) RL = ⎡( 0.9 )( 8 ) ⎤ (1.5 ) ⇒ PL = 38.9 mW
2 2
2 2⎣ ⎦
PS = VCC I CQ = (12 )( 8 ) = 96 mW
PQ = PS − PL = 96 − 38.9 ⇒ PQ = 57.1 mW
PL 38.9
η= = ⇒ η = 40.5%
PS 96
TYU8.7
I E = I E 3 + IC 4 + IC 5
= I E 3 + IC 4 + β5 I B5
= I E 3 + β 4 I B 4 + β 5 (1 + β 4 ) I B 4
I E = (1 + β 3 ) I B 3 + β 4 β 3 I B 3 + β 5 (1 + β 4 ) β 3 I B 3
If β 4 and β 5 are large, then I E ≅ β 3 β 4 β 5 I B 3
So that composite current gain is β ≅ β 3 β 4 β 5