This document contains solutions to exercises from Chapter 7. The exercises involve analyzing RC circuits, operational amplifiers, and transistors. The solutions calculate values like capacitance, frequency response, gain, and bias points by setting up and solving equations that model the circuit behavior. Circuit diagrams are included with some of the solutions. The exercises cover topics like low-pass filters, amplifiers, and basic transistor circuits.

1. Chapter 7
Exercise Solutions
EX7.1
(a)
(i)
RS = RP = 4 kΩ
1 1
ω= =
rS ( RS + RP ) CS
1 1
CS = =
2π f ( RS + RP ) 2π ( 20 )( 4 + 4 ) × 10 3
CS = 0.995 μ F
(ii)
⎛ RP ⎞ ω rS
T ( jω ) = ⎜ ⎟
⎝ RS + RP ⎠ 1 + ω 2 rS2
rS = ( RS + RP ) CS = 7.96 × 10 −3
RP 4
= = 0.5
RS + RP 4 + 4
f = 40 Hz
( 0.5)( 2π )( 40 ) ( 7.96 × 10 −3 )
T ( jω ) =
( )
2
1 + ⎡ 2π ( 40 ) 7.96 × 10 −3 ⎤
⎣ ⎦
T ( jω ) = 0.447
f = 80 Hz
( 0.5)( 2π )(80 ) ( 7.96 × 10 −3 )
T ( jω ) =
( )
2
1 + ⎡ 2π ( 80 ) 7.96 × 10 −3 ⎤
⎣ ⎦
T ( jω ) = 0.485
f = 200 Hz
( 0.5 )( 2π )( 200 ) ( 7.96 × 10 −3 )
T ( jω ) =
( )
2
1 + ⎡ 2π ( 200 ) 7.96 × 10 −3 ⎤
⎣ ⎦
T ( jω ) = 0.498
(b)
1 1
ω= =
rP ( RS RP ) CP
1
CP =
2π f ( RS RP )
1
=
(
2π 500 × 10 3
) (10 10 ) × 10 3
CP = 63.7 pF
EX7.2
a.

2. ⎛ RP ⎞ RP RP
20 log10 ⎜ ⎟ = −1 ⇒ = 0.891 = ⇒ (1 − 0.891) RP = 0.891 ⇒ RP = 8.20 kΩ
⎝ RP + RS ⎠ RP + RS RP + 1
1 1
fL = ⇒ CS =
2π ( RS + RP ) CS 2π (100 )(1 + 8.20 ) × 10 3
CS = 0.173 μ F
1 1
fH = ⇒ CP =
2π ( RS RP ) CP 2π 10( ) (1 || 8.20 ) × 10
6 3
CP = 179 pF
b.
rS = ( RS + RP ) CS
( )(
rS = 1 × 10 3 + 8.20 × 10 3 0.173 × 10 −6 )
rS = 1.59 ms open-circuit time-constant
rP = ( RS RP ) CP
rP = (1 8.20 ) × 10 3 179 × 10 −12( )
rP = 0.160 μ s short-circuit time-constant
EX7.3
a. rS = ( Ri + RS i ) CC
b.
1
f =
2π rS
RTH = R1 R2 = 2.2 20 = 1.98 kΩ
⎛ R2 ⎞ ⎛ 2.2 ⎞
VTH = ⎜ ⎟ VCC = ⎜ ⎟ (10 ) = 0.991 V
⎝ R1 + R2 ⎠ ⎝ 2.2 + 20 ⎠
VTH − VBE ( on ) 0.991 − 0.7
I BQ = = = 0.0132 mA
RTH + (1 + β ) RE 1.98 + ( 201)( 0.1)
I CQ = 2.636 mA
β VT ( 200 )( 0.026 )
rπ = = = 1.97 kΩ
I CQ 2.636
ICQ 2.636
gm = = = 101.4 mA/V
VT 0.026
Rib = τ π + (1 + β ) RE = 1.97 + ( 201)( 0.1) = 22.1 kΩ
RB = R1 R2 = 1.98 kΩ
Ri = RB Rib = 1.98 22.1 = 1.817 kΩ
rS = ( Ri + RSi ) CC
= (1.817 + 0.1) ×10 3 ( )( 47 × 10 )−6
= 90.1 ms
1
f = ⇒ f = 1.77 Hz
(
2π 90.1 × 10 −3 )
Midband Gain

3. − β RC Ri
Aν = ⋅
rπ + (1 + β ) RE Ri + RSi
− ( 200 )( 2 ) 1.82
= ⋅
1.97 + ( 201)( 0.1) 1.82 + 0.1
Aν = −17.2
EX7.4
I DQ = K n (VGS − VTN )
2
a.
0.8
+ 2 = VGS ⇒ VGS = 3.265 V
0.5
VS − ( −5 )
VS = −3.265 ⇒ I DQ =
RS
−3.265 + 5
RS = ⇒ RS = 2.17 kΩ
0.8
5
VD = 0 ⇒ RD = ⇒ RD = 6.25 kΩ
0.8
b.
rS = ( RD + RL ) CC = (10 + 6.25 ) × 10 3 × CC
1 1
f = ⇒ CC =
2π rS (
2π f 16.25 × 10 3 )
1
CC = ⇒ CC = 0.49 μ F
(
2π ( 20 ) 16.25 × 10 3 )
EX7.5
rS = ( RL + Ro ) CC 2
1 1
f = ⇒ CC 2 =
2π rS 2π f ( RL + Ro )
⎧ rπ + ( RS RB ) ⎫
⎪ ⎪
R0 = RE r0 ⎨ ⎬
⎪
⎩ 1+ β ⎪
⎭
From Example 7-5, R0 = 35.5 Ω
1
CC 2 =
2π (10 ) ⎡10 × 10 3 + 35.5⎤
⎣ ⎦
CC 2 = 1.59 μ F
EX7.6
I DQ = K P (VSG + VTP )
2
a.
1
− ( −2 ) = VSG ⇒ VSG = 3.41 V
0.5
VS = 3.41
5 − 3.41
RS = ⇒ RS = 1.59 kΩ
1
5
For VSDG = VSGQ ⇒ VD = 0 ⇒ RD = ⇒ RD = 5 kΩ
1

4. b. rP = ( RD RL ) CL
1 1
f = ⇒ CL =
2π rP 2π f ( RD RL )
1
CL = ⇒ CL = 47.7 pF
( )
2π 10 6 ( 5 10 ) × 10 3
EX7.7
(a)
RTH = 5 K
VTH = −3.7527
−3.7527 − 0.7 − ( −5) 0.54726
I BQ = =
5 + (101)( 0.5) 55.5
= 0.00986
I CQ = 0.986 mA
gm = 37.925 rπ = 2.637 K
5 − Vo Vo
0.986 = − = 1 − Vo ( 0.4 )
5 5
Vo = 0.035
(b)
Rib
RS ϭ 0.1 k⍀
V0
ϩ
Vi ϩ RTH ϭ RC ͉͉RL ϭ
Ϫ V␲ r␲
5 k⍀ gmV␲ 2.5 k⍀
Ϫ
RE ϭ
0.5 k⍀
Vo = − gmVπ ( RC RL )
Rib = rπ + (1 + β ) RE = 2.64 + (101)( 0.5) = 53.14 K
Vb Vb Vb
Vπ = = =
⎛1+ β ⎞ ⎛ 101 ⎞ 14.885
1+ ⎜ ⎟ RE 1 + ⎜ 2.637 ⎟ ( 0.5)
⎝ rπ ⎠ ⎝ ⎠
⎛ RTH Rib ⎞ ⎛ 5 53.14 ⎞
Vb = ⎜ ⎟ Vi = ⎜ ⎟ Vi
⎝ RTH Rib + RS ⎠ ⎝ 5 53.14 + 0.1 ⎠
⎛ 4.57 ⎞
=⎜ ⎟ Vi = 0.9786
⎝ 4.57 + 0.1 ⎠
(37.925)( 2.5)
Av = − ( 0.9786 ) = Av = −6.23
14.885
(c)
EX7.8
a.

5. 0 − 0.7 − ( −10 )
I BQ = = 0.0230 mA
0.5 + (101)( 4 )
I CQ = 2.30 mA
β VT (100 )( 0.026 )
rπ = = = 1.13 kΩ
I CQ 2.30
I CQ 2.30
gm = = = 88.46 mA / V
VT 0.026
RE ( RS + rπ ) CE
rB =
RS + rπ + (1 + β ) RE
=
( 4 × 10 ) ( 0.5 + 1.13) C
3
E
0.5 + 1.13 + (101)( 4 )
1 1
rB = = = 0.7958 ms
2π f B 2π ( 200 )
0.796 × 10 −3
rB = 16.07CE ⇒ CE = ⇒ CE = 49.5 μ F
16.07
b.
rA = RE CE = 4 × 10 3 ( )( 49.5 × 10 ) ⇒ r
−6
A = 0.198 s
1 1
fA = = ⇒ f A = 0.804 H Z
2π rA 2π ( 0.198 )
EX7.9
β 0VT (150 )( 0.026 )
rπ = = = 7.8 kΩ
I CQ 0.5
1
fβ =
2π rπ ( Cπ + Cμ )
1
= ⇒ f β = 8.87 MH Z
(
2π 7.8 × 10 3
) ( 2 + 0.3) × 10 −12
EX7.10
β 0VT (150)(0.026)
rπ = = ⇒ rπ = 3.9 kΩ
I CQ 1
1
fβ =
2π rπ ( Cπ + Cμ )
1
= ⇒ f β = 9.07 MHz
(
2π 3.9 × 10 3
) ( 4 + 0.5) (10 )
−12
fT = β 0 f β = (150 )( 9.07 ) ⇒ fT = 1.36 GHz
EX7.11
RTH = R1 R2 = 200 220 = 104.8 kΩ
⎛ R2 ⎞ ⎛ 220 ⎞
VTH = ⎜ ⎟ VCC = ⎜ ⎟ (5) = 2.619 V
⎝ R1 + R2 ⎠ ⎝ 200 + 220 ⎠
2.62 − 0.7
I BQ = = 0.009316 mA
105 + (101)(1)
I CQ = 0.9316 mA

6. I CQ 0.9316
gm = = ⇒ gm = 35.83 mA/V
VT 0.026
β VT (100)(0.026)
rπ = = ⇒ rπ = 2.79 kΩ
I CQ 0.932
a.
C M = Cμ ⎡1 + gm ( RC RL ) ⎤
⎣ ⎦
C M = ( 2 ) ⎡1 + ( 35.83 )( 2.2 4.7 ) ⎤ ⇒ C M = 109 pF
⎣ ⎦
b.
RB = rS R1 R2 = 100 200 220 = 51.17 kΩ
1
f3 dB =
2π ( RB rπ ) (Cπ + Cμ )
1
= ⇒ f3dB = 0.506 MHz
2π [ 51.17 2.79] × 10 3 × (10 + 109 ) × 10 −12
EX7.12
gm
fT =
2π ( Cgs + Cgd )
gm = 2 K n I DQ
=2 ( 0.2 )( 0.4 )
= 0.5657 mA/V
0.5657 × 10 −3
fT = ⇒ fT = 333 MHz
2π ( 0.25 + 0.02 ) × 10 −12
EX7.13
dc analysis
⎛ R2 ⎞ ⎛ 166 ⎞
VG = ⎜ ⎟ VDD = ⎜
R1 + R2 ⎠ ⎟ (10 ) = 4.15 V
⎝ ⎝ 166 + 234 ⎠
V
I D = S and VS = VG − VGS
RS
VG − VGS
K n (VGS − VTN ) =
2
RS
( 0.5)( 0.5) (VGS − 4VGS + 4 ) = 4.15 − VGS
2
0.25VGS − 3.15 = 0 ⇒ VGS = 3.55 V
2
gm = 2K n (VGS − VTN ) = 2 ( 0.5 )( 3.55 − 2 )
= 1.55 mA/V
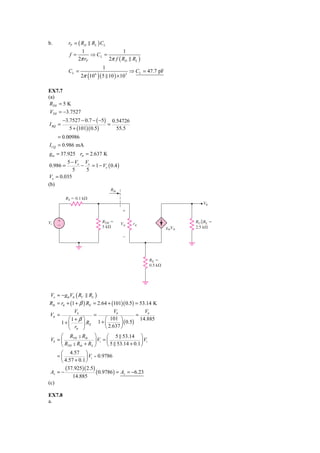
Small-signal equivalent circuit.
Ri ϭ 10 k⍀
V0
ϩ Cgd
Cgs
RG ϭ
Vi ϩ Vgs RD RL
Ϫ R1͉͉R2
gmVgs
Ϫ
a. C M = Cgd (1 + gm ( RD RL ) )
C M = ( 0.1) ⎡1 + (1.55) ( 4 20 )⎤ ⇒ C M = 0.617 pF
⎣ ⎦
b.

7. 1
fH =
2πτ P
τ P = ( RG Ri ) ( Cgs + C M )
RG = R1 R2 = 234 166 = 97.1 kΩ
RG Ri = 97.1 10 = 9.07 kΩ
( )
rP = 9.07 × 10 3 (1 + 0.617 ) × 10 −12 = 14.7 ns
1
fH = ⇒ f H = 10.9 MHz
(
2π 14.7 × 10 −9 )
EX7.14
dc analysis
VTH = 0, RTH = 10 kΩ
0 − 0.7 − ( −5 )
I BQ = = 0.00672 mA
10 + (126 )( 5 )
I CQ = 0.840 mA
β VT (125)( 0.026 )
rπ = = = 3.87 kΩ
I CQ 0.840
I CQ 0.840
gm = = = 32.3 mA/V
VT 0.026
VA 200
r0 = = = 238 kΩ
I CQ 0.84
High-frequency equivalent circuit
C␮
RS ϭ 1 k⍀
V0
ϩ
ϩ RB ϭ
Vi V r␲ r0 RC RL
Ϫ R1͉͉R2 ␲ C␲ gmV␲
Ϫ
a.
Miller Capacitance
C M = Cμ (1 + gm RL )
′
′
RL = r0 RC RL
′
RL = 238 2.3 5 = 1.565 kΩ
C M = ( 3 ) ⎡1 + ( 32.3 )(1.57 ) ⎤ ⇒ Cμ = 155 pF
⎣ ⎦
b.
Req = RS RB rπ = RS R1 R2 rπ
Req = 1 20 20 3.87 = 0.736 kΩ
rP = Re q ( Cπ + C M )
( )
= 0.736 × 10 3 ( 24 + 155 ) × 10 −12
−7
= 1.314 × 10
1
fH = ⇒ f H = 1.21 MHz
(
2π 1.314 × 10 −7 )
c.

8. ⎡ RB τ π ⎤
( Av )M ′
= − gm RL ⎢ ⎥
⎢ RB τ π + RS ⎥
⎣ ⎦
⎡ 10 3.87 ⎤
( Av )M = − ( 32.3 )(1.565 ) ⎢ ⎥ ⇒ ( Av ) M = −37.2
⎣ 10 3.87 + 1 ⎦
EX7.15
The dc analysis
10 − 0.7
I BQ = = 0.00838 mA
100 + (101)(10 )
I CQ = 0.838 mA
β VT (100 )( 0.026 )
rπ = = = 3.10 kΩ
I CQ 0.838
I CQ
gm = = 32.22 mA/V
VT
For the input
⎡⎛ r ⎞ ⎤
rPπ = ⎢⎜ π ⎟ RE RS ⎥ Cπ
⎣⎝ 1 + β ⎠ ⎦
⎡ 3.10 ⎤
=⎢ 10 1⎥ × 10 3 × 24 × 10 −12
⎣ 101 ⎦
= 7.13 × 10 −10 s
1 1
f Hπ = = ⇒ f Hπ = 223 MHz
(
2π rPπ 2π 7.13 × 10 −10 )
For the output
rP μ = [ RC RL ] Cμ = (10 1) × 10 3 × 3 × 10 −12
= 2.73 × 10 −9
1 1
fHμ = = ⇒ f H μ = 58.4 MHz
(
2π rP μ 2π 2.73 × 10 −9 )
⎡ ⎛ rπ ⎞ ⎤
⎢ RE ⎜ ⎟ ⎥
RL ) ⎢ ⎝1+ β ⎠ ⎥
( Aν )M = gm ( RC
⎢ ⎥
⎛ rπ ⎞
⎢ RE ⎜ ⎟ + RS ⎥
⎢
⎣ ⎝1+ β ⎠ ⎥
⎦
⎡ ⎛ 3.1 ⎞ ⎤
⎢ 10 ⎜ 101 ⎟ ⎥
= ( 32.22 )(10 1) ⎢ ⎝ ⎠ ⎥⇒ A
( ν )M = 0.870
⎢ ⎛ 3.1 ⎞ ⎥
⎢ 10 ⎜ 101 ⎟ + 1 ⎥
⎝ ⎠ ⎦
⎣
EX7.16
⎛ R3 ⎞ ⎛ 7.92 ⎞
VB1 = ⎜ ⎟ (12 ) = ⎜ (12 ) = 0.9502 V
⎝ R1 + R2 + R3 ⎠ ⎝ 58.8 + 33.3 + 7.92 ⎟
⎠
Neglecting lose currents
0.9502 − 0.7
IC = = 0.50 mA
0.5
β VT (100 )( 0.026 )
rπ = = = 5.2 K
IC 0.5
IC 0.5
gm = = = 19.23 mA/V
VT 0.026
From Eq (7.127(a)),

9. τ Pπ = [ RS RB1 rπ ][Cπ 1 + C M 1 ]
RB1 = R2 R3 = 33.3 7.92 = 6.398 K
C M 1 = 2Cμ 1 = 6 pF
Then
τ Pπ = [1 6.398 5.2] × 10 × [24 + 6] × 10 ⇒ 22.24 ns
3 −12
1 1
f Hπ = = ⇒ 7.15 MHz
2πτ Pπ 2π ( 22.24 × 10 −9 )
From Eq (7.128(a))
τ P μ = [ RC RL ] C μ 2 = ( 7.5 2 ) × 10 × 3 × 10 ⇒ 4.737 ns
3 −12
1 1
fHμ = = = 33.6 MHz
2πτ Pμ 2π ( 4.737 × 10 −9 )
From Eq. 7.133
⎡ RB1 rπ 1 ⎤
Av = gm 2 ( RC RC ) ⎢ ⎥
⎣ RB1 rπ 1 + RS ⎦
M
⎡ 6.40 5.2 ⎤
= (19.23)( 7.5 2 ) ⎢ ⎥
⎣ 6.40 5.2 + 1 ⎦
⎡ 2.869 ⎤
= (19.23)(1.579 ) ⎢
⎣ 2.869 + 1 ⎥
⎦
Av M
= 22.5
TYU7.1
a.
V0 = − ( gmVπ ) RL
rπ
Vπ = × Vi
1
rπ + + RS
sCC
V0 ( s ) − gm rπ RL
T (s) = =
Vi ( s ) rπ + RS + (1 / sCC )
− gm rπ RL ( sCC )
=
1 + s ( rπ + RS ) CC
gm rπ = β
− β RL ⎛ s ( rπ + RS ) CC ⎞
T (s) = ×⎜ ⎟
rπ + RS ⎜ 1 + s (r + R ) C ⎟
⎝ π S C ⎠
Then τ = ( rπ + RS ) CC
b.
1
f3− dB =
2π ( rπ + RS ) CC
1
f3− dB = ⇒ f3 dB = 53.1 Hz
2π ⎡ 2 × 10 + 1 × 10 3 ⎤ ⎡10 −6 ⎤
⎣
3
⎦⎣ ⎦
rg R ( 2 )( 50 )( 4 )
T ( jω ) max = π m L =
rπ + RS 2 +1
T ( jω ) max = 133
c.

10. ͉T( j␻)͉
133
53.1 Hz f
TYU7.2
a.
⎛ 1 ⎞
V0 = − g mVπ ⎜ RL ⎟
⎝ sCL ⎠
⎛ r ⎞
Vπ = ⎜ π ⎟ × Vi
⎝ rπ + RS ⎠
⎛ 1 ⎞
V0 ( s ) rπ ⎜ RL × sC ⎟
T (s) = = − gm ⎜ L ⎟
Vi ( s ) rπ + RS ⎜ 1 ⎟
⎜ RL + sC ⎟
⎝ L ⎠
− β RL ⎛ 1 ⎞
T (s) = ×⎜ ⎟
rπ + RS ⎝ 1 + sRL CL ⎠
Then τ = RL CL
b.
1 1
f3− dB = = ⇒ f3dB = 3.18 MH Z
( )(
2π RL CL 2π 5 × 10 10 × 10 −12
3
)
gm rπ RL ( 75)(1.5)( 5)
T ( jω ) = =
rπ + RS 1.5 + 0.5
T ( jω ) max = 281
c.
281
͉T( j␻)͉
f 3.18 MHz
TYU7.3
a. Open-circuit time constant ( CL → open )
rS = ( RS + rπ ) CC
( )
= ( 0.25 + 2 ) × 10 3 2 × 10 −6 = 4.5 ms
Short-circuit time constant ( CC → short )
( )(
rP = RL CL = 4 × 10 3 50 × 10 −12 )
rP = 0.2 μ s
b. Midband gain

11. ⎛ rπ ⎞
V0 = − gmVπ RL , Vπ = ⎜ ⎟ Vi
⎝ τ π + RS ⎠
V −g r R
Av = 0 = m π L
Vi rπ + RS
− ( 65 )( 2 )( 4 )
=
2 + 0.25
Av = −231
c.
1 1
fL = = ⇒ f L = 35.4 Hz
(
2π rS 2π 4.5 × 10 −3 )
1 1
fH = = ⇒ f H = 0.796 MHz
(
2π rP 2π 0.2 × 10 −6 )
TYU7.4 Computer Analysis
TYU7.5 Computer Analysis
TYU7.6
βV (100 )( 0.026 )
rπ = 0 T = = 10.4 kΩ
I CQ 0.25
1
fβ =
2π rπ ( Cπ + C μ )
1 1
Cπ + Cμ = =
( )(
2π f β rπ 2π 11.5 × 10 6 10.4 × 10 3 )
Cπ + Cμ = 1.33 pF
Cμ = 0.1 pF ⇒ Cπ = 1.23 pF
TYU7.7
β0
h fe =
1 + j ( f / fβ )
f β = 5 MH Z , β 0 = 100
At f = 50 MH Z
100
h fe = ⇒ h fe = 9.95
2
⎛ 50 ⎞
1+ ⎜ ⎟
⎝ 5 ⎠
⎛ 50 ⎞
Phase = − tan −1 ⎜ ⎟ ⇒ Phase = −84.3°
⎝ 5 ⎠
TYU7.8
f 500
fβ = T = ⇒ f β = 4.17 MHz
β 0 120
1
fβ =
2π rπ (Cπ + C μ )
1 1
Cπ + Cμ = =
2π f β rπ 2π (4.167 × 10 6 )(5 × 10 3 )
Cπ + Cμ = 7.639 pF
Cμ = 0.2 pF ⇒ Cπ = 7.44 pF

12. TYU7.9
(a)
gm = 2K n (VGS − VTN ) = 2 ( 0.4 )( 3 − 1) ⇒ gm = 1.6 mA/V
′
gm = 80% of gm = 1.28 mA/V
gm
′
gm =
1 + gm rS
gm
1 + gm rS =
′
gm
⎛ gm
1 ⎞ 1 ⎛ 1.6 ⎞
rS = ⎜ − 1⎟ = ⎜ − 1⎟
⎝
gm ′
gm ⎠ 1.6 ⎝ 1.28 ⎠
rS = 0.156 kΩ ⇒ rS = 156 ohms
(b)
gm = 2K n (VGS − VTN ) = 2 ( 0.4 )( 5 − 1) ⇒ gm = 3.2 mA/V
gm 3.2
′
gm = = = 2.134
1 + gm rS 1 + ( 3.2 )( 0.156 )
Δgm 3.2 − 2.134
= ⇒ A 33.3% reduction
gm 3.2
TYU7.10
gm
fT =
2π ( CgsT + C gdT )
gm
=
2π ( Cgs + Cgsp + Cgdp )
gm
Cgs = − Cgsp − C gdp
2π fT
0.5 × 10 −3
= − ( 0.01 + 0.01) × 10 −12 ⇒ Cgs = 0.139 pF
(
2π 500 × 10 6
)
TYU7.11
gm
fT =
2π (Cgs + Cgsp + Cgdp )
Cgsp = Cgdp
gm 1× 10−3
2Cgsp = − C gs = − 0.4 × 10−12
2π fT 2π (350 × 106 )
2Cgsp = 0.0547 pF ⇒ Cgsp = Cgdp ≅ 0.0274 pF
TYU7.12
dc analysis
⎛ 50 ⎞
VG = ⎜ ⎟ (10 ) − 5 = −2.5
⎝ 50 + 150 ⎠
VS − ( −5 )
VS = VG − VGS . I D =
RS
VG − VGS + 5
K n (VGS − VTN ) =
2
RS

13. (1)( 2 ) ⎡VGS − 1.6VGS + 0.64 ⎤ = −2.5 − VGS + 5
⎣
2
⎦
2VGS − 2.2VGS − 1.22 = 0
2
( 2.2 ) + 4 ( 2 )(1.22 )
2
2.2 ±
VGS = ⇒ VGS = 1.505 V
2 (2)
gm = 2 K n (VGS − VTN ) = 2 (1)(1.505 − 0.8 )
= 1.41 mA/V
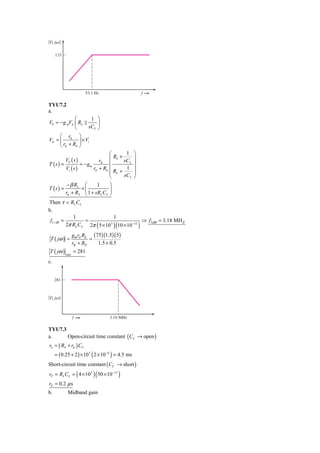
Equivalent circuit
Ri Cgd
V0
ϩ
ϩ RG ϭ
Vi Vgs
Ϫ R1͉͉R2 Cgs
RD
gmVgs
Ϫ
(a) C M = Cgd (1 + gm RD ) = ( 0.2 ) ⎡1 + (1.42 )( 5 ) ⎤ ⇒ C M = 1.61 pF
⎣ ⎦
(b)
τ P = ( Ri RG ) ( Cgs + CM )
rP = [ 20 50 150 ] × 10 3 × ( 2 + 1.61) × 10 −12
( )( )
= 13 × 10 3 3.62 × 10 −12 = 4.71 × 10 −8 s
1 1
fH = = ⇒ f H = 3.38 MHz
(
2π rP 2π 4.71 × 10 −8 )
⎛ RG ⎞
c. ( Av )M = − gm RD ⎜ ⎟
⎝ RG + RS ⎠
⎛ 37.5 ⎞
( Av )M = − (1.41)( 5 ) ⎜ ⎟ ⇒ ( Av ) M = −4.60
⎝ 37.5 + 20 ⎠
TYU7.13 Computer Analysis