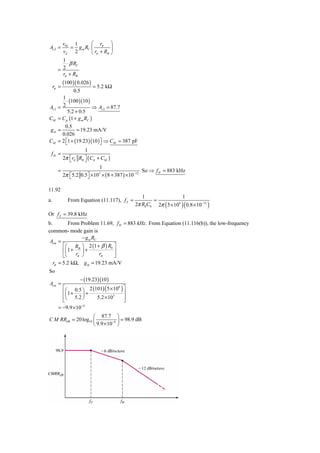
This document contains solutions to problems from Chapter 11. Problem 11.1 solves for resistances in a common emitter amplifier circuit. Part c) finds the maximum and minimum voltages. Problem 11.2 calculates the common-mode gain of a differential amplifier as -0.01012. Problem 11.3a) solves for currents and voltages in a multi-emitter transistor. Part b) solves for currents when the collector voltage is changed.

1. Chapter 11
Problem Solutions
11.1
(a)
−0.7 − ( −3)
= 0.1 ⇒ RE = 23 K
RE
3 − 1.5
= 0.05 ⇒ RC = 30 K
RC
(b) vCE 2 = 6 − iC 2 ( RC + 2 RE ) = 6 − iC 2 ( 76 )
(c) vcm ( max ) ⇒ vCB 2 = 0 ⇒ vCE 2 = 0.7 V
So 0.7 = 6 − iC 2 ( 76 ) ⇒ iC 2 = 69.74 μ A
( v ( max ) − 0.7 ) − ( −3) = 2
CM
( 0.06974 ) ⇒ vCM ( max ) = 0.908 V
23
vCM ( min ) ⇒ VS = −3 V ⇒ vCM ( min ) = −2.3 V
11.2
Ad = 180, C M RRdB = 85 dB
Ad 180
C M RR = 17, 783 = = ⇒ Acm = 0.01012
Acm Acm
Assume the common-mode gain is negative.
v0 = Ad vd + Acm vcm
= 180vd − 0.01012vcm
v0 = 180 ( 2sin ω t ) mV − ( 0.01012 )( 2sin ω t ) V
v0 = 0.36sin ω t − 0.02024sin ω t
Ideal Output: v0 = 0.360sin ω t ( V )
Actual Output: v0 = 0.340sin ω t ( V )
11.3
a.

2. 10 − 2 ( 0.7 )
I1 = ⇒ I1 = 1.01 mA
8.5
I1 1.01
IC 2 = = ⇒ I C 2 ≅ 1.01 mA
2 2
1+ 1+
β (1 + β ) (100 )(101)
⎛ 100 ⎞ ⎛ 1.01 ⎞
IC 4 = ⎜ ⎟⎜ ⎟ ⇒ I C 4 ≅ 0.50 mA
⎝ 101 ⎠ ⎝ 2 ⎠
VCE 2 = ( 0 − 0.7 ) − ( −5 ) ⇒ VCE 2 = 4.3 V
VCE 4 = ⎡5 − ( 0.5 )( 2 ) ⎤ − ( −0.7 ) ⇒ VCE 4 = 4.7 V
⎣ ⎦
b.
For VCE 4 = 2.5 V ⇒ VC 4 = −0.7 + 2.5 = 1.8 V
5 − 1.8
IC 4 = ⇒ I C 4 = 1.6 mA
2
⎛ 1+ β ⎞ ⎛ 101 ⎞
IC 2 + ⎜ ⎟ ( 2IC 4 ) = ⎜ ⎟ ( 2 )(1.6 ) ⇒ I C 2 = 3.23 mA
⎝ β ⎠ ⎝ 100 ⎠
I1 ≈ I C 2 = 3.23 mA
10 − 2 ( 0.7 )
R1 = ⇒ R1 = 2.66 kΩ
3.23
11.4
a. Neglecting base currents
30 − 0.7
I1 = I 3 = 400 μ A ⇒ R1 = ⇒ R1 = 73.25 kΩ
0.4
VCE1 = 10 V ⇒ VC1 = 9.3 V
15 − 9.3
RC = ⇒ RC = 28.5 kΩ
0.2
b.
(100 )( 0.026 )
rπ = = 13 kΩ
0.2
50
r0 ( Q3 ) = = 125 kΩ
0.4
We have
β RC (100 )( 28.5)
Ad = = ⇒ Ad = 62
2 ( rπ + RB ) 2 (13 + 10 )
⎧ ⎫
⎪ ⎪
β RC ⎪ 1 ⎪
Acm = − ⎨ ⎬
rπ + RB ⎪ 2r0 (1 + β ) ⎪
1+
⎪
⎩ rπ + RB ⎪ ⎭
⎧ ⎫
(100 )( 28.5 ) ⎪
⎪ 1 ⎪
⎪
=− ⎨ ⎬ ⇒ Acm = −0.113
13 + 10 ⎪ 2 (125 )(101) ⎪
1+
⎪
⎩ ⎪
13 + 10 ⎭
⎛ 62 ⎞
C M RRdB = 20 log10 ⎜ ⎟ ⇒ C M RRdB = 54.8 dB
⎝ 0.113 ⎠
c.

3. Rid = 2 ( rπ + RB ) = 2 (13 + 10 ) ⇒ Rid = 46 kΩ
1
Ricm = ⎡ rπ + RB + 2 (1 + β ) r0 ⎤
2⎣ ⎦
1
= ⎡13 + 10 + 2 (101)(125 ) ⎤ ⇒ Ricm = 12.6 MΩ
2⎣ ⎦
11.5
IQ ( 0.5)
(a) vCM ( max ) ⇒ VCB = 0 so that vCM ( max ) = 5 − ( RC ) = 5 − (8)
2 2
vCM ( max ) = 3 V
(b)
Vd ⎛ I CQ ⎞ Vd ⎛ 0.25 ⎞ ⎛ 0.018 ⎞
ΔI = g m ⋅ =⎜ ⎟⋅ =⎜ ⎟⎜ ⎟ = 0.08654 mA
2 ⎝ VT ⎠ 2 ⎝ 0.026 ⎠ ⎝ 2 ⎠
ΔVC 2 = ΔI ⋅ RC = ( 0.08654 ) ( 8 ) = 0.692 V
(c)
⎛ 0.25 ⎞ ⎛ 0.010 ⎞
ΔI = ⎜ ⎟⎜ ⎟ = 0.04808 mA
⎝ 0.026 ⎠ ⎝ 2 ⎠
ΔVC 2 = ( 0.04808 )( 8 ) = 0.385 V
11.6
P = ( I1 + I C 4 ) (V + − V − )
I1 ≅ I C 4 so 1.2 = 2 I1 ( 6 ) ⇒ I1 = I C 4 = 0.1 mA
3 − 0.7 − ( −3)
R1 = ⇒ R1 = 53 k Ω
0.1
3 −1
For vCM = +1V ⇒ VC1 = VC 2 = 1 V ⇒ RC = ⇒ RC = 40 k Ω
0.05
One-sided output
1 0.05
Ad = g m RC where g m = = 1.923 mA / V
2 0.026
Then
1
Ad = (1.923)( 40 ) ⇒ Ad = 38.5
2
11.7
a.
IE
0 = 0.7 + ( 2 ) + I E (85) − 5
2
5 − 0.7
IE = ⇒ I E = 0.050 mA
85 + 1
⎛ β ⎞ ⎛ I E ⎞ ⎛ 100 ⎞⎛ 0.050 ⎞
I C1 = I C 2 = ⎜ ⎟⎜ ⎟ = ⎜ ⎟⎜ ⎟
⎝ 1 + β ⎠ ⎝ 2 ⎠ ⎝ 101 ⎠⎝ 2 ⎠
Or I C1 = I C 2 = 0.0248 mA
VCE1 = VCE 2 = ⎡5 − I C1 (100 ) ⎤ − ( −0.7 )
⎣ ⎦
So VCE1 = VCE 2 = 3.22 V
b. vcm ( max ) for VCB = 0 and VC = 5 − I C1 (100 ) = 2.52 V
So vcm ( max ) = 2.52 V
vcm ( min ) for Q1 and Q2 at the edge of cutoff ⇒ vcm ( min ) = −4.3 V
(c) Differential-mode half circuits

4. vd ⎛V ⎞
− ′
= Vπ + ⎜ π + g mVπ ⎟ .RE
2 ⎝ rπ ⎠
⎡ (1 + β ) ⎤
= Vπ ⎢1 + ′
RE ⎥
⎣ rπ ⎦
Then
− ( vd / 2 )
Vπ =
⎡ (1 + β ) ⎤
⎢1 + ′
RE ⎥
⎣ rπ ⎦
1 β RC
vo = − g mVπ RC ⇒ Ad = ⋅
2 rπ + (1 + β ) RE
′
β VT (100 )( 0.026 ) ′
rπ = = = 105 k Ω RE = 2 k Ω
I CQ 0.0248
Then
1 (100 )(100 )
Ad = ⋅ ⇒ Ad = 16.3
2 105 + (101)( 2 )
11.8
a. For v1 = v2 = 0 and neglecting base currents
−0.7 − ( −10 )
RE = ⇒ RE = 62 kΩ
0.15
b.
v02 β RC
Ad = =
vd 2 ( rπ + RB )
β VT (100 )( 0.026 )
rπ = = = 34.7 kΩ
I CQ 0.075
(100 )( 50 )
Ad = ⇒ Ad = 71.0
2 ( 34.7 + 0.5 )
⎡ ⎤
⎢ ⎥
β RC ⎢ 1 ⎥
Acm = −
rπ + RB ⎢ 2 RE (1 + β ) ⎥
⎢1 + ⎥
⎢
⎣ rπ + RB ⎥ ⎦
⎡ ⎤
(100 )( 50 ) ⎢ 1 ⎥
=− ⎢ ⎥ ⇒ Acm = −0.398
34.7 + 0.5 ⎢ 2 ( 62 )(101) ⎥
⎢1 + 34.7 + 0.5 ⎥
⎣ ⎦
71.0
C M RRdB = 20 log10 ⇒ C M RRdB = 45.0 dB
0.398
c.
Rid = 2 ( rπ + RB )
Rid = 2 ( 34.7 + 0.5 ) ⇒ Rid = 70.4 kΩ
Common-mode input resistance
1
Ricm = ⎡ rπ + RB + 2 (1 + β ) RE ⎤
2⎣ ⎦
1
= ⎡34.7 + 0.5 + 2 (101)( 62 ) ⎤ ⇒ Ricm = 6.28 MΩ
2⎣ ⎦
11.9

5. (a)
v1 = v2 = 1 V ⇒ VE = 1.6
9 − 1.6
IE = ⇒ 18.97 μ A
390
IE
= 9.49 μ A I C1 = I C 2 = 9.39 μ A
2
vC1 = vC 2 = ( 9.39 )( 0.51) − 9 = −4.21 V
(b)
9.39
gm = ⇒ 0.361 mA/V
0.026
ΔI = g m d = ( 0.361× 10−3 ) ( 0.005 ) = 1.805 μ A
V
2
ΔvC = (1.805 × 10−6 )( 510 × 103 ) = 0.921 V ⇒ vC 2 = −4.21 + 0.921 ⇒ −3.29 V
vC1 = −4.21 − 0.921 ⇒ −5.13 V
11.10
(a)
v1 = v2 = 0
I E1 = I E 2 ≅ 6 μ A
β = 60
I C1 = I C 2 = 5.90 μ A
vC1 = vC 2 = ( 5.90 )( 0.360 ) − 3
= −0.875 V
VEC1 = VEC 2 = +0.6 − ( −0.875 )
= 1.475 V
(b)
(i)
5.90
gm = ⇒ 0.227 mA/V
0.026
Ad = g m RC = ( 0.227 )( 360 ) = 81.7
Acm = 0
(ii)
g R ( 60 )( 0.026 )
Ad = m C = 40.8 rπ =
2 0.0059
= 264 K
− ( 0.227 )( 360 )
Acm = = −0.0442
2 ( 61)( 4000 )
1+
264
11.11

6. For v1 = v2 = 0.20 V
I C1 = I C 2 = 0.1 mA
vC1 = vC 2 = ( 0.1)( 30 ) − 10
= −7 V
0.1
gm = = 3.846 mA/V
0.026
v
ΔI = g m d = ( 3.846 )( 0.008 ) ⇒ 30.77 μ A
2
ΔvC = ΔI ⋅ RC = ( 30.77 × 10−6 )( 30 × 103 ) = 0.923 V
v2 ↑⇒ I C 2 ↓⇒ vC 2 ↓⇒ vC1 = −7 + 0.923
= −6.077 V
vC 2 = −7 − 0.923
= −7.923 V
11.12
RC = 50 K
For v1 = v2 = 0
−0.7 − ( −10 )
IE =
75
= 0.124 mA
I C1 = I C 2 = 0.0615 mA
0.0615
gm = = 2.365 mA/V
0.026
(120 )( 0.026 )
rπ = = 50.7 K
0.0615
Differential Input
v V
v1 = d v2 = − d
2 2
Half-circuit.
V ⎛ ΔR ⎞
ΔI = + g m d ⇒ ΔvC1 = −ΔI ⎜ RC + ⎟
2 ⎝ 2 ⎠
⎛ ΔR ⎞
ΔvC 2 = +ΔI ⎜ RC − ⎟
⎝ 2 ⎠
⎛ ΔR ⎞ ⎛ ΔR ⎞
vo = ΔvC1 − ΔvC 2 = −ΔI ⎜ RC + ⎟ − ΔI ⎜ RC − ⎟
⎝ 2 ⎠ ⎝ 2 ⎠
= −2ΔIRC
⎛ V ⎞
= −2 ⎜ g m d ⎟ RC
⎝ 2⎠
Ad = − g m RC = − ( 2.365 )( 50 ) = −118.25
Common-mode input.

7. ⎛V ⎞
vcm = Vπ + ⎜ π + g mVπ ⎟ ( 2 RE )
⎝ rπ ⎠
vcm
Vπ =
⎛ β⎞
1 + ⎜ 1 + ⎟ ( 2 RE )
⎝ rπ ⎠
g m vcm β vcm
ΔI = g mVπ = =
⎛1+ β ⎞ rπ + (1 + β )( 2 RE )
1+ ⎜ ⎟ ( 2 RE )
⎝ rπ ⎠
⎛ ΔR ⎞
− β ⎜ RC + ⎟ ⋅ vcm
ΔvC1 = −ΔIR1 = ⎝ 2 ⎠
rπ + (1 + β )( 2 RE )
⎛ ΔR ⎞
− β ⎜ RC − ⎟ vcm
⎝ 2 ⎠
ΔvC 2 = −ΔIR2 =
rπ + (1 + β )( 2 RE )
⎛ ΔR ⎞ ⎛ ΔR ⎞
− β ⎜ RC + ⎟ vcm + β ⎜ RC − ⎟ vcm
vo = ΔvC1 − ΔvC 2 = ⎝ 2 ⎠ ⎝ 2 ⎠
[ ] [ ]
⎛ ΔR ⎞
−2 β ⎜ ⎟ vcm
= ⎝ 2 ⎠
rπ + (1 + β )( 2 RE )
− βΔR − (120 )( 0.5 )
Acm = =
rπ + (1 + β )( 2 RE ) 50.7 + (121)( 2 )( 75 )
= −0.0032966
118.25
C M RR = = 35,870.5
0.0032966
C M R R ∫ = 91.1 dB
dB
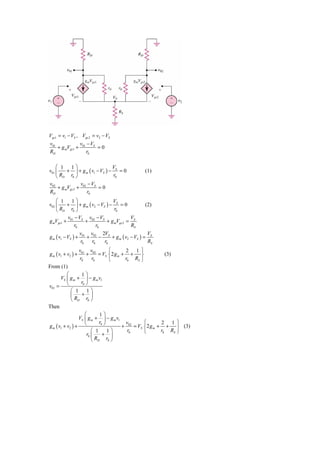
11.13
v1 = v2 = 0
−0.7 − ( −10 )
IE =
75
= 0.124 mA
I C1 = I C 2 = 0.0615 mA
0.0615
gm = = 2.365 mA/V
0.026
Δg m
= 0.01
gm
g m1 = 2.377 mA/V
g m 2 = 2.353 mA/V
(120 )( 0.026 )
rπ = = 50.7 K
0.0615

8. Vd
ΔI = g m
2
V
ΔvC1 = − g m1 d Rc
2
Vd
ΔvC 2 = + gm2 Rc
2
Vd V
vo = ΔvC1 − ΔvC 2 = − g m1 RC − g m 2 d RC
2 2
Vd
=− RC ( g m1 + g m 2 )
2
R −50
Ad = − C ( g m1 + g m 2 ) = ( 2.377 + 2.353) ⇒ Ad = −118.25
2 2
Common-Mode
− g m1 RC vcm − g m 2 RC vcm
ΔvC1 = ΔvC 2 =
⎛ 1+ β ⎞ ⎛ 1+ β ⎞
1+ ⎜ ⎟ ( 2 RE ) 1+ ⎜ ⎟ ( 2 RE )
⎝ rπ ⎠ ⎝ rπ ⎠
vo − ( g m1 − g m 2 ) RC − ( 2.377 − 2.353) ( 50 )
= Acm = =
vcm ⎛ 1+ β ⎞ ⎛ 121 ⎞
1+ ⎜ ⎟ ( 2 RE ) 1+ ⎜ ⎟ ( 2 )( 75 )
⎝ rπ ⎠ ⎝ 50.7 ⎠
−1.2
= ⇒ Acm = −0.003343
358.99
C M R R ∫ = 91 dB
dB
11.14
(a)
v1 = v2 = 0
vE = +0.7 V
5 − 0.7
IE = = 4.3 mA
1
I C1 = I C 2 = 2.132 mA
vC1 = vC 2 = ( 2.132 )(1) − 5
= −2.87 V
(b) v1 = 0.5, v2 = 0 Q2 on
Q1 off
⎛ 120 ⎞
I C1 = 0, I C 2 = 4.3 ⎜ ⎟ mA = 4.264 mA
⎝ 121 ⎠
vC1 = −5 V vC 2 = ( 4.264 ) (1) − 5
vC 2 = −0.736 V
2.132
(c) vE ≈ 0.7 V gm == 82.0 mA/V
0.026
v V (82.0 )
ΔI = g m d ΔvC = ΔI ⋅ RC = g m d ⋅ RC = ⋅ Vd (1) = 41.0Vd
2 2 2
Vd = 0.015 ⇒ Δvc = 0.615 V
vC 2 ↓ vC1 ↑
vC1 = −2.87 + 0.615 = −2.255 V
vC 2 = −2.87 − 0.615 = −3.485 V
11.15

9. (a)
IC 1
gm = = = 38.46 mA/V
VT 0.026
vo 1
Ad = = = 100
vd 0.01
Ad = g m RC
100 = 38.46 RC
Rc = 2.6 K
(b)
With v1 = v2 = 0
vC1 = vC 2 = 10 − (1)( 2.6 ) = 7.4 V ⇒ vcm ( max ) = 7.4 V
11.16
a.
i. ( v01 − v02 ) = 0
ii.
I C1 = I C 2 = 1 mA
v01 − v02 = ⎡V + − I C1 RC1 ⎤ − ⎡V + − I C 2 RC 2 ⎤
⎣ ⎦ ⎣ ⎦
= I C ( RC 2 − RC1 ) = (1)( 7.9 − 8 ) ⇒ v01 − v02 = −0.1 V
b.
⎛v ⎞
I 0 = ( I S 1 + I S 2 ) exp ⎜ BE ⎟
⎝ VT ⎠
⎛v ⎞ 2 × 10−3
So exp ⎜ BE ⎟ = −13 −13
⎝ VT ⎠ 10 + 1.1× 10
= 9.524 × 109
⎛v ⎞
⎟ = (10 )( 9.524 × 10 ) ⇒ I C1 = 0.952 mA
−13 9
I C1 = I S 1 exp ⎜ BE
⎝ VT ⎠
I C 2 = (1.1× 10−13 )( 9.524 × 109 ) ⇒ I C 2 = 1.048 mA
i.
v01 − v02 = I C 2 RC 2 − I C1 RC1 ⇒ v01 − v02 = (1.048 − 0.952 )( 8 ) ⇒ v01 − v02 = 0.768 V
ii.
v01 − v02 = (1.048 )( 7.9 ) − ( 0.952 )( 8 )
v01 − v02 = 8.279 − 7.616 ⇒ v01 − v02 = 0.663 V
11.17
From Equation (11.12(b))
IQ
iC 2 =
1 + evd / VT
1
0.90 =
1 + evd / VT
1
So evd / VT = − 1 = 0.111
0.90
vd = VT ln ( 0.111) = ( 0.026 ) ln ( 0.111) ⇒ vd = −0.0571 V
11.18
From Example 11.2, we have

10. vd ( max ) 1
0.5 + −
4 ( 0.026 ) 1 + e − vd ( max ) / 0.026
= 0.02
v ( max )
0.5 + d
4 ( 0.026 )
⎡ v ( max ) ⎤ 1
0.98 ⎢ 0.5 + d ⎥=
⎢
⎣ 4 ( 0.026 ) ⎥ 1 + e
⎦
− vd ( max ) / 0.026
1
0.490 + 9.423vd ( max ) = − vd ( max ) / 0.026
1+ e
By trial and error
vd ( max ) = 23.7 mV
11.19
a.
For I1 = 1 mA, VBE3 = 0.7 V
20 − 0.7
R1 = ⇒ R1 = 19.3 kΩ
1
V ⎛ I ⎞ 0.026 ⎛ 1 ⎞
R2 = T ⋅ ln ⎜ 1 ⎟ =
⎜I ⎟
⋅ ln ⎜ ⎟ ⇒ R2 = 0.599 kΩ
IQ ⎝ Q⎠ 0.1 ⎝ 0.1 ⎠
b.
(180 )( 0.026 )
rπ 4 = = 46.8 kΩ
0.1
0.1
gm = = 3.846 mA/V
0.026
100
r04 = ⇒ 1 MΩ
0.1
From Chapter 10
R0 = r04 ⎡1 + g m ( RE rπ 4 ) ⎤
⎣ ⎦
RE rπ 4 = 0.599 46.8 = 0.591
R0 = (1) ⎡1 + ( 3.846 )( 0.591) ⎤ = 3.27 MΩ
⎣ ⎦
100
r01 = ⇒ 2 MΩ
0.05
⎡ ⎛ r ⎞⎤
Ricm ≅ ⎡(1 + β ) R0 ⎤ ⎢(1 + β ) ⎜ 01 ⎟⎥
⎣ ⎦
⎣ ⎝ 2 ⎠⎦
= ⎣(181)( 3.27 ) ⎦ ⎣(181)(1) ⎤
⎡ ⎤ ⎡ ⎦
= 592 181 ⇒ Ricm = 139 MΩ
(c) From Eq. (11.32(b))
− g m RC
Acm =
2 (1 + β ) Ro
1+
rπ + RB
0.05
gm = = 1.923 mA / V
0.026
(180 )( 0.026 )
rπ = = 93.6 k Ω
0.05
RB = 0
Then
− (1.923)( 50 )
Acm = ⇒ Acm = −0.00760
2 (181)( 3270 )
1+
93.6

11. 11.19
For vCM = 3.5 V and a maximum peak-to-peak swing in the output voltage of 2 V, we need the
quiescent collector voltage to be
VC = 3.5 + 1 = 4.5 V
Assume the bias is ±10 V , and I Q = 0.5 mA.
Then I C = 0.25 mA
10 − 4.5
Now RC = ⇒ RC = 22 k Ω
0.25
(100 )( 0.026 )
In this case, rπ = = 10.4 k Ω
0.25
Then
(100 )( 22 )
Ad = = 101 So gain specification is met.
2 (10.4 + 0.5 )
For CMRRdB = 80 dB ⇒
1 ⎡ (1 + β ) I Q Ro ⎤ 1 ⎡ (101)( 0.5 ) Ro ⎤
CMRR = 104 = ⎢1 + ⎥ = ⎢1 + ⎥ ⇒ Ro = 1.03 M Ω
2⎣ VT β ⎦ 2 ⎢ ( 0.026 )(100 ) ⎥
⎣ ⎦
Need to use a Modified Widlar current source.
Ro = ro ⎡1 + g m ( RE1 rπ ) ⎤
⎣ ⎦
100
If VA = 100V , then ro = = 200 k Ω
0.5
(100 )( 0.026 )
rπ = = 5.2 k Ω
0.5
0.5
gm = = 19.23 mA / V
0.026
Then 1030 = 200 ⎡1 + (19.23)( RE1 rπ ) ⎤ ⇒ RE1 rπ = 0.216 k Ω = RE1 5.2 ⇒ RE1 = 225 Ω
⎣ ⎦
Also let RE 2 = 225 Ω and I REF ≅ 0.5 mA
11.20
−0.7 − ( −10 )
(a) RE = ⇒ RE = 37.2 k Ω
0.25
(b)

12. Vπ 1 V V ⎛1+ β ⎞ Ve
+ g mVπ 1 + π 2 + g mVπ 2 = e or (1) ⎜ ⎟ (Vπ 1 + Vπ 2 ) =
rπ rπ RE ⎝ rπ ⎠ RE
Vπ 1 V1 − Ve ⎛ r ⎞
= ⇒ Vπ 1 = ⎜ π ⎟ (V1 − Ve )
rπ RB + rπ ⎝ rπ + RB ⎠
Vπ 2 = V2 − Ve
Then
⎛1+ β
⎞ ⎡ rπ ⎤ V
(1) ⎜ ⎟⎢ (V1 − Ve ) + (V2 − Ve )⎥ = e
⎠ ⎣ rπ + RB
⎝ rπ ⎦ RE
From this, we find
rπ + RB
V1 + ⋅ V2
rπ
Ve =
⎡ rπ + RB r + RB ⎤
⎢ +1+ π ⎥
⎣ RE (1 + β ) rπ ⎦
Now
Vo = − g mVπ 2 RC = − g m RC (V2 − Ve )
We have
(120 )( 0.026 ) 0.125
rπ = ≅ 25 k Ω, gm = = 4.81 mA / V
0.125 0.026
(i)
Vd V
Set V1 = and V2 = − d
2 2
Then
⎛ ⎛ 25 + 0.5 ⎞ ⎞
Vd Vd
⎜ 1 − ⎜ 25 ⎟ ⎟
2 ( −0.02 )
⎝ ⎝ ⎠⎠
Ve = = 2
⎡ 25 + 0.5 25 + 0.5 ⎤ 2.026
⎢ +1+ ⎥
⎣ ( 37.2 )(121) 25 ⎦
So
Ve = −0.00494Vd
Now
⎛ V ⎞ V
Vo = − ( 4.81)( 50 ) ⎜ − d − ( −0.00494 )Vd ⎟ ⇒ Ad = o = 119
⎝ 2 ⎠ Vd
(ii)
Set V1 = V2 = Vcm
Then
⎛ 25 + 0.5 ⎞
Vcm ⎜ 1 + ⎟
⎝ 25 ⎠ V ( −2.02 )
Ve = = cm
⎡ 25 + 0.5 25 + 0.5 ⎤ 2.02567
⎢ +1+ ⎥
⎣ ( 37.2 )(121) 25 ⎦
Ve = Vcm ( 0.9972 )
Then
Vo = − ( 4.81)( 50 ) ⎡Vcm − Vcm ( 0.9972 ) ⎤
⎣ ⎦
Vo
or Acm = = −0.673
Vcm
11.21
From Equation (11.18)

13. v0 = vC 2 − vC1 = g m RC vd
I CQ
gm =
VT
For I Q = 2 mA, I CQ = 1 mA
1
Then g m = = 38.46 mA/V
0.026
Now 2 = ( 38.46 ) RC ( 0.015 )
So RC = 3.47 kΩ
Now VC = V + − I C RC = 10 − (1)( 3.47 )
= 6.53 V
For VCB = 0 ⇒ vcm ( max ) = 6.53 V
11.22
The small-signal equivalent circuit is
A KVL equation: v1 = Vπ 1 − Vπ 2 + v2
v1 − v2 = Vπ 1 − Vπ 2
A KCL equation
Vπ 1 V
+ g mVπ 1 + π 2 + g mVπ 2 = 0
rπ rπ
⎛1 ⎞
(Vπ 1 + Vπ 2 ) ⎜ + g m ⎟ = 0 ⇒ Vπ 1 = −Vπ 2
⎝ rπ ⎠
1 1
Then v1 − v2 = 2Vπ 1 ⇒ Vπ 1 = ( v1 − v2 ) and Vπ 2 = − ( v1 − v2 )
2 2
At the v01 node:
v01 v01 − v02
+ + g mVπ 1 = 0
RC RL
⎛ 1 1 ⎞ ⎛ 1 ⎞ 1
v01 ⎜ + ⎟ − v02 ⎜ ⎟ = g m ( v2 − v1 ) (1)
⎝ RC RL ⎠ ⎝ RL ⎠ 2
At the v02 node:
v02 v02 − v01
+ + g mVπ 2 = 0
RC RL
⎛ 1 1 ⎞ ⎛ 1 ⎞ 1
v02 ⎜ + ⎟ − v01 ⎜ ⎟ = g m ( v1 − v2 ) (2)
⎝ RC RL ⎠ ⎝ RL ⎠ 2
From (1):

14. ⎛ R ⎞ 1
v02 = v01 ⎜ 1 + L ⎟ − g m RL ( v2 − v1 )
⎝ RC ⎠ 2
Substituting into (2)
⎛ R ⎞⎛ 1 1 ⎞ 1 ⎛ 1 1 ⎞ ⎛ 1 ⎞ 1
v01 ⎜1 + L ⎟ ⎜ + ⎟ − g m RL ( v2 − v1/ ) ⎜ + ⎟ − v01 ⎜ ⎟ = g m ( v1 − v2 )
⎝ RC ⎠ ⎝ RC RL ⎠ 2 ⎝ RC RL ⎠ ⎝ RL ⎠ 2
⎛ 1 RL 1 ⎞ 1 ⎡ ⎛ RL ⎞⎤
v01 ⎜ + 2 + ⎟ = g m ( v1 − v2 ) ⎢1 − ⎜ + 1⎟ ⎥
⎝ RC RC RC ⎠ 2 ⎣ ⎝ RC ⎠⎦
v01 ⎛ RL ⎞ 1 ⎛ RL ⎞
⎜2+ ⎟ = − gm ⎜ ⎟ ( v1 − v2 )
RC ⎝ RC ⎠ 2 ⎝ RC ⎠
For v1 − v2 = vd
1
− g m RL
v01
Av1 = = 2
vd ⎛ RL ⎞
⎜2+ ⎟
⎝ RC ⎠
1
g m RL
v02
From symmetry: Av 2 = = 2
vd ⎛ RL ⎞
⎜2+ ⎟
⎝ RC ⎠
v02 − v01 g m RL
Then Av = =
vd ⎛ RL ⎞
⎜2+ ⎟
⎝ RC ⎠
11.23
The small-signal equivalent circuit is
KVL equation: v1 = Vπ 1 − Vπ 2 + v2 or v1 − v2 = Vπ 1 − Vπ 2
KCL equation:

15. Vπ 1 V
+ g mVπ 1 + g mVπ 2 + π 2 = 0
rπ rπ
⎛1 ⎞
(Vπ 1 + Vπ 2 ) ⎜ + g m ⎟ = 0 ⇒ Vπ 1 = −Vπ 2
⎝ rπ ⎠
1
Then v1 − v2 = −2Vπ 2 or Vπ 2 = − ( v1 − v2 )
2
Now v0 = − g mVπ 2 ( RC RL )
1
= g m ( RC RL )( v1 − v2 )
2
v0 1
For v1 − v2 ≡ vd ⇒ Ad = = g m ( RC RL )
vd 2
11.23
a.
10 − 7
RD = ⇒ RD = 6 kΩ
0.5
I Q = I D1 + I D 2 ⇒ I Q = 1 mA
b.
10 = I D ( 6 ) + VDS − VGS
ID
and VGS = + VTN
Kn
0.5
For I D = 0.5 mA, VGS = + 2 = 3.12 V
0.4
and VDS = 10.12
Load line is actually nonlinear.
c. Maximum common-mode voltage when M 1 and M 2 reach the transition point, or
VDS ( sat ) = VGS − VTN = 3.12 = 2 = 1.12V
Then
vcm = v02 − vDS ( sat ) + VGS = 7 − 1.12 + 3.12
Or vcm ( max ) = 9 V
Minimum common-mode voltage, voltage across I Q becomes zero.
So vcm ( min ) = −10 + 3.12
⇒ vcm ( min ) = −6.88 V
11.24

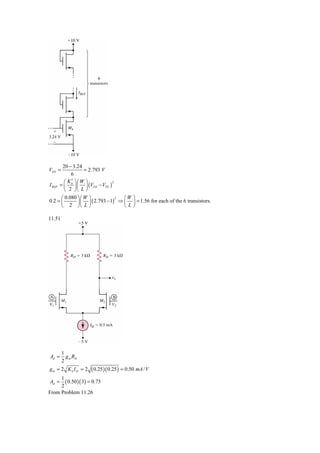
16. We have VC 2 = − g mVπ 2 RC = − g m (Vb 2 − Ve ) RC
and
VC1 = − g mVπ 1 RC = − g m (Vb1 − Ve ) RC
Then
V0 = VC 2 − VC1
= − g m (Vb 2 − Ve ) RC − ⎡ − g m (Vb1 − Ve ) RC ⎤
⎣ ⎦
= g m RC (Vb1 − Vb 2 )
V0
Differential gain Ad = = g m RC
Vb1 − Vb 2
Common-mode gain Acm = 0
11.25
(a)
vcm = 3 V ⇒ VC1 = VC 2 = 3 V
10 − 3
Then RC = ⇒ RC = 70 k Ω
0.1
(b)
CMRRdB = 75 dB ⇒ CMRR = 5623
Now
1 ⎡ (1 + β ) I Q Ro ⎤
CMRR = ⎢1 + ⎥
2⎣ β VT ⎦
1 ⎡ (151)( 0.2 ) Ro ⎤
5623 = ⎢1 + ⎥ ⇒ Ro = 1.45 M Ω
2 ⎢ (150 )( 0.026 ) ⎥
⎣ ⎦
Use a Widlar current source.
Ro = ro [1 + g m RE ]
′
Let VA of current source transistor be 100 V.
100 0.2
Then ro = = 500 k Ω, g m = = 7.69 mA / V
0.2 0.026
(150 )( 0.026 )
rπ = = 19.5 k Ω
0.2
So 1450 = 500 ⎡1 + ( 7.69 ) RE ⎤ ⇒ RE = 0.247 k Ω
⎣ ′⎦ ′
′
Now RE = RE rπ ⇒ 0.247 = RE 19.5 ⇒ RE = 250Ω
⎛I ⎞
Then I Q RE = VT ln ⎜ REF ⎟
⎜ I ⎟
⎝ Q ⎠
⎛ I REF ⎞
( 0.2 )( 0.250 ) = ( 0.026 ) ln ⎜
⎜ ⎟ ⇒ I REF = 1.37 mA
⎟
⎝ ( 0.2 ) ⎠
10 − 0.7 − ( −10 )
Then R1 = ⇒ R1 = 14.1 k Ω
1.37
11.26
At terminal A.
R (1 + δ ) ⋅ R R (1 + δ ) R
RTHA = RA R = = ≅ = 5 kΩ
R (1 + δ ) + R 2+δ 2
Variation in RTH is not significant
⎛ RA ⎞ + R (1 + δ )( 5 ) 5 (1 + δ )
VTHA = ⎜ ⎟V = =
⎝ RA + R ⎠ R (1 + δ ) + R 2+δ

17. At terminal B.
R
RTHB = R R = = 5 kΩ
2
⎛ R ⎞ +
VTHB = ⎜ ⎟ V = 2.5 V
⎝R+R⎠
From Eq. (11.27)
− β RC (V2 − V1 )
VO = where V2 = VTHB and V1 = VTHA
2 ( rπ + RB )
(120 )( 0.026 )
RB = 5 k Ω, rπ = = 12.5 k Ω
0.25
− (120 )( 3)(V2 − V1 )
So VO = = −10.3 (V2 − V1 )
2 (12.5 + 5 )
We can find V2 − V1 = VTHB − VTHA
⎡ 5 (1 + δ ) ⎤
VTHB − VTHA = 2.5 − ⎢ ⎥
⎣ 2+δ ⎦
2.5 ( 2 + δ ) − 5 (1 + δ ) 2.5δ − 5δ
= =
2+δ 2+δ
−2.5δ
≅ = −1.25δ
2
Then VO = − (10.3)( −1.25 ) δ = 12.9δ
So for −0.01 ≤ δ ≤ 0.01
We have −0.129 ≤ VO 2 ≤ 0.129 V
11.27
a.
Rid = 2rπ
(180 )( 0.026 )
rπ = = 23.4 kΩ
0.2
So Rid = 46.8 kΩ
b. Assuming rμ → ∞, then
Ricm ≅ ⎡(1 + β ) R0 ⎤
⎣ ⎦
Ricm = ⎡(181)(1) ⎤
⎣ ⎦
= 181 ⇒ Ricm = 181 MΩ
11.28
(a)
10 − 0.7 − ( −10 )
I1 = = 0.5 ⇒ R1 = 38.6 K
R1
0.026 ⎛ 0.5 ⎞
R2 = ln ⎜ ⎟ ⇒ R2 = 236 Ω
0.14 ⎝ 0.14 ⎠
(b)

18. Ricm ≈ (1 + β ) Ro
0.14
Ro = ro 4 (1 + g m 4 RE ) g m 4 =
′ = 5.385 mA/V
0.026
(180 )( 0.026 )
rπ 4 = = 33.4 K
0.14
′
RE = 33.4 0.236 = 0.234 K
100
ro 4 =
= 714 K
0.14
Ro = 714 ⎡1 + ( 5.385 )( 0.234 ) ⎤
⎣ ⎦
= 1614 K
Ricm = (181)(1614 ) ≈ 292 MΩ
(c)
− g m1 RC 0.07
Acm = g m1 = = 2.692 mA/V
2 (1 + β ) Ro 0.026
1+
rπ 1
(180 )( 0.026 )
rπ 1 = = 66.86 K
0.07
− ( 2.692 )( 40 )
Acm =
2 (181)(1614 )
1+
66.86
Acm = −0.0123
11.29
Ad 1 = g m1 ( R1 rπ 3 )
I Q1 / 2
g m1 = = 19.23I Q1
VT
β VT 2 (100 )( 0.026 ) 5.2
rπ 3 = = =
IQ2 / 2 IQ 2 IQ 2
g m 3 R2 IQ 2 / 2
Ad 2 = , g m3 = = 19.23I Q 2
2 VT
(19.23) I Q 2
Then 30 = ⋅ R2 ⇒ I Q 2 R2 = 3.12 V
2
Maximum vo 2 − vo1 = ±18 mV for linearity
vo3 ( max ) = ( ±18 )( 30 ) mV ⇒ ±0.54 V
so I Q 2 R2 = 3.12 V is OK.
From Ad 1 :

19. ⎛ ⎛ 5.2 ⎞ ⎞
⎜ R1 ⎜
⎜I ⎟ ⎟⎟
⎜ ⎝ Q2 ⎠ ⎟
20 = 19.23I Q1 ( R1 rπ 3 ) = 19.23I Q1 ⎜ ⎟
⎜ R + ⎛ 5.2 ⎞ ⎟
⎜ 1 ⎜ IQ 2 ⎟ ⎟
⎜ ⎟
⎝ ⎝ ⎠⎠
19.23I Q1 R1 ( 5.2 )
20 =
I Q 2 R1 + 5.2
I Q1
Let ⋅ R1 = 5V ⇒ I Q1 R1 = 10 V
2
19.23 (10 )( 5.2 )
Then 20 = ⇒ I Q 2 R1 = 44.8 V
I Q 2 R1 + 5.2
10
Now I Q1 R1 = 10 ⇒ R1 =
I Q1
⎛ 10 ⎞ ⎛ IQ2 ⎞
So I Q 2 ⎜
⎜I ⎟ ⎟ = 44.8 ⇒ ⎜
⎜I ⎟ ⎟
= 4.48
⎝ Q1 ⎠ ⎝ Q1 ⎠
Let I Q1 = 100 μ A, I Q 2 = 448 μ A
Then
I Q 2 R2 = 3.12 ⇒ R2 = 6.96 k Ω
I Q1 R1 = 10 ⇒ R1 = 100 k Ω
11.30
a.
20 − VGS 3
= 0.25 (VGS 3 − 2 )
2
I1 =
50
20 − VGS 3 = 12.5 (VGS 3 − 4VGS 3 + 4 )
2
2
12.5VGS 3 − 49VGS 3 + 30 = 0
( 49 ) − 4 (12.5 )( 30 )
2
49 ±
VGS 3 = ⇒ VGS 3 = 3.16 V
2 (12.5 )
20 − 3.16
I1 = ⇒ I1 = I Q = 0.337 mA
50
IQ
I D1 = ⇒ I D1 = 0.168 mA
2
0.168 = 0.25 (VGS 1 − 2 ) ⇒ VGS1 = 2.82 V
2
VDS 4 = −2.82 − ( −10 ) ⇒ VDS 4 = 7.18 V
VD1 = 10 − ( 0.168 )( 24 ) = 5.97 V
VDS1 = 5.97 − ( −2.82 ) ⇒ VDS 1 = 8.79 V
(b)
(c)

20. Max vCM ⇒ VDS 1 = VDS 2 = VDS ( sat ) = VGS1 − VTN
2.82 − 2 = 0.82 V
Now VD1 = 10 − ( 0.168 )( 24 ) = 5.97 V
VS ( max ) = 5.97 − VDS1 ( sat ) = 5.97 − 0.82
VS ( max ) = 5.15 V
vCM ( max ) = VS ( max ) + VGS1 = 5.15 + 2.82
vCM ( max ) = 7.97 V
vCM ( min ) = V − + VDS 4 ( sat ) + VGS 1
VDS 4 ( sat ) = VGS 4 − VTN = 3.16 − 2 = 1.16 V
Then vCM ( min ) = −10 + 1.16 + 2.82 ⇒ vCM ( min ) = −6.02 V
11.31
a.
I D1 = I D 2 = 120 μ A = 100 ( VGS1 − 1.2 ) ⇒ VGS 1 = VGS 2 = 2.30 V
2
For v1 = v2 = −5.4 V and VDS1 = VDS 2 = 12 V ⇒ −5.4 − 2.30 + 12 = 4.3 V = VD
10 − 4.3
RD = ⇒ RD = 47.5 kΩ
0.12
I Q = I D1 + I D 2 ⇒ I Q = I1 = 240 μ A
I1 = 240 = 200 (VGS 3 − 1.2 ) ⇒ VGS 3 = 2.30 V
2
20 − 2.3
R1 = ⇒ R1 = 73.75 kΩ
0.24
b.
1 1
r04 = = = 416.7 kΩ
λ IQ ( 0.01)( 0.24 )
1 5.4
ΔI Q = ⋅ ΔVDS = ⇒ ΔI Q ≅ 13 μ A
r04 416.7
11.32
(a)
I Q = 160 μ A
k′ ⎛ W ⎞
I D = n ⎜ ⎟ (VGS − VTN )
2
2⎝L⎠
80
80 = ( 4 )(VOS − 0.5 )
2
2
80 = 160 (Vo5 − 0.5 )
2
80
VGS = + 0.5 = 1.207 V
160
5−2
RD = = 37.5 K VDS = 2 − ( −1.207 ) = 3.21 V
0.08
(c)
VDS ( sat ) = VGS − VTN = 1.207 − 0.5 = 0.707 V
Then VS = VO 2 − VDS ( sat ) = 2 − 0.707 = +1.29 V
And v1 = v2 = vcm = VGS + VS = 1.207 + 1.29
vcm = 2.50 V
(b)

21. 11.33
vD = 5 − ( 0.2 )( 8 ) = 3.4 V
ID
VGS = + VTN
Kn
0.2
= + 0.8 = 1.694 V
0.25
VDS ( sat ) = VGS − VTN = 1.694 − 0.8
= 0.894 V
VS = VD − VDS ( sat ) = 3.4 − 0.894
= 2.506
vCM = VS + VGS = 2.506 + 1.694 ⇒ vCM = 4.2 V
(b)
Vd
ΔvD = ΔI D ⋅ RD ΔI D = g m ⋅ gm = 2 Kn I D
2
=2 ( 0.25)( 0.2 ) = 0.4472 mA/V
ΔI D = ( 0.4472 )( 0.05 ) ⇒ 22.36 μ A
ΔvD = ( 22.36 × 10−6 )( 8 × 103 ) = 0.179 V
vD 2 = 3.4 + ΔvD
vD 2 = 3.4 + 0.179 ⇒ vD 2 = 3.58 V
(c)
vd = −50 mV
ΔI D = − ( 0.4472 )( 0.025 ) ⇒ −11.18 μ A
ΔvD = − (11.18 × 10−6 )( 8 × 103 ) = −0.0894 V
vD 2 = 3.4 − 0.0894 ⇒ vD 2 = 3.31 V
11.34
a.
I D1 = I D 2 = 0.5 mA
v01 − v02 = ⎡V + − I D1 RD1 ⎤ − ⎡V + − I D 2 RD 2 ⎤
⎣ ⎦ ⎣ ⎦
v01 − v02 = I D 2 RD 2 − I D1 RD1 = I D ( RD 2 − RD1 )
i. RD1 − RD 2 = 6 kΩ, v01 − v02 = 0
ii. RD1 = 6 kΩ, RD 2 = 5.9 kΩ
v01 − v02 = ( 0.5 )( 5.9 − 6 ) ⇒ v01 − v02 = −0.05 V
b.

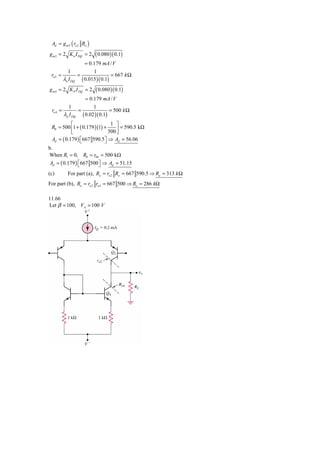
22. K n1 = 0.4 mA / V 2 , K n 2 = 0.44 mA / V 2
VGS1 = VGS 2
I Q = ( K n1 + K n 2 )(VGS − VTN )
2
1 = ( 0.4 + 0.44 )(VGS − VTN ) ⇒ (VGS − VTN ) = 1.19
2 2
I D1 = ( 0.4 )(1.19 ) = 0.476 mA
I D 2 = ( 0.44 )(1.19 ) = 0.524 mA
i.
RD1 = RD 2 = 6 kΩ
v01 − v02 = ( 0.524 − 0.476 )( 6 ) ⇒ v01 − v02 = 0.288 V
ii.
RD1 = 6 kΩ, RD 2 = 5.9 kΩ
v01 − v02 = ( 0.524 )( 5.9 ) − ( 0.476 )( 6 )
= 3.0916 − 2.856 ⇒ v01 − v02 = 0.236 V
11.35
(a) From Equation (11.69)
iD 2 1 Kn ⎛ K ⎞ 2
= − ⋅ vd 1 − ⎜ n ⎟ vd
IQ 2 2IQ ⎜ 2IQ ⎟
⎝ ⎠
0.1 ⎡ 0.1 ⎤ 2
0.90 = 0.50 − ⋅ vd 1 − ⎢ ⎥ vd
2 ( 0.25 ) ⎢ 2 ( 0.25 ) ⎥
⎣ ⎦
+0.40 = − ( 0.4472 ) vd 1 − ( 0.2 ) vd
2
0.8945 = −vd 1 − ( 0.2 ) vd
2
Square both sides
0.80 = vd (1 − [ 0.2] vd )
2 2
( 0.2 ) ( vd2 )
2 2
− vd + 0.80 = 0
2
1 ± 1 − 4 ( 0.2 )( 0.80 )
vd = = 4V 2 or 1V 2
2 ( 0.2 )
Then vd = ± 2 V or ± 1 V
IQ 0.25
But vd max
= = = 1.58
kn 0.1
So vd = ±1V, ⇒ vd = −1V
b. From part (a), vd ,max = 1.58 V
11.36

23. ⎛i ⎞
d ⎜ D1 ⎟
⎜I ⎟ ⎛ K ⎞ 2
⎝ Q⎠= Kn
⋅ 1− ⎜ n
⎜ 2I ⎟ vd + (
⎟ ) vd vd =0
dvd 2IQ ⎝ Q ⎠
Kn
=
2IQ
iD1 1 Kn
So linear = + ⋅ vd
IQ 2 2 IQ
1 Kn ⎡1 Kn ⎛K ⎞ 2 ⎤
+ ⋅ vd ( max ) − ⎢ + ⋅ vd ( max ) ⋅ 1 − ⎜ n ⎟vd ( max ) ⎥
2 2IQ ⎢2 2 IQ ⎝ 2I n ⎠ ⎥
Then ⎣ ⎦ = 0.02
1 Kn
+ ⋅v
2 2 I Q d ( max )
⎡1 Kn ⎤ ⎡1 Kn ⎛K ⎞ 2 ⎤
0.98 ⎢ + ⋅ vd ( max ) ⎥ = ⎢ + ⋅ vd ( max ) ⋅ 1 − ⎜ n ⎟ vd ( max ) ⎥
⎢2 2IQ ⎥ ⎢2 2IQ ⎜ 2I ⎟ ⎥
⎣ ⎦ ⎣ ⎝ Q ⎠ ⎦
0.15 ⎡1 0.15 ⎛ 0.15 ⎞ 2 ⎤
0.49 + 0.98 ⋅ vd ( max ) = ⎢ + ⋅ vd ( max ) ⋅ 1 − ⎜ ⎟ vd ( max ) ⎥
⎜ 2 ( 0.2 ) ⎟
2 ( 0.2 ) ⎢2 2 ( 0.2 ) ⎝ ⎠ ⎥
⎣ ⎦
0.49 + 0.600 vd ( max ) = 0.50 + 0.6124 vd ( max ) ⋅ 1 − ( 0.6124 ) vd ( max )
2
0.600 vd ( max ) = 0.010 + 0.6124 vd ( max ) ⋅ 1 − ( 0.6124 ) vd ( max )
2
By trial and error vd ( max ) ≈ 0.429 V
11.37
(b)
gm = 2 K p I D = 2 ( 0.05 )( 0.008696 )
= 0.0417 mA/V
Vd
ΔI = g m = ( 0.0417 )( 0.05 ) = 0.002085 mA
2
ΔvD = ( 0.002085 )( 510 ) = 1.063
vD 2 ↑⇒ vD 2 = 1.063 − 4.565 = −3.502 V
vD1 = −1.063 − 4.565 = −5.628 V
9 = I S RS + VSG + 1
I S = 2I D
8 = 2 K P RS (VSG + VTP ) + VSG
2
8 = ( 2 )( 0.05 )( 390 )(VSG − 0.8 ) + VSG
2
8 = 39 (VSG − 1.6VSG + 0.64 ) + VSG
2
2
39VSG − 61.4VSG + 16.96 = 0
61.4 ± 3769.96 − 4 ( 39 )(16.96 )
VSG =
2 ( 39 )
= 1.217 V VS = 2.217
I S = 0.01739 mA I D1 = I D 2 ⇒ 8.696 μ A
vD1 = vD 2 = ( 8.696 )( 0.510 ) − 9 = −4.565 V
(b)

24. g m = 2 K P I DQ = 2 ( 0.05 )( 0.008696 ) = 0.0417 mA/V
Vd
ΔvD = ΔI D ⋅ RD = ( 0.0417 )( 0.05 ) = 0.002085 mA
ΔI D = g m ⋅
2
ΔvD = ( 0.002085 )( 510 ) = 1.063 V
v1 ↑, I D1 ↓, vD1 ↓
vD1 = −4.565 − 1.063 = −5.628 V
vD 2 = −4.565 + 1.063 = −3.502 V
11.38
(a)
v1 = v2 = 0
I D = K n (VSG + VTP )
2
ID = 6 μA
6
+ 0.4 = VSG
30
VSG = 0.847 V
VS = +0.847 V
vD = I D RD − 3
= ( 6 )( 0.36 ) − 3 = −0.84 V
VSD = VS − vD = 0.847 − ( −0.84 )
vSD = 1.69 V
(b)
(i)
Ad = g m RD g m = 2 K n I D
=2 ( 30 )( 6 ) = 26.83 μ A/V
Ad = ( 26.83)( 0.36 ) ⇒ Ad = 9.66
Acm = 0
(ii)
g R ( 26.83)( 0.36 )
Ad = m D = ⇒ Ad = 4.83
2 2
− g m RD − ( 26.83)( 0.36 )
Acm = = = −0.0448
1 + 2 g m RO 1 + 2 ( 26.83)( 4 )
11.39

25. For v1 = v2 = −0.30 V
I D1 = I D 2 = 0.1 mA
ID
VSG = − VTP
KP
0.1
= +1 = 2 V
0.1
vD1 = vD 2 = ( 0.1)( 30 ) − 10
= −7 V
gm = 2 K p I D = 2 ( 0.1)( 0.1) = 0.2 mA/V
⎛V ⎞
ΔI D = g m ⎜ d ⎟ = ( 0.2 )( 0.1) = 0.02 mA
⎝ 2⎠
ΔvD = ( ΔI D ) RD = ( 0.02 )( 30 ) = 0.6 V
vD 2 ↑⇒ vD 2 = −7 + 0.6 ⇒ vD 2 = −6.4 V
vD1 = −7 − 0.6 ⇒ vD1 = −7.6 V
11.40
For v1 = v2 = 0
0 = VGS + 2 I D RS − 10
10 = VGS + 2 K n RS (VGS − VTN )
2
= VGS + 2 ( 0.15 )( 75 )(VGS − 1)
2
2
22.5VGS − 44VGS + 12.5 = 0
So VGS = 1.61 V and I D = ( 0.15 )(1.61 − 1) ⇒ 55.9 μ A
2
gm = 2 Kn I D = 2 ( 0.15 )( 0.0559 )
g m = 0.1831 mA/V
Use Half-circuits – Differential gain
⎛V ⎞⎛ ΔR ⎞
vD1 = − g m ⎜ d ⎟ ⎜ RD + ⎟
⎝ 2 ⎠⎝ 2 ⎠
⎛V ⎞⎛ ΔR ⎞
vo 2 = g m ⎜ d ⎟ ⎜ RD − ⎟
⎝ 2 ⎠⎝ 2 ⎠
vo = vD1 − vD 2 = − g mVd RD
v
Ad = o = − g m RD
Vd
Now – Common-Mode Gain

26. Vi = Vgs + g mVgs ( 2 RS ) = Vcm
Vcm
Vgs =
1 + g m ( 2 RS )
⎛ ΔR ⎞
− g m ⎜ RD + D ⎟ Vcm
⎝ 2 ⎠
vD1 =
1 + g m ( 2 RS )
⎛ ΔR ⎞
− gm ⎜ RD − D ⎟ Vcm
⎝ 2 ⎠
vD 2 =
1 + g m ( 2 RS )
vO = vD1 − vD 2
− g m ( ΔRD ) Vcm
So vo =
1 + g m ( 2 RD )
vo − g m ( ΔRD )
Acm = =
Vcm 1 + g m ( 2 RS )
Then
Ad = − ( 0.1831)( 50 ) = −9.16
− ( 0.1831)( 0.5 )
Acm = = −0.003216
1 + ( 0.1831)( 2 )( 75 )
C M R R ∫ = 69.1 dB
bB
11.41
a.
Ad = g m ( r02 r04 )
VA 2 150
r02 = = = 375 kΩ
I C 2 0.4
VA 4 100
r04 = = = 250 kΩ
I C 4 0.4
IC 2 0.4
gm = = = 15.38 mA/V
VT 0.026
Ad = (15.38 ) ( 375 250 ) ⇒ Ad = 2307
b.
RL = r02 r04 = 375 250 ⇒ RL = 150 kΩ
11.41
From 11.40
I D1 = I D 2 = 55.9 μ A
g m = 0.183 mA/V

27. Vd ⎛ +V ⎞
Ad : ΔvD1 = − g m1 ⋅ RD
ΔvD 2 = + g m 2 ⎜ d ⎟ RD
2 ⎝ 2 ⎠
V V
vO = ΔvD1 − ΔvD 2 = − g m1 d RD − g m 2 d RD
2 2
−V −V ⎛ Δg ⎛ Δg ⎞ ⎞
vO = d ⋅ RD ( g m 2 + g m1 ) = d ⋅ RD ⎜ g m − m + ⎜ g m − m ⎟ ⎟
2 2 ⎝ 2 ⎝ 2 ⎠⎠
Ad = − g m RD = − ( 0.183) ( 50 ) = −9.15
⎛ Δg ⎞ ⎛ Δg ⎞
− ⎜ g m + M ⎟ RD vcm ⎜ g m − M ⎟ RD vCM
⎝ 2 ⎠ ⎝ 2 ⎠
ACM : vO = ΔvD1 − ΔvD 2 = +
1 + g m ( 2 RS ) 1 + g m ( 2 RS )
vO −Δg m RD
Acm = = Δg m = ( 0.01) ( 0.183) = 0.00183
vcm 1 + g m ( 2 RS )
− ( 0.00183) ( 50 )
Acm = = −0.003216
1 + ( 0.183)( 2 ) ( 75 )
C M R R ∫ = 69.1 dB
dB
11.42
(a)
v1 = v2 = 0
5 = 2 I D RS + VSG
5 = 2 K p RS (VSG + VTP ) + VSG
2
5 = 2 ( 0.5 )( 2 ) (VSG − 1.6VSG + 0.64 ) + VSG
2
2
5 = 2VSG − 2.2VSG + 1.28
2
2VSG − 2.2VSG − 3.72 = 0
2.2 ± 4.84 + 4 ( 2 )( 3.72 )
VSG =
2 ( 2)
VSG = 2.02 V
5 − 2.02
vS = 2.02 V, IS = = 1.49 mA
2
I D1 = I D 2 = 0.745 mA
vD1 = vD 2 = ( 0.745 (1) − 5 ) ⇒ vD1 = vD 2 = −4.26 V
(b)
5 = I S RS + VSG 2
5 = ( I D1 + I D 2 ) RS + VSG 2
5 = ⎡ K p (VSG1 + VTP ) + K p (VSG 2 + VTP ) ⎤ RS + VSG 2
2 2
⎣ ⎦
VSG1 = VSG 2 − 1
5 = ( 0.5 )( 2 ) ⎡(VSG 2 − 1.8 ) + (VSG 2 − 0.8 ) ⎤ + VSG 2
2 2
⎣ ⎦
5 = ⎡VSG 2 − 3.6VSG 2 + 3.24 + VSG 2 − 1.6VSG 2 + 0.64 ⎤ + VSG 2
⎣
2 2
⎦
2
5 = 2VSG 2 − 4.2VSG 2 + 3.88
2
2VSG 2 − 4.2VSG 2 − 1.12 = 0
4.2 ± 17.64 + 4 ( 2 ) (1.12 )
VSG 2 =
2 ( 2)

28. VSG 2 = 2.339 V VSG1 = 1.339 V
vS = 2.339 V
= 0.5 (1.339 − 0.8 ) = 0.5 ( 2.339 − 0.8 )
2 2
I D1 I D2
I D1 = 0.1453 mA I D2 = 1.184 mA
vD1 = ( 0.1453)(1) − 5 vD 2 = (1.184 ) (1) − 5
vD1 = −4.855 V vD 2 = −3.816 V
(c)
Vd
ΔI = g m gm = 2 K p I D
2
vS ≈ 2.02 V = 2 ( 0.5 )( 0.745 )
g m = 1.22 mA/V
ΔI = (1.22 )( 0.1) = 0.122 mA
ΔvD = ( ΔI ) RD = ( 0.122 )(1) = 0.122 V
vD 2 ↓ vD1 ↑
vD1 = −4.26 + 0.122 vD 2 = −4.26 − 0.122
vD1 = −4.138 V vD 2 = −4.382 V
11.43
IQ
a. gf = ⇒ I Q = g f ( 4VT ) = ( 8 )( 4 )( 0.026 )
4VT
⇒ I Q = 0.832 mA
Neglecting base currents.
30 − 0.7
R1 = ⇒ R1 = 35.2 kΩ
0.832
V 100
b. r04 = r02 = A = = 240 kΩ
I CQ 0.416

29. I CQ 0.416
gm = = = 16 mA / V
VT 0.026
Ad = g m ( r02 || r04 ) = 16 ( 240 || 240 )
⇒ Ad = 1920
(180 )( 0.026 )
Rid = 2rπ , rπ = = 11.25 kΩ
0.416
⇒ Rid = 22.5 kΩ
R0 = r02 || r04 ⇒ R0 = 120 kΩ
c. Max. common-mode voltage when
VCB = 0 for Q1 and Q2 .
Therefore
vcm ( max ) = V + − VEB ( Q3 ) = 15 − 0.7
vcm ( max ) = 14.3 V
Min. common-mode voltage when
VCB = 0 for Q5 .
Therefore
vcm ( min ) = 0.7 + 0.7 + ( −15 ) = −13.6 V
So −13.6 ≤ vcm ≤ 14.3 V
1
Ricm ≅ (1 + β )( 2 R0 )
2
V 100
R0 = A = = 120 kΩ
I Q 0.832
Ricm = (181)(120 ) ⇒ Ricm = 21.7 MΩ
11.43
(a)
gm = 2 Kn I D
=2 ( 0.4 )(1)
g m = 1.265 mA/V
v 1
Ad = o = = 10
vd 0.1
Ad = g m RD
10 = (1.265 ) RD
RD = 7.91 K
(b)
Quiescent v1 = v2 = 0
vD1 = vD 2 = 10 − (1)( 7.91) = 2.09 V
ID 1
VGS = + VTN = + 0.8 = 2.38 V
Kn 0.4
VDS ( sat ) = 2.38 − 0.8 = 1.58
So vcm = vD − VDS ( sat ) + VGS
= 2.09 − 1.58 + 2.38
vcm = 2.89 V
11.44

30. g m RD
Ad =
2
For vCM = 2.5 V
IQ
I D1 = I D 2 = = 0.25 mA
2
10 − 3
Let VD1 = VD 2 = 3 V , then RD = ⇒ RD = 28 k Ω
0.25
g m ( 28 )
Then 100 = ⇒ g m = 7.14 mA / V
2
k′ ⎛ W ⎞
And g m = 2 n ⎜ ⎟ ID
2⎝L ⎠
⎛ 0.080 ⎞ ⎛ W ⎞
7.14 = 2 ⎜ ⎟ ⎜ ⎟ ( 0.25 ) ⇒
⎝ 2 ⎠⎝ L ⎠
⎛W ⎞ ⎛W ⎞
⎜ ⎟ = ⎜ ⎟ = 1274 (Extremely large transistors to meet the gain requirement.)
⎝ L ⎠1 ⎝ L ⎠ 2
Need ACM = 0.10
From Eq. (11.64(b))
g m RD
ACM =
1 + 2 g m Ro
( 7.14 )( 28)
So 0.10 = ⇒ Ro = 140 k Ω
1 + 2 ( 7.14 ) Ro
For the basic 2-transistor current source
1 1
Ro = ro = = = 200 k Ω
λ I Q ( 0.01)( 0.5 )
This current source is adequate to meet common-mode gain requirement.
11.45
Not in detail, Approximation looks good.
a.
−V − ( −5 )
and I S = 2 I D = 2 K n (VGS 1 − VTN )
2
I S = GS 1
RS
5 − VGS 1
= 2 ( 0.050 )(VGS 1 − 1)
2
20
5 − VGS 1 = 2 (VGS1 − 2VGS1 + 1)
2
2
2VGS1 − 3VGS 1 − 3 = 0
( 3) + 4 ( 2 )( 3)
2
3±
VGS1 = ⇒ VGS1 = 2.186 V
2 ( 2)
5 − 2.186
IS = ⇒ I S = 0.141 mA
20
I
I D1 = I D 2 = S ⇒ I D1 = I D 2 = 0.0704 mA
2
v02 = 5 − ( 0.0704 )( 25 ) ⇒ v02 = 3.24 V
b.
g m = 2 K n (VGS − VTN ) = 2 ( 0.05 )( 2.186 − 1)
g m = 0.119 mA/V
1 1
r0 = = = 710 kΩ
λ I DQ ( 0.02 )( 0.0704 )

31. Vgs1 = v1 − VS , Vgs 2 = v2 − VS
v01 v −V
+ g mVgs1 + 01 S = 0
RD r0
⎛ 1 1⎞ V
v01 ⎜ + ⎟ + g m ( v1 − VS ) − S = 0 (1)
⎝ RD r0 ⎠ r0
v02 v − VS
+ g mVgs 2 + 02 =0
RD r0
⎛ 1 1⎞ V
v02 ⎜ + ⎟ + g m ( v2 − VS ) − S = 0 (2)
⎝ RD r0 ⎠ r0
v − V v − VS V
g mVgs1 + 01 S + 02 + g mVgs 2 = S
r0 r0 RS
v01 v02 2VS V
g m ( v1 − VS ) + + − + g m ( v2 − VS ) = S
r0 r0 r0 RS
v01 v02 ⎧ 2 1 ⎫
g m ( v1 + v2 ) + + = VS ⎨2 g m + + ⎬ (3)
r0 r0 ⎩ r0 RS ⎭
From (1)
⎛ 1⎞
VS ⎜ g m + ⎟ − g m v1
v01 = ⎝
r0 ⎠
⎛ 1 1⎞
⎜ + ⎟
⎝ RD r0 ⎠
Then
⎛ 1⎞
VS ⎜ g m + ⎟ − g m v1
⎧ 2 1 ⎫
g m ( v1 + v2 ) + ⎝
r0 ⎠ v
+ 02 = VS ⎨2 g m + + ⎬ (3)
⎛ 1 1⎞ r0 ⎩ r0 RS ⎭
r0 ⎜ + ⎟
⎝ RD r0 ⎠

32. ⎛ 1 1⎞ ⎛ 1⎞ ⎛ 1 1⎞ ⎧ 2 1 ⎫ ⎛ 1 1⎞
g m ( v1 + v2 ) r0 ⎜ + ⎟ + VS ⎜ g m + ⎟ − g m v1 + v02 ⎜ + ⎟ = VS ⎨2 g m + + ⎬ ⋅ r0 ⎜ + ⎟
⎝ RD r0 ⎠ ⎝ r0 ⎠ ⎝ RD r0 ⎠ ⎩ r0 RS ⎭ ⎝ RD r0 ⎠
⎛ r ⎞ ⎛ 1 1⎞ ⎧
⎪⎛ 2 1 ⎞⎛ r0 ⎞ ⎛ 1 ⎞⎪ ⎫
g m ( v1 + v2 ) ⎜ 1 + 0 ⎟ − g m v1 + v02 ⎜ + ⎟ = VS ⎨⎜ 2 g m + + ⎟ ⎜1 + ⎟ − ⎜ gm + ⎟⎬
⎝ RD ⎠ ⎝ RD r0 ⎠ ⎪⎝
⎩ r0 RS ⎠ ⎝ RD ⎠ ⎝ r0 ⎠ ⎪
⎭
⎛ r r ⎞ ⎛ 1 1⎞ ⎧ 2 1 r 2 r 1⎫
g m ⎜ v1 ⋅ 0 + v2 + v2 ⋅ 0 ⎟ + v02 ⎜ + ⎟ = VS ⎨2 g m + + + 2gm ⋅ 0 + + 0 − gm − ⎬
⎝ RD RD ⎠ ⎝ RD r0 ⎠ ⎩ r0 RS RD RD RS RD r0 ⎭
⎛ r ⎞ ⎛ 1 1⎞ ⎧
⎪ 1 1 ⎛ r0 ⎞ 2 ⎫
(1 + g m r0 )⎪ (4)
r
g m ⎜ v1 ⋅ 0 + v2 + v2 ⋅ 0 ⎟ + v02 ⎜ + ⎟ = VS ⎨2 g m + + ⎜1 + ⎟+ ⎬
⎝ RD RD ⎠ ⎝ RD r0 ⎠ ⎪
⎩ r0 RS ⎝ RD ⎠ RD ⎪
⎭
⎛ 1 1⎞ ⎛ 1⎞
Then substituting into (2), v02 ⎜ + ⎟ + g m v2 = VS ⎜ g m + ⎟
⎝ RD r0 ⎠ ⎝ r0 ⎠
⎡ 710 710 ⎤ ⎡1 1 ⎤
Substitute numbers: ( 0.119 ) ⎢ v1 + v2 + v2 ⎥ + v02 ⎢ 25 + 710 ⎥ (4)
⎣ 25 25 ⎦ ⎣ ⎦
⎧ 1 1 ⎛ 710 ⎞ 2 ⎫
= VS ⎨0.119 + + ⎜1 + ⎟ + ⎡1 + ( 0.119 )( 710 ) ⎤ ⎬
⎣ ⎦
⎩ 710 20 ⎝ 25 ⎠ 25 ⎭
( 0.119 ) [ 28.4v1 + 29.4v2 ] + ( 0.0414 ) v02 = VS {0.1204 + 1.470 + 6.8392}
= VS ( 8.4296 )
or VS = 0.4010v1 + 0.4150v2 + 0.00491v02
⎛ 1 1 ⎞ ⎛ 1 ⎞
Then v02 ⎜ + ⎟ + ( 0.119 ) v2 = VS ⎜ 0.119 + ⎟ (2)
⎝ 25 710 ⎠ ⎝ 710 ⎠
v02 ( 0.0414 ) + v2 ( 0.119 ) = ( 0.1204 ) [ 0.401v1 + 0.4150v2 + 0.00491v02 ]
v02 ( 0.0408 ) = ( 0.04828 ) v1 − ( 0.0690 ) v2
v02 = (1.183) v1 − (1.691) v2
vd
Now v1 = vcm +
2
vd
v2 = vcm −
2
⎛ v ⎞ ⎛ v ⎞
So v02 = (1.183) ⎜ vcm + d ⎟ − (1.691) ⎜ vcm − d ⎟
⎝ 2⎠ ⎝ 2⎠
Or v02 = 1.437vd − 0.508vcm ⇒ Ad = 1.437, Acm = −0.508
⎛ 1.437 ⎞
C M R RdB = 20 log10 ⎜ ⎟ ⇒ C M R RdB = 9.03 dB
⎝ 0.508 ⎠
11.46
KVL:

33. v1 = Vgs1 − Vgs 2 + v2
So v1 − v2 = Vgs1 − Vgs 2
KCL:
g mVgs1 + g mVgs 2 = 0 ⇒ Vgs1 = −Vgs 2
1 1
So Vgs1 = ( v1 − v2 ) , Vgs 2 = − ( v1 − v2 )
2 2
Now
v02 v02 − v01
+ = − g mVgs 2
RD RL
(1)
⎛ 1 1 ⎞ v01
= v02 ⎜ + ⎟−
⎝ RD RL ⎠ RL
v01 v01 − v02
+ = − g mVgs1
RD RL
(2)
⎛ 1 1 ⎞ v02
= v01 ⎜ + ⎟−
⎝ RD RL ⎠ RL
⎛ R ⎞
From (1): v01 = v02 ⎜ 1 + L ⎟ + g m RLVgs 2
⎝ RD ⎠
Substitute into (2):
⎛ R ⎞⎛ 1 1 ⎞ ⎛ 1 1 ⎞ v02
− g mVgs1 = v02 ⎜1 + L ⎟ ⎜ + ⎟ + g m RL ⎜ + ⎟ Vgs 2 −
⎝ RD ⎠ ⎝ RD RL ⎠ ⎝ RD RL ⎠ RL
⎛ R ⎞⎛ 1 ⎞ ⎛ 1 R 1 ⎞
− g m ⋅ ( v1 − v2 ) + g m ⎜ 1 + L ⎟ ⎜ ⎟ ( v1 − v2 ) = v02 ⎜ + L +
2 ⎟
⎝ RD ⎠ ⎝ 2 ⎠ ⎝ RD RD RD ⎠
1
⋅ g m RL
1 ⎛ RL ⎞ v02 ⎛ RL ⎞ v02
gm ⎜ ⎟ ( v1 − v2 ) = ⎜ 2 + ⎟ ⇒ Ad 2 = = 2
2 ⎝ RD ⎠ RD ⎝ RD ⎠ v1 − v2 ⎛ RL ⎞
⎜2+ ⎟
⎝ RD ⎠
1
− ⋅ g m RL
v01
From symmetry Ad 1 = = 2
v1 − v2 ⎛ RL ⎞
⎜2+ ⎟
⎝ RD ⎠
v02 − v01 g m RL
Then Av = =
v1 − v2 ⎛ RL ⎞
⎜2+ ⎟
⎝ RD ⎠
11.47

34. v1 − v2 = Vgs1 − Vgs 2 and g mVgs1 + g mVgs 2 = 0 ⇒ Vgs1 = −Vgs 2
Then v1 − v2 = −2Vgs 2
1
Or Vgs 2 = − ( v1 − v2 )
2
gm
v0 = − g mVgs 2 ( RD RL ) = ( RD RL ) ( v1 − v2 )
2
gm
Or Ad =
2
( RD RL )
11.48
Kn IQ
From Equation (11.64(a)), Ad = ⋅ RD
2
2
We need Ad = = 10
0.2
K n ( 0.5 )
Then 10 = ⋅ RD or K n ⋅ RD = 20
2
If we set RD = 20 k Ω, then K n = 1 mA / V 2
For this case VD = 10 − ( 0.25 )( 20 ) = 5 V
0.25
VGS = + 1 = 1.5 V
1
VDS ( sat ) = VGS − VTN = 1.5 − 1 = 0.5 V
Then vcm ( max ) = VD − VDS ( sat ) + VGS
= 5 − 0.5 + 1.5
Or vcm ( max ) = 6 V
11.49
Vd 1 = − g mVgs1 RD = − g m RD (V1 − Vs )
Vd 2 = − g mVgs 2 RD = − g m RD (V2 − Vs )
Now Vo = Vd 2 − Vd 1 = − g m RD (V2 − Vs ) − ( − g m RD (V1 − Vs ) )
Vo = g m RD (V1 − V2 )
Define V1 − V2 ≡ Vd
V
Then Ad = o = g m RD and Acm = 0
Vd
11.49
Ad = g m ( r02 r04 )
g m = 2 kn I DQ =2 ( 0.12 )( 0.075 )
= 0.1897 mA/V
1 1
r02 = = = 889 kΩ
λn I DQ ( 0.015 )( 0.075 )
1 1
r04 = = = 667 kΩ
λ p I DQ ( 0.02 )( 0.075 )
Ad = ( 0.1897 ) ( 889 667 ) ⇒ Ad = 72.3
11.50
(a)

35. ⎛ K′ ⎞⎛W ⎞ ⎛ 0.080 ⎞
⎟ (10 ) = 0.40 mA / V
2
K n1 = K n 2 = ⎜ n ⎟ ⎜ ⎟=⎜
⎝ 2 ⎠⎝ L ⎠ ⎝ 2 ⎠
ID 0.1
VGS1 = VGS 2 = + VTN = + 1 = 1.5 V
Kn 0.4
VDS1 ( sat ) = 1.5 − 1 = 0.5 V
For vCM = +3 V ⇒ VD1 = VD 2 = vCM − VGS 1 + VDS 1 ( sat )
= 3 − 1.5 + 0.5 ⇒ VD1 = VD 2 = 2 V
10 − 2
RD = ⇒ RD = 80 k Ω
0.1
(b)
1
Ad = g m RD and g m = 2 ( 0.4 )( 0.1) = 0.4 mA / V
2
1
Then Ad = ( 0.4 )( 80 ) = 16
2
16
C M R RdB = 45 ⇒ C M R R = 177.8 =
Acm
So Acm = 0.090
g m RD
Acm =
1 + 2 g m Ro
( 0.4 )(80 )
0.090 = ⇒ Ro = 443 k Ω
1 + 2 ( 0.4 ) Ro
If we assume λ = 0.01 V −1 for the current source transistor, then
1 1
ro = = = 500 k Ω
λ I Q ( 0.01)( 0.2 )
So the CMRR specification can be met by a 2-transistor current source.
⎛W ⎞ ⎛W ⎞
Let ⎜ ⎟ = ⎜ ⎟ = 1
⎝ L ⎠3 ⎝ L ⎠ 4
⎛ 0.080 ⎞ IQ 0.2
⎟ (1) = 0.040 mA / V and VGS 3 =
2
Then K n 3 = K n 4 = ⎜ + VTN = + 1 = 3.24 V
⎝ 2 ⎠ K n3 0.04
For vCM = −3 V , VD 3 = −3 − VGS1 = −3 − 1.5 = −4.5 V ⇒ VDS 3 ( min ) = −4.5 − ( −10 ) = 5.5 V > VDS 3 ( sat )
So design is OK.
⎛W ⎞
On reference side: For ⎜ ⎟ ≥ 1, VGS ( max ) = 3.24 V
⎝L⎠
20 − VGS 3 = 20 − 3.24 = 16.76 V
16.67
Then = 5.17 ⇒ We need six transistors in series.
3.24

36. 20 − 3.24
VGS = = 2.793 V
6
⎛ K′ ⎞⎛W ⎞
= ⎜ n ⎟ ⎜ ⎟ (VGS − VTN )
2
I REF
⎝ 2 ⎠⎝ L ⎠
⎛ 0.080 ⎞⎛ W ⎞ ⎛W ⎞
⎟⎜ ⎟ ( 2.793 − 1) ⇒ ⎜ ⎟ = 1.56 for each of the 6 transistors.
2
0.2 = ⎜
⎝ 2 ⎠⎝ L ⎠ ⎝L⎠
11.51
1
Ad = g m RD
2
gm = 2 Kn I D = 2 ( 0.25 )( 0.25) = 0.50 mA / V
1
Ad = ( 0.50 )( 3) = 0.75
2
From Problem 11.26

37. 5 (1 + δ )
V1 = VA = , V2 = VB = 2.5 V and V1 − V2 = 1.25δ
2+δ
Then
Vo 2 = Ad ⋅ (V1 − V2 ) = ( 0.75 )(1.25δ ) = 0.9375δ
So for −0.01 ≤ δ ≤ 0.01
−9.375 ≤ Vo 2 ≤ 9.375 mV
11.52
From previous results
v −v
Ad 1 = o 2 o1 = g m1 R1 = 2 K n1 I Q1 ⋅ R1 = 20
v1 − v2
vo3 1 1
and Ad 2 = = g m 3 R2 = 2 K n3 I Q 2 ⋅ R2 = 30
vo 2 − vo1 2 2
I Q1 R1 I Q 2 R2
Set = 5 V and = 2.5 V
2 2
Let I Q1 = I Q 2 = 0.1 mA
Then R1 = 100 k Ω, R2 = 50 k Ω
2
⎛ 0.06 ⎞ ⎛ W ⎞ ⎛ 20 ⎞ ⎛W ⎞ ⎛W ⎞
Then 2 ⎜ ⎟ ⎜ ⎟ ( 0.1) = ⎜ ⎟ ⇒ ⎜ ⎟ = ⎜ ⎟ = 6.67
⎝ 2 ⎠ ⎝ L ⎠1 ⎝ 100 ⎠ ⎝ L ⎠1 ⎝ L ⎠ 2
2
⎛ 0.060 ⎞ ⎛ W ⎞ ⎛ 2 ( 30 ) ⎞ ⎛W ⎞ ⎛W ⎞
and 2 ⎜ ⎟ ⎜ ⎟ ( 0.1) = ⎜ ⎟ ⇒ ⎜ ⎟ = ⎜ ⎟ = 240
⎝ 2 ⎠ ⎝ L ⎠3 ⎝ 50 ⎠ ⎝ L ⎠3 ⎝ L ⎠ 4
11.53
2
⎛ v ⎞
a. iD1 = I DSS ⎜ 1 − GS 1 ⎟
⎝ VP ⎠
2
⎛ v ⎞
iD 2 = I DSS ⎜ 1 − GS 2 ⎟
⎝ VP ⎠
⎛ v ⎞ ⎛ v ⎞
iD1 − iD 2 = I DSS ⎜1 − GS 1 ⎟ − I DSS ⎜ 1 − GS 2 ⎟
⎝ VP ⎠ ⎝ VP ⎠
I DSS
= ( vGS 2 − vGS1 )
VP
I DSS I DSS
=− ⋅ vd = ⋅ vd
VP ( −VP )
iD1 + iD 2 = I Q ⇒ iD 2 = I Q − iD1
( )
2 I DSS 2
iD1 − I Q − iD1 = ⋅ vd
( −VP )
2
iD1 − 2 iD1 ( I Q − iD1 ) + ( I Q − iD1 ) =
I DSS 2
⋅ vd
( −VP )
2
1⎡ ⎤
Then iD1 ( I Q − iD1 ) =
I
⎢ I Q − DSS 2 ⋅ vd ⎥
2
2⎢
⎣ ( −VP ) ⎦ ⎥
Square both sides

38. 2
1⎡ I ⎤
i − iD1 I Q + ⎢ I Q − DSS 2 ⋅ vd ⎥ = 0
2
D1
2
4⎢
⎣ ( −VP ) ⎥ ⎦
2
⎛ 1⎞⎡ I ⎤
I Q ± I − 4 ⎜ ⎟ ⎢ I Q − DSS 2 ⋅ vd ⎥
2 2
( −VP ) ⎥
Q
⎝ 4⎠⎢
⎣ ⎦
iD1 =
2
⎡ 2
⎤
1 2 ⎢ 2 2 I Q I DSS vd ⎛ I DSS vd ⎞ ⎥
2 2
IQ
iD1 = ± IQ − IQ − +⎜ ⎟
⎢ ( −VP ) ⎜ ( −VP ) ⎟ ⎥
2 2
2 2 ⎝ ⎠ ⎦
⎣
Use + sign
2
IQ 1 2 I Q I DSS 2 ⎛ I ⎞
iD1 = + ⋅ vd − ⎜ DSS 2 ⋅ vd ⎟
2
2 2 ( −VP )2 ⎜ ( −V ) ⎟
⎝ P ⎠
2 2
IQ 1 IQ 2 I DSS ⎛ I DSS ⎞ ⎛v ⎞
iD1 = + vd −⎜ ⎟ ⎜ d ⎟
2 2 ( −VP ) ⎜ I ⎟ V
IQ ⎝ Q ⎠ ⎝ P⎠
Or
2 2
iD1 1 ⎛ 1 ⎞ 2 I DSS ⎛ I DSS ⎞ ⎛ vd ⎞
= +⎜ ⎟ ⋅ vd −⎜ ⎟ ⎜ ⎟
I Q 2 ⎝ −2VP ⎜ I ⎟ V
⎠ IQ ⎝ Q ⎠ ⎝ P⎠
We had
iD 2 = I Q − iD1
Then
2 2
iD 2 1 ⎛ 1 ⎞ 2 I DSS ⎛ I DSS ⎞ ⎛ vd ⎞
= −⎜ ⎟ ⋅ vd −⎜ ⎟ ⎜ ⎟
I Q 2 ⎝ −2VP ⎜ I ⎟ V
⎠ IQ ⎝ Q ⎠ ⎝ P⎠
b.
If iD1 = I Q , then
2 2
1 ⎛ 1 ⎞ 2 I DSS ⎛ I DSS ⎞ ⎛ vd ⎞
1= +⎜ ⎟ ⋅ vd −⎜ ⎟ ⎜ ⎟
2 ⎝ −2VP ⎜ I ⎟ V
⎠ IQ ⎝ Q ⎠ ⎝ P⎠
2 2
2 I DSS ⎛ I DSS ⎞ ⎛ vd ⎞
VP = vd −⎜ ⎟ ⎜ ⎟
⎜ I ⎟ V
IQ ⎝ Q ⎠ ⎝ P⎠
Square both sides

39. ⎡ 2I ⎛I ⎞ ⎛ vd ⎞ ⎤
2 2
= v ⎢ DSS − ⎜ DSS ⎟ ⎜ ⎟ ⎥
2 2
VP
⎢ IQ ⎜ I ⎟ V
⎠ ⎝ P⎠ ⎥
d
⎣ ⎝ Q ⎦
2 2
⎛ I DSS ⎞ ⎛ 1 ⎞ 2 2 2 I DSS 2
⎟ ⎜ ⎟ ( vd ) −
2
⎜ ⋅ vd + VP =0
⎜ I ⎟ V
⎝ Q ⎠ ⎝ P⎠ IQ
2 2 2
2 I DSS ⎛ 2I ⎞ ⎛I ⎞ ⎛ 1 ⎞
⎟ ⎜ ⎟ (VP )
2
± ⎜ DSS ⎟ − 4 ⎜ DSS
⎜ I ⎟ ⎜ I ⎟ V
2
IQ ⎝ Q ⎠ ⎝ Q ⎠ ⎝ P⎠
vd = 2 2
⎛ 2I ⎞ ⎛ 1 ⎞
2 ⎜ DSS ⎟ ⎜ ⎟
⎜ IQ ⎟ ⎝ VP ⎠
⎝ ⎠
2 ⎛ IQ ⎞
vd = (VP ) ⎜
2
⎟
⎝ I DSS ⎠
1/ 2
⎛ IQ ⎞
Or vd = VP ⎜ ⎟
⎝ I DSS ⎠
c. For vd small,
IQ 1 IQ 2 I DSS
iD1 ≈ + ⋅ ⋅ vd
2 2 ( −VP ) IQ
diD1 1 IQ 2 I DSS
gf = = ⋅ ⋅
2 ( −VP )
vd → 0
d vd IQ
⎛ 1 ⎞ I Q I DSS
Or ⇒ g f ( max ) = ⎜ ⎟
⎝ −VP ⎠ 2
11.53
Ad = g m ( ro 2 Ro )
Want Ad = 400
From Example 11.15, ro 2 = 1 M Ω
Assuming that g m = 0.283 mA / V for the PMOS from Example 11.15, then Ro = 285 M Ω.
⎛ k ′ ⎞⎛ W ⎞
So 400 = g m (1000 285000 ) ⇒ g m = 0.4014 mA / V = 2 ⎜ n ⎟ ⎜ ⎟ I DQ
⎝ 2 ⎠ ⎝ L ⎠1
⎛ 0.080 ⎞ ⎛ W ⎞ ⎛W ⎞ ⎛W ⎞
0.04028 = ⎜ ⎟ ⎜ ⎟ ( 0.1) ⇒ ⎜ ⎟ = ⎜ ⎟ = 10.1
⎝ 2 ⎠ ⎝ L ⎠1 ⎝ L ⎠1 ⎝ L ⎠ 2
11.54
a.
I Q = I D1 + I D 2 ⇒ I Q = 1 mA
v0 = 7 = 10 − ( 0.5 ) RD ⇒ RD = 6 kΩ
b.
⎛ 1 ⎞ I Q ⋅ I DSS
g f ( max ) = ⎜ ⎟
⎝ −VP ⎠ 2
⎛ 1 ⎞ (1)( 2 )
g f ( max ) = ⎜ ⎟ ⇒ g f ( max ) = 0.25 mA/V
⎝ 4⎠ 2
c.
g R
Ad = m D = g f ( max ) ⋅ RD
2
Ad = ( 0.25 )( 6 ) ⇒ Ad = 1.5

40. 11.55
a.
−VGS − ( −5 )
2
⎛ V ⎞
IS = = ( 2 ) I DSS ⎜ 1 − GS ⎟
RS ⎝ VP ⎠
2
⎛ V ⎞
5 − VGS = ( 2 )( 0.8 )( 20 ) ⎜ 1 − GS ⎟
⎜ ( −2 ) ⎟
⎝ ⎠
⎛ 1 2 ⎞
5 − VGS = ( 2 )16 ⎜1 + VGS + VGS ⎟
⎝ 4 ⎠
2
8VGS + 33VGS + 27 = 0
−33 ± 1089 − 4 ( 8 )( 27 )
VGS =
2 (8)
= −1.125 V
5 − ( −1.125 )
IS =
20
= 0.306 mA
I D1 = I D 2 = 0.153 mA
vo 2 = 1.17 V
(b)
11.56
Equivalent circuit and analysis is identical to that in problem 11.36.
1
⋅ g m RL
Ad 2 = 2
⎛ RL ⎞
⎜2+ ⎟
⎝ RD ⎠
1
− ⋅ g m RL
Ad 1 = 2
⎛ RL ⎞
⎜2+ ⎟
⎝ RD ⎠
v02 − v01 g m RL
Av = =
vd ⎛ RL ⎞
⎜2+ ⎟
⎝ RD ⎠
11.57
(a)
Ad = g m ( ro 2 ro 4 )
0.1
gm = = 3.846 mA/V
0.026
120
ro 2 = = 1200 K
0.1
80
ro 4 = = 800 K
0.1
Ad = ( 3.846 ) (1200 800 )
Ad = 1846
(b)

41. For Ad = 923 = ( 3.846 ) (1200 800 RL )
480 RL
240 = 480 RL = ⇒ RL = 480 K
480 + RL
11.58
(a)
⎛ 2⎞
I Q = 250 μ A I REF = I Q ⎜ 1 + ⎟
⎝ β⎠
⎛ 2 ⎞
= 250 ⎜1 + ⎟ = 252.8 μ A
⎝ 180 ⎠
5 − ( 0.7 ) − ( −5 )
R1 = ⇒ R1 = 36.8 K
0.2528
(b)
0.125
Ad = g m ( ro 2 ro 4 ) gm = = 4.808 mA/V
0.026
150
ro 2 = = 1200 K
0.125
100
Ad = ( 4.808 ) (1200 800 ) ro 4 = = 800 K
0.125
Ad = 2308
(c)
2 (180 )( 0.026 )
Rid = 2rπ = ⇒ Rid = 74.9 K
0.125
Ro = ro 2 ro 4 = 1200 800 = 480 K = Ro
(d)
vcm ( max ) = 5 − 0.7 = 4.3 V
vcm ( min ) = 0.7 + 0.7 − 5 = −3.6 V
11.59
a.
⎛ IQ ⎞ ⎛ 1 ⎞
I 0 = I B3 + I B 4 ≈ 2 ⎜ ⎟ ⎜ ⎟
⎝ 2 ⎠⎝ β ⎠
I Q 0.2
I0 = = ⇒ I0 = 2 μ A
β 100
b.
V 100
r02 = r04 = A = = 1000 kΩ
I CQ 0.1
I CQ 0.1
gm = = = 3.846 mA/V
VT 0.026
Ad = g m ( r02 r04 ) = ( 3.846 ) (1000 1000 ) ⇒ Ad = 1923
c.
(
Ad = g m r02 r04 RL )
Ad = ( 3.846 ) (1000 1000 250 ) ⇒ Ad = 641
11.60
a.

42. Ad = g m ( r02 r04 RL )
I CQ IQ
gm = =
VT 2VT
V 125
r02 = A 2 =
I CQ I CQ
VA 4 80
r04 = =
I CQ I CQ
If I Q = 2 mA, then g m = 38.46 mA/V
r02 = 125 kΩ, r04 = 80 kΩ
So Ad = 38.46 ⎡125 80 200 ⎤
⎣ ⎦
Or Ad = 1508
For each gain of 1000. lower the current level
For I Q = 0.60 mA, I CQ = 0.30 mA
0.3
gm = = 11.54 mA/V
0.026
125
r02 = = 417 kΩ
0.3
80
r04 = = 267 kΩ
0.3
Ad = 11.54 ⎡ 417 267 200 ⎤ = 1036
⎣ ⎦
So I Q = 0.60 mA is adequate
b.
For V + = 10 V, VBE = VEB = 0.6 V
For VCB = 0, vcm ( max ) = V + − 2VEB = 10 − 2 ( 0.6 )
Or vcm ( max ) = 8.8 V
11.61
a. From symmetry.
0.1
VGS 3 = VGS 4 = VDS 3 = VDS 4 = +1
0.1
Or VDS 3 = VDS 4 = 2 V
0.1
VSG1 = VSG 2 = +1 = 2 V
0.1
VSD1 = VSD 2 = VSG1 − (VDS 3 − 10 )
= 2 − ( 2 − 10 )
Or VSD1 = VSD 2 = 10 V
b.
1 1
r0 n = = ⇒ 1 MΩ
λn I DQ ( 0.01)( 0.1)
1 1
r0 p = = ⇒ 0.667 MΩ
λP I DQ ( 0.015 )( 0.1)
g m = 2 K p (VSG + VTP )
= 2 ( 0.1)( 2 − 1) = 0.2 mA / V
Ad = g m ( ron rop ) = ( 0.2 ) (1000 667 ) ⇒ Ad = 80
(c)

43. IQ
I D 2 = I D1 = = 0.1 mA
2
1 1
ro 4 = = = 1000 k Ω
λn I D 4 ( 0.01)( 0.1)
1 1
ro 2 = = = 667 k Ω
λP I D 2 ( 0.015)( 0.1)
Ro = ro 2 ro 4 = 667 1000 = 400 k Ω
11.62
Ad = g m ( ro 4 ro 2 )
⎛ 0.08 ⎞
gm = 2 ⎜ ⎟ ( 2.5 )( 0.05 )
⎝ 2 ⎠
= 0.1414 mA/V
1
ro 4 = = 1000 K
( 0.02 )( 0.05 )
1
ro 2 = = 1333 K
( 0.015)( 0.05 )
Ad = ( 0.1414 ) (1000 1333)
Ad = 80.8
11.63
R04 = r04 ⎡1 + g m 4 ( R rπ 4 ) ⎤
⎣ ⎦
80
r04 = = 800 K
0.1
0.1
gm4 = = 3.846
0.026
(100 )( 0.026 )
rπ 4 =
0.1
= 26 K
R rπ 4 = 1 26 = 0.963 K
Assume β = 100
(100 )( 0.026 )
rπ 3 = = 26 kΩ
0.1
0.1
g m3 = = 3.846 mA/V
0.026
R04 = 800 ⎡1 + ( 3.846 )( 0.963) ⎤ ⇒ 3.763 MΩ
⎣ ⎦
⇒ R0 = 3.763MΩ
Then
Av = − g m ( r02 R0 )
120
r02 = = 1200 kΩ
0.1
0.1
gm = = 3.846 mA/V
0.026
Av = − ( 3.846 ) ⎡1200 3763⎤ ⇒ Av = −3499
⎣ ⎦
b.
For

44. 80
R = 0, r04 = = 800 kΩ
0.1
Av = − g m ( r02 r04 )
= − ( 3.846 ) ⎡1200 800 ⎤ ⇒ Av = −1846
⎣ ⎦
(c) For part (a), Ro = ( 3.763 1.2 ) = 0.910 M Ω
For part (b), Ro = (1.2 0.8 ) = 0.48 M Ω
11.64
IE5 I +I I +I
I B5 = = B3 B4 = C 3 C 4
1+ β 1+ β β (1 + β )
Now I C 3 + I C 4 ≈ I Q
IQ
So I B 5 ≈
β (1 + β )
IE6 I Q1
I B6 = =
1 + β β (1 + β )
For balance, we want I B 6 = I B 5
So that I Q1 = I Q
11.65
Resistance looking into drain of M4.
Vsg 4 ≅ I X R1
VX − Vsg 4
I X ± g m 4Vsg 4 =
r04
⎡ R ⎤ V
I X ⎢1 + g m 4 R1 + 1 ⎥ = X
⎣ r04 ⎦ r04
⎡ R ⎤
Or R0 = r04 ⎢1 + g m 4 R1 + 1 ⎥
⎣ r04 ⎦
a.

45. Ad = g m 2 ( ro 2 Ro )
g m 2 = 2 K n I DQ = 2 ( 0.080 )( 0.1)
= 0.179 mA / V
1 1
ro 2 = = = 667 k Ω
λn I DQ ( 0.015 )( 0.1)
g m 4 = 2 K P I DQ = 2 ( 0.080 )( 0.1)
= 0.179 mA / V
1 1
ro 4 = = = 500 k Ω
λ p I DQ ( 0.02 )( 0.1)
⎡ 1 ⎤
R0 = 500 ⎢1 + ( 0.179 )(1) + = 590.5 kΩ
⎣ 500 ⎥
⎦
Ad = ( 0.179 ) ⎡667 590.5⎤ ⇒ Ad = 56.06
⎣ ⎦
b.
When R1 = 0, R0 = r04 = 500 kΩ
Ad = ( 0.179 ) ⎡667 500 ⎤ ⇒ Ad = 51.15
⎣ ⎦
(c) For part (a), Ro = ro 2 Ro = 667 590.5 ⇒ Ro = 313 k Ω
For part (b), Ro = ro 2 ro 4 = 667 500 ⇒ Ro = 286 kΩ
11.66
Let β = 100, VA = 100 V

46. VA 100
ro 2 = = = 1000 k Ω
I CQ 0.1
Ro 4 = ro 4 [1 + g m RE ] where RE = rπ RE
′ ′
Now
(100 )( 0.026 )
rπ = = 26 k Ω
0.1
0.1
gm = = 3.846 mA / V
0.026
′
RE = 26 1 = 0.963 k Ω
Then Ro 4 = 1000 ⎡1 + ( 3.846 )( 0.963) ⎤ = 4704 k Ω
⎣ ⎦
Ad = g m ( ro 2 Ro 4 ) = 3.846 (1000 4704 ) ⇒ Ad = 3172
11.67
(a) For Q2, Q4
Vx − Vπ 4 V
(1) Ix = + g m 2Vπ 2 + g m 4Vπ 4 + x
ro 2 ro 4
Vx − Vπ 4 V
(2) g m 2Vπ 2 + = π4
ro 2 rπ 4 rπ 2
(3) Vπ 4 = −Vπ 2
Vx ⎡ 1 1 ⎤
From (2) = Vπ 4 ⎢ + + gm2 ⎥
ro 2 ⎢
⎣ rπ 4 rπ 2 ro 2 ⎥
⎦

47. Now
⎛ β ⎞ ⎛ IQ
⎞ ⎛ 120 ⎞
IC 4 = ⎜ ⎟⎜ ⎟=⎜ ⎟ ( 0.5 ) = 0.496 mA
⎝ 1+ β ⎠⎝ 2 ⎠ ⎝ 121 ⎠
⎛ IQ ⎞ ⎛ 1 ⎞ ⎛ β ⎞ ⎛ 120 ⎞
IC 2 = ⎜ ⎟⎜ ⎟⎜ ⎟ = ( 0.5 ) ⎜ ⎟ ⇒ I C 2 = 0.0041 mA
⎜ (121)2 ⎟
⎝ 2 ⎠⎝ 1+ β ⎠⎝ 1+ β ⎠ ⎝ ⎠
So
(120 )( 0.026 )
rπ 2 = = 761 k Ω
0.0041
0.0041
gm2 = = 0.158 mA/V
0.026
100
ro 2 = ⇒ 24.4 M Ω
0.0041
(120 ) ( 0.026 )
rπ 4 = = 6.29 k Ω
0.496
0.496
gm4 = = 19.08 mA / V
0.026
100
ro 4 = = 202 k Ω
0.496
Now
Vx ⎡ 1 1 ⎤ Vx
= Vπ 4 ⎢ + + 0.158⎥ ⇒ which yields Vπ 4 =
ro 2 ⎢ 6.29 761 24400
⎣ ⎥
⎦ ( 0.318) ro 2
From (1),
V V ⎛ 1 ⎞
I x = x + x + Vπ 4 ⎜ g m 4 − g m 2 − ⎟
ro 2 ro 4 ⎝ ro 2 ⎠
⎡ ⎛ 1 ⎞⎤
Ix ⎢ 1 ⎜ 19.08 − 0.158 − ⎟
1 24400 ⎠ ⎥
+⎝
V
=⎢ + ⎥ which yields Ro 2 = x = 135 k Ω
Vx ⎢ 24400 202 ( 0.318)( 24400 ) ⎥ Ix
⎢ ⎥
⎣ ⎦
80
Now ro 6 = = 160 k Ω
0.5
Then Ro = Ro 2 ro 6 = 135 160 ⇒ Ro = 73.2 k Ω
(b)
Δi
Ad = g m Ro where g m =
c c
vd / 2

48. vd
Δi = g m1Vπ 1 + g m 3Vπ 3 and Vπ 1 + Vπ 3 =
2
⎛V ⎞
Also ⎜ π 1 + g m1Vπ 1 ⎟ rπ 3 = Vπ 3
⎝ rπ 1 ⎠
⎛1+ β ⎞
So Vπ 1 ⎜ ⎟ rπ 3 = Vπ 3
⎝ rπ 1 ⎠
⎛ 121 ⎞
Or Vπ 1 ⎜ ⎟ ( 6.29 ) = Vπ 3 ≅ Vπ 1
⎝ 761 ⎠
v v
Then 2Vπ 1 = d ⇒ Vπ 1 = d
2 4
⎛v ⎞ ⎛v ⎞
So Δi = ( g m1 + g m 3 ) Vπ 1 = ( 0.158 + 19.08 ) ⎜ d ⎟ = 9.62 ⎜ d ⎟
⎝ 4⎠ ⎝ 2⎠
Δi
So g m =
c
= 9.62 ⇒ Ad = ( 9.62 )( 73.2 ) ⇒ Ad = 704
vd / 2
Now Rid = 2 Ri where Ri = rπ 1 + (1 + β ) rπ 3
Ri = 761 + (121)( 6.29 ) = 1522 k Ω
Then Rid = 3.044 M Ω
11.69
(a)
Ad = 100 = g m ( ro 2 ro 4 )
Let I Q = 0.5 mA
1 1
ro 2 = = = 200 k Ω
λn I D ( 0.02 )( 0.25 )
1 1
ro 4 = = = 160 k Ω
λP I D ( 0.025 )( 0.25 )
Then 100 = g m ( 200 160 ) ⇒ g m = 1.125 mA / V
⎛ K′ ⎞⎛W ⎞
gm = 2 ⎜ n ⎟ ⎜ ⎟ ID
⎝ 2 ⎠⎝ L ⎠
⎛ 0.080 ⎞ ⎛ W ⎞ ⎛W ⎞
1.125 = 2 ⎜ ⎟ ⎜ ⎟ ( 0.25 ) ⇒ ⎜ ⎟ = 31.6
⎝ 2 ⎠⎝ L ⎠ ⎝ L ⎠n
⎛W ⎞ ⎛W ⎞
Now ⎜ ⎟ somewhat arbitrary. Let ⎜ ⎟ = 31.6
⎝ L ⎠P ⎝ L ⎠P
11.70

49. Ad = g m ( ro 2 ro 4 )
P = ( I Q + I REF ) (V + − V − )
Let I Q = I REF
Then 0.5 = 2 I Q ( 3 − ( −3) ) ⇒ I Q = I REF = 0.0417 mA
1 1
ro 2 = = = 3205 k Ω
λn I D ( 0.015 )( 0.0208 )
1 1
ro 4 = = = 2404 k Ω
λP I D ( 0.02 )( 0.0208 )
Then
Ad = 80 = g m ( 3205 2404 ) ⇒ g m = 0.0582 mA/V
⎛ k ′ ⎞⎛ W ⎞
gm = 2 ⎜ n ⎟ ⎜ ⎟ I D
⎝ 2 ⎠ ⎝ L ⎠n
⎛ 0.080 ⎞⎛ W ⎞ ⎛W ⎞
0.0582 = 2 ⎜ ⎟⎜ ⎟ ( 0.0208 ) ⇒ ⎜ ⎟ = 1.02
⎝ 2 ⎠⎝ L ⎠ n ⎝ L ⎠n
11.71
Ad = g m ( ro 2 Ro )
≈ g m ro 2
1
ro 2 =
λn I D
1
= = 666.7 K
( 0.015)( 0.1)
Ad = 400 = g m ( 666.7 )
g m = 0.60 mA/V
⎛ k′ ⎞⎛ W ⎞
= 2 ⎜ n ⎟⎜ ⎟ ID
⎝ 2 ⎠⎝ L ⎠
⎛ 0.08 ⎞ ⎛ W ⎞
0.60 = 2 ⎜ ⎟ ⎜ ⎟ ( 0.1)
⎝ 2 ⎠⎝ L ⎠
⎛W ⎞
0.090 = 0.004 ⎜ ⎟
⎝L⎠
⎛W ⎞ ⎛W ⎞
⎜ ⎟ = ⎜ ⎟ = 22.5
⎝ L ⎠1 ⎝ L ⎠ 2
11.72

50. Ad = g m ( Ro 4 Ro 6 )
where
Ro 4 = ro 4 + ro 2 [1 + g m 4 ro 4 ]
Ro 6 = ro 6 + ro8 [1 + g m 6 ro 6 ]
We have
1
ro 2 = ro 4 = = 1667 k Ω
( 0.015 )( 0.040 )
1
ro 6 = ro8 = = 1250 k Ω
( 0.02 )( 0.040 )
⎛ 0.060 ⎞
gm4 = 2 ⎜ ⎟ (15 )( 0.040 ) = 0.268 mA/V
⎝ 2 ⎠
⎛ 0.025 ⎞
gm6 = 2 ⎜ ⎟ (10 )( 0.040 ) = 0.141 mA/V
⎝ 2 ⎠
Then
Ro 4 = 1667 + 1667 ⎡1 + ( 0.268 )(1667 ) ⎤ ⇒ 748 M Ω
⎣ ⎦
Ro 6 = 1250 + 1250 ⎡1 + ( 0.141)(1250 ) ⎤ ⇒ 222.8 M Ω
⎣ ⎦
(a)
Ro = Ro 4 Ro 6 = 748 222.8 ⇒ Ro = 172 M Ω
(b)
Ad = g m 4 ( Ro 4 Ro 6 ) = ( 0.268 )(172000 ) ⇒ Ad = 46096
11.73
Ad = g m ( ro 2 ro 4 )
1
ro 2 = ro 4 =
λ ID
1
= = 500 K
( 0.02 )( 0.1)
gm = 2 Kn I D = 2 ( 0.5)( 0.1)
= 0.4472 mA/V
Ad = ( 0.4472 ) ( 500 500 ) ⇒ Ad = 112
Ro = ro 2 ro 4 = 500 500 ⇒ Ro = 250 K
11.74
(a)
I DP = K p (VSG + VTP )
2
0.4
+ 1 = VSG 3 = 1.894 V
0.5
I DN = K n (VGS − VTN )
2
0.4
+ 1 = VGS 1 = 1.894 V
0.5
VDS1 ( sat ) = VGS1 − VTN = 1.894 − 1 = 0.894 V
V + = VSG 3 + VDS1 ( sat ) − VGS 1 + vCM
V + = 1.894 + 0.894 − 1.894 + 4 ⇒ V + = 4.89 V = −V −
(b)

51. Ad = g m ( ro 2 ro 4 )
1 1
ro 2 = ro 4 = = = 166.7 K
λ ID ( 0.015 )( 0.4 )
gm = 2 Kn I D = 2 ( 0.5 )( 0.4 ) = 0.8944 mA/V
Ad = ( 0.8944 ) (166.7 166.7 ) ⇒ Ad = 74.5
11.75
(a) For vcm = +2V ⇒ V + = 2.7 V
If I Q is a 2-transistor current source,
V − = vcm − 0.7 − 0.7
V − = −3.4 V ⇒ V + = −V − = 3.4 V
(b)
100
Ad = g m ( ro 2 ro 4 ) ro 2 = = 1000 K
0.1
60
ro 4 = = 600 K
0.1
0.1
gm = = 3.846 mA/V
0.026
Ad = ( 3.846 ) (1000 600 ) ⇒ Ad = 1442
11.76
(a) V + = −V − = 3.4 V
(b)
75
ro 2 = = 1250 K
0.06
40
ro 4 = = 666.7 K
0.06
0.06
gm = = 2.308 mA/V
0.026
Ad = ( 2.308 ) (1250 666.7 )
Ad = 1004
11.77
g m1 = 2 K n I Bias1 = 2 ( 0.2 )( 0.25 ) = 0.447 mA/V
I CQ 0.75
gm2 = = = 28.85 mA/V
VT 0.026
β VT (120 )( 0.026 )
rπ 2 = = = 4.16 kΩ
I CQ 0.75

52. i0 = g m1Vgs1 + g m 2Vπ 2
Vπ 2 = g m1Vgs1rπ 2 and vi = Vgs1 + Vπ 2
i0 = Vgs1 ( g m1 + g m 2 ⋅ g m1rπ 2 )
vi
vi = Vgs1 + g m1Vgs1rπ 2 and Vgs1 =
1 + g m1rπ 2
g m1 (1 + β )
i0 = vi ⋅
1 + g m1rπ 2
i0 g m1 (1 + β ) ( 0.447 )(121)
gm =
C
= =
vi 1 + g m1rπ 2 1 + ( 0.447 )( 4.16 )
⇒ g m = 18.9 mA/V
C
11.78
1 1
r0 ( M 2 ) = = = 500 kΩ
λn I DQ ( 0.01)( 0.2 )
VA 80
r0 ( Q2 ) = = = 400 kΩ
I CQ 0.2
g m ( M 2 ) = 2 K n I DQ = 2 ( 0.2 )( 0.2 )
= 0.4 mA/V
Ad = g m ( M 2 ) ⎡ r0 ( M 2 ) r0 ( Q2 ) ⎤
⎣ ⎦
= 0.4 ⎡500 400 ⎤ ⇒ Ad = 88.9
⎣ ⎦
If the IQ current source is ideal, Acm = 0 and C M RRdB = ∞
11.79
a.
b. Assume RL is capacitively coupled. Then

53. I CQ + I DQ = I Q
VBE 0.7
I DQ = = = 0.0875 mA
R1 8
I CQ = 0.9 − 0.0875 = 0.8125 mA
g m1 = 2 K P I DQ = 2 (1)( 0.0875 ) ⇒ g m1 = 0.592 mA/V
I CQ 0.8125
gm2 = = ⇒ g m 2 = 31.25 mA/V
VT 0.026
β VT (100 )( 0.026 )
rπ 2 = = ⇒ rπ 2 = 3.2 kΩ
I CQ 0.8125
c.
V0 = ( − g m1Vsg − g m 2Vπ 2 ) RL
Vi + Vsg = V0 ⇒ Vsg = V0 − Vi
Vπ 2 = ( g m1Vsg ) ( R1 rπ 2 )
V0 = − ⎡ g m1Vsg + g m 2 g m1Vsg ( R1 rπ 2 ) ⎤ RL
⎣ ⎦
V0 = − (V0 − Vi ) ⎣ g m1 + g m 2 g m1 ( R1 rπ 2 ) ⎦ RL
⎡ ⎤
⎡ g m1 + g m 2 g m1 ( R1 rπ 2 ) ⎦ RL
⎤
= ⎣
V0
Av =
Vi 1 + ⎡ g m1 + g m 2 g m1 ( R1 rπ 2 ) ⎤ RL
⎣ ⎦
We find
g m1 + g m 2 g m1 ( R1 rπ 2 ) = 0.592 + ( 31.25 )( 0.592 ) ( 8 3.2 )
= 42.88
( 42.88 )( RL )
Then Av =
1 + ( 42.88 )( RL )
11.80
a. Assume RL is capacitively coupled.
0.7
I DQ = = 0.0875 mA
8
I CQ = 1.2 − 0.0875 = 1.11 mA
g m1 = 2 K p I DQ = 2 (1)( 0.0875 ) ⇒ g m1 = 0.592 mA/V
I CQ 1.11
gm2 = = ⇒ g m 2 = 42.7 mA/V
VT 0.026
β VT (100 )( 0.026 )
rπ 2 = = ⇒ rπ 2 = 2.34 kΩ
I CQ 1.11
b.

54. Vsg = VX
I X = g m 2Vπ 2 + g m1Vsg
(g V
m1 sg )(R1 rπ 2 ) = Vπ 2
I X = VX ⎡ g m1 + g m 2 g m1 ( R1 rπ 2 ) ⎤
⎣ ⎦
VX 1
R0 = =
IX g m1 + g m 2 g m1 ( R1 rπ 2 )
1
= ⇒ R0 = 21.6 Ω
0.592 + ( 0.592 )( 42.7 ) ( 8 2.34 )
11.81
(a)
Vo − ( −Vπ )
(1) g m 2Vπ + =0
ro 2
Vo − ( −Vπ ) −Vπ −Vπ ⎛ 1 1⎞
(2) g m 2Vπ + = g m1Vi + + or 0 = g m1Vi − Vπ ⎜ + ⎟
ro 2 ro1 rπ ⎝ ro1 rπ ⎠
g m1Vi
Then Vπ =
⎛ 1 1⎞
⎜ + ⎟
⎝ ro1 rπ ⎠
From (1)

55. ⎛ 1 ⎞ Vo
⎜ g m 2 + ⎟ Vπ + =0
⎝ ro 2 ⎠ ro 2
⎛ 1 ⎞
⎜ gm2 + ⎟
⎛ 1 ⎞
Vo = −ro 2 ⎜ g m 2 + ⎟ Vπ = −ro 2 g m1Vi ⎝
ro 2 ⎠
⎝ ro 2 ⎠ ⎛ 1 1⎞
⎜ + ⎟
⎝ ro1 rπ ⎠
⎛ 1 ⎞
− g m1ro 2 ⎜ g m 2 + ⎟
V
Av = o = ⎝ ro 2 ⎠
Vi ⎛ 1 1⎞
⎜ + ⎟
⎝ ro1 rπ ⎠
Now
g m1 = 2 K n I Q = 2 ( 0.25)( 0.025 ) = 0.158 mA / V
IQ 0.025
gm2 = = = 0.9615 mA / V
VT 0.026
1 1
ro1 = = = 2000 k Ω
λ IQ ( 0.02 )( 0.025)
VA 50
ro 2 = = = 2000 k Ω
I Q 0.025
β VT (100 )( 0.026 )
rπ = = = 104 k Ω
IQ 0.025
Then
⎛ 1 ⎞
− ( 0.158 )( 2000 ) ⎜ 0.9615 + ⎟
Av = ⎝ 2000 ⎠
⇒ Av = −30039
⎛ 1 1 ⎞
⎜ + ⎟
⎝ 2000 104 ⎠
To find Ro; set Vi = 0 ⇒ g m1Vi = 0

56. Vx − ( −Vπ )
I x = g m 2Vπ +
ro 2
Vπ = − I x ( ro1 rπ )
Then
⎛ 1 ⎞ V
I x = ⎜ g m 2 + ⎟ ( − I x ) ( ro1 rπ ) + x
⎝ ro 2 ⎠ ro 2
Combining terms,
Vx ⎡ ⎛ 1 ⎞⎤
Ro = = ro 2 ⎢1 + ( ro1 rπ ) ⎜ g m 2 + ⎟ ⎥
Ix ⎣ ⎝ ro 2 ⎠ ⎦
⎡ ⎛ 1 ⎞⎤
= 2000 ⎢1 + ( 2000 104 ) ⎜ 0.9615 + ⎟ ⇒ Ro = 192.2 M Ω
⎣ ⎝ 2000 ⎠ ⎥
⎦
(b)
Vo − ( −Vgs 3 )
(1) g m 3Vgs 3 + =0
ro3
Vo − ( −Vgs 3 ) −Vgs 3 − ( −Vπ 2 ) ⎛ 1 ⎞ Vgs 3
(2) g m 3Vgs 3 + = g m 2Vπ 2 + or 0 = Vπ 2 ⎜ g m 2 + ⎟ −
ro3 ro 2 ⎝ ro 2 ⎠ ro 2
Vπ 2 −Vgs 3 − ( −Vπ 2 ) ( −Vπ 2 )
(3) + g m 2Vπ 2 + = g m1Vi +
rπ 2 ro 2 ro1
Vgs 3
From (2), Vπ 2 =
⎛ 1 ⎞
ro 2 ⎜ g m 2 + ⎟
⎝ ro 2 ⎠
Then
⎛ 1 1 1⎞ Vgs 3
(3) Vπ 2 ⎜ + gm2 + + ⎟ = g m1Vi +
⎝ rπ 2 ro 2 ro1 ⎠ ro 2
or

57. Vgs 3 ⎡ 1 1 1⎤ Vgs 3
⎢ + gm2 + + ⎥ = g m1Vi +
⎛ 1 ⎞ r
ro 2 ⎜ g m 2 + ⎟ ⎣ π 2
ro 2 ro1 ⎦ ro 2
⎝ ro 2 ⎠
Vgs 3 ⎡ 1 1 1 ⎤ Vgs 3
⎛ 1 ⎞⎣ ⎢104 + 0.9615 + 2000 + 2000 ⎥ = 0.9615Vi + 2000
2000 ⎜ 0.9615 + ⎦
⎟
⎝ 2000 ⎠
Then Vgs 3 = 1.83 × 105 Vi
⎛ 1 ⎞ −V ⎛ 1 ⎞
⎟ (1.83 ×10 ) Vi
5
From (1), ⎜ g m 3 + ⎟ Vgs 3 = o or Vo = −2000 ⎜ 0.158 +
⎝ ro 3 ⎠ ro3 ⎝ 2000 ⎠
V
Av = o = −5.80 × 107
Vi
To find Ro
Vx − ( −Vgs 3 )
(1) I x = g m 3Vgs 3 +
ro3
Vx − ( −Vgs 3 ) −Vgs 3 − ( −Vπ 2 )
(2) g m 3Vgs 3 + = g m 2Vπ 2 +
ro 3 ro 2
(3) Vπ 2 = − I x ( ro1 rπ 2 )
⎛ 1 ⎞ V
From (1) I x = Vgs 3 ⎜ g m 3 + ⎟ + x
⎝ ro 3 ⎠ ro3
⎛ 1 ⎞ Vx
I x = Vgs 3 ⎜ 0.158 + ⎟+
⎝ 2000 ⎠ 2000
V
Ix − x
So Vgs 3 = 2000
0.1585

58. From (2),
⎡ 1 1 ⎤ V ⎛ 1 ⎞
Vgs 3 ⎢ g m 3 + + ⎥ + x = Vπ 2 ⎜ g m 2 + ⎟
⎣ ro 3 ro 2 ⎦ ro 3 ⎝ ro 2 ⎠
⎡ 1 1 ⎤ Vx ⎛ 1 ⎞
Vgs 3 ⎢ 0.158 + + ⎥ + 2000 = Vπ 2 ⎜ 0.9615 + 2000 ⎟
⎣ 2000 2000 ⎦ ⎝ ⎠
⎡ I − Vx / 2000 ⎤ Vx
Then ⎢ x ⎥ ( 0.159 ) + 2000 = − I x ( 2000 104 ) ( 0.962 )
⎣ 0.1585 ⎦
V
We find Ro = x = 6.09 × 1010 Ω
Ix
11.82
Assume emitter of Q1 is capacitively coupled to signal ground.
⎛ 80 ⎞
I CQ = 0.2 ⎜ ⎟ = 0.1975 mA
⎝ 81 ⎠
0.2
I DQ = = 0.00247 mA
81
(80 )( 0.026 )
rπ = = 10.5 k Ω
0.1975
0.1975
g m ( Q1 ) = = 7.60 mA / V
0.026
gm ( M1 ) = 2 K n I D = 2 ( 0.2 )( 0.00247 )
g m ( M 1 ) = 0.0445 mA / V
Vπ
Vi = Vgs + Vπ and Vπ = g m ( M 1 ) Vgs rπ or Vgs =
g m ( M 1 ) rπ
⎛ 1 ⎞ Vi
Then Vi = Vπ ⎜ 1 +
⎜ g (M )r ⎟ or Vπ =
⎟
⎝ 1 π ⎠ ⎛ 1 ⎞
⎜1 +
m
⎜ g (M ) r ⎟ ⎟
⎝ m 1 π ⎠
V − g m ( Q1 ) RC
Vo = − g m ( Q1 ) Vπ RC ⇒ Av = o =
Vi ⎛ 1 ⎞
⎜1 +
⎜ g (M )r ⎟ ⎟
⎝ m 1 π ⎠
− ( 7.60 )( 20 )
Then Av = ⇒ Av = −48.4
⎛ 1 ⎞
⎜1 +
⎜ ( 0.0445 )(10.5 ) ⎟ ⎟
⎝ ⎠

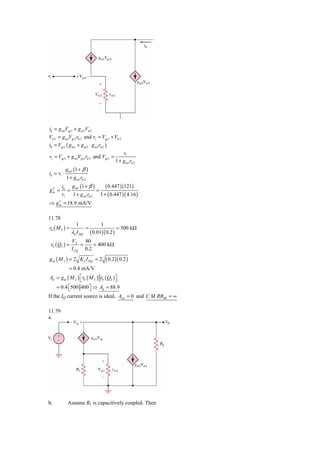
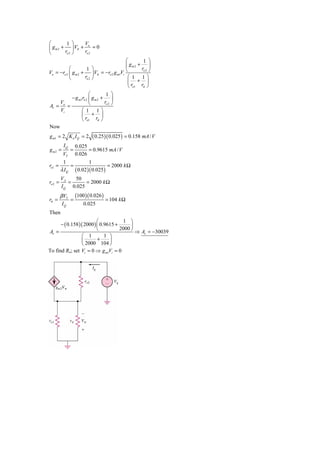
59. 11.83
Using the results from Chapter 4 for the emitter-follower:
⎡ rπ 9 + r07 R011 ⎤
⎢ rπ 8 + ⎥
1+ β
R0 = R4 || ⎢ ⎥
⎢ 1+ β ⎥
⎢ ⎥
⎣ ⎦
β VT (100 )( 0.026 )
rπ 8 = = = 2.6 kΩ
IC8 1
IC 8 1
IC 9 ≈ = = 0.01 mA
β 100
(100 )( 0.026 )
rπ 9 = = 260 kΩ
0.01
V 100
r07 = A = = 500 kΩ
I Q 0.2
VA 100
r011 = = = 500 kΩ
I Q 0.2
0.2
R011 = r011 [1 + g m RE ] , g m =
′ = 7.69
0.026
(100 ) ( 0.026 )
rπ 11 = = 13 kΩ
0.2
′
RE = 0.2 13 = 0.197 kΩ
R011 = 500 ⎡1 + ( 7.69 )( 0.197 ) ⎤ = 1257 kΩ
⎣ ⎦
Then
⎡ 260 + 500 1257 ⎤
⎢ 2.6 + ⎥
R0 = 5 || ⎢ 101 ⎥
⎢ 101 ⎥
⎢
⎣ ⎥
⎦
= 5 0.0863 ⇒ R0 = 0.0848 K ⇒ 84.8 Ω
11.84
Ri = rπ 1 + (1 + β ) rπ 2
(100 )( 0.026 )
rπ 2 = = 5.2 kΩ
0.5
(100 )( 0.026 ) (100 ) ( 0.026 )
2
rπ 1 = = = 520 kΩ
( 0.5 /100 ) 0.5
Ri = 520 + (101)( 5.2 ) ⇒ Ri ≅ 1.05 MΩ
rπ 3 + 50 (100 )( 0.026 )
R0 = 5 , rπ 3 = = 2.6 kΩ
101 1
2.6 + 50
R0 = 5 = 5 0.521 ⇒ R0 = 0.472 kΩ
101

60. ⎛V ⎞
V0 = − ⎜ π 3 + g m 3Vπ 3 ⎟ ( 5 )
⎝ rπ 3 ⎠
⎛1+ β ⎞
V0 = −Vπ 3 ⎜ ⎟ ( 5) (1)
⎝ rπ 3 ⎠
Vπ 3 (V − V )
= g m 2Vπ 2 + 0 π 3
rπ 3 50
⎛ 1 1 ⎞ V
g m 2Vπ 2 = Vπ 3 ⎜ + ⎟− 0 (2)
⎝ rπ 3 50 ⎠ 50
⎛V ⎞
Vπ 2 = ⎜ π 1 + g m1Vπ 1 ⎟ rπ 2
⎝ rπ 1 ⎠
(3)
⎛ 1+ β ⎞
= Vπ 1 ⎜ ⎟ rπ 2
⎝ rπ 1 ⎠
and
Vin = Vπ 1 + Vπ 2 (4)
0.5
gm2 = = 19.23 mA/V
0.026
Then
⎛ 101 ⎞
V0 = −Vπ 3 ⎜ ⎟ ( 5 ) ⇒ Vπ 3 = −V0 ( 0.005149 ) (1)
⎝ 2.6 ⎠
And
⎛ 1 1 ⎞ V
19.23Vπ 2 = −V0 ( 0.005149 ) ⎜ + ⎟− 0
⎝ 2.6 50 ⎠ 50 (2)
= −V0 ( 0.02208 )
Or Vπ 2 = −V0 ( 0.001148 )
And
Vπ 1 = Vin − Vπ 2 = Vin + V0 ( 0.001148 ) (4)
So
⎛ 101 ⎞
−V0 ( 0.001148 ) = ⎡Vin + V0 ( 0.001148 ) ⎤ ⎜
⎣ ⎦ 520 ⎟ ( 5.2 ) (3)
⎝ ⎠
V0
−V0 ( 0.001148 ) − V0 ( 0.001159 ) = Vin (1.01) ⇒ Av = = −438
Vin
11.85

61. 5
I2 = = 1 mA
5
1
VGS 2 = + 0.8 = 2.21 V
0.5
2.21 − ( −5 )
I1 = = 0.206 mA
35
V0 = ( g m 2Vgs 2 ) ( R2 r02 )
Vgs 2 = ( g m1Vsg1 ) ( r01 R1 ) − V0 and Vsg1 = −Vin
So Vgs 2 = − ( g m1Vin ) ( r01 R1 ) − V0
Then
V0 = g m 2 ( R2 r02 ) ⎡ − ( g m1Vin ) ( r01 R1 ) − V0 ⎤
⎣ ⎦
V0 − g m 2 ( R2 r02 ) g m1 ( r01 R1 )
Av = =
Vin 1 + g m 2 ( R2 r02 )
gm2 = 2 Kn2 I D 2 = 2 ( 0.5 )(1) = 1.414 mA / V
g m1 = 2 K p1 I D1 = 2 ( 0.2 )( 0.206 ) = 0.406 mA / V
1 1
r01 = = = 485 kΩ
λ1 I D1 ( 0.01)( 0.206 )
1 1
r02 = = = 100 kΩ
λ2 I D 2 ( 0.01)(1)
R2 r02 = 5 100 = 4.76 kΩ
R1 r01 = 35 485 = 32.6 kΩ
− (1.414 )( 4.76 )( 0.406 )( 32.6 )
Then Av =
1 + (1.414 )( 4.76 )
So ⇒ Av = −11.5
Output Resistance—From the results for a source follower in Chapter 6.
1 1
R0 = R2 r02 = 5 100
gm2 1.414
= 0.707 4.76
So R0 = 0.616 kΩ
11.86
a.

62. 5
R2 = ⇒ R2 = 10 kΩ
0.5
I D2 0.5
VSG 2 = − VTP 2 = + 1 = 2.41 V
K p2 0.25
5 − ( −2.41)
R1 = ⇒ R1 = 74.1 kΩ
0.1
b.
V0 = − ( g m 2Vsg 2 ) ( r02 R2 )
Vsg 2 = V0 − ⎡ − ( g m1Vgs1 ) ( r01 R1 ) ⎤ and Vgs1 = Vin
⎣ ⎦
V0 − ( g m 2 ) ( r02 R2 ) ( g m1 ) ( r01 R1 )
Av = =
Vin 1 + ( g m 2 ) ( r02 R2 )
g m1 = 2 K n1 I D1 = 2 ( 0.1)( 0.1) = 0.2 mA / V
gm2 = 2 K p 2 I D 2 = 2 ( 0.25)( 0.5) = 0.707 mA / V
1 1
r01 = = = 1000 kΩ
λ1 I D1 ( 0.01)( 0.1)
1 1
r02 = = = 200 kΩ
λ2 I D 2 ( 0.01)( 0.5 )
r02 R2 = 200 10 = 9.52 kΩ
r01 R1 = 1000 74.1 = 69.0 kΩ
− ( 0.707 )( 9.52 )( 0.2 )( 69 )
Then Av =
1 + ( 0.707 )( 9.52 )
So ⇒ Av = −12.0
1 1
R0 = R2 r02 = 10 200
gm2 0.707
= 1.414 9.52
Or R0 = 1.23 kΩ
11.87
a.
I C 2 = 0.25 mA
5−2
R= ⇒ R = 12 kΩ
0.25
v − VBE ( on ) 2 − 0.7
I C 3 = 02 ⇒ RE1 = ⇒ RE1 = 2.6 kΩ
RE1 0.5
5 − v03 5 − 3
RC = = ⇒ RC = 4 kΩ
IC 3 0.5
⎡ v03 − VBE ( on ) ⎤ − ( −5 )
IC 4 = ⎣ ⎦
RE 2
3 − 0.7 + 5
RE 2 = ⇒ RE 2 = 2.43 kΩ
3

63. b. Input resistance to base of Q3,
Ri 3 = rπ 3 + (1 + β ) RE1
(100 )( 0.026 )
rπ 3 = = 5.2 kΩ
0.5
Ri 3 = 5.2 + (101)( 2.6 ) = 267.8 kΩ
v 1
Ad 1 = 02 = g m 2 ( R Ri 3 )
vd 2
0.25
gm2 = = 9.62 mA/V
0.026
1
Ad 1 = ( 9.62 ) (12 267.8 ) ⇒ Ad 1 = 55.2
2
v − β ( RC Ri 4 )
Now 03 =
v02 rπ 3 + (1 + β ) RE1
where Ri 4 = rπ 4 + (1 + β ) RE 2
v0 (1 + β ) RE 2
and =
v03 rπ 4 + (1 + β ) RE 2
(100 )( 0.026 )
rπ 4 = = 0.867 kΩ
3
v0 (101)( 2.43)
= = 0.9965
v03 0.867 + (101)( 2.43)
Ri 4 = 0.867 + (101)( 2.43) = 246.3 kΩ
rπ 3 = 5.2 kΩ
v03 − (100 ) ( 4 246.3)
So = = −1.47
v02 5.2 + (101)( 2.6 )
v0
So Ad = = ( 55.2 )( 0.9965 )( −1.47 ) ⇒ Ad = −80.9
vd
c. Using Equation (11.32b)
− g m 2 ( R Ri 3 )
Acm1 =
2 (1 + β ) R0
1+
rπ 2
(100 )( 0.026 )
rπ 2 = = 10.4 kΩ
0.25
− ( 9.62 ) (12 267.8 )
Acm1 = = −0.0569 = Acm1
2 (101)(100 )
1+
10.4
⎛ v0 ⎞⎛ v03 ⎞
Then Acm = ⎜ ⎟⎜ ⎟ ⋅ Acm1
⎝ v03 ⎠⎝ v02 ⎠
= ( 0.9965 )( −1.47 )( −0.0569 ) ⇒ Acm = 0.08335
⎛ 80.9 ⎞
C M RRdB = 20 log10 ⎜ ⎟ ⇒ C M RRdB = 59.7 dB
⎝ 0.08335 ⎠
11.88
a.
10 − v01 10 − 2
RC1 = = ⇒ RC1 = 80 kΩ
I C1 0.1
10 − v04 10 − 6
RC 2 = = ⇒ RC 2 = 20 kΩ
IC 4 0.2

64. b.
v01 − v02
Ad 1 = = − g m1 ( RC1 rπ 3 )
vd
0.1
g m1 = = 3.846 mA/V
0.026
(180 )( 0.026 )
rπ 3 = = 23.4 kΩ
0.2
Ad 1 = − ( 3.846 ) ( 80 23.4 ) ⇒ Ad 1 = −69.6
v04 1
Ad 2 = = g m 4 RC 2
v01 − v02 2
0.2
gm4 = = 7.692 mA/V
0.026
1
Ad 2 = ( 7.692 )( 20 ) = 76.9
2
Then Ad = ( 76.9 )( −69.6 ) ⇒ Ad = −5352
11.89
a. Neglect the effect of r0 in determining the differential-mode gain.
v02 1
Ad 1 = = g m 2 ( RC Ri 3 ) where Ri 3 = rπ 3 + (1 + β ) RE
vd 2
− β RC 2
A2 =
rπ 3 + (1 + β ) RE
12 − 0.7 − ( −12 ) 23.3
I1 = = = 1.94 mA ≈ I C 5
R1 12
1
⋅ (1.94 )
gm2 = 2 = 37.3 mA/V
0.026
( 200 )( 0.026 )
rπ 3 =
IC 3
1
v02 = 12 − (1.94 )(8) = 4.24 V
2
4.24 − 0.7
IC 3 = = 1.07 mA
3.3
( 200 )( 0.026 )
rπ 3 = = 4.86 kΩ
1.07
Ri 3 = 4.86 + ( 201)( 3.3) = 668 kΩ
1
Ad 1 = ( 37.3) ⎣8 668⎦ = 147.4
⎡ ⎤
2
Then
Ad = Ad 1 ⋅ A2 = (147.4 )( −1.197 ) ⇒ Ad = −176
VA 80
R0 = r05 = = = 41.2 kΩ
I C 5 1.94
− g m 2 ( RC Ri 3 )
Acm1 =
2 (1 + β ) R0
1+
rπ 2
( 200 )( 0.026 )
rπ 2 = = 5.36 kΩ
1
⋅ (1.94 )
2

65. − ( 37.3) ( 8 668 )
Acm1 = = −0.09539
2 ( 201)( 41.2 )
1+
5.36
A2 = −1.197
Acm = ( −0.09539 )( −1.197 ) ⇒ Acm = 0.114
b.
vd = v1 − v2 = 2.015sin ω t − 1.985sin ω t
vd = 0.03sin ω t ( V )
v +v
vcm = 1 2 = 2.0sin ω t
2
v03 = Ad vd + Acm vcm
= ( −176 )( 0.03) + ( 0.114 )( 2 )
Or v03 = −5.052sin ω t
Ideal, Acm = 0
So
v03 = Ad vd = ( −176 )( 0.03)
v03 = −5.28sin ω t
c.
Rid = 2rπ 2 = 2 ( 5.36 ) ⇒ Rid = 10.72 kΩ
2 Ricm ≅ 2 (1 + β ) R0 (1 + β ) r0
VA 80
r0 = = = 82.5 kΩ
IC 2 1
⋅ (1.94 )
2
2 Ricm = ⎡ 2 ( 201)( 41.2 ) ⎤ ⎡( 201)( 82.5 ) ⎤
⎣ ⎦ ⎣ ⎦
= 16.6 MΩ 16.6 MΩ
So ⇒ Ricm = 4.15 MΩ
11.90
a.
24 − VGS 4
= kn (VGS 4 − VTh )
2
I1 =
R1
24 − VGS 4 = ( 55 )( 0.2 )(VGS 4 − 2 )
2
24 − VGS 4 = 11 (VGS 4 − 4VGS 4 + 4 )
2
2
11VGS 4 − 43VGS 4 + 20 = 0
( 43) − 4 (11)( 20 )
2
43 ±
VGS 4 = = 3.37 V
2 (11)
24 − 3.37
I1 = = 0.375 mA = I Q
55
⎛ 0.375 ⎞
v02 = 12 − ⎜ ⎟ ( 40 ) = 4.5 V
⎝ 2 ⎠
v02 − VGS 3
= I D 3 = kn (VGS 3 − VTh )
2
R5

66. 4.5 − VGS 3 = ( 0.2 ) ( 6 ) (VGS 3 − 4VGS 3 + 4 )
2
2
1.2VGS 3 − 3.8VGS 3 + 0.3 = 0
( 3.8) − 4 (1.2 ) ( 0.3)
2
3.8 ±
VGS 3 = = 3.09 V
2 (1.2 )
4.5 − 3.09
I D3 = = 0.235 mA
6
( 0.2 ) ⎛
0.375 ⎞
gm2 = 2 Kn I D2 = 2 ⎜ ⎟
⎝ 2 ⎠
= 0.387 mA/V
1 1
Ad 1 = g m 2 RD = ( 0.387 )( 40 ) ⇒ Ad 1 = 7.74
2 2
− g m 3 RD 2
A2 =
1 + g m 3 R5
g m3 = 2 K n I D3 = 2 ( 0.2 )( 0.235 )
= 0.434 mA/V
− ( 0.434 ) ( 4 )
A2 = = −0.482
1 + ( 0.434 )( 6 )
So Ad = Ad 1 ⋅ A2 = ( 7.74 ) ( −0.482 ) ⇒ Ad = −3.73
1 1
R0 = r05 = = = 133 kΩ
λ I Q ( 0.02 )( 0.375 )
− g m 2 RD − ( 0.387 ) ( 40 )
Acm1 = =
1 + 2 g m 2 R0 1 + 2 ( 0.387 ) (133)
= −0.149
Acm = ( −0.149 )( −0.482 ) ⇒ Acm = 0.0718
b.
vd = v1 − v2 = 0.3sin ω t
v +v
vcm = 1 2 = 2sin ω t
2
v03 = Ad vd + Acm vcm
= ( −3.73)( 0.3) + ( 0.0718 )( 2 ) ⇒ v03 = −0.975sin ω t ( V )
Ideal, Acm = 0
v03 = Ad vd = ( −3.73)( 0.3)
Or
⇒ v03 = −1.12sin ω t ( V )
11.91
The low-frequency, one-sided differential gain is

67. v02 1 ⎛ r ⎞
Av 2 = = g m RC ⎜ π ⎟
vd 2 ⎝ rπ + RB ⎠
1
⋅ β RC
= 2
rπ + RB
(100 )( 0.026 )
rπ = = 5.2 kΩ
0.5
1
⋅ (100 )(10 )
Av 2 = 2 ⇒ Av 2 = 87.7
5.2 + 0.5
CM = Cμ (1 + g m RC )
0.5
gm = = 19.23 mA/V
0.026
CM = 2 ⎡1 + (19.23)(10 ) ⎤ ⇒ CM = 387 pF
⎣ ⎦
1
fH =
2π ⎡ rπ RB ⎤ ( Cπ + CM )
⎣ ⎦
1
= So ⇒ f H = 883 kHz
2π ⎣5.2 0.5⎦ × 10 × ( 8 + 387 ) × 10−12
⎡ ⎤ 3
11.92
1 1
a. From Equation (11.117), f Z = =
2π R0 C0 2π ( 5 × 106 )( 0.8 × 10−12 )
Or f Z = 39.8 kHz
b. From Problem 11.69, f H = 883 kHz. From Equation (11.116(b)), the low-frequency
common- mode gain is
− g m RC
Acm =
⎡⎛ RB ⎞ 2 (1 + β ) R0 ⎤
⎢⎜ 1 + ⎟+ ⎥
⎣⎝ rπ ⎠ rπ ⎦
rπ = 5.2 kΩ, g m = 19.23 mA/V
So
− (19.23)(10 )
Acm =
⎡⎛ 0.5 ⎞ 2 (101) ( 5 × 106 ) ⎤
⎢⎜ 1 + ⎟+ ⎥
⎢⎝ 5.2 ⎠ 5.2 × 103 ⎥
⎣ ⎦
−4
= −9.9 × 10
⎛ 87.7 ⎞
C M RRdB = 20 log10 ⎜ −4 ⎟
= 98.9 dB
⎝ 9.9 × 10 ⎠

68. 11.93
gm
a. From Equation (7.72), fT =
2π ( Cπ + Cμ )
1
gm = = 38.46 mA/V
0.026
38.46 × 10−3
Then 800 × 106 =
2π ( Cπ + Cμ )
Or Cπ + Cμ = 7.65 × 10−12 F = 7.65 pF
And Cπ = 6.65 pF
CM = Cμ (1 + g m RC ) = 1 ⎡1 + ( 38.46 )(10 ) ⎤
⎣ ⎦
= 386 pF
1
fH =
2π ⎡ rπ RB ⎤ ( Cπ + CM )
⎣ ⎦
(120 )( 0.026 )
rπ = = 3.12 kΩ
1
1
fH =
2π ⎡3.12 1⎤ × 10 × ( 6.65 + 386 ) × 10−12
⎣ ⎦
3
Or f H = 535 kHz
1 1
b. From Equation (11.140), f Z = =
2π R0 C0 2π (10 × 106 )(10−12 )
Or f Z = 15.9 kHz
11.94
The differential-mode half circuit is:
⎛v ⎞ ⎛1⎞
g m ⎜ d ⎟ RC ⎜ ⎟ β RC
v02 = ⎝ 2⎠ or Av = ⎝ 2⎠
⎛1+ β ⎞ rπ + (1 + β ) RE
1+ ⎜ ⎟ RE
⎝ rπ ⎠
(100 )( 0.026 )
rπ = = 5.2 kΩ
0.5
⎛1⎞
⎜ ⎟ (100 )(10 ) 500
Av = ⎝ ⎠
2
=
5.2 + (101) RE 5.2 + (101) RE

69. a. For RE = 0.1 kΩ : Av = 32.7
b. For RE = 0.25 kΩ : Av = 16.4