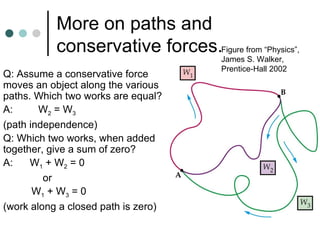
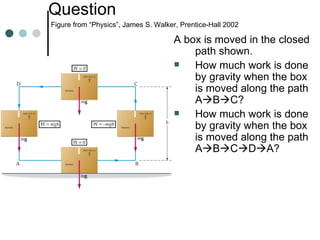
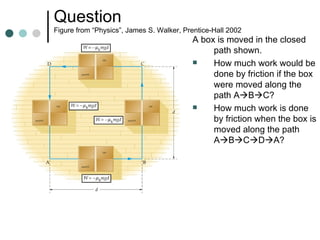
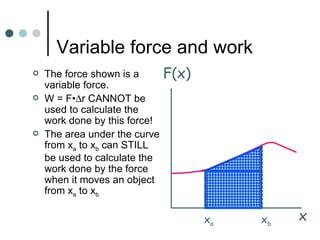
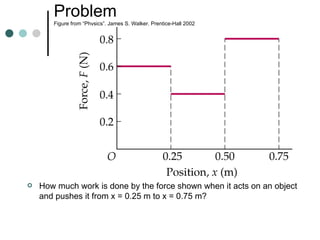
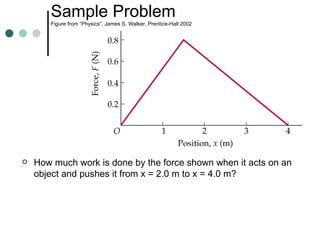
This document provides an overview of key concepts in work, energy, and power. It defines work and explains how to calculate work done by constant and variable forces. It introduces the concepts of kinetic and potential energy, and establishes the work-energy theorem. It distinguishes between conservative and non-conservative forces, and explains how the conservation of mechanical energy applies or does not apply in different situations. It also defines power and provides examples of calculating power.

1. Chapter 6 Work and Energy

2. Learning Objectives Work, energy, power Work and the work-energy theorem Students should understand the definition of work, including when it is positive, negative, or zero, so they can: Calculate the work done by a specified constant force on an object that undergoes a specified displacement. Relate the work done by a force to the area under a graph of force as a function of position, and calculate this work in the case where the force is a linear function of position. Use the scalar product operation to calculate the work performed by a specified constant force F on an object that undergoes a displacement in a plane.

3. Learning Objectives Work, energy, power Work and the work-energy theorem Students should understand and be able to apply the work-energy theorem, so they can: Calculate the change in kinetic energy or speed that results from performing a specified amount of work on an object. Calculate the work performed by the net force, or by each of the forces that make up the net force, on an object that undergoes a specified change in speed or kinetic energy. Apply the theorem to determine the change in an object’s kinetic energy and speed that results from the application of specified forces, or to determine the force that is required in order to bring an object to rest in a specified distance.

4. Learning Objectives Forces and potential energy Students should understand the concept of potential energy, so they can: Write an expression for the force exerted by an ideal spring and for the potential energy of a stretched or compressed spring. Calculate the potential energy of one or more objects in a uniform gravitational field.

5. Learning Objectives Conservation of energy Students should understand the concepts of mechanical energy and of total energy, so they can: Describe and identify situations in which mechanical energy is converted to other forms of energy. Analyze situations in which an object’s mechanical energy is changed by friction or by a specified externally applied force. Students should understand conservation of energy, so they can: Identify situations in which mechanical energy is or is not conserved. Apply conservation of energy in analyzing the motion of systems of connected objects, such as an Atwood’s machine. Apply conservation of energy in analyzing the motion of objects that move under the influence of springs.

6. Learning Objectives Power Students should understand the definition of power, so they can: Calculate the power required to maintain the motion of an object with constant acceleration (e.g., to move an object along a level surface, to raise an object at a constant rate, or to overcome friction for an object that is moving at a constant speed). Calculate the work performed by a force that supplies constant power, or the average power supplied by a force that performs a specified amount of work.

7. Table of Contents Work Done by a Constant Force The Work–Energy Theorem and Kinetic Energy Gravitational Potential Energy Conservative Versus Nonconservative Forces The Conservation of Mechanical Energy Nonconservative Forces and the Work–Energy Theorem Power Other Forms of Energy and the Conservation of Energy Work Done by a Variable Force

8. Chapter 6 Work & Energy Section 1: Work Done by a Constant Force

9. Work Work tells us how much a force or combination of forces changes the energy of a system. Work is the bridge between force ( a vector ) and energy ( a scalar ). W = F •  r = F  r cos  W: work F: force (N) (vector)  r : displacement (m) (vector)  : angle between force and displacement

10. Units of Work SI System: Joule (N m) 1 Joule of work is done when 1 N acts on a body moving it a distance of 1 meter British System: foot-pound (not used in Physics B) cgs System: erg (dyne-cm) (not used in Physics B) Atomic Level: electron-Volt (eV)

11. Force and direction of motion both matter in defining work! There is no work done by a force if it causes no displacement . Forces can do positive , negative , or zero work. When an box is pushed on a flat floor, for example… The normal force and gravity do no work , since they are perpendicular to the direction of motion. The person pushing the box does positive work , since she is pushing in the direction of motion. Friction does negative work , since it points opposite the direction of motion.

12. Question If a man holds a 50 kg box at arms length for 2 hours as he stands still, how much work does he do on the box? W = 0 J

13. Question If a man holds a 50 kg box at arms length for 2 hours as he walks 1 km forward, how much work does he do on the box? W = 0 J

14. Question If a man lifts a 50. kg box 2.0 meters , how much work does he do on the box? W = +980 J

15. Chapter 6 Work & Energy Section 2: Work-Energy Theorem & Kinetic Energy

16. Work and Energy Work changes mechanical energy! If an applied force does positive work on a system, it tries to increase mechanical energy. If an applied force does negative work, it tries to decrease mechanical energy. The two forms of mechanical energy are called potential and kinetic energy.

17. Question Jane uses a vine wrapped around a pulley to lift a 70. kg Tarzan to a tree house 9.0 meters above the ground. How much work does Jane do when she lifts Tarzan? How much work does gravity do when Jane lifts Tarzan?

18. Question Joe pushes a 10. kg box and slides it across the floor at constant velocity of 3.0 m/s. The coefficient of kinetic friction between the box and floor is 0.50. How much work does Joe do if he pushes the box for 15 meters? How much work does friction do as Joe pushes the box?

19. Question A father pulls his child in a little red wagon with constant speed. If the father pulls with a force of 16 N for 10.0 m, and the handle of the wagon is inclined at an angle of 60 o above the horizontal, how much work does the father do on the wagon?

20. Kinetic Energy Energy due to motion K = ½ m v 2 K: Kinetic Energy m: mass in kg v: speed in m/s Unit: Joules

21. Question A 10.0 g bullet has a speed of 1.2 km/s. What is the kinetic energy of the bullet? What is the bullet’s kinetic energy if the speed is halved? What is the bullet’s kinetic energy if the speed is doubled?

22. The Work-Energy Theorem The net work due to all forces equals the change in the kinetic energy of a system. W net =  K W net : work due to all forces acting on an object  K: change in kinetic energy (K f – K i )

23. Question An 15.0-g acorn falls from a tree and lands on the ground 10.0 m below with a speed of 11.0 m/s. What would the speed of the acorn have been if there had been no air resistance? Did air resistance do positive, negative or zero work on the acorn? Why?

24. Question An 15.0-g acorn falls from a tree and lands on the ground 10.0 m below with a speed of 11.0 m/s. How much work was done by air resistance? What was the average force of air resistance?

25. Chapter 6 Work & Energy Section 3: Gravitational Potential Energy

26. Potential energy Energy of position or configuration “ Stored” energy For gravity: U g = mgh m: mass g: acceleration due to gravity h: height above the “zero” point For springs: U s = ½ k x 2 (Chapter 10) k: spring force constant x: displacement from equilibrium position

27. Chapter 6 Work & Energy Section 4 Conservative vs non-conservative forces

28. Force types Forces acting on a system can be divided into two types according to how they affect potential energy. Conservative forces can be related to potential energy changes. Non-conservative forces cannot be related to potential energy changes. So, how exactly do we distinguish between these two types of forces?

29. Conservative forces Work is path independent . Work can be calculated from the starting and ending points only. The actual path is ignored in calculations. Work along a closed path is zero . If the starting and ending points are the same, no work is done by the force. Work changes potential energy . Examples: Gravity Spring force Ch 10 Conservation of mechanical energy holds!

30. Conservative forces and Potential energy W c = -  U If a conservative force does positive work on a system, potential energy is lost. If a conservative force does negative work, potential energy is gained. For gravity W g = -  U g = -(mgh f – mgh i ) For springs W s = -  U s = -(½ k x f 2 – ½ k x i 2 )

31. More on paths and conservative forces. Q: Assume a conservative force moves an object along the various paths. Which two works are equal? A: W 2 = W 3 (path independence) Q: Which two works, when added together, give a sum of zero? A: W 1 + W 2 = 0 or W 1 + W 3 = 0 (work along a closed path is zero) Figure from “Physics”, James S. Walker, Prentice-Hall 2002

32. Question Figure from “Physics”, James S. Walker, Prentice-Hall 2002 A box is moved in the closed path shown. How much work is done by gravity when the box is moved along the path A  B  C? How much work is done by gravity when the box is moved along the path A  B  C  D  A?

33. Question A diver drops to the water from a height of 40.0 m, his gravitational potential energy decreases by 25,000 J. How much does the diver weigh?

34. Chapter 6 Work & Energy Section 5: The Conservation of Mechanical Energy

35. Law of Conservation of Energy In any isolated system, the total energy remains constant. Energy can neither be created nor destroyed, but can only be transformed from one type of energy to another. Not true for nuclear reactions (Unit 11)

36. Law of Conservation of Mechanical Energy E = K + U = Constant K: Kinetic Energy (1/2 mv 2 ) U: Potential Energy (gravity or spring)  E =  U +  K = 0  K: Change in kinetic energy  U: Change in gravitational or spring potential energy

37. Question Problem copyright “Physics”, James S. Walker, Prentice-Hall 2002 A 0.21 kg apple falls from a tree to the ground, 4.0 m below. Ignoring air resistance, determine the apple’s gravitational potential energy, U, kinetic energy, K, and total mechanical energy, E, when its height above the ground is each of the following: 4.0 m, 2.0 m, and 0.0 m. Take ground level to be the point of zero potential energy.

38. Chapter 6 Work & Energy Section 6: Nonconservative Forces and the Work–Energy Theorem

39. Non-conservative forces Work is path dependent . Knowing the starting and ending points is not sufficient to calculate the work. Work along a closed path is NOT zero . Work changes mechanical energy . Examples: Friction Drag (air resistance) Conservation of mechanical energy does not hold!

40. Work done by non-conservative forces W net = W c + W nc Net work is done by conservative and non-conservative forces W c = -  U Potential energy is related to conservative forces only! W net =  K Kinetic energy is related to net force (work-energy theorem)  K = -  U + W nc From substitution W nc =  U +  K =  E Nonconservative forces change mechanical energy. If nonconservative work is negative, as it often is, the mechanical energy of the system will drop.

41. Question Figure from “Physics”, James S. Walker, Prentice-Hall 2002 A box is moved in the closed path shown. How much work would be done by friction if the box were moved along the path A  B  C? How much work is done by friction when the box is moved along the path A  B  C  D  A?

42. Chapter 6 Work & Energy Section 7 Power

43. Power Power is the rate of which work is done. P = W/  t P = F(v) W: work in Joules  t: elapsed time in seconds When we run upstairs, t is small so P is big. When we walk upstairs, t is large so P is small.

44. Unit of Power SI unit for Power is the Watt. 1 Watt = 1 Joule/s Named after the Scottish engineer James Watt (1776-1819) who perfected the steam engine. British system horsepower 1 hp = 746 W

45. How We Buy Energy… The kilowatt-hour is a commonly used unit by the electrical power company. Power companies charge you by the kilowatt-hour (kWh), but this not power, it is really energy consumed. 1 kW = 1000 W 1 h = 3600 s 1 kWh = 1000J/s • 3600s = 3.6 x 106J

46. Question A man runs up the 1600 steps of the Empire State Building in 20 minutes seconds. If the height gain of each step was 0.20 m, and the man’s mass was 80.0 kg, what was his average power output during the climb?

47. Question Calculate the power output of a 0.10 g fly as it walks straight up a window pane at 2.0 cm/s.

48. Chapter 6 Work & Energy Section 8: Other Forms of Energy and the Law of Conservation of Energy

49. Law of Conservation of Energy E = U + K + E int - W nc = Constant E int is thermal energy.  U +  K +  E int - W nc = 0 Mechanical energy may be converted to and from heat.

50. Question Problem copyright “Physics”, James S. Walker, Prentice-Hall 2002 Catching a wave, a 72-kg surfer starts with a speed of 1.3 m/s, drops through a height of 1.75 m, and ends with a speed of 8.2 m/s. How much non-conservative work was done on the surfer?

51. Question Problem copyright “Physics”, James S. Walker, Prentice-Hall 2002 A 1.75-kg rock is released from rest at the surface of a pond 1.00 m deep. As the rock falls, a constant upward force of 4.10 N is exerted on it by water resistance. Calculate the nonconservative work, W nc , done by the water resistance on the rock, the gravitational potential energy of the system, U, the kinetic energy of the rock, K, and the total mechanical energy of the system, E, for the following depths below the water’s surface: d = 0.00 m, d = 0.500 m, d = 1.00 m. Let potential energy be zero at the bottom of the pond.

52. Chapter 6 Work & Energy Section 9: Work done by variable forces

53. Constant force and work The force shown is a constant force. W = F •  r can be used to calculate the work done by this force when it moves an object from x a to x b . The area under the curve from x a to x b can also be used to calculate the work done by the force when it moves an object from x a to x b F(x) x x a x b

54. Variable force and work The force shown is a variable force. W = F •  r CANNOT be used to calculate the work done by this force! The area under the curve from x a to x b can STILL be used to calculate the work done by the force when it moves an object from x a to x b F(x) x x a x b

55. Problem Figure from “Physics”, James S. Walker, Prentice-Hall 2002 How much work is done by the force shown when it acts on an object and pushes it from x = 0.25 m to x = 0.75 m?

56. Sample Problem Figure from “Physics”, James S. Walker, Prentice-Hall 2002 How much work is done by the force shown when it acts on an object and pushes it from x = 2.0 m to x = 4.0 m?

57. END