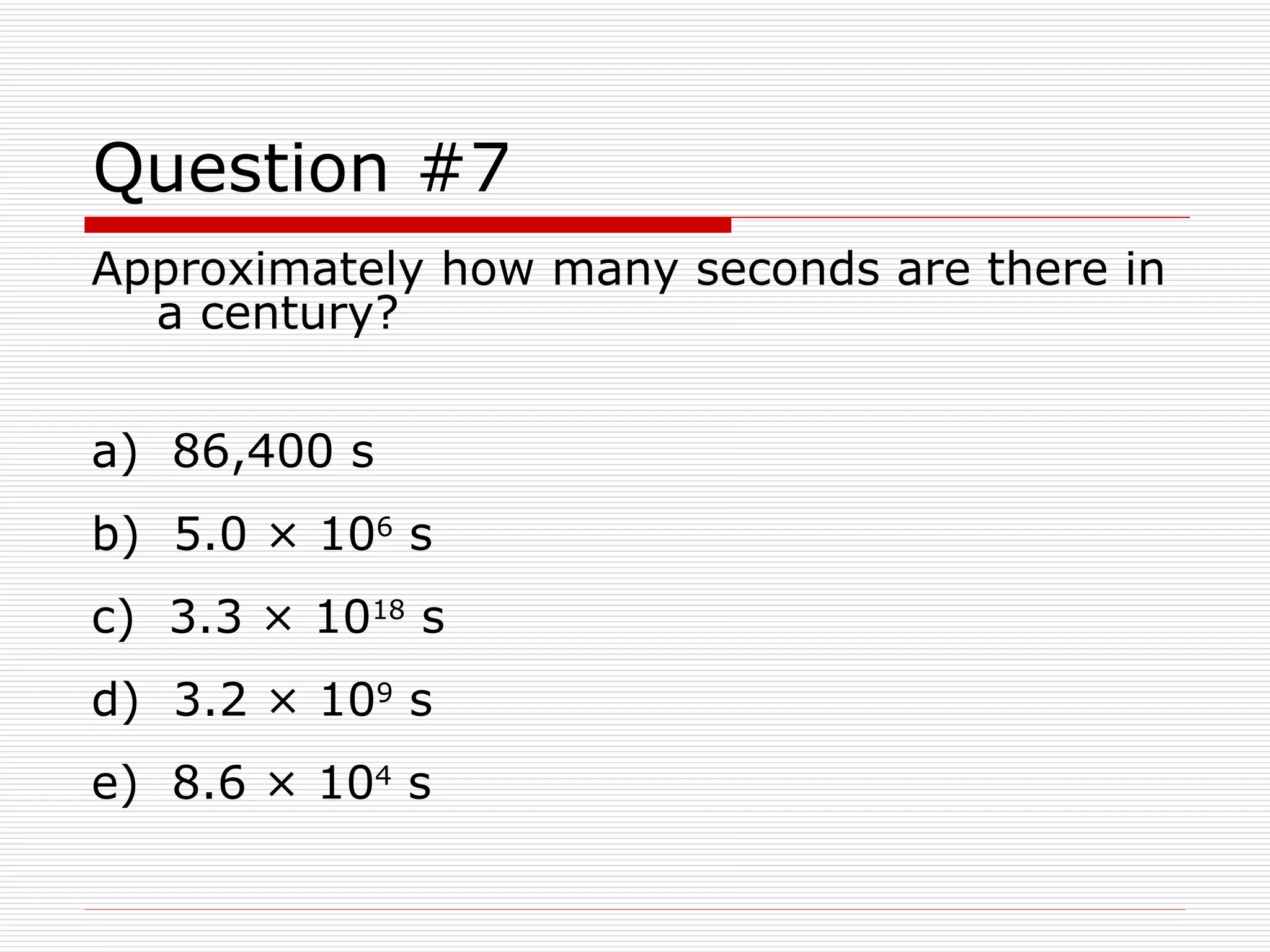
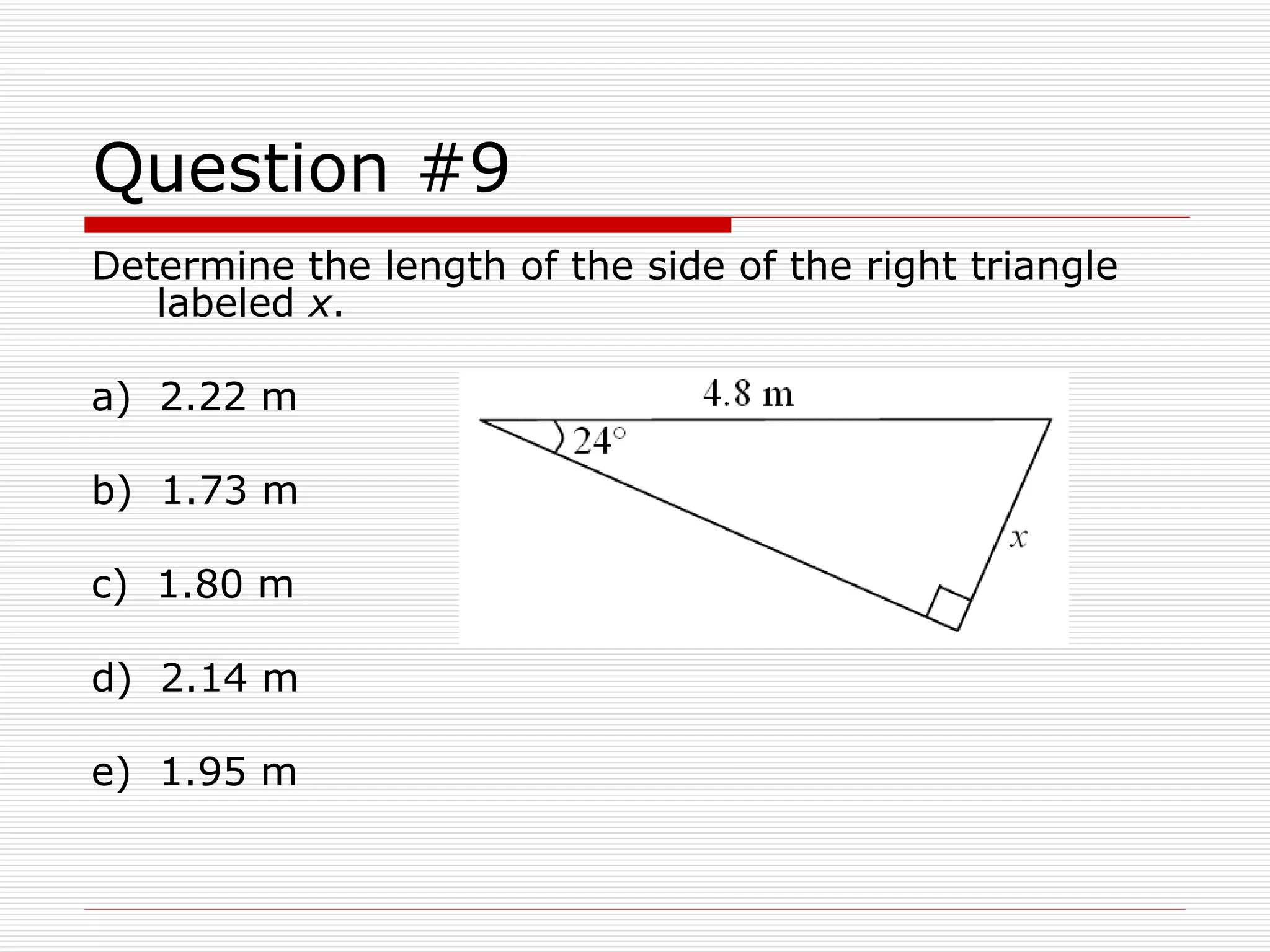
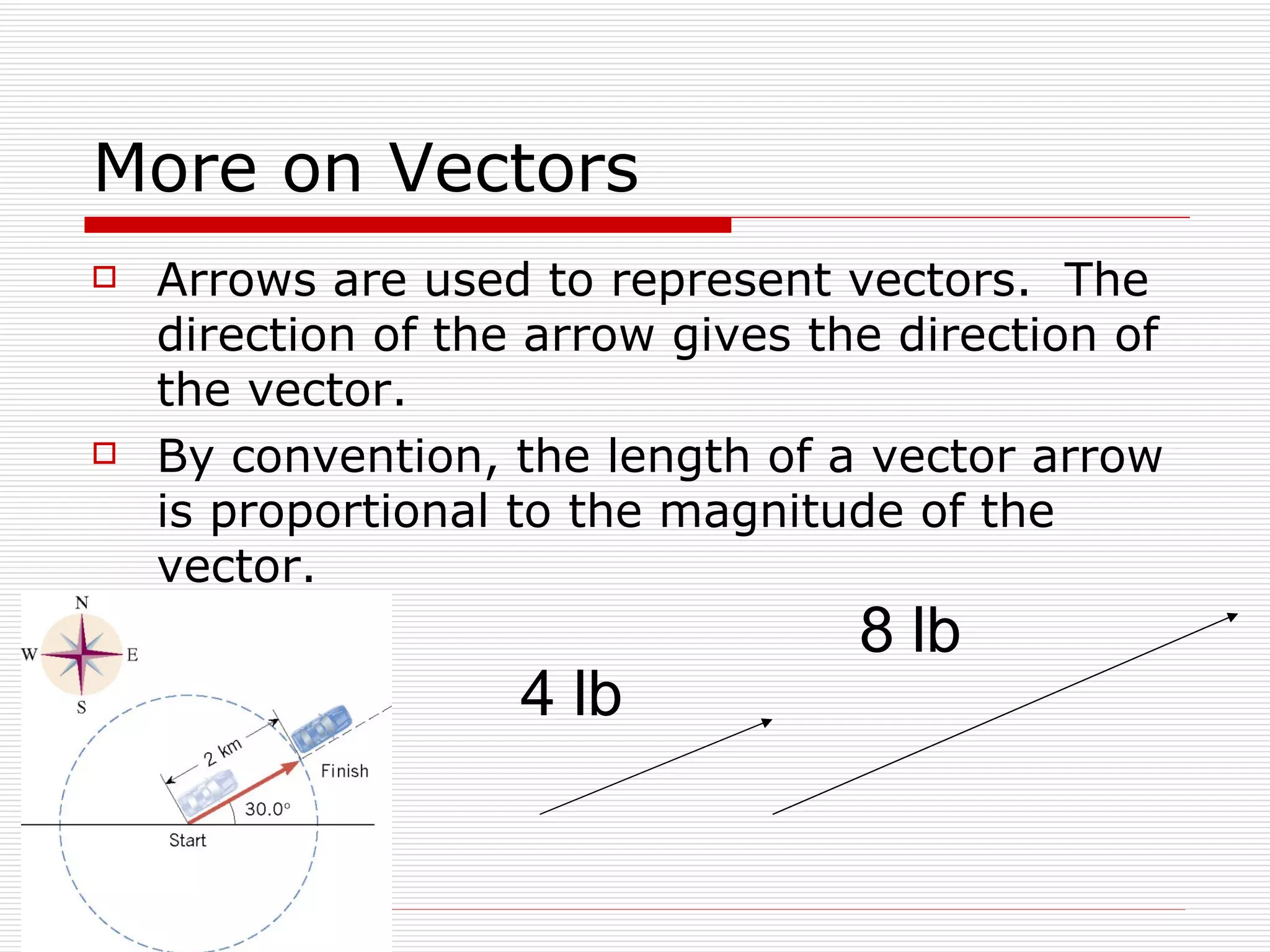
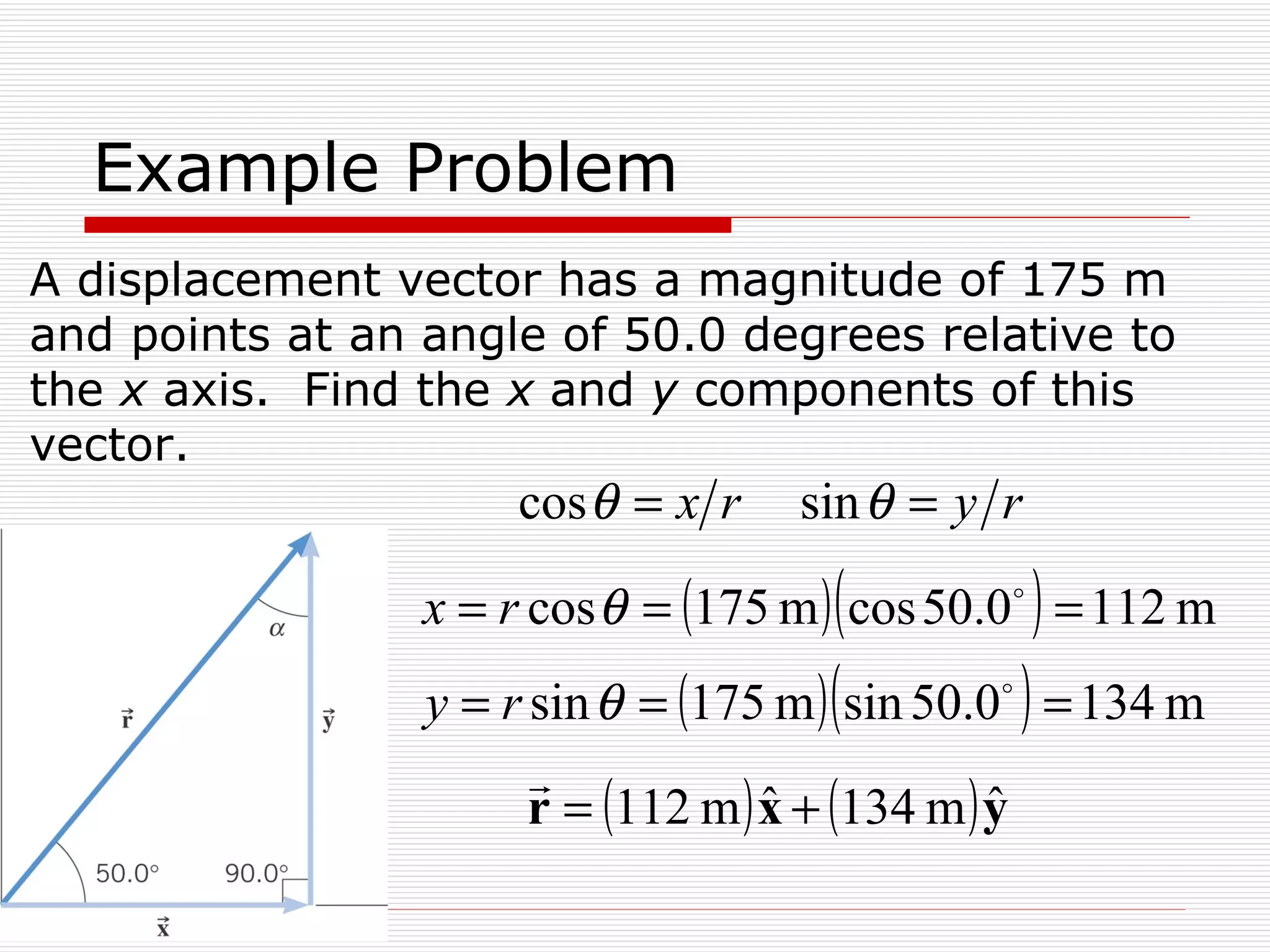
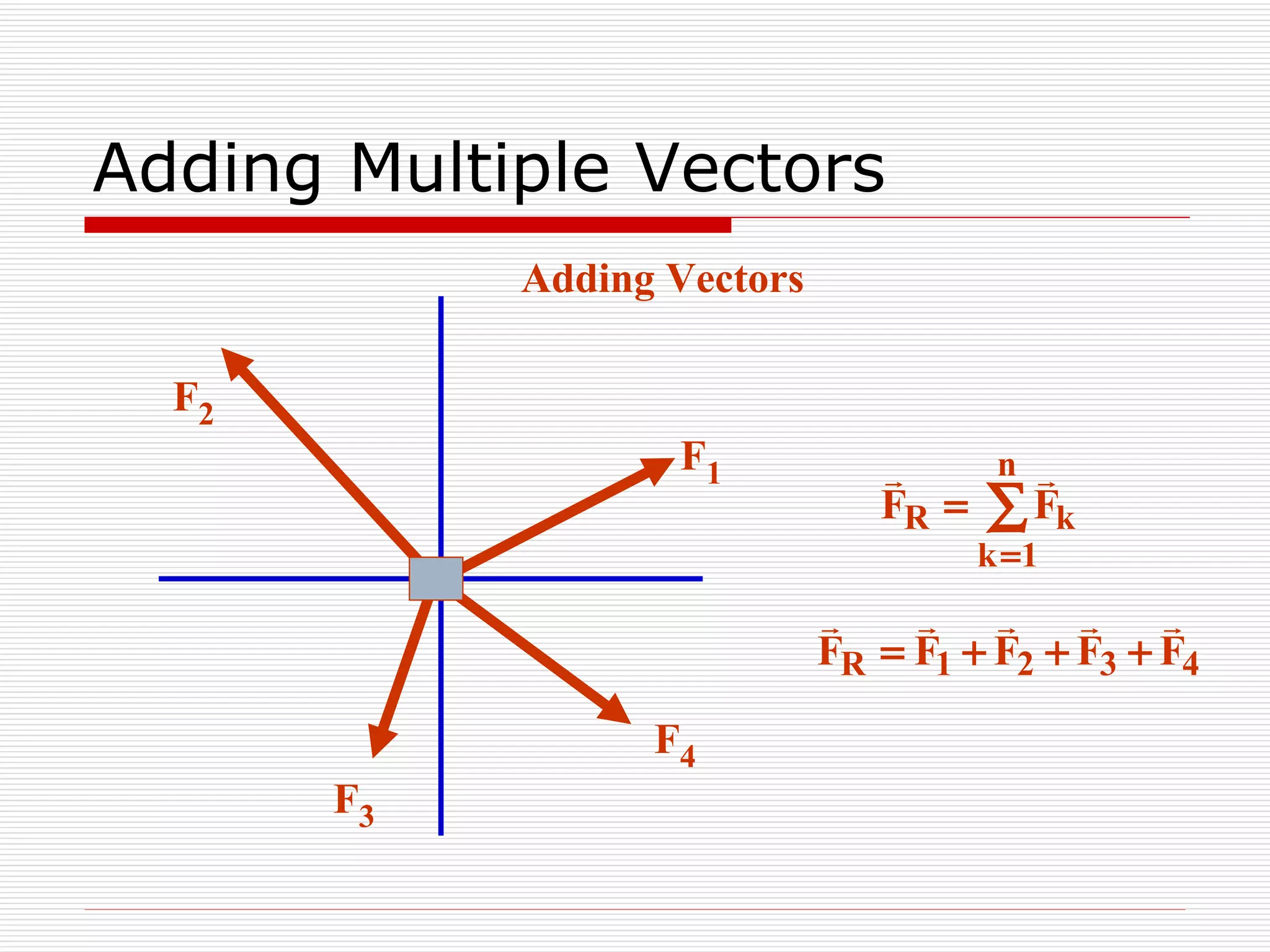
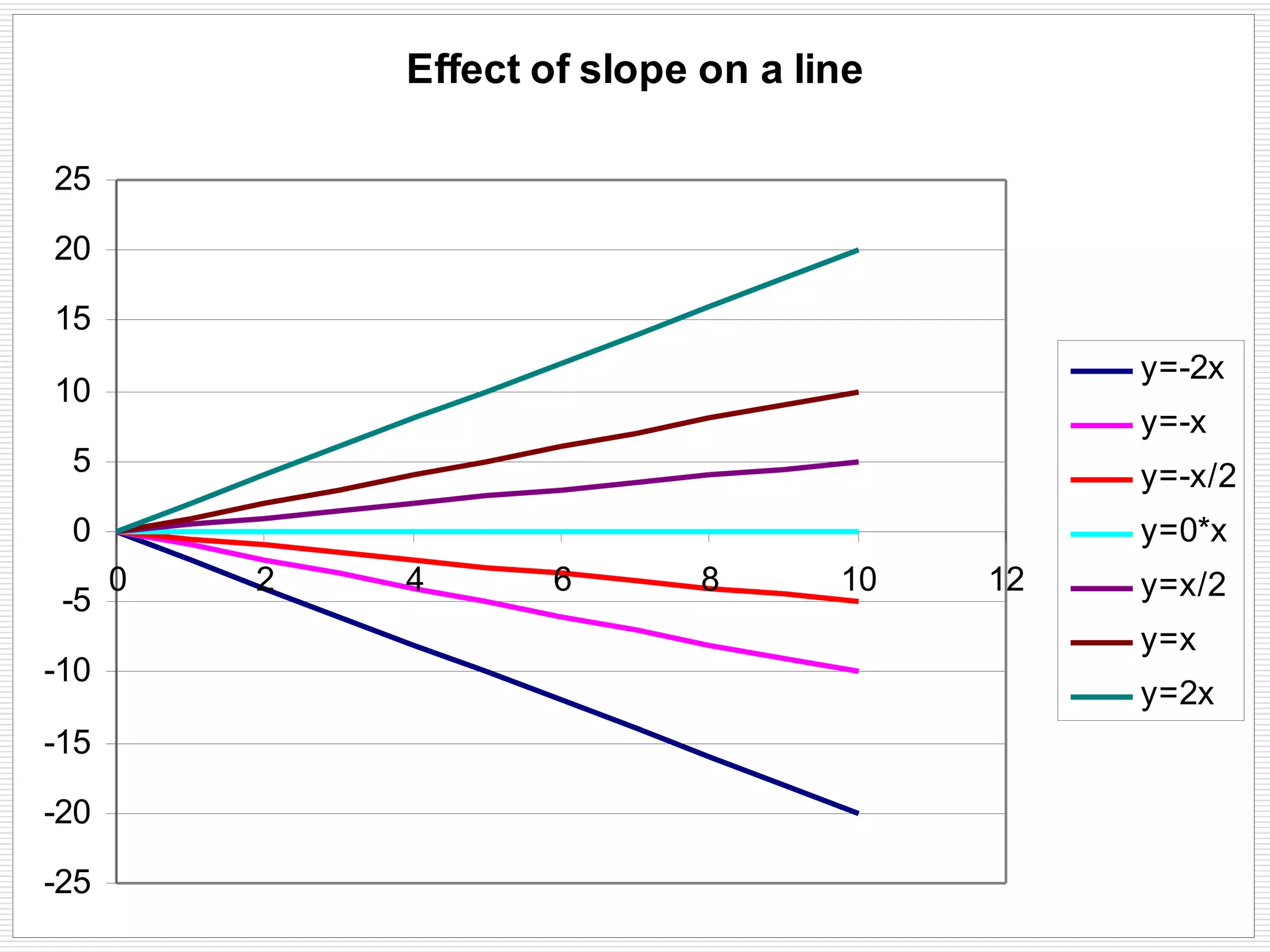
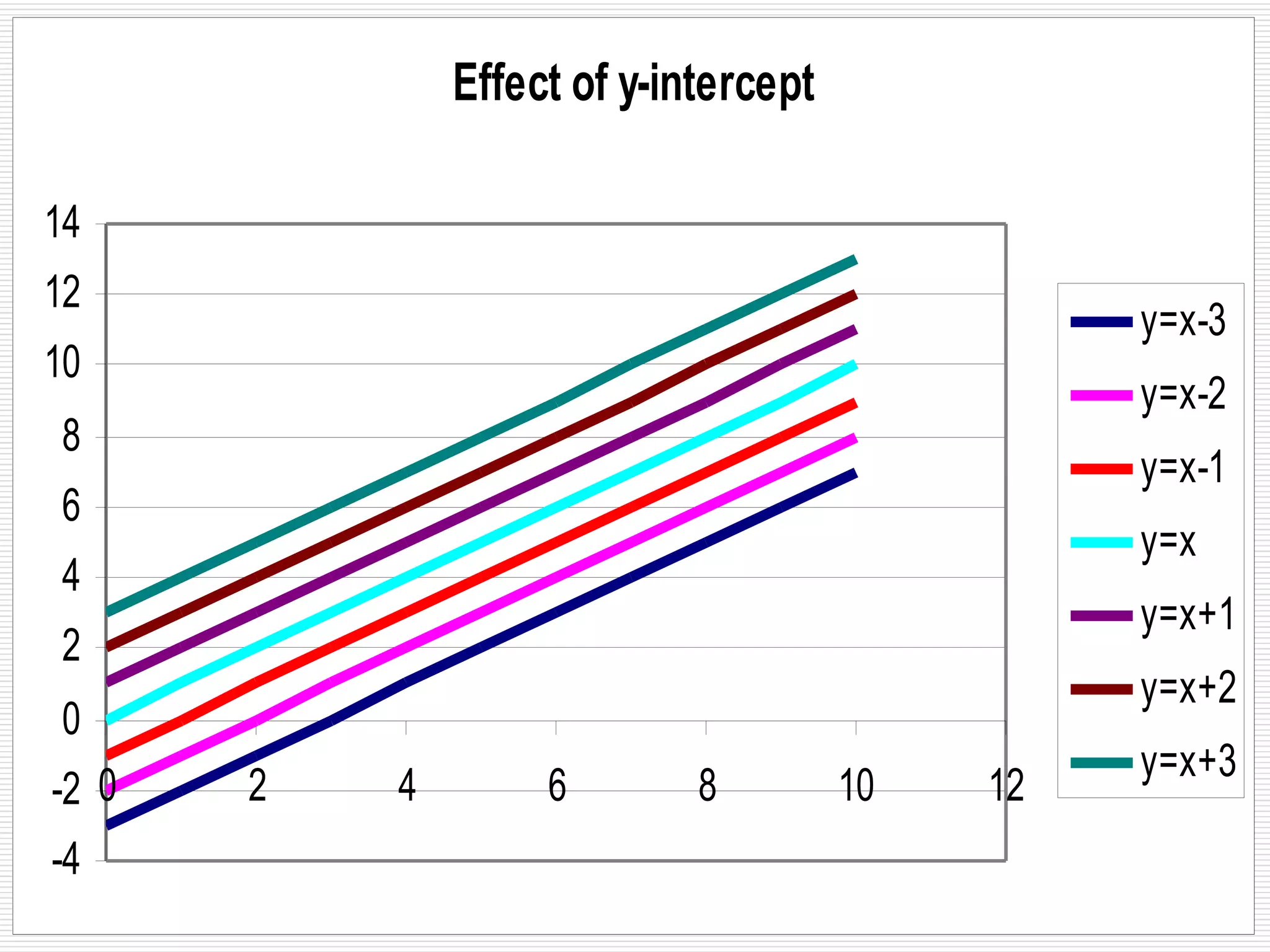
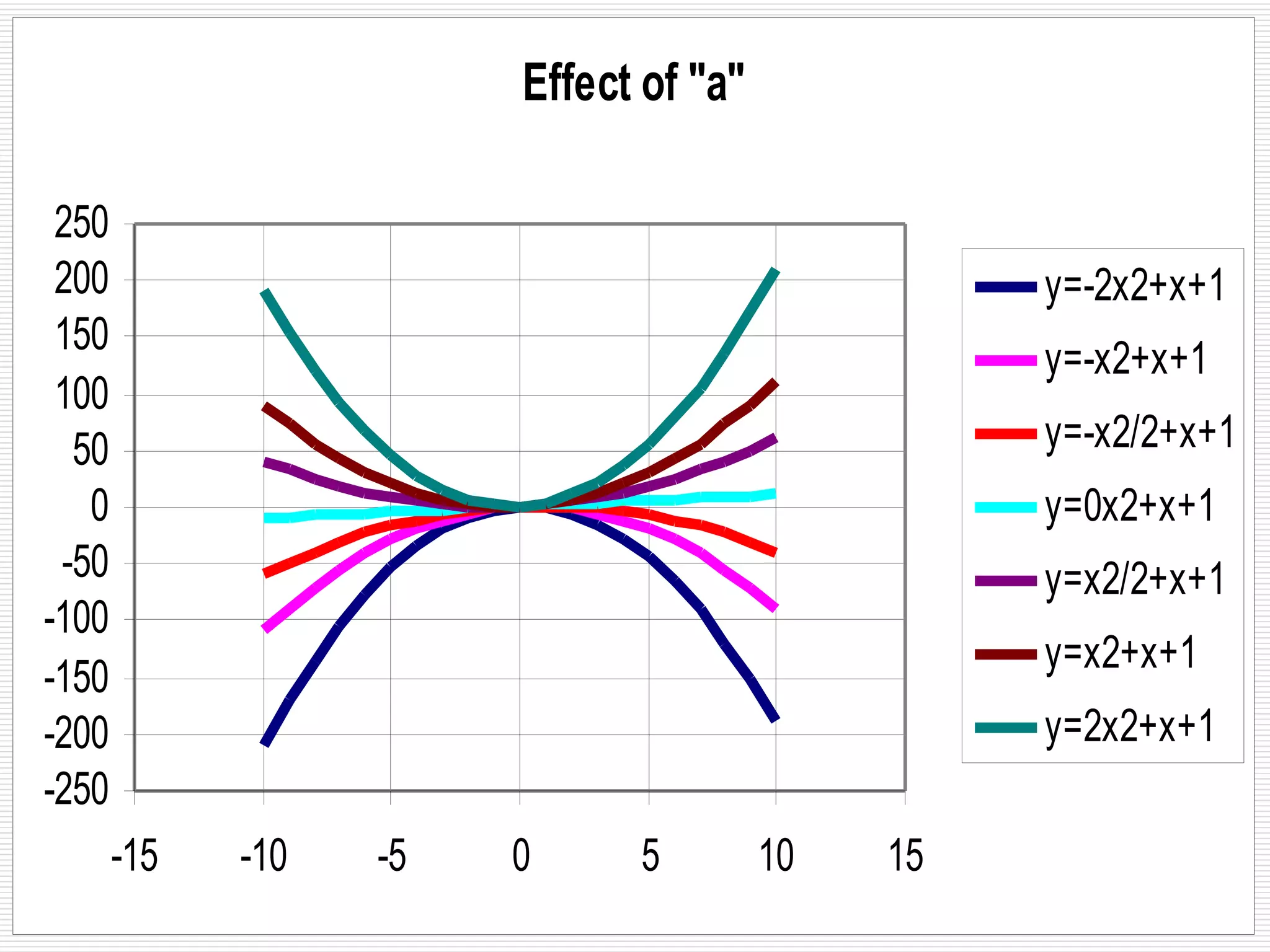
This document provides an overview of key physics concepts and mathematical tools. It covers units of measurement in the SI system, vector notation and operations like addition/subtraction, trigonometry, and dimensional analysis. Example problems demonstrate various concepts like finding components of vectors and adding multiple vectors. The document concludes with additional mathematical rules and functions important for physics problems.








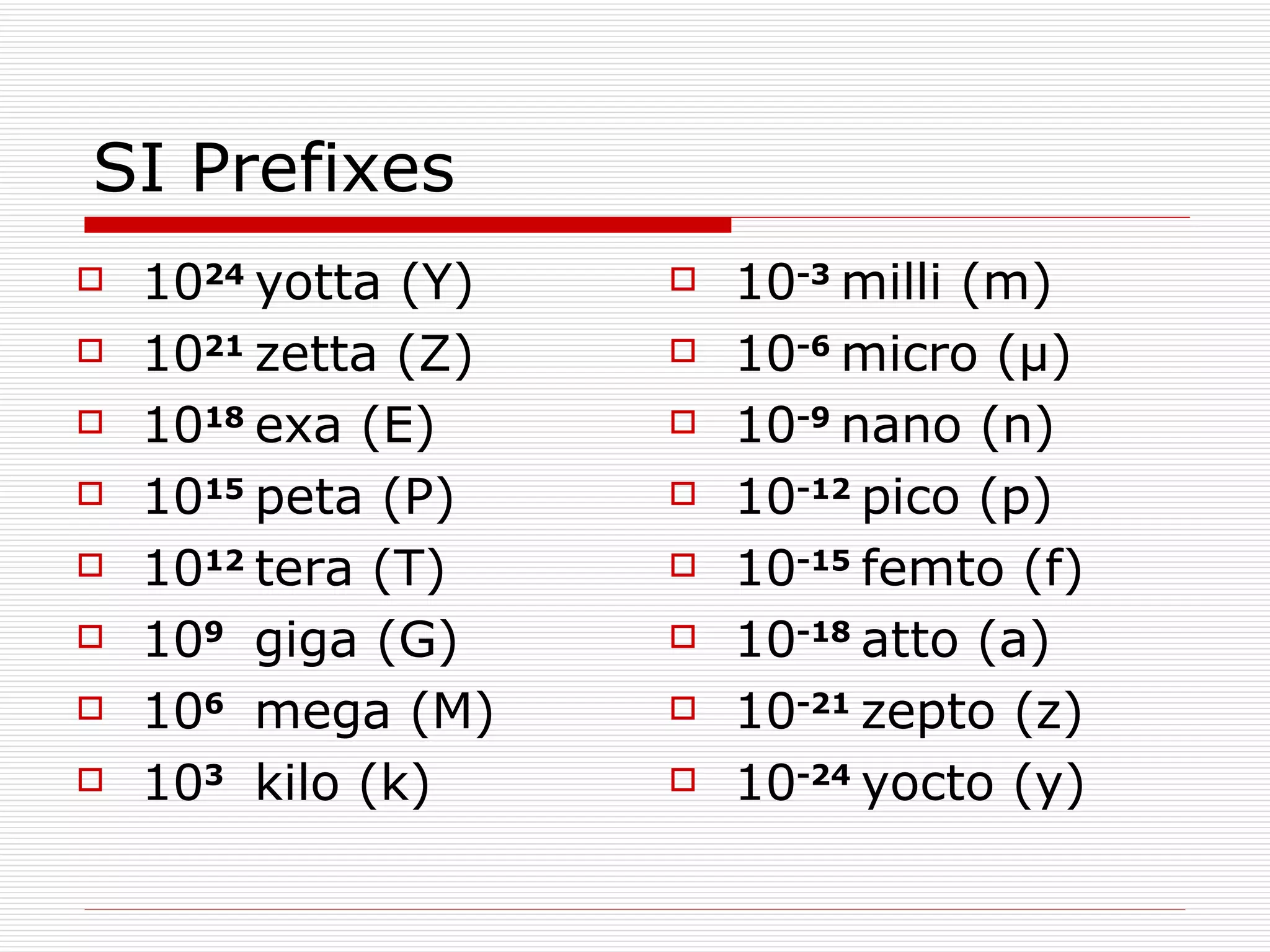







![Example DIMENSIONAL ANALYSIS [L] = length [M] = mass [T] = time Is the following equation dimensionally correct?](https://image.slidesharecdn.com/chapter1introductionandmathconceptsonline-110802100716-phpapp02/75/Ch-1-Introduction-and-Math-Concepts-17-2048.jpg)