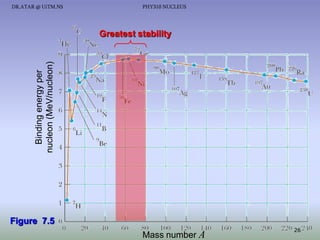
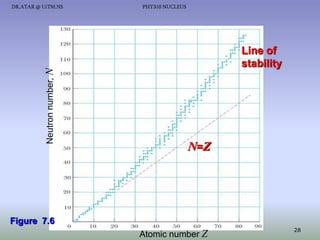
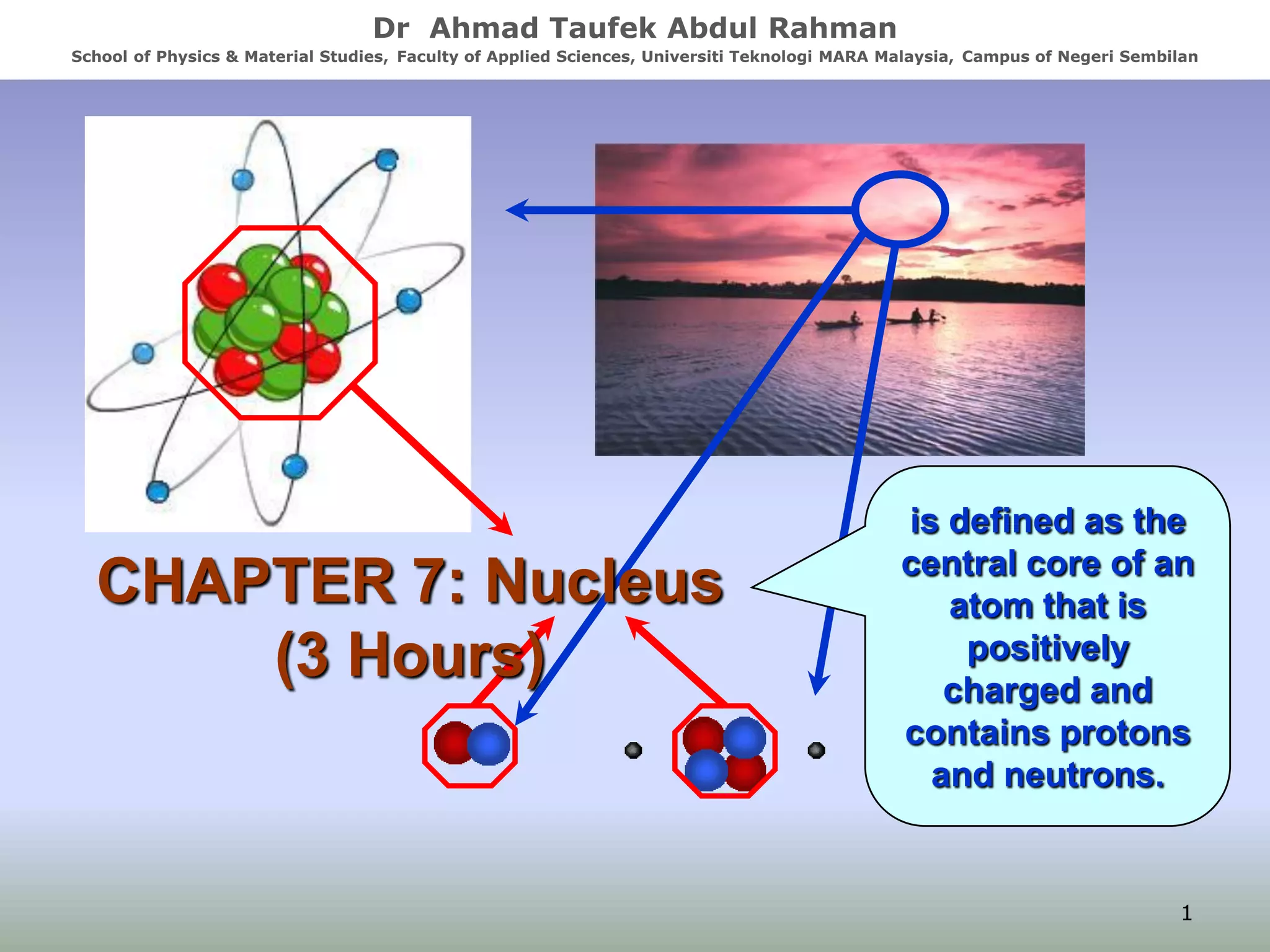
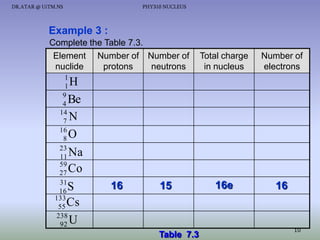
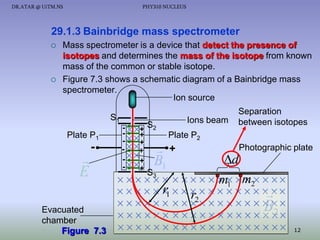
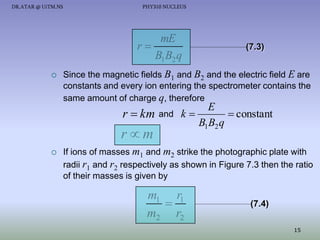
The document discusses properties of the nucleus, including: - The nucleus contains positively charged protons and uncharged neutrons. - Isotopes of an element have the same number of protons but different numbers of neutrons. - A mass spectrometer can be used to separate isotopes based on their different masses, producing a characteristic pattern on a photographic plate.

1. Dr Ahmad Taufek Abdul Rahman
School of Physics & Material Studies, Faculty of Applied Sciences, Universiti Teknologi MARA Malaysia, Campus of Negeri Sembilan
CHAPTER 7: Nucleus
(3 Hours)
is defined as the
central core of an
atom that is
positively
charged and
contains protons
and neutrons.
1

2. DR.ATAR @ UiTM.NS
PHY310 NUCLEUS
Learning Outcome:
7.1 Properties of nucleus (1 hour)
At the end of this chapter, students should be able to:

State the properties of proton and neutron.

Define
 proton number
 nucleon number
 isotopes

Use
A
to represent a nucleus.
ZX

Explain the working principle and the use of mass
spectrometer to identify isotopes.
2

3. DR.ATAR @ UiTM.NS
PHY310 NUCLEUS
7.1 Properties of nucleus
7.1.1 Nuclear structure

A nucleus of an atom is made up of protons and neutrons that
known as nucleons (is defined as the particles found inside
the nucleus) as shown in Figure 7.1.
Proton
Neutron
Electron
Figure 7.1
3

4. DR.ATAR @ UiTM.NS

PHY310 NUCLEUS
Proton and neutron are characterised by the following properties
in Table 7.1.
Proton (p)
Charge (C)
Mass (kg)
Neutron (n)
+e
0
(uncharged )
(1.60 10
19
)
1.672  10 27
1.675  10
27
Table 7.1

For a neutral atom,
 The number of protons inside the nucleus
= the number of electrons orbiting the nucleus
 This is because the magnitude of an electron charge
equals to the magnitude of a proton charge but opposite
in sign.
4

5. DR.ATAR @ UiTM.NS

PHY310 NUCLEUS
Nuclei are characterised by the number and type of nucleons
they contain as shown in Table 7.2.
Number
Symbol
Definition
Atomic number
Z
The number of protons in a nucleus
Neutron number
N
The number of neutrons in a nucleus
Mass (nucleon)
number
A
The number of nucleons in a nucleus
Table 7.2
Relationship :


(7.1)
Any nucleus of elements in the periodic table called a nuclide is
characterised by its atomic number Z and its mass number A.
The nuclide of an element can be represented as in the Figure
7.2.
5

6. DR.ATAR @ UiTM.NS
PHY310 NUCLEUS
Mass number
Element X
Atomic number

Figure 7.2
The number of protons Z is not necessary equal to the number
of neutrons N.
e.g. : 24 Mg
12
;
32
16
Z  12
N  A  Z  12
S ; 195 Pt
78
6

7. DR.ATAR @ UiTM.NS

PHY310 NUCLEUS
Since a nucleus can be modeled as tightly packed sphere
where each sphere is a nucleon, thus the average radius of
the nucleus is given by
R  R0 A
1
3
(7.2)
R : average radius of nucleus
15
R0 : constant  1.2 10 m OR 1.2 fm
A : mass (nucleon) number
where
femtometre (fermi)
1 fm  11015 m
7

8. DR.ATAR @ UiTM.NS
PHY310 NUCLEUS
Example 1 :
Based on the periodic table of element, Write down the symbol of
nuclide for following cases:
a. Z =20 ; A =40
b. Z =17 ; A =35
c. 50 nucleons ; 24 electrons
d. 106 nucleons ; 48 protons
e. 214 nucleons ; 131 protons
Solution :
a. Given Z =20 ; A =40
A
Z
X
40
20
Ca
c. Given A=50 and Z=number of protons = number of electrons =24
A
Z
X
50
24
Cr
8

9. DR.ATAR @ UiTM.NS
PHY310 NUCLEUS
Example 2 :
What is meant by the following symbols?
1
0
1
1
0
1
n; p ; e
State the mass number and sign of the charge for each entity
above.
Solution :
1
0
n
Neutron ; A=1
Charge : neutral (uncharged)
1
1
p
Proton ; A=1
Charge : positively charged
0
1
e
Electron ; A=0
Charge : negatively charged
9

10. DR.ATAR @ UiTM.NS
PHY310 NUCLEUS
Example 3 :
Complete the Table 7.3.
Element Number of Number of
nuclide
protons
neutrons
1
1
9
4
14
7
16
8
23
11
59
27
31
16
133
55
238
92
H
Be
N
O
Na
Co
S
Cs
U
16
15
Table 7.3
Total charge
in nucleus
Number of
electrons
16e
16
10

11. DR.ATAR @ UiTM.NS
PHY310 NUCLEUS
7.1.2 Isotope


is defined as the nuclides/elements/atoms that have the
same atomic number Z but different in mass number A.
From the definition of isotope, thus the number of protons or
electrons are equal but different in the number of neutrons
N for two isotopes from the same element.
For example :
 Hydrogen isotopes:
1
1
H : Z=1, A=1, N=0
2
: Z=1, A=2, N=1
1H
proton(1 p)
1
deuterium( 2 D)
1
tritium (31T)
: Z=1, A=3, N=2
H
not equal
Oxygen isotopes: equal
3
1

16
8
17
8
18
8
O : Z=8, A=16, N=8
O : Z=8, A=17, N=9
O : Z=8, A=18, N=10
equal
not equal
11

12. DR.ATAR @ UiTM.NS
PHY310 NUCLEUS
29.1.3 Bainbridge mass spectrometer


Mass spectrometer is a device that detect the presence of
isotopes and determines the mass of the isotope from known
mass of the common or stable isotope.
Figure 7.3 shows a schematic diagram of a Bainbridge mass
spectrometer.
Ion source
S1
Plate P1

E
-
Evacuated
chamber
Figure 7.3
- + S2
-
Ions beam
Separation
between isotopes
Plate P2
+
+
+  +
Photographic plate
+ B
d
+ 1
S3
             m2  
m1 
r
     1           
r2
                 
B
  2
                  12
-

13. DR.ATAR @ UiTM.NS
PHY310 NUCLEUS
Working principle
 Ions from an ion source such as a discharge tube are narrowed
to a fine beam by the slits S1 and S2.
 The ions beam then passes through a velocity selector (plates
P1 and P2) which uses a uniform magnetic field B1 and a uniform
electric field E that are perpendicular to each other.

The beam with selected velocity v passes through the velocity
selector without deflection and emerge from the slit S3. Hence,
the force on an ion due to the magnetic field B1 and the electric
field E are equal in magnitude but opposite in direction (Figure
7.4).
Plate P1
Plate P2
Figure 7.4



 


FE  


  
v



 B
F


Using Fleming’s
left hand rule.
13

14. DR.ATAR @ UiTM.NS
PHY310 NUCLEUS
Thus the selected velocity is
FB  FE
qvB1 sin 90  qE
E
v
B1

The ions beam emerging from the slit S3 enter an evacuated
chamber of uniform magnetic field B2 which is perpendicular to
the selected velocity v. The force due to the magnetic field B2
causes an ion to move in a semicircle path of radius r given by
FB  Fc
mv 2
qvB2 sin 90  
r
mv
r
B2 q
and
E
v
B1
14

15. DR.ATAR @ UiTM.NS
PHY310 NUCLEUS
mE
r
B1 B2 q

(7.3)
Since the magnetic fields B1 and B2 and the electric field E are
constants and every ion entering the spectrometer contains the
same amount of charge q, therefore
E
 constant
r  km and k 
B1B2 q
rm

If ions of masses m1 and m2 strike the photographic plate with
radii r1 and r2 respectively as shown in Figure 7.3 then the ratio
of their masses is given by
m1 r1

m2 r2
(7.4)
15

16. DR.ATAR @ UiTM.NS
PHY310 NUCLEUS
Example 4 :
A beam of singly charged ions of isotopes Ne-20 and Ne-22 travels
straight through the velocity selector of a Bainbridge mass
spectrometer. The mutually perpendicular electric and magnetic
fields in the velocity selector are 0.4 MV m1 and 0.7 T respectively.
These ions then enter a chamber of uniform magnetic flux density
1.0 T. Calculate
a. the selected velocity of the ions,
b. the separation between two isotopes on the photographic plate.
(Given the mass of Ne-20 = 3.32  1026 kg; mass of Ne-22 =
3.65  1026 kg and charge of the beam is 1.60  1019 C)
Solution : E  0.4  10 6 V m 1 ; B1  0.7 T; B2  1.0 T
a. The selected velocity of the ions is
E
v
B1
0.4  10 6
v
0.7
v  5.71  10 5 m s 1
16

17. DR.ATAR @ UiTM.NS
PHY310 NUCLEUS
Solution : E  0.4  10 6 V m 1 ; B  0.7 T; B  1.0 T
1
2
b. The radius of the circular path made by isotope Ne-20 is
m1 E
r1 
B1 B2 q
3.32 10 0.4 10 
r 
0.7 1.01.60  10 
26
6
19
1
 0.119 m
and the radius of the circular path made by isotope Ne-22 is
3.65 10 0.4 10 

0.7 1.01.60  10 
26
r2
6
19
 0.130 m
Therefore the separation between the isotope of Ne is given by
d  d 2  d1
Figure 7.3
d  2r2  2r1
 2r2  r1 
 20.130  0.119 
d  2.2  10 2 m
17

18. DR.ATAR @ UiTM.NS
PHY310 NUCLEUS
Learning Outcome:
7.2 Binding energy and mass defect (2 hours)
At the end of this chapter, students should be able to:

Define mass defect and binding energy.

Use formulae
E  mc 2

Identify the average value of binding energy per
nucleon of stable nuclei from the graph of binding
energy per nucleon against nucleon number.
18

19. DR.ATAR @ UiTM.NS
PHY310 NUCLEUS
7.2 Binding energy and mass defect
7.2.1 Einstein mass-energy relation


From the theory of relativity leads to the idea that mass is a
form of energy.
Mass and energy can be related by the following relation:
E  mc 2
where
(7.5)
E : amount of energy
m : rest mass
c : speed of light in vacuum (3.00 108 m s 1 )
e.g. The energy for 1 kg of substance is
E  mc 2
 (1)(3.00 108 ) 2
E  9.00  1016 J
19

20. DR.ATAR @ UiTM.NS
PHY310 NUCLEUS
Unit conversion of mass and energy

The electron-volt (eV)
 is a unit of energy.
 is defined as the kinetic energy gained by an electron in
being accelerated by a potential difference (voltage) of 1
volt.
19
1 eV  1.60 10 J
1 MeV  106 eV  1.60 1013 J

The atomic mass unit (u)
 is a unit of mass.
1
 is defined as exactly
the mass of a neutral carbon-12
12
atom.
mass of 12C
6
1u 
12
1 u  1.66 1027 kg
20

21. DR.ATAR @ UiTM.NS
PHY310 NUCLEUS

1 atomic mass unit (u) can be converted into the unit of
energy by using the mass-energy relation (eq. 7.5).
E  mc 2
 (1.66 10 27 )(3.00 108 ) 2
E  1.49  10 10 J

in joule,
1 u  1.49 1010 J

in eV/c2 or MeV/c2,
1.49  10 10
E
 931.5  10 6 eV/c 2
1.60  10 19
1 u  931.5 106 eV/ c 2
OR
1 u  931.5 MeV/ c 2
21

22. DR.ATAR @ UiTM.NS
PHY310 NUCLEUS
7.2.2 Mass defect

The mass of a nucleus (MA) is always less than the total mass
of its constituent nucleons (Zmp+Nmn) i.e.

M A  Zmp  Nmn
where


mp : mass of a proton
mn : mass of a neutron
Thus the difference in this mass is given by


m  Zm p  Nmn  M A


(7.6)
where m is called mass defect and is defined as the mass
difference between the total mass of the constituent
nucleons and the mass of a nucleus.
The reduction in mass arises because the act of combining
the nucleons to form the nucleus causes some of their mass
to be released as energy.
Any attempt to separate the nucleons would involve them
being given this same amount of energy. This energy is called
22
the binding energy of the nucleus.

23. DR.ATAR @ UiTM.NS
PHY310 NUCLEUS
7.2.3 Binding energy


The binding energy of a nucleus is defined as the energy
required to separate completely all the nucleons in the
nucleus.
The binding energy of the nucleus is equal to the energy
equivalent of the mass defect. Hence
Binding energy
in joule
EB  mc 2
Mass defect in kg
(7.7)
Speed of light in
vacuum
7.2.4 Nucleus stability


Since the nucleus is viewed as a closed packed of nucleons,
thus its stability depends only on the forces exist inside it.
The forces involve inside the nucleus are
 repulsive electrostatic (Coulomb) forces between
protons and
 attractive forces that bind all nucleons together in the
23
nucleus.

24. DR.ATAR @ UiTM.NS


PHY310 NUCLEUS
These attractive force is called nuclear force and is responsible
for nucleus stability.
The general properties of the nuclear force are summarized
as follow :
 The nuclear force is attractive and is the strongest force
in nature.
 It is a short range force . It means that a nucleon is
attracted only to its nearest neighbours in the nucleus.
 It does not depend on charge; neutrons as well as protons
are bound and the nuclear force is same for both.
e.g. proton-proton (p-p)
The magnitude of nuclear
neutron-neutron (n-n)
forces are same.
proton-neutron (p-n)

The nuclear force depends on the binding energy per
nucleon.
24

25. DR.ATAR @ UiTM.NS


PHY310 NUCLEUS
Note that a nucleus is stable if the nuclear force greater than
the Coulomb force and vice versa.
The binding energy per nucleon of a nucleus is a measure of
the nucleus stability where
Binding energy ( EB )
Binding energy per nucleon 
Nucleon number( A)
mc 2
Binding energy per nucleon 
A

(7.8)
Figure 7.5 shows a graph of the binding energy per nucleon as
a function of mass (nucleon) number A.
25

26. DR.ATAR @ UiTM.NS
PHY310 NUCLEUS
Binding energy per
nucleon (MeV/nucleon)
Greatest stability
Figure 7.5
Mass number A
26

27. DR.ATAR @ UiTM.NS

PHY310 NUCLEUS
From Figure 7.5,


For the nuclei with A between 50 and 80, the value of EB/A
ranges between 8.0 and 8.9 Mev/nucleon. The nuclei in
these range are very stable. The maximum value of the
curve occurs in the vicinity of nickel, which has the most
stable nucleus.

For A > 62, the values of EB/A decreases slowly, indicating
that the nucleons are on average less tightly bound.


The value of EB/A rises rapidly from 1 MeV/nucleon to 8
MeV/nucleon with increasing mass number A for light nuclei.
For heavy nuclei with A between 200 to 240, the binding
energy is between 7.5 and 8.0 MeV/nucleon. These nuclei
are unstable and radioactive.
Figure 7.6 shows a graph of neutron number N against atomic
number Z for a number of stable nuclei.
27

28. Neutron number, N
DR.ATAR @ UiTM.NS
PHY310 NUCLEUS
Line of
stability
N=Z
Figure 7.6
Atomic number Z
28

29. DR.ATAR @ UiTM.NS

PHY310 NUCLEUS
From Figure 7.6,
 The stable nuclei are represented by the blue dots, which lie
in a narrow range called the line of stability.

The dashed line corresponds to the condition N=Z.

The light stable nuclei contain an equal number of
protons and neutrons (N=Z) but in heavy stable nuclei
the number of neutrons always greater than the number
of protons (above Z =20) hence the line of stability
deviates upward from the line of N=Z.


This means as the number of protons increase, the
strength of repulsive coulomb force increases which
tends to break the nucleus apart.
As a result, more neutrons are needed to keep the
nucleus stable because neutrons experience only the
attractive nuclear force.
29

30. DR.ATAR @ UiTM.NS
PHY310 NUCLEUS
Example 5 :
Calculate the binding energy of an aluminum nucleus

27
13 Al
 in MeV.
(Given mass of neutron, mn=1.00867 u ; mass of proton,
mp=1.00782 u ; speed of light in vacuum, c=3.00108 m s1 and
atomic mass of aluminum, MAl=26.98154 u)
Solution :
27
13 Al
Z  13 and N  27 13
N  14
The mass defect of the aluminum nucleus is
m  Zmp  Nmn   M Al
 13 1.00782  14 1.00867  26.98154
m  0.2415 u
30

31. DR.ATAR @ UiTM.NS
PHY310 NUCLEUS
Solution :
The binding energy of the aluminum nucleus can be calculated by
using two method.
2
1st method:
1 u  1.66 1027 kg
E  m c
B


in kg

m  0.2415 1.66 1027
28
 4.0089 10 kg

 28


EB  4.0089 10 3.00 10
EB  3.608 1011 J

8 2
Thus the binding energy in MeV is
11
3.608 10
EB 
1.60 10 13
EB  226 MeV
1 MeV  1.60 1013 J
31

32. DR.ATAR @ UiTM.NS
Solution :
2nd method:
PHY310 NUCLEUS
EB  mc 2
1 u  931.5 MeV/c 2
in u
  931.5 MeV/ c 2  2
 c
 m


1u

 

 931.5 MeV/ c 2  2
 c
 0.2415 u 


1u



EB  225 MeV
32

33. DR.ATAR @ UiTM.NS
PHY310 NUCLEUS
Example 6 :
Calculate the binding energy per nucleon of a boron nucleus
in J/nucleon.
 B
10
5
(Given mass of neutron, mn=1.00867 u ; mass of proton,
mp=1.00782 u ; speed of light in vacuum, c=3.00108 m s1 and
atomic mass of boron, MB=10.01294 u)
Solution :
10
5
B
Z 5
and
N  10  5
N 5
The mass defect of the boron nucleus is
m  Zmp  Nmn   M B
 5 1.00782  5 1.00867 10.01294
m  0.06951 u
33

34. DR.ATAR @ UiTM.NS
PHY310 NUCLEUS
Solution :
The binding energy of the boron nucleus is given by
EB  mc 2

 0.06951 1.66 10
 27
3.00 10 
8 2
EB  1.04 1011 J
Hence the binding energy per nucleon is
EB 1.04 1011

A
10
EB
 1.04 10 12 J/nucleon
A
34

35. DR.ATAR @ UiTM.NS
PHY310 NUCLEUS
Example 7 :


Why is the uranium-238 nucleus 238 U less stable than carbon-12
92
12
nucleus
? Give an explanation by referring to the repulsive
6C
coulomb force and the binding energy per nucleon.
 
(Given mass of neutron, mn=1.00867 u ; mass of proton,
mp=1.00782 u ; speed of light in vacuum, c=3.00108 m s1; atomic
mass of carbon-12, MC=12.00000 u and atomic mass of uranium238, MU=238.05079 u )
Solution :
From the aspect of repulsive coulomb force :

Uranium-238 nucleus has 92 protons but the carbon-12
nucleus has only 6 protons.

Therefore the coulomb force inside uranium-238 nucleus
is  92  or 15.3 times the coulomb force inside carbon-12
 
 6 
nucleus.
35

36. DR.ATAR @ UiTM.NS
PHY310 NUCLEUS
Solution :
From the aspect of binding energy per nucleon:
12
Z  6 and N  6

Carbon-12 : C
6
The mass defect :
m  Zmp  Nmn   M C
 6 1.00782  6 1.00867 12.00000
m  0.09894 u
The binding energy per nucleon:
mc
 EB 
  
A
 A C
 931.5 MeV/ c 2  2
c
0.09894 u 


1u



12
 EB 
   7.68 MeV/nucleo n
36
 A C
2

37. DR.ATAR @ UiTM.NS
PHY310 NUCLEUS

238
Uranium-238 :
92 U
The mass defect :
Z  92 and N  146
m  92 1.00782  146 1.00867  238.05079
m  1.93447 u
The binding energy per nucleon:
 931.5 MeV/ c 2  2
c
1.93447 u 


1u
 EB 



 
238
 A U
 EB 
   7.57 MeV/nucleo n
 A U
Since the binding energy of uranium-238 nucleus less than the
binding energy of carbon-12 and the coulomb force inside uranium238 nucleus greater than the coulomb force inside carbon-12
nucleus therefore uranium-238 nucleus less stable than carbon-12
nucleus.
37

38. DR.ATAR @ UiTM.NS
PHY310 NUCLEUS
Exercise 7.1 :
Given c =3.00108 m s1, mn=1.00867 u, mp=1.00782 u
1.
Calculate the binding energy in joule of a deuterium nucleus.
The mass of a deuterium nucleus is 3.34428  1027 kg.
ANS. : 2.781013 J
20
2. The mass of neon-20 nucleus 10 Ne is 19.99244 u. Calculate
the binding energy per nucleon of neon-20 nucleus in MeV
per nucleon.
ANS. : 8.03 MeV/nucleon
3. Determine the energy required to remove one neutron from an
oxygen-16 16 O . The atomic mass for oxygen-16 is
8
15.994915 u


 
(Physics, 3rd edition, James S. Walker, Q39, p.1108)
ANS. : 15.7 MeV
38

39. DR.ATAR @ UiTM.NS
PHY310 NUCLEUS
Next Chapter…
CHAPTER 8 :
RADIOACTIVITY
39