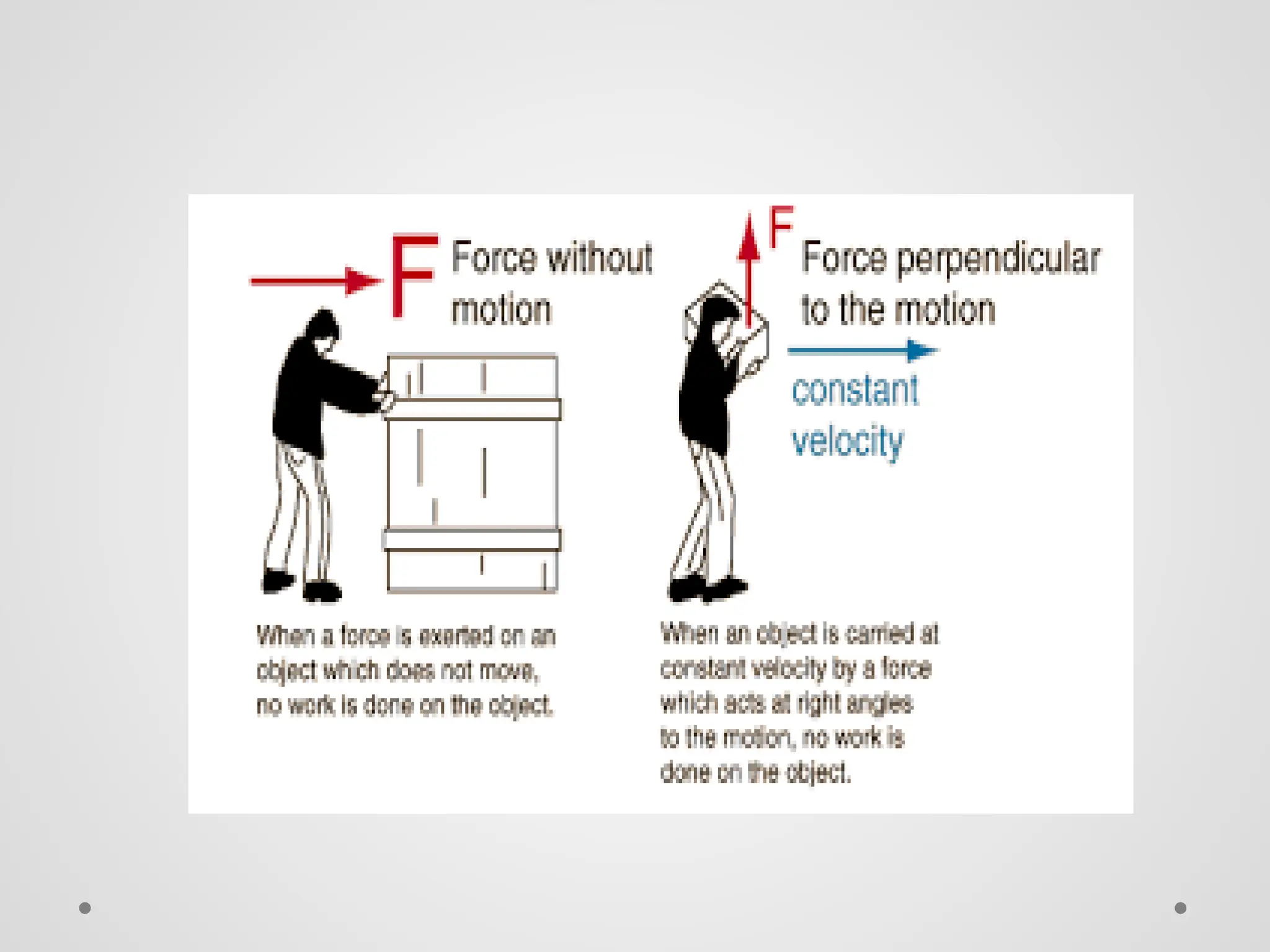
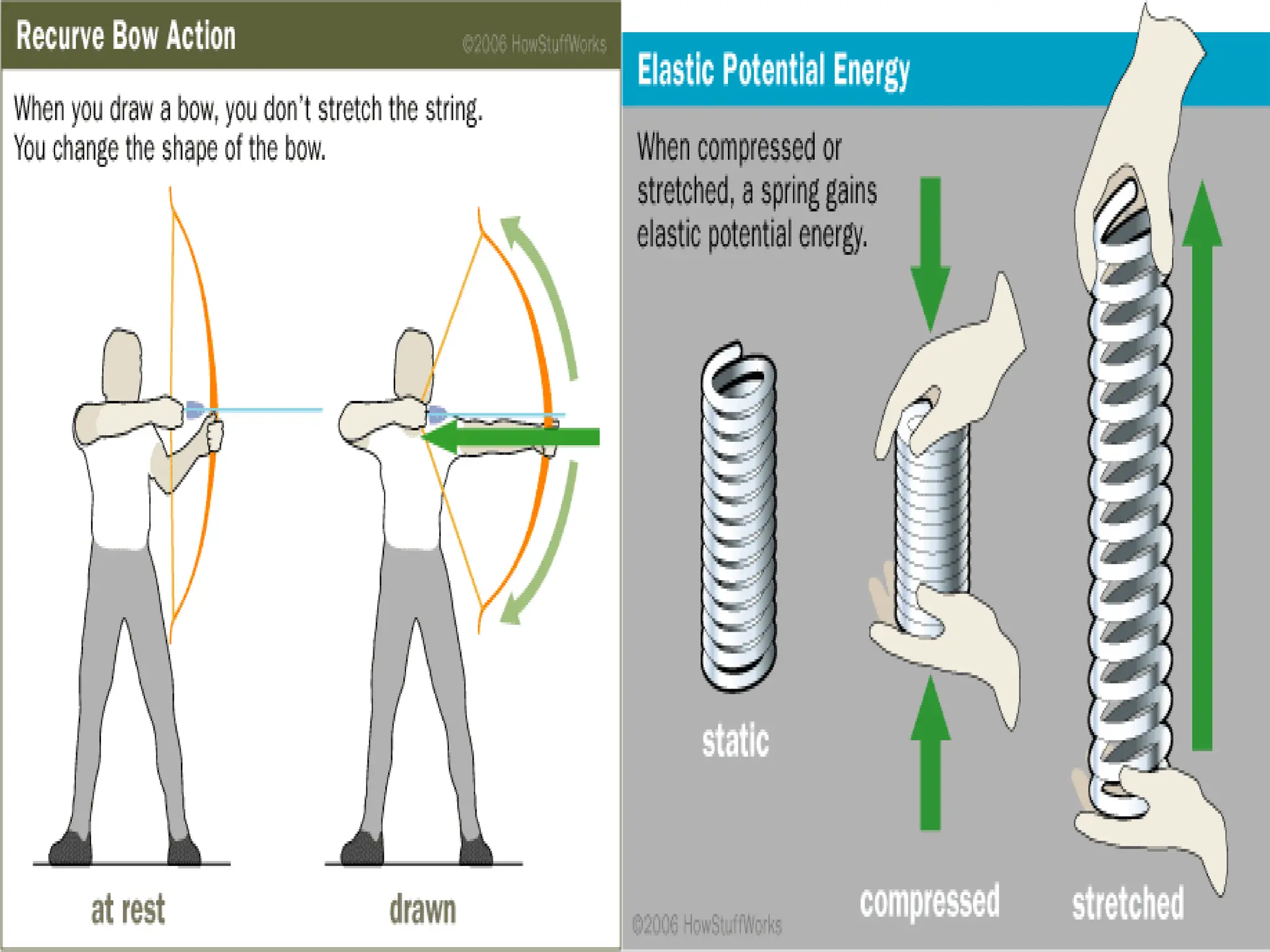
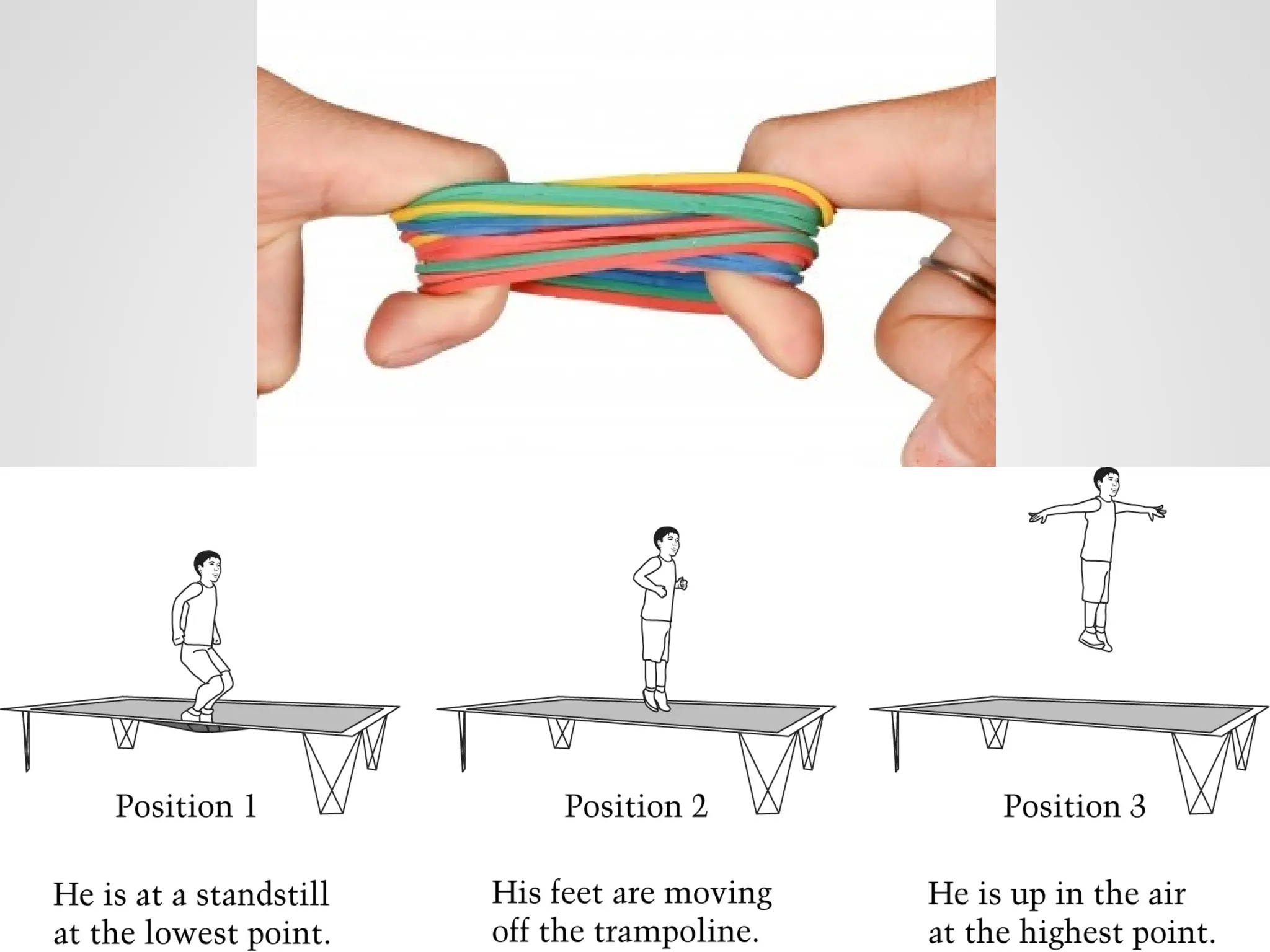
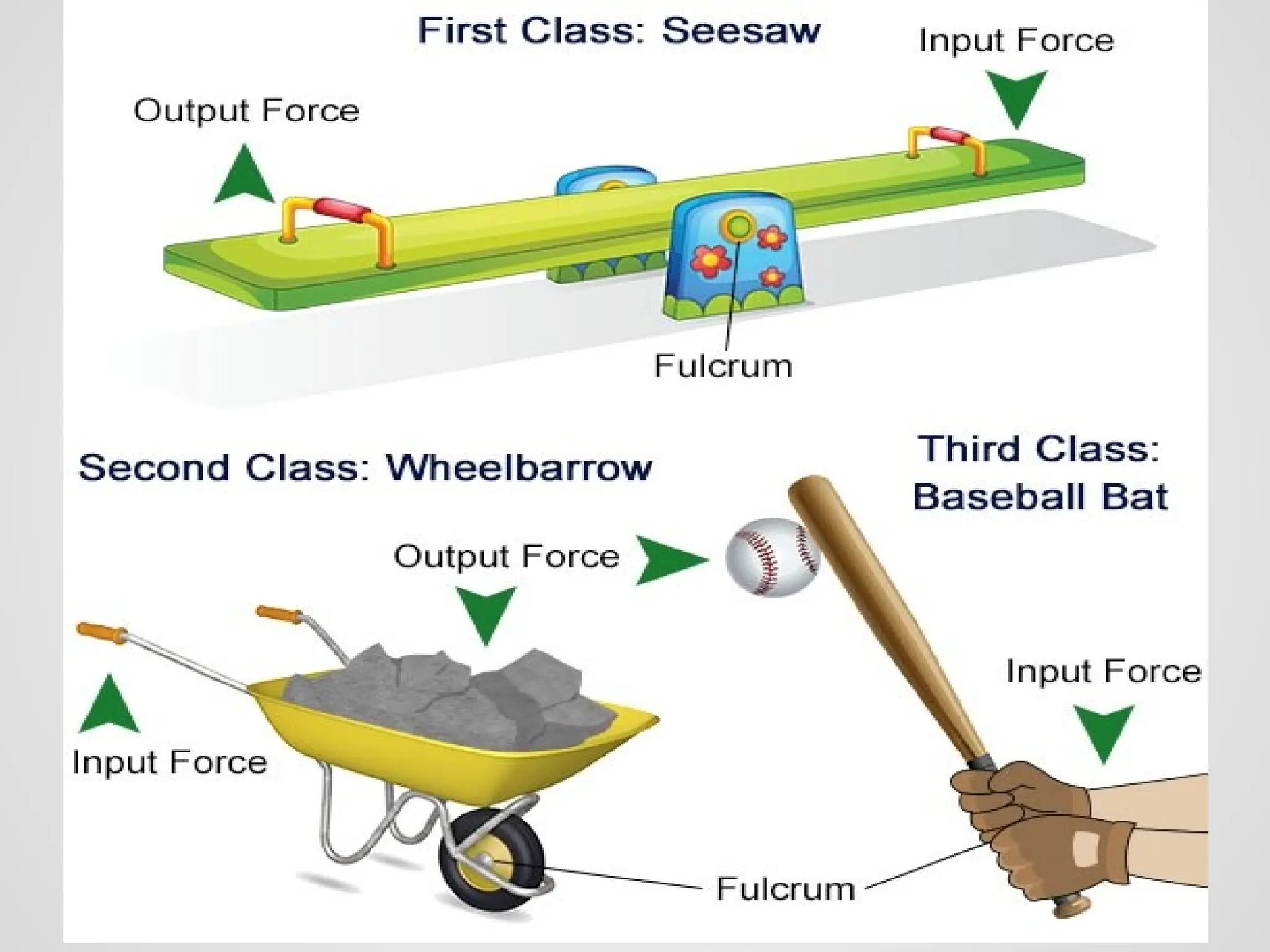
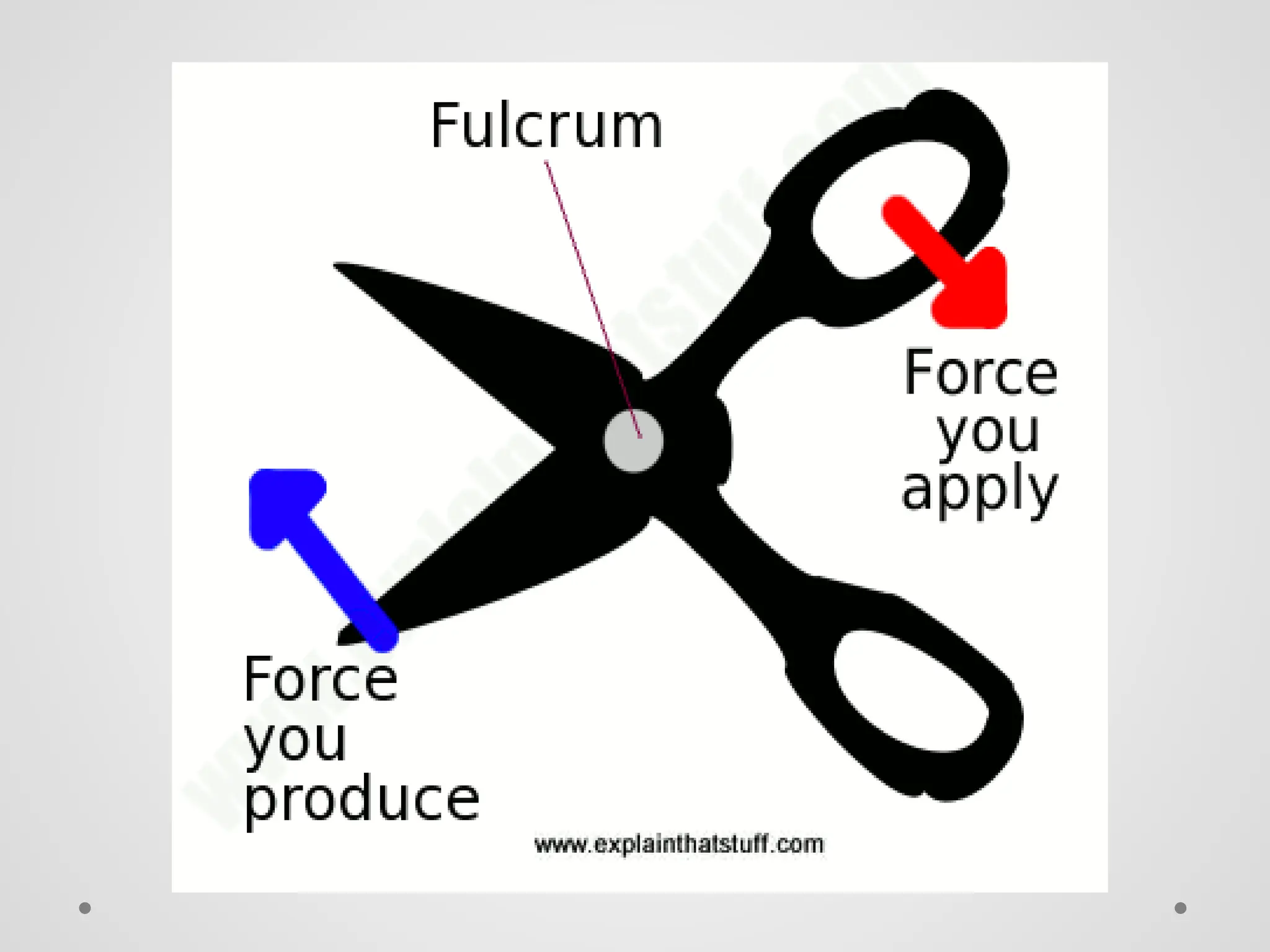
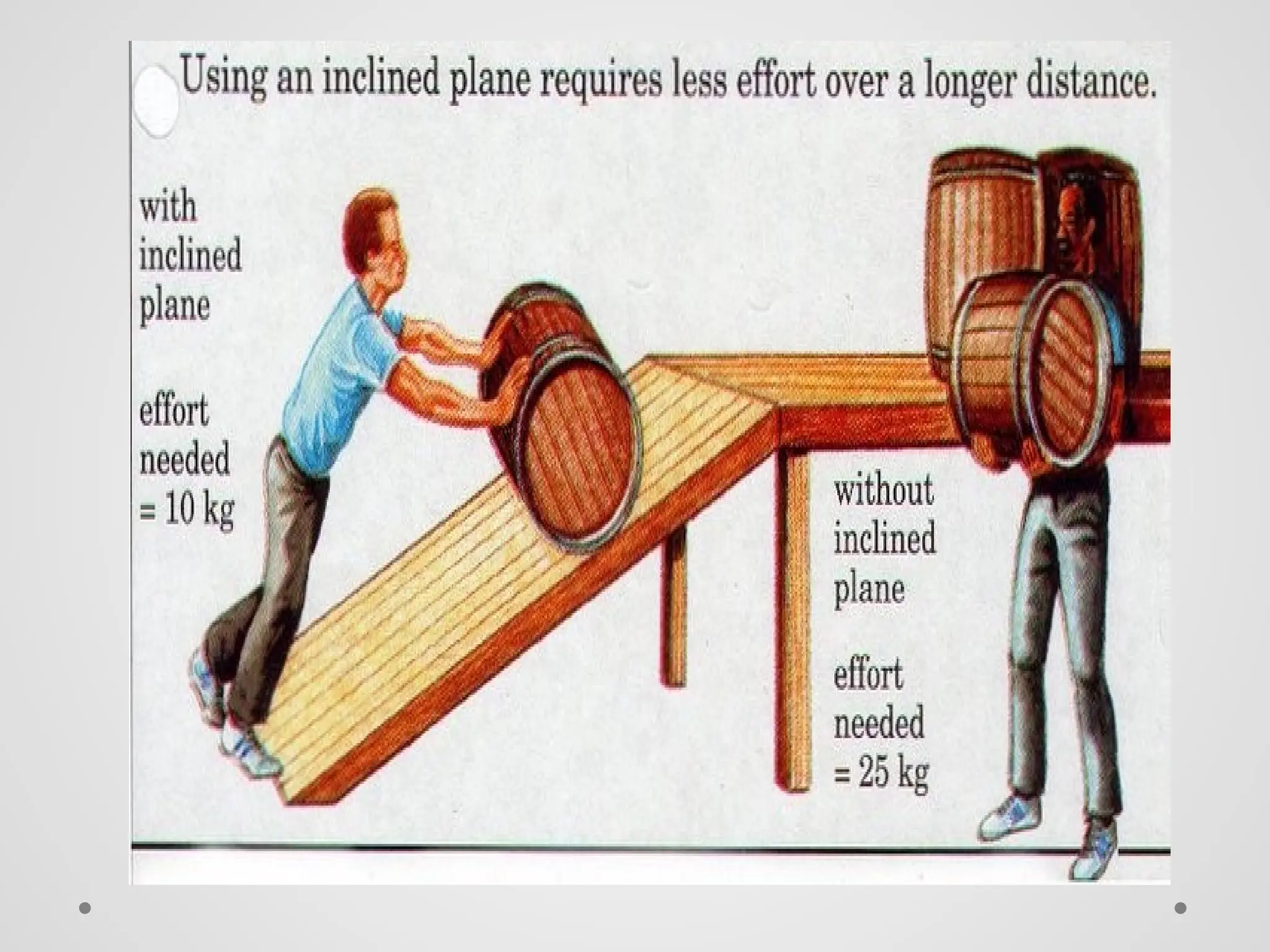
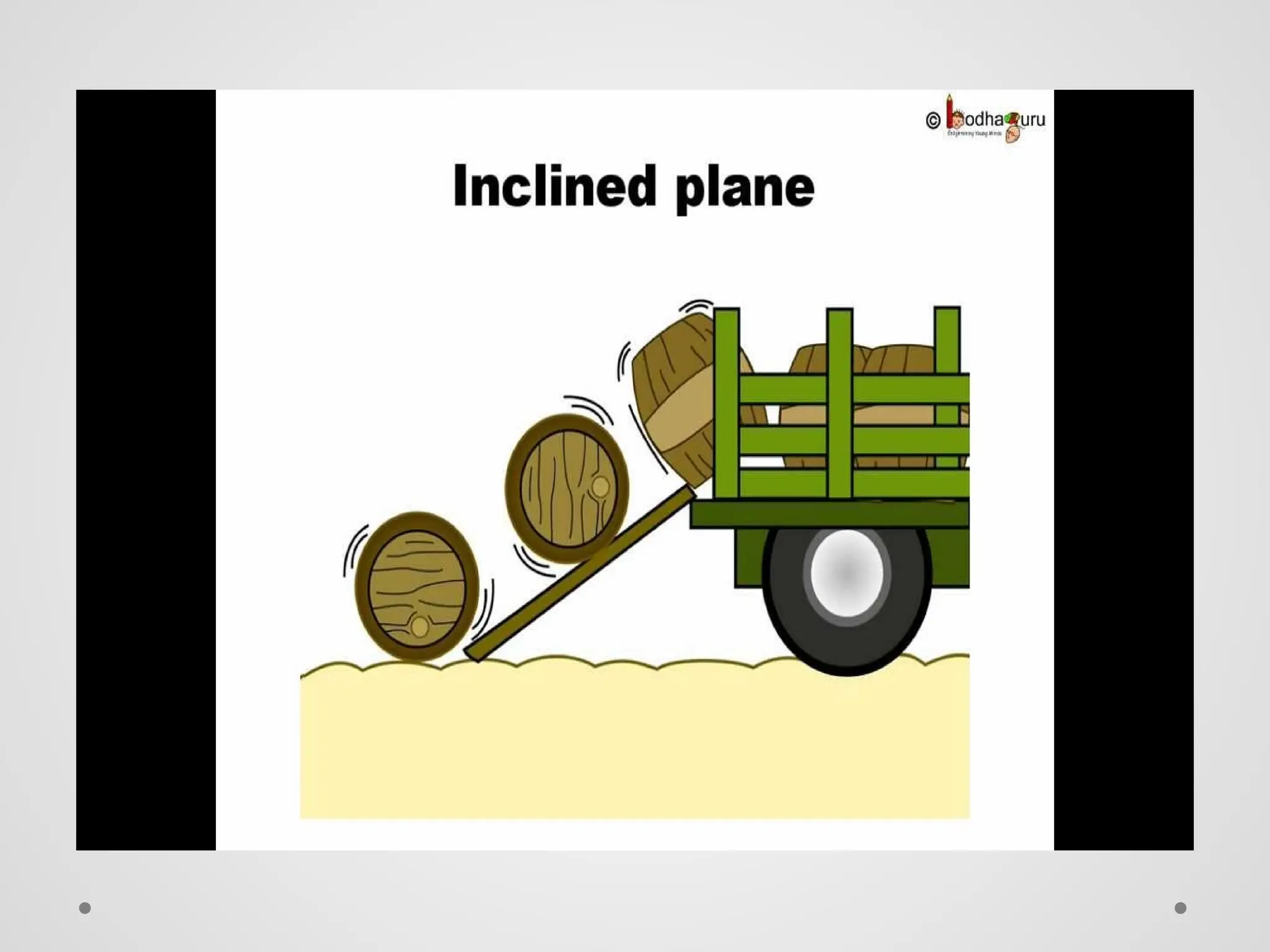
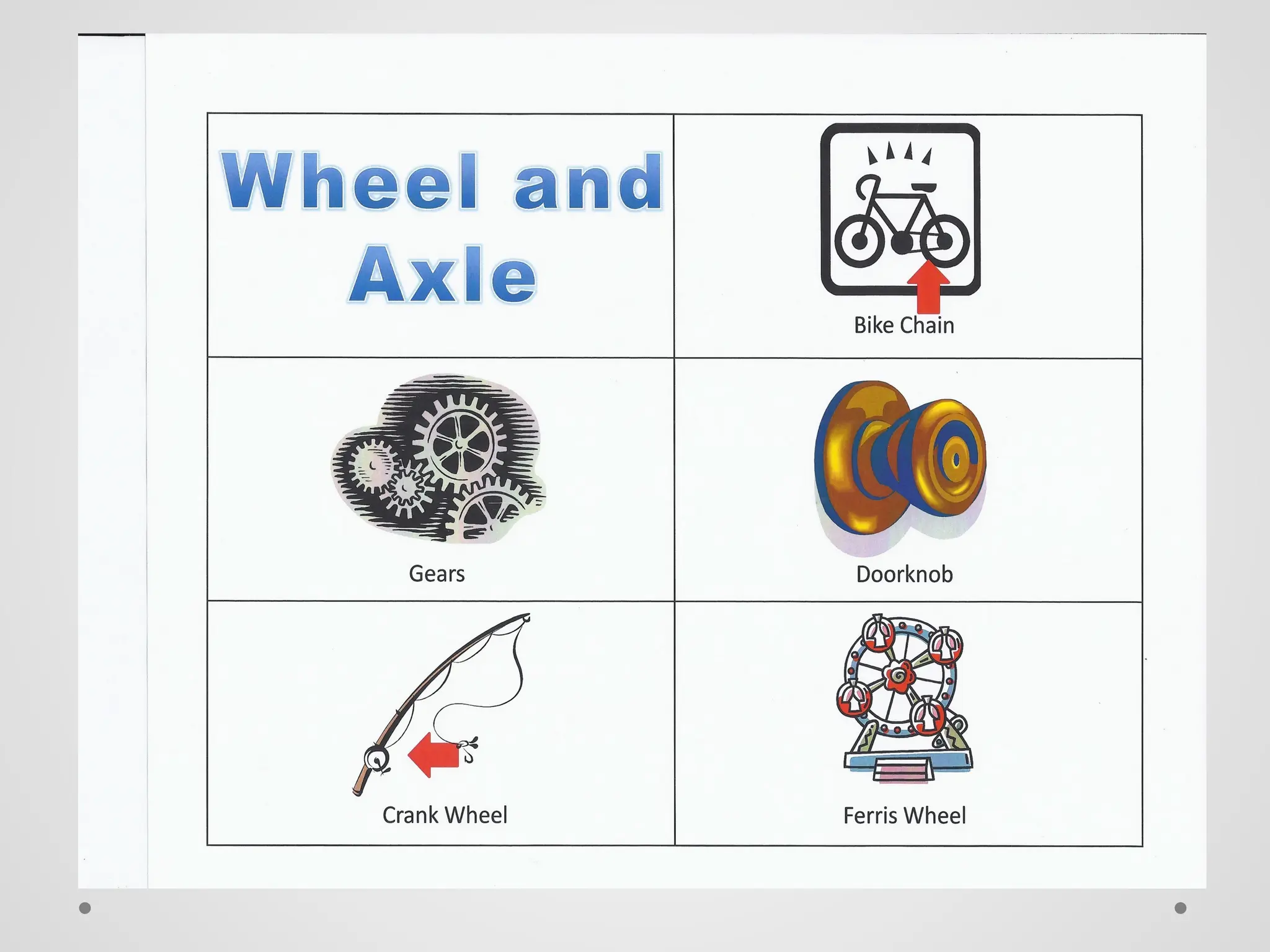
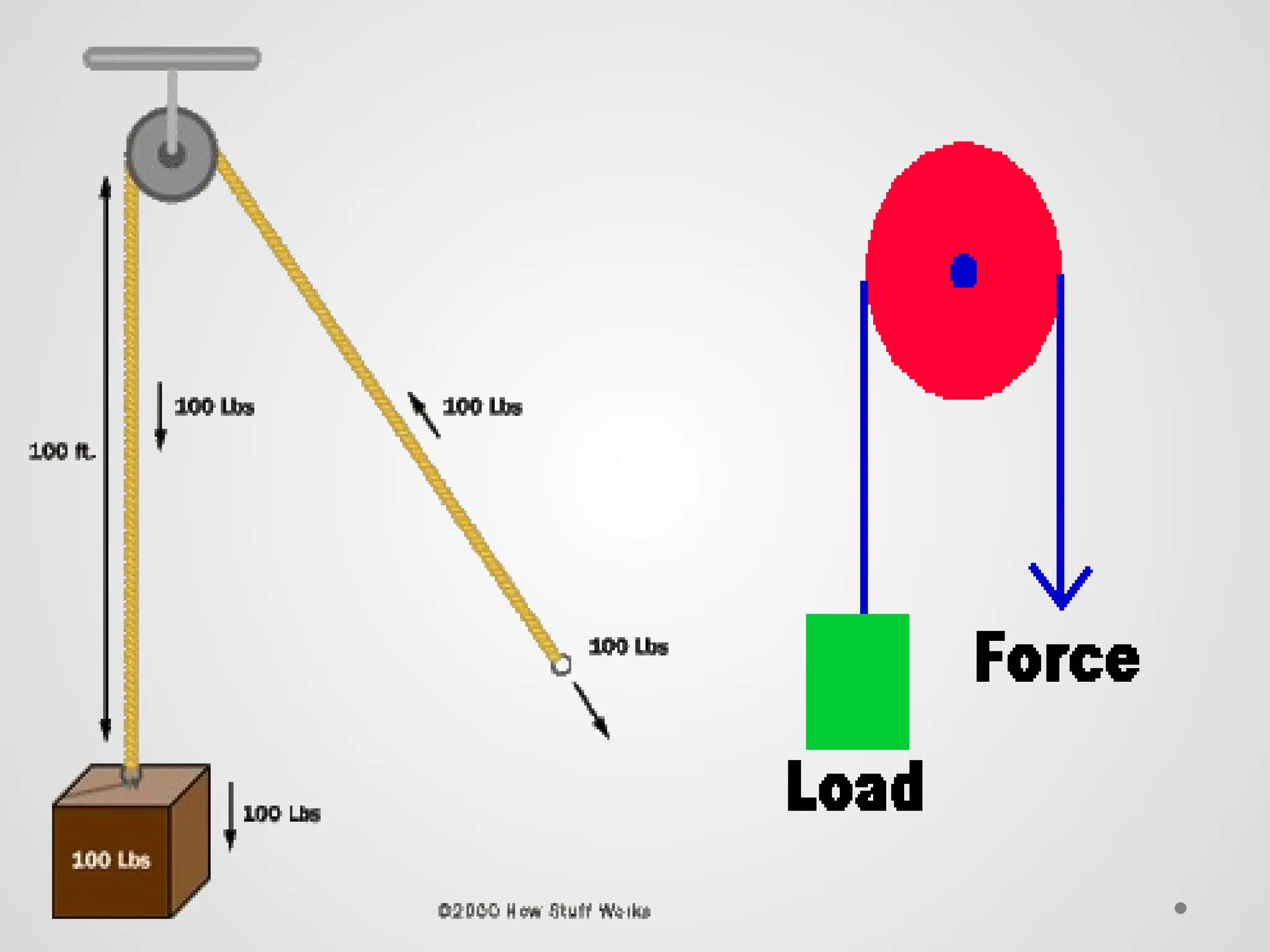
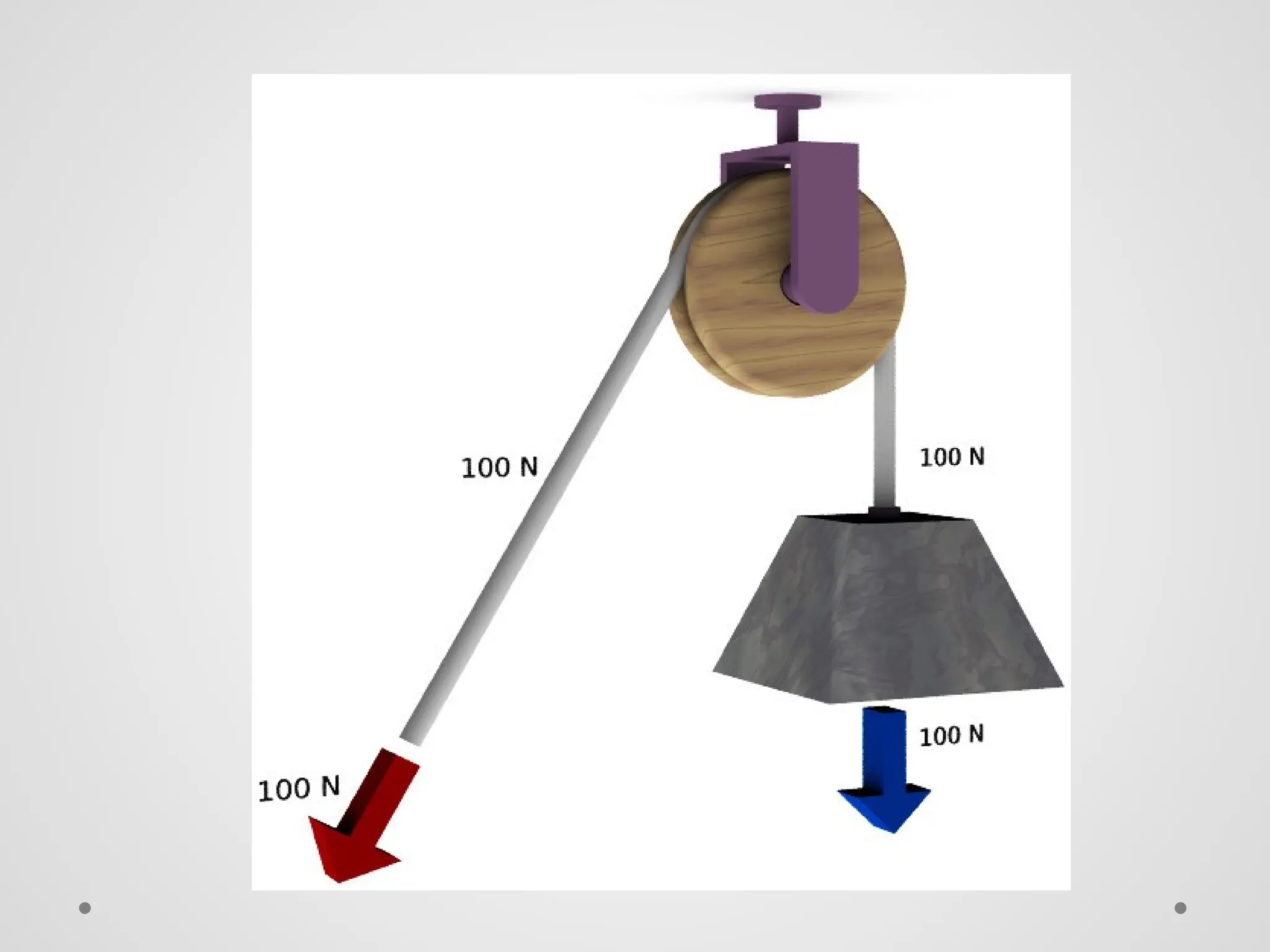
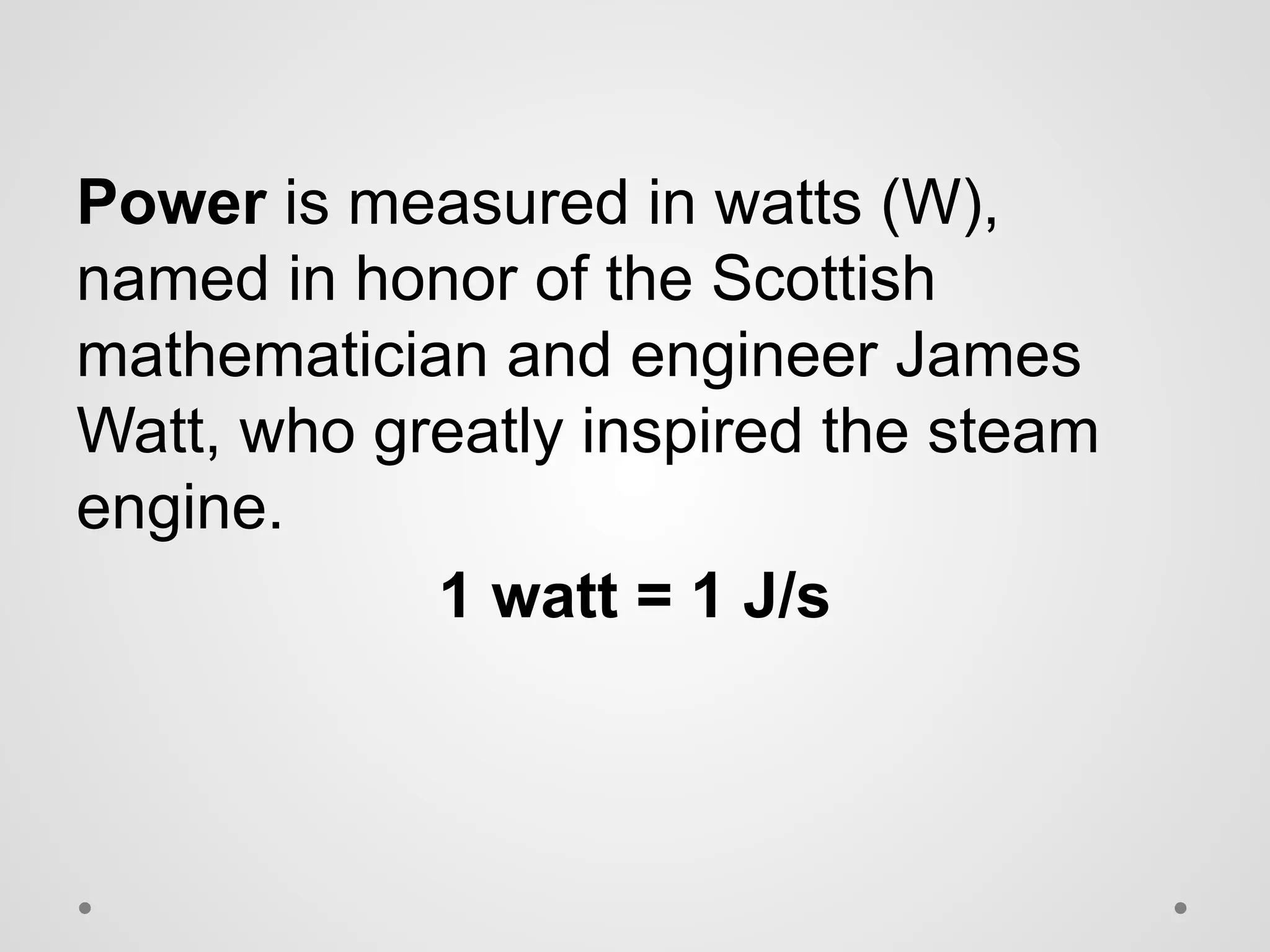El trabajo se define como la fuerza ejercida sobre un objeto multiplicada por la distancia que se mueve en la dirección de la fuerza, y se mide en julios. La energía se manifiesta como la capacidad de realizar trabajo, y existe en diversas formas como energía química, eléctrica, nuclear y mecánica, que se dividen en energía potencial y cinética. La potencia se define como la tasa de realización de trabajo y se mide en vatios, siendo la relación entre trabajo y tiempo.

1. Work, Energy and
Power

2. WORK

3. What is Work?
• The term work was introduce in 1826 by
the French mathematician Gaspard
Gustave Coriolis as " weight lifted
through a height" which is based on the
used of early steam engines to lift buckets
of water out of flooded ore mines.

4. • Work is defined as the force (F)
exerted in an object times the
distance (x) moved in the direction of
the force.
• The work done by the force is equal
to the product of the force and the
displacement.
W= Fx

5. For work to be done, three
conditions must be satisfied:
1. There must be a force (F) exerted on an
object and made it move.
2. There must be a displacement (x) either
in the same or opposite direction as the
applied force.
3. There must be a component of force
along the direction of the displacement.

6. • The SI unit of Work is newton-meter (N-m)
or also known as joule (J) which is defined
as the work expended by a force of 1N
through a distance of 1m.
1 joule = 1 newton- meter
• The SI unit of work is named after James
Prescott Joule ( 1818-1889), an English
physicist who showed the quantitative
relationship of heat and work. He is one of
the outstanding physicist of the 19th
Century.

7. • The non-SI unit of Work includes
dyne-cm or erg and foot-poundal
(ft-lb)

9. Sample Problems

10. • Example:
1. If a 50 pound force is exerted on a crate at it
moves 10 feet across the floor in the direction of
the force then the work done is 50 pounds times
10 feet.
Given:
F = 50 lbs
x = 10 ft
W = ?
Formula:
W = Fx
= (50lbs) (10ft)
W = 500 ft-lbs

11. 2. How much work is done when a 50 kg block is
pushed by a horizontal force of 60 N through a
distance of 25 m?
Given:
F = 60 N
d = 25 m
W =?
Formula:
W = Fd
= (60 N) (25 m)
W = 1,500 J

12. • On the other hand, one of the most common
ways of doing work is raising a body. The work
done in raising a body against the force of
gravity is equal to the weight of the body
multiplied by the height through which the body
has been raised.
• A body of mass m kg through a height h
expressed in meters. If the body is raised with
no acceleration, then the upward force in raising
the body is equal to the weight in newton, where
W = mgh

13. • Therefore, the work done is equal to weight
multiplied by height (vertical distance).
where:
Weight = mass x acceleration due to gravity
W = mg
W = mgh
where:
m= mass of the object
h = the distance where the body was raised
g = acceleration due to gravity which is 9.8 m/

14. Examples:
1. Suppose a person who weighs 600 newtons
goes up the stairway from the ground floor to the
third floor of a building. If the distance between the
floors is 4 meters, the person raises himself
through a height of 8 meters.
Given:
m= 600 N
h= 8 m
Formula:
W= mgh
= (600 N)(9.8 m/)(8 m)
W= 47,040 J

15. 2. How much work is required to raise a load of 50
kg from the ground to the tenth floor of a building
30 meters above the ground?
Given:
m = 50 kg
h = 30 m
g = 9.8 m/
Formula:
W = mgh
= (50 kg) (9.8 m/)(30 m)
= (490 N) (30 m)
= 14,700 J

16. 3. Find the work done when a person
weighing 600 N clubs a tower 50 m high.
Given:
m = 600 N
h= 50 m
g = 9.8 m/s
Formula:
W= mgh
= (600 N)(9.8m/s) (50 m)
W = 294 000 J

17. 4. A laborer who weighs 600 newtons is to
carry 5 sacks of rice from the ground to the
second floor of a storehouse. If the distance
between floors is 3.5 meters and the weigh
of each sack is 50 kg of force, find the total
work done against gravity if the laborer
carries only one sack at a time.
Solution:
The laborer will have to make five
trips to the second floor. The force he exerts
is equal to the sum of his weight and the
weight of one sack.

18. Since the weight of each sack= 50 kg x 9.8 m/
= 490 N
Work for each trip = (600 N + 490 N) x
3.5 m
= 1,090 N x 3.5 m
= 3,815 J
Hence, the total work done = 5x 3,815 J
= 19,075 J

19. • Work can either positive or negative:
if the force has a component in the
same direction as the displacement of
the object, the force is doing positive
work. If the force has a component in
the direction opposite to the
displacement, the force does negative
work.

20. • Example:
If you pick a book off the floor and put it on
a table, for example you're doing positive
work on the book because you supplied an
upward force and the book went up. If you
pick the book up and place it gently back on
the floor, you're doing negative work
because the book is going down but you're
exerting an upward force acting against
gravity.

21. ENERGY

22. What is energy?
• Energy is defined as the property of
matter that is manifest as a capacity
to perform work such as causing
motion or the interaction of
molecules.

23. Forms of Energy
1. Chemical energy- the energy of mixture of
chemicals that can do work that happens during
chemical reaction
Ex. Food energy
2. Electrical energy- most important energy in modern
technological world. It is linked with the basic structure
of an atom.
3. Radiant energy caused by the accelerated electric
charges or magnetic fields.
4. Nuclear energy-energy release during the splitting
or fusing of atomic nuclei.
5. Solar energy- is the radiation produced by nuclear
fusion reactions deep in the sun's core.

24. 6. Light energy- an energy visible to human
eye that is radiated in moving particles.
7. Thermal energy- energy in transit that
flow flows from a substance at a higher
temperature to the substance at a low er
temperature.
8. Wind energy- energy contained in the
force of the winds blowing across the
surface of the earth.
9. Mechanical energy- is due to the
position of something or the movement of
something.

25. Mechanical Energy
• Mechanical energy is the energy that is
possessed by an object due to its motion
or due to its position. It is the energy
acquired by objects upon which work is
done.
• Mechanical Energy is divided into two
classes:
1. Potential Energy
2. Kinetic Energy

26. Potential Energy
• Potential energy ( stored energy of
position) is an energy possessed by a
body due to its position, shape or
configuration.
2 Principal Types
1. Gravitational potential energy
2. Elastic potential energy

27. Potential Energy
• Gravitational potential energy is possessed by
a body by virtue of its position, usually relative to
the ground. The gravitational potential energy of
a body is taken usually as a zero when it is at
ground level.
Example:
1. A physics book at rest on the top shelf of a
locker possesses mechanical energy due to its
vertical position above the ground.

28. 2. A barbell lifted high above a weightlifter's head.
3. A heavy block is raised by an engine to a height
of 10 meters from the ground.
The potential energy of a body of mass at a
height from the ground is equal to the work done in
rising the body from the ground to that height.
Hence, P.Egrav = mgh
where: m = mass in kg
h = height in m
g = acceleration due to gravity which
is 9.8 m/

29. • Energy and work are expressed in the
same unit since work is also the
amount of energy transferred.

30. Example
1. Find the increase in potential energy of a body
when it is raised through a height of 12 m if the
mass of the body is 40 kg.
Given:
h = 12 m
m= 40 kg
g = 9.8 m/
P.Egrav = ?
Formula & solution:
P.Egrav = mgh
= (40 kg) (9.8 m/) (12m)
= (392 N) (12m)
= 4,704 J

31. Elastic Potential Energy
• Elastic potential energy is the energy
stored in elastic materials as the result of
stretching or compressing.
• It can be stored in rubber bands, bungee
cords, trampolines, springs, an arrow drawn
into a bow, air compressor, air brakes of
trains etc.
• The amount of elastic potential energy is
such a device is related to the amount of
stretch of the device- more stretch, the more
stored energy.

34. Kinetic Energy
• Kinetic energy ( energy in motion) is the energy
associated with motion. An object may have
kinetic energy because it is moving as a whole
or because it is rotating or both.
• Kinetic energy (KE) is the energy possessed by
bodies in motion. It is equal to one-half the
product of object's mass (m) and the square of
its velocity ().
KE = m
Kinetic energy depends upon the mass of the
moving object.

35. Sample Problems

36. Problem:
1. A 55 kg man runs at a speed of 4 m/s. Find his kinetic energy.
Given:
m = 55 kg
v = 4 m/s
KE = ?
Formula:
KE = m
= ( 55 kg) (4 m/s
= ( 55 kg) (16 )
= ( 880 J)
= 440 J

37. Law of Conservation of
Energy
• The law of conservation of energy states
energy can neither be created nor
destroyed, it can only be transformed from
one form to another.
• The law of conservation of energy is one
of the basic laws of physics and therefore
governs the microscopic motion of
individual atoms in a chemical reaction.

38. Examples:
1. Water can produce electricity. Water falls from the
sky, converting potential energy to kinetic energy.
This energy is then used to rotate the turbine of a
generator to produce electricity. In this process the
potential energy of a water in a dam can be turned
into kinetic energy which can then become electric
energy.
2. When you push a book across the table, the energy
from your moving arm is transferred from your body
to the book, causing the book to move.
3. A cat sitting on the highest branch of a tree has
what is known as potential energy. If he falls off the
branch and falls to the ground, his potential energy
is now being converted into kinetic energy.

39. 4. Fingers hitting the piano keys transfer
energy from the player’s hand to the keys.
5. When a moving car hits a parked car and
causes the parked car to move, energy is
transferred from the moving car to the
parked car.

40. POWER

41. Power
Power is defined as the rate of doing work. It is thus distinct
from work and energy, with which the term is often confused.
Power bears the same relation to work as velocity near the
distance. The average power is defined by the relationship:
average power =
Power (P) is work (W) done divided by the time (t) it takes to
do the work.
Formula:
P =
W = Pt
t =

42. Power is measured in watts (W),
named in honor of the Scottish
mathematician and engineer James
Watt, who greatly inspired the steam
engine.
1 watt = 1 J/s

43. • James Watt used a horse to estimate
the value of power. He compared the
power to his steam engine with the
power of a horse. He found that the
horse can lift or pull 550-lbs weight to
a distance of one foot in one second.
One horsepower (hp) equals 746
watts.
1 hp =746 watts= 550 ft-lbs

44. • The units of power are the units of work divided
by time, which are joules/second in SI unit.
Consistent with the practice of using a new
name when a unit is added, this unit is called a
watt (W). The kilowatt, 1000 watts is also
commonly used. The basic power unit in the
British system is the ft-lb/sec. the horsepower is
derived from this units:
1 horsepower = 550ft-lb/sec
= 33, 000 ft-lb/h
kW = 1000 W
1MW= 1, 000, 000

45. When a constant a force (F) performs work (W)
on an object and moves it at constant rate, the power
developed is equal to the product of the force (F) and
velocity (v).
In equation:
P = = = F () = Fv or P = Fv
The derived formula for will be P =
and velocity will be v =
This equation reveals that a powerful machine is
both strong (big force) and fast ( big velocity). A
powerful person or machine must have a great force,
to make an object move a great distance, in a short
period of time.

46. Example:
1. An electric motor lifts an elevator that weighs 2.40 x N a
distance of 18.0 m in 30.0 s. What is the power of the
motor in watts? In kilowatts?
Given:
F = 2.40 x N
x = 18.0 m
t = 30.0 s
P = ?
Solution:
P = = =
=
= W
= kW

47. Machines

48. The Principles of
Machines

49. Machines in general may be looked
upon as devices for transforming energy.
The applications of simple machines such
as hand tools are often for the purpose of
multiplying force, that is for obtaining a
larger output force than one exerts on the
tool. However, a machine cannot supply
more output energy than it is given as input
energy. i.e. the output energy this follows the
conservation of energy principle: energy
cannot be created by the machine.

50. Machine
- Greek word “machos”-
expedient or something that makes
work easy.
-Roman word “machina”
which means “trick” or “device”.

51. A machine is device that
transfers energy from one place to
another or transforms it from one
form to another form. It is used to
increase the force, or to increase
the speed, or simply to change the
direction of forces. But it does not
change the amount of work done.

52. Machine is describe as the
complex mechanical device
powered by an engine or
electric motor and designed to
perform useful labor saving
tasks.

53. A common misconception is that
machines are used to do a task with
less work than would be needed to
do the task without the machine. In
fact, due to friction, you do more
work with a machine than without it
for the same task. No machine can
do the work on its own. Man must do
an input work on the machine so that
the machine can do the output work.

54. Input work (Wi) or the work done by
man on the machine, is usually greater
than the output work (Wo) or the work
done on the machine.
only ideal machine can transfer all
the energy so the output work equals the
input work. Real machines have friction
between moving parts, so some work is
wasted due to heat, and the output work
becomes lesser than the input work.

55. Since we know that work equals : W = Fx
then = and =
Where:
= input force = the force you exerted or
applied on a machine
= output force = the force exerted by the
machine
= input distance = displacement caused by
man
= output distance = displacement caused by
the machine.

56. The major benefit of a machine is that the
input work can be done lesser input force, but a
greater input distance.
Since, work equals force multiplied by
distance, then, large force times small distance
equals small force times large distance. It
means that no machine can increase the force
and the speed at the same time. A machine
which has the advantage of increasing force
has the disadvantage of decreasing the
distance (and the speed), and vice versa.
If the machine is a force multiplier, it
cannot be a speed multiplier and vice versa.

57. Example:
1. We need 1000 J of work to lift a 1000 N load to
a height of 1 m. if this load is pushed up on an
inclined plane (with negligible friction) that is 4
m long, it will require only 250 N to do it.
( In reality, friction between the load and the
inclined plane will make the applied force greater
than 250 N.)
Proof : = = (1000 N) (1m) = 1000 J
= = ( 250 N) (4m) = 1000 J

58. Moving heavy objects, such as a pile of
rocks, can be made much easier with
machines. Machines can be simple, like a
shovel, or more complicated, like a
bulldozer. Simple machines are usually
made up of only a few parts. They can be
combined to make a complex machine. This
chapter will look at types of simple machines
and how they can be combined to make a
more complex machine.

59. Simple machines
Simple machines are able to increase a
force when energy is added to them. This
means that they make work easier. Simple
machines can also change the direction of
the force or make things go faster. There are
different types of simple machines, including
levers, inclined planes, wedges, pulleys,
wheels and axles.

60. Complex machines
A complex machine is a machine that is
made up of more than one simple machine.
The simple machines work together to make
work easier. Cars and bicycles are examples
of complex machines. You can see some of
the different simple machines that you have
read about by looking at a bicycle.

61. A bicycle has wheels and axles
that move the bike along. The
handlebars, handbrakes and brake
pedals are all types of levers. Many
bikes also have gears that allow the
rider to change the turning force. You
can change the gears to make it easier
to ride a bike up an inclined plane. The
pedals need to be turned more but it is
easier to travel uphill.

62. Levers
A lever is a bar or rod that sits and
turns on a fixed support called a fulcrum.
Levers are good for lifting. Force is applied
to one end of the lever to move a load at the
other end. Levers can be used to increase
force or to change a small movement into a
bigger one. Examples of levers include
crowbars, see-saws, fishing rods,
wheelbarrows and a pair of scissors. With
these levers, heavy objects can be moved
much more easily.

66. There are three orders of levers,
defined by whether the fulcrum, load or
effort is in the middle. A first order lever, with
the fulcrum located in the middle, is what
you have when you use a pair of scissors or
a pair of pliers to work with something. A
second order lever, with the load located in
the middle, is what you see when you use a
pair of nutcrackers or a wheelbarrow. A third
order lever, with the effort located in the
middle, is what you see when you use a
fishing rod or a pair of tweezers or tongs
with a spring at one end.

67. Inclined planes and wedges
An inclined plane is the name for a
slope or ramp which allows large weights to
be raised to a higher level with a smaller
effort. A road winding around a mountain is
an inclined plane and so is a ramp. A ramp
is longer than the height of a step but it is
much easier to push a wheelbarrow along
the ramp than to pull it up a step. Another
example of an inclined plane is a wedge.

71. A wedge is an inclined plane that
pushes objects apart. An axe, knife and a
chisel are wedges because their blades are
sloped like an inclined plane. These simple
machines multiply the effort that you apply
and make it easier to cut things. A saw is
another type of wedge. Each of the teeth
along the blade acts like a separate wedge
so much less effort or force is needed to cut
the wood.

75. Wheels, axles and gears
Wheels are found in all sorts of machines,
particularly in most forms of transport. A wheel is
actually considered a type of lever that moves in a
complete circle. The fulcrum is at the centre of the
wheel. A wheel needs an axle to hold it so that it
can turn.
An axle is a small wheel at the centre of
larger wheel. The axle turns with the larger wheel
and can move a load a great distance. You can
see an axle when you look at a bicycle. The axle is
the smaller wheel at the centre of the larger
wheels.

76. Gears are also wheels. Gear
wheels have teeth around the edge that
fit into teeth on other gears or wheels.
These toothed wheels turn other
toothed wheels. Gears are used to
make things turn faster or slower and to
increase the turning force. You can find
gears in cars, bikes, windmills and
various toys with motors.

80. Pulleys
Pulleys also use wheels to work. A pulley is a
simple machine which is made up of a grooved
wheel, an axle and a rope that can be moved
freely over the wheel. Pulleys are used to make
lifting loads easier. A pulley works by pulling
downwards on a rope that is stretched over a
wheel. The load is then lifted upwards. Two or
more pulleys can be used together to make it
easier to lift even heavier loads. Examples of
machines with pulleys include washing machines,
clothes dryers and cranes.