Downloaded 13 times
Uploaded bymjurkiewicz
Work and Energy
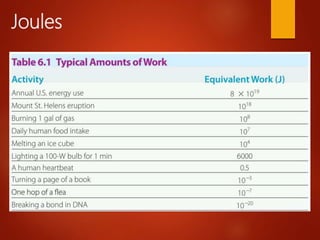
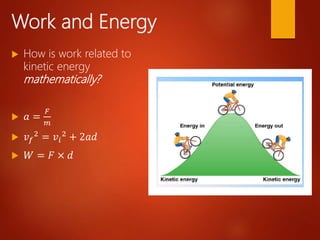
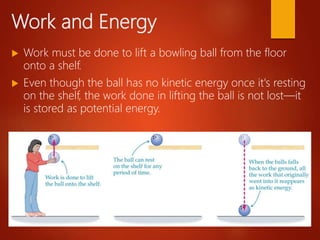
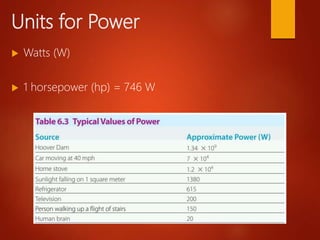
This document discusses work, energy, and power. It defines work as force applied over a distance, and explains that work is calculated as force times distance. It also discusses how work can be positive, negative, or zero depending on the direction of force relative to motion. The document then explains how work relates to changes in kinetic energy, and introduces the kinetic energy and gravitational potential energy formulas. It emphasizes that the total work done on an object equals the change in its kinetic energy. Finally, it defines power as the rate at which work is done.
More Related Content
Work and Energy
- 1.
- 2. Work Occurs whenforce is applied to an object and the object moves in the direction of the force Work = force × distance 𝑊 = 𝐹𝑑 Force (N) × distance (m) = N×m (called a “Joule,” J)
- 3.
- 4. Work No workis being done when holding a heavy object, like a suitcase However, you feel tired because your muscle cells are doing work individually
- 5. Work at anAngle Work is easily calculated when the force and displacement are in the same direction, but how is work calculated when the force is at an angle to the displacement?
- 6. Work at anAngle Only the component of the force in the direction of the displacement does work. In the image, the component of force in the direction of displacement is F cosθ
- 7. Work Work canbe positive, negative, or zero Work is positive if the force has a component in the direction of motion (Figure a) Work is zero if the force has no component in the direction of motion (Figure b) Work is negative if the force has a component opposite the direction of motion (Figure c)
- 8. Work When morethan one force acts on an object, the total work is the sum of the work done by each force separately Wtotal = W1 + W2 + W3 + …
- 9. Work and Energy When work is done on an object, the object’s energy changes What kind of energy is increasing in these examples? Pushing a shopping cart Climbing a mountain
- 10. Review of EnergyTypes Kinetic energy: energy of motion Potential energy: stored energy (position or condition) Types of potential energy: Gravitational potential Elastic potential Chemical potential
- 11. Work and Energy How is work related to kinetic energy mathematically? 𝑎 = 𝐹 𝑚 𝑣𝑓 2 = 𝑣𝑖 2 + 2𝑎𝑑 𝑊 = 𝐹 × 𝑑
- 12. Kinetic Energy Formula 𝐾𝐸 = 1 2 𝑚𝑣2 Units: Joules (J)
- 13. Practice Problem Calculatethe kinetic energy of a truck traveling at 6.0 m/s. The truck has a mass of 3900 kg. What would happen to the amount of kinetic energy if the truck doubled its speed to 12 m/s?
- 14. Work and Energy The total work done on an object equals the change in that object’s kinetic energy. 𝑊𝑡𝑜𝑡𝑎𝑙 = ∆𝐾𝐸 𝑊𝑡𝑜𝑡𝑎𝑙 = 1 2 𝑚𝑣 𝑓 2 − 1 2 𝑚𝑣𝑖 2 Example Problem: How much work is required for a 74-kg sprinter to accelerate from rest to a speed of 2.2 m/s? Is this work positive or negative?
- 15. Work and Energy Work must be done to lift a bowling ball from the floor onto a shelf. Even though the ball has no kinetic energy once it's resting on the shelf, the work done in lifting the ball is not lost—it is stored as potential energy.
- 16. Work and PotentialEnergy Potential energy (PE) is stored for later Gravitational potential energy is stored in an object that is at some height above the ground and has the potential to fall Lifting a mass (m) from the ground to a height (h) requires a force (ma or mg). Thus, the work done and potential energy acquired equals FORCE x DISTANCE, or… 𝑊 = 𝑚𝑔ℎ
- 17. Practice Problem Findthe gravitational potential energy of a 65-kg person standing on a diving board that is 3.0 meters high.
- 18. Conservation of Energy Law of Conservation of Energy states that energy can be transformed from one form to another but never lost or gained This concept is essential for solving many physics problems NOTE: objects moving downward through the same vertical distance but following different paths will have the same final speed
- 19. Practice Problem Awoman drops her keys from a height of 1.2 meters. If the keys have a mass of 0.12 kg, what is their final speed when they hit the ground?
- 21. Power Doing thesame amount of work in a shorter amount of time takes more effort. Scientists refer to this effort as POWER. 𝑃 = 𝑊 𝑡 Units: 𝐽 𝑠 or watts (W)
- 22. Power To bepowerful, an engine must produce a substantial amount of work in a relatively short time. Similarly, you produce more power when running up a flight of stairs than when walking up.
- 23. Units for Power Watts (W) 1 horsepower (hp) = 746 W