Downloaded 1,404 times
Uploaded byFazirah Abdul Ghafar
Calculating truss forces
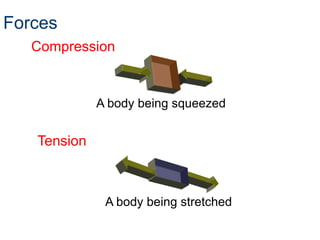
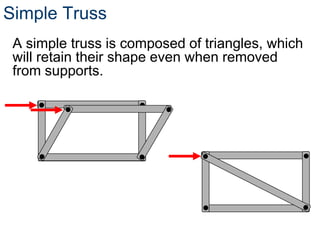
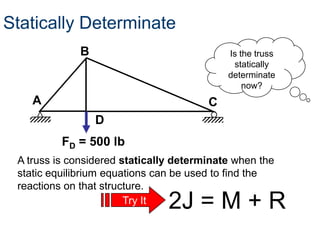
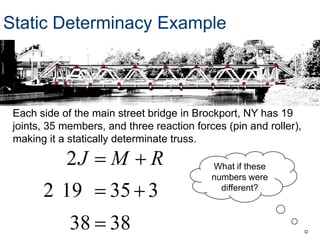
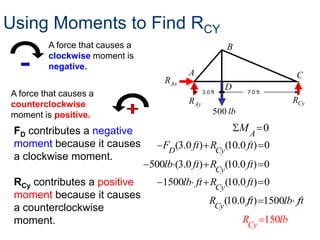
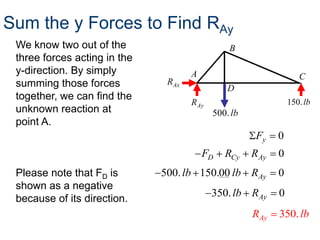
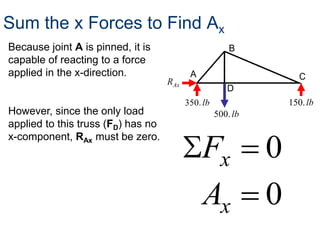
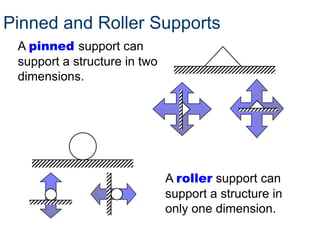
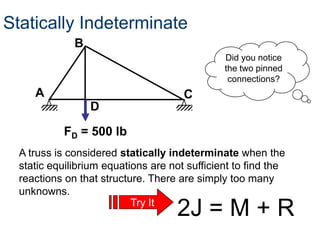
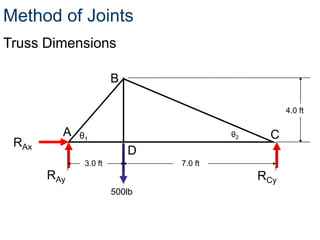
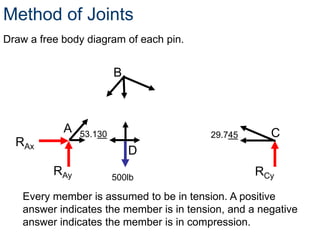
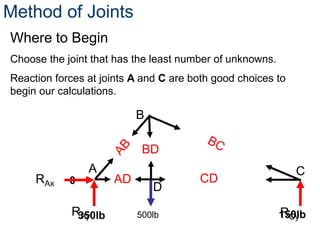
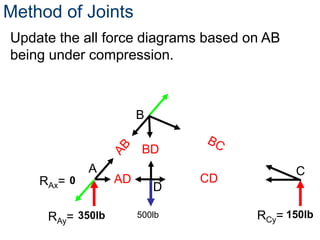
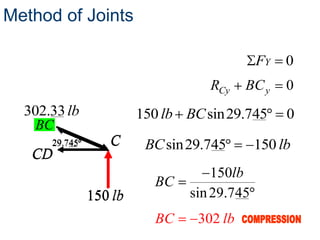
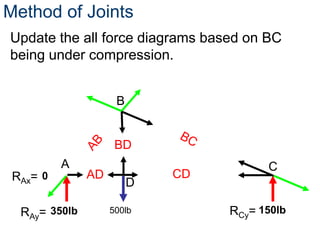
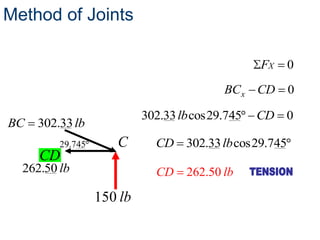
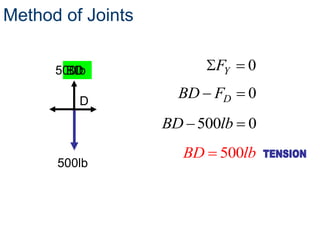
- A truss is a structure composed of slender members joined at their endpoints. Trusses use triangular shapes that retain their form even when supports are removed. - To solve for forces in a truss, assumptions are made that members are straight, loads apply at joints, joints are frictionless pins, members have no weight, and members experience only tension or compression. - The method of joints is used to solve each joint by summing forces and moments. Free body diagrams are drawn and updated as member forces are solved sequentially. 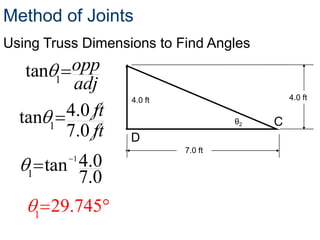- This process begins at a simply supported joint and uses trigonometry and equilibrium equations to calculate member forces throughout the truss.
More Related Content
Similar to Calculating truss forces
Calculating truss forces
- 1.
- 2. Forces Compression A body being squeezed Tension A body being stretched
- 3. Truss A trussis composed of slender members joined together at their end points. – They are usually joined by welds or gusset plates.
- 4. Simple Truss Asimple truss is composed of triangles, which will retain their shape even when removed from supports.
- 5. Pinned and RollerSupports A pinned support can support a structure in two dimensions. A roller support can support a structure in only one dimension.
- 6. Solving Truss Forces Assumptions: All members are perfectly straight. All loads are applied at the joints. All joints are pinned and frictionless. Each member has no weight. Members can only experience tension or compression forces. What risks might these assumptions pose if we were designing an actual bridge?
- 7. Static Determinacy Astatically determinate structure is one that can be mathematically solved. 2J = M + R J = Number of Joints M = Number of Members R = Number of Reactions
- 8. Statically Indeterminate B Did you notice the two pinned connections? A C D FD = 500 lb A truss is considered statically indeterminate when the static equilibrium equations are not sufficient to find the reactions on that structure. There are simply too many unknowns. Try It 2J = M + R
- 9. Statically Determinate B Is the truss statically determinate now? A C D FD = 500 lb A truss is considered statically determinate when the static equilibrium equations can be used to find the reactions on that structure. Try It 2J = M + R
- 10. Static Determinacy Example Each side of the main street bridge in Brockport, NY has 19 joints, 35 members, and three reaction forces (pin and roller), making it a statically determinate truss. 2J M R What if these numbers were 2 19 35 3 different? 38 38
- 11. Equilibrium Equations M 0 The sum of the moments about a given point is zero.
- 12. Equilibrium Equations Fx 0 The sum of the forces in the x-direction is zero. Do you remember the Cartesian coordinate system? A vector that acts to the right is positive, and a vector that acts to the left is negative.
- 13. Equilibrium Equations Fy 0 The sum of the forces in the y-direction is zero. A vector that acts up is positive, and a vector that acts down is negative.
- 14. Using Moments toFind RCY A force that causes a B clockwise moment is negative. A C RAx D A force that causes a 3.0 ft 7.0 ft counterclockwise R Ay RCy moment is positive. 500 lb FD contributes a negative MA 0 moment because it causes FD(3.0 ft) RCy(10.0 ft) 0 a clockwise moment. 500lb (3.0 ft) RCy(10.0 ft) 0 RCy contributes a positive 1500lb ft RCy(10.0 ft) 0 moment because it causes RCy (10.0 ft) 1500lb ft a counterclockwise moment. RCy 150lb
- 15. Sum the yForces to Find RAy We know two out of the B three forces acting in the y-direction. By simply A C summing those forces RAx D together, we can find the 150. lb R Ay unknown reaction at 500. lb point A. Fy 0 FD RCy RAy 0 Please note that FD is 500. lb 150.00 lb RAy 0 shown as a negative 350. lb RAy 0 because of its direction. RAy 350. lb
- 16. Sum the xForces to Find Ax Because joint A is pinned, it is B capable of reacting to a force applied in the x-direction. A C RAx D 350. lb 150. lb However, since the only load 500. lb applied to this truss (FD) has no x-component, RAx must be zero. Fx 0 Ax 0
- 17. Method of Joints Use cosine and sine to determine x and y vector components. Assume all members to be in tension. A positive answer will mean the member is in tension, and a negative number will mean the B member is in compression. As forces are solved, update free body diagrams. Use correct magnitude and sense for subsequent joint free body diagrams.
- 18. Method of Joints TrussDimensions B 4.0 ft A θ1 θ2 C RAx D 3.0 ft 7.0 ft RAy RCy 500lb
- 19. Method of Joints UsingTruss Dimensions to Find Angles B tan opp 1 adj 4.0 ft 4.0 ft A θ1 tan 4.0 ft θ 2 C 1 D 3.0 ft 3.0 ft 7.0 ft tan 4.0 1 1 3.0 1 53.130
- 20. Method of Joints UsingTruss Dimensions to Find Angles tan 1 opp B adj 4.0 ft 4.0 ft 4.0 ft tan 1 A θ θ2 C 7.0 ft 1 D 3.0 ft 7.0 ft tan 4.0 1 1 7.0 1 29.745
- 21. Method of Joints Drawa free body diagram of each pin. B A 53.130 29.745 C RAx D RAy 500lb RCy Every member is assumed to be in tension. A positive answer indicates the member is in tension, and a negative answer indicates the member is in compression.
- 22. Method of Joints Whereto Begin Choose the joint that has the least number of unknowns. Reaction forces at joints A and C are both good choices to begin our calculations. B BD A C RAx 0 AD CD D RAy 350lb 500lb RCy 150lb
- 23. Method of Joints FY 0 RAy AB y 0 437.50 lb 350lb AB sin 53.130 0 AB AB sin 53.130 350lb A 53.130 AD 350lb AB 350 lb sin 53.130 AB 438 lb
- 24. Method of Joints Updatethe all force diagrams based on AB being under compression. B BD A C RAx= 0 AD CD D RAy= 350lb 500lb RCy= 150lb
- 25. Method of Joints FX 0 ABx AD 0 437.50 lb cos53.130 AD 0 AB 437.50 lb AD 437.50 lb cos53.130 A 53.130 AD AD 262.50 lb 262.50 lb 350 lb
- 26. Method of Joints FY 0 RCy BC y 0 302.33 lb 150 lb BC sin 29.745 0 BC 29.745 C BC sin 29.745 150 lb CD 150lb BC 150 lb sin 29.745 BC 302 lb
- 27. Method of Joints Updatethe all force diagrams based on BC being under compression. B BD A C RAx= 0 AD CD D RAy= 350lb 500lb RCy= 150lb
- 28. Method of Joints FX 0 BCx CD 0 302.33 lb cos29.745 CD 0 BC 302.33 lb 29.745 C CD 302.33 lb cos29.745 CD 262.50 lb CD 262.50 lb 150 lb
- 29. Method of Joints 500lb BD FY 0 D BD FD 0 BD 500lb 0 BD 500lb 500lb