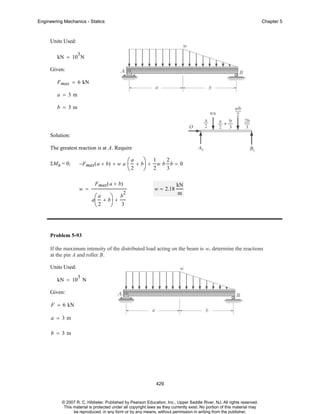
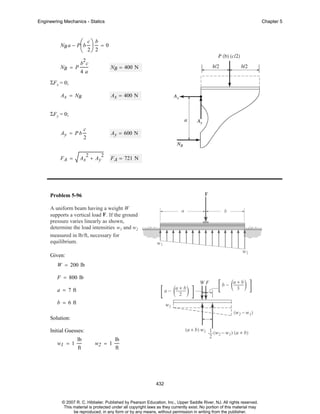
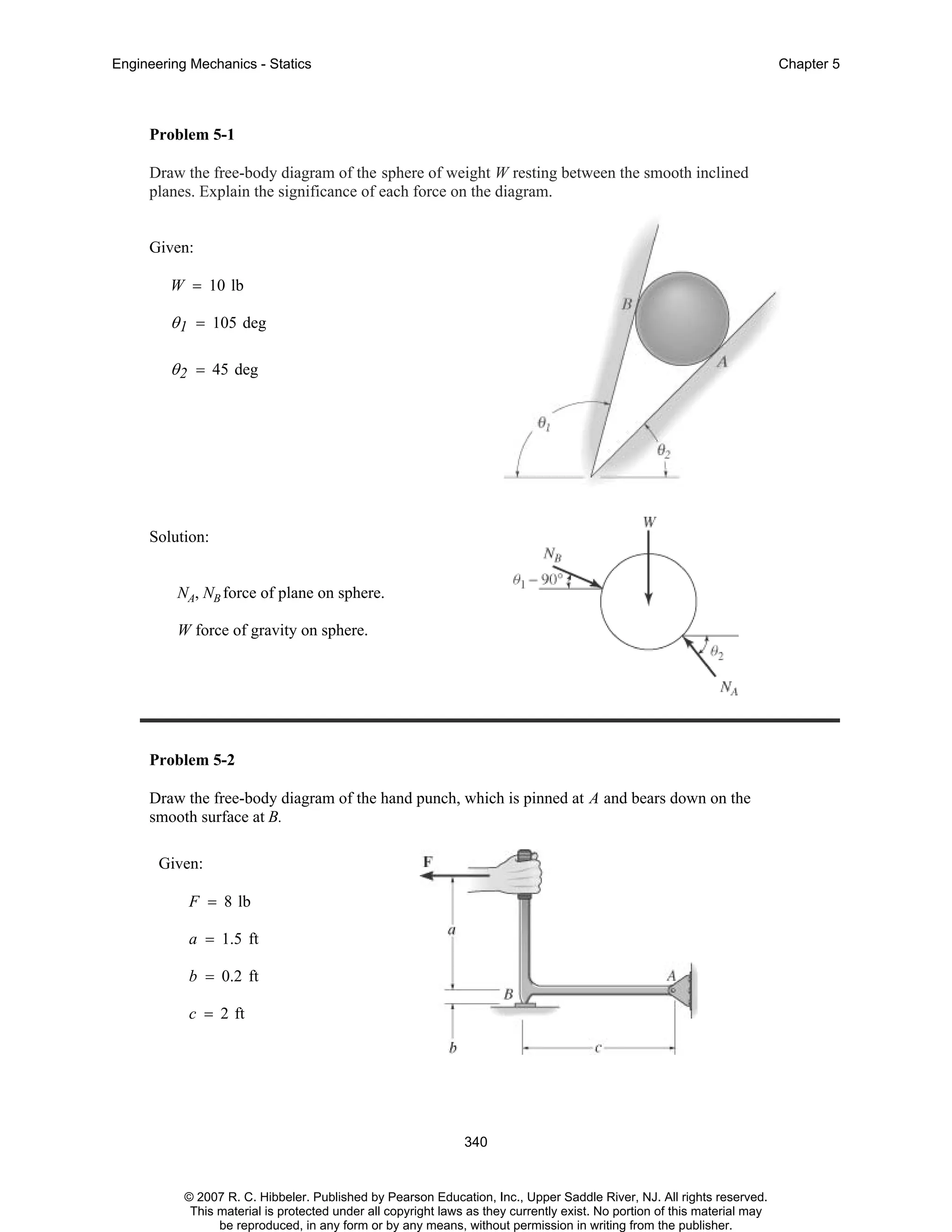
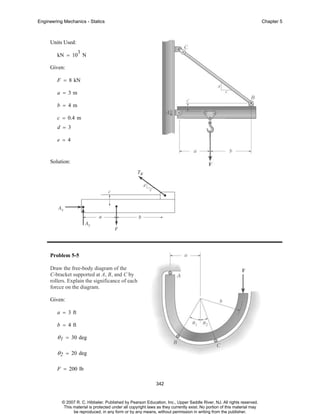
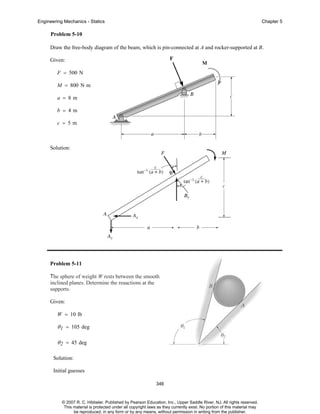
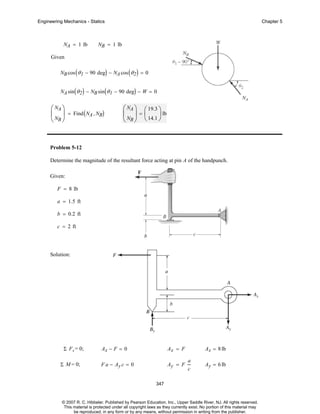
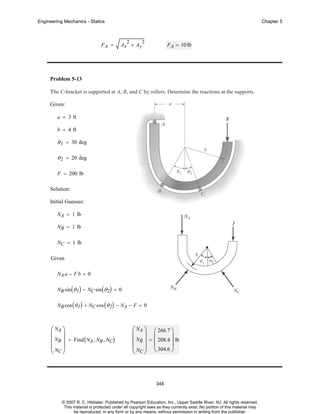
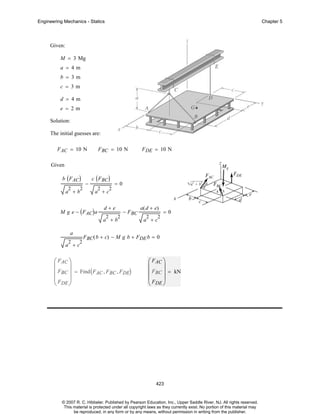
The document is a chapter from an engineering mechanics textbook covering statics. It provides 11 example problems involving drawing free body diagrams to represent physical systems. The problems include spheres, beams, cranes, rods, and other objects, and require identifying the relevant forces and calculating reactions. Solutions are provided for each problem, with diagrams and step-by-step working. The chapter demonstrates how to set up and solve static equilibrium problems using free body diagrams.











































































![Engineering Mechanics - Statics
Chapter 5
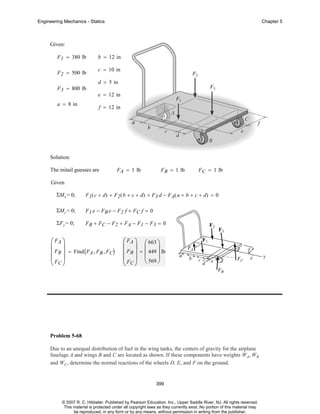
Solution:
Initial Guesses:
Az = 1 lb
B z = 2 lb
Cz = 31 lb
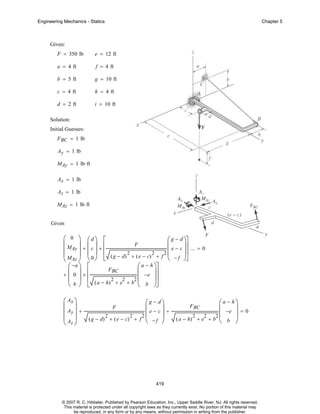
Given
ΣMy = 0; B z r cos ( θ 1 ) − Cz r cos ( θ 1 ) − F sin ( θ 3 ) c = 0
[1]
ΣMx = 0; −B z r sin ( θ 1 ) − Cz r sin ( θ 1 ) + Az r − F cos ( θ 3 ) c = 0
[2]
ΣF z = 0; Az + Bz + Cz = W
[3]
Solving Eqs.[1], [2] and [3] yields:
⎛ Az ⎞
⎜ ⎟
⎜ Bz ⎟ = Find ( Az , Bz , Cz)
⎜C ⎟
⎝ z⎠
⎛ Az ⎞ ⎛ 1600 ⎞
⎜ ⎟ ⎜
⎟
⎜ Bz ⎟ = ⎜ 1167 ⎟ lb
⎜ C ⎟ ⎝ 734 ⎠
⎝ z⎠
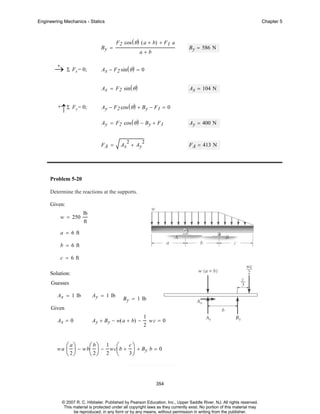
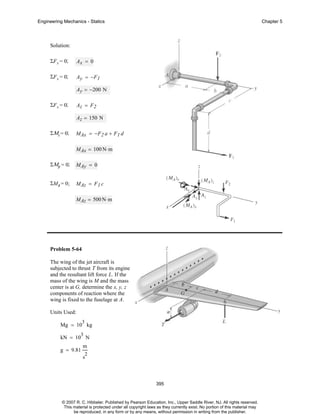
Problem 5-91
The shaft assembly is supported by two
smooth journal bearings A and B and a
short link DC. If a couple moment is
applied to the shaft as shown, determine
the components of force reaction at the
bearings and the force in the link. The
link lies in a plane parallel to the y-z plane
and the bearings are properly aligned on
the shaft.
Units Used:
3
kN = 10 N
Given:
M = 250 N⋅ m
a = 400 mm
b = 300 mm
c = 250 mm
d = 120 mm
θ = 30 deg
427
© 2007 R. C. Hibbeler. Published by Pearson Education, Inc., Upper Saddle River, NJ. All rights reserved.
This material is protected under all copyright laws as they currently exist. No portion of this material may
be reproduced, in any form or by any means, without permission in writing from the publisher.](https://image.slidesharecdn.com/hibbelerchapter5-131111222428-phpapp01/85/Hibbeler-chapter5-88-320.jpg)