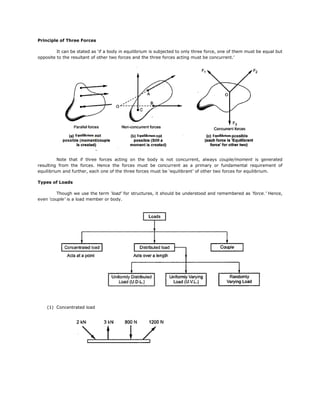
Equilibrium is the state of rest of a particle or body where the net force and net torque are zero. For a body to be in static equilibrium, the sum of the forces in the x and y directions and the sum of moments must equal zero. There are various types of loads that can act on structures including concentrated loads, uniformly distributed loads, and uniformly varying loads. Equilibrium problems of concurrent coplanar forces can be solved using the principle of two forces or three forces. Examples are provided to demonstrate solving for tensions, reactions, and other unknown forces in equilibrium problems.

1. EQUILIBRIUM
Equilibrium is the state of a particle or a body in which the body (particle) remains at rest. It can be said
that to be in static equilibrium also.
A system in static equilibrium or at rest should not have any kind of motion or movement. i.e. resultant
force as well as resulting moment of the system must be zero. Hence analytical or mathematical conditions of
equilibrium for general force system can be given as:
∑ Fx = 0
∑ Fy = 0
∑ Mo = 0
Principle of Equilibrium
Two forces principle can stated as ‘if a body acted upon by only two forces, these forces must be equal in
magnitude, opposite direction and collinear.

2. Principle of Three Forces
It can be stated as ‘if a body in equilibrium is subjected to only three force, one of them must be equal but
opposite to the resultant of other two forces and the three forces acting must be concurrent.’
Note that if three forces acting on the body is not concurrent, always couple/moment is generated
resulting from the forces. Hence the forces must be concurrent as a primary or fundamental requirement of
equilibrium and further, each one of the three forces must be ‘equilibrant’ of other two forces for equilibrium.
Types of Loads
Though we use the term ‘load’ for structures, it should be understood and remembered as ‘force.’ Hence,
even ‘couple’ is a load member or body.
(1) Concentrated load

3. (2) Uniformly distributed loads
(3) Uniformly varying loads
Equivalent Point Load

4. EQUILIBRIUM OF CONCURRENT COPLANAR FORCES
Example:
A boom AC hinged at A supports a 400 N load as shown. Find the force in cable BC, which is attached to
the wall at B. Neglect self weight of boom.
Solution:
FBD:
[∑ F x = 0] → +
−T cos 30 o + F cos 45 o = 0
 cos 30 o 
F = T
 cos 45 o 

  eq. 1
[∑ F
y ]
=0 ↑+
T sin 30 o + F sin 45o − 400N = 0
eq. 2
Substititute eq. 1 to eq. 2:
 cos 30o 
T sin 30o + T
 cos 45o
 sin 45o − 400N = 0

 
T = 292.82 N
F = 358.63 N

5. Example:
A string supported at A and B carries a load of 20 kN at C and a load W at D as shown. Find the value of
W so that CD remains horizontal. Also find the tension in string segments AC, CD and DB.
Solution:
FBD:
Solving for T1 and T2 (Using FBD A)
[∑ F
y ]
=0 ↑+
T1 sin 30 o − 20 kN = 0
T1 = 40 kN
[∑ F
x = 0] → +
−T1 cos 30 o + T2 = 0
T2 = 34.64 kN
Solving for T3 and W(Using FBD B)
[∑ F
x = 0] → +
T3 cos 60 o − T2 = 0
T3 = 69.28 kN

6. [∑ Fy ]
=0 ↑+
T3 sin 60 o − W = 0
W = 60 kN
ASSIGNMENT:
1. A mass of 45 kg is suspended by a rope from ceiling. The mass is pulled by a horizontal force until the
rope makes an angle of 70o with the ceiling. Find the horizontal force and tension in the rope.
Ans. T = 469.78 N, F=160.67 N
2. Bar AC 10 m long supports a load of 6000 N as shown. The cable BC is horizontal and 5 m long.
Determine forces in the cable and the bar.
Ans. F = 6928.2 N, T = 3464.1 N
3. A sphere of weight W is kept at rest in V-groove as shown in the figure. If W = 750 N, find reactions at
point of contact.
Ans. R1 = 272.87 N @ 40 deg; R2 = 611.22 N @ 70 deg

7. 4. A 40 kg cylinder is held in position on an inclined plane by means of a wire AB as shown in figure.
Determine reaction at surface of inclined plane and tension in the wire.
Ans. T = 319.5 N, R = 436.1 N @ 45 deg
5. A 12 kg uniform rod AB is held in equilibrium as shown by two strings OA and OB. Find the tension in the
strings.
Ans. T1 = 76.84 N, T2 = 52.6 N
6. Pipes A and B of 500 N and 1.25 kN weight are placed in a channel as shown. If the diameters of pipes are
150 mm and 270 mm respectively, find the force at each point of contact. Neglect friction.
Ans. 602.2 N, 335.7 N, 387.67 N @ 30 deg, 1556.17 N

8. 7. A 50 N uniform disc is pin connected to a light bar AB as shown, neglecting friction, determine the force in
bar AB and reactive force at the ground.
Ans. 115.47 N, 107.74 N
8. A 200 kg roller of 400 mm diameter is just to be pulled over a curb of 100 mm height as shown. Applying
force P. Compute force P and reactions at points of contact neglecting friction.
Ans. 2265.5 N, 1132.8 N
9. Rigid hook in the ceiling ‘O’ is known to offer resistance of 70 N against pulling. Determine masses A and
B which can be supported as shown, neglecting friction at pulleys. Assume cords to be inextensible.
Ans. 5.1kg and 5.8 kg

9. 10. Three homogeneous rollers A, B and C are placed in a trench as shown in the figure and have weights 300
N, 300 N and 600 N respectively. If their diameters are 800 mm, 800 mm and 1200 mm respectively,
determine the reactions at all points of contact.
Ans. 61.23 N, 306.19 N, 290.43 N, 153.09 N, 1095.24 N, 631.58 N
11. A uniform rod AB, 1.2 m long is held in the equilibrium position by a cord OA as shown. Determine the
length of cord.
Ans. 1.59 m
Reference:
Engineering Mechanics by SP Nitsure © 2006 Technical Publications Pune
Engineering Mechanics by Dr. IS Gujral © 2008 Laxmi Publications (P) Ltd.